基于循环神经网络的微地震数据降噪方法

李盼池, 石 彤, 李学贵

(东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318)

微地震是在开采井附近的岩体因应力场变化导致岩石破裂引起的微小地震事件, 微地震事件监测中检波器收集的微地震信号因易受周围环境的影响常含有大量噪声, 而含噪微地震数据会导致微地震信号识别困难, 影响微地震后续研究的准确性及可靠性. 因此, 进行微地震监测首先要对微地震数据进行降噪处理.

针对检波器采集到的微地震信号存在噪声的问题, 目前已有许多处理方法. 刁瑞等[1]采用负熵作为目标函数, 通过引入粒子群优化算法提高求解效率, 利用互相关系数处理盲源分离的不确定性问题, 有效实现了微地震数据降噪； 慕阳等[2]在实验中采用提取最优小波基, 确定分解层数及对分解信号设置合适阀值等步骤消除部分噪声, 实现了提高微地震信号信噪比的目的； 王亚娟等[3]提出了将含噪数据进行集成经验模态分解, 计算不同频率的本征模态函数(intrinsic modal function, IMF)样本熵, 设置样本熵阈值提取符合微震信号特征的IMF分量并对其进行信号重构, 从而抑制随机噪声; 弓震等[4]提出了通过学习训练大量微震资料, 构建可最大化稀疏表示微地震数据的超完备字典, 利用微地震信号与噪声在训练字典下的差异, 分离有效信号与噪声, 最终达到降噪的目的; 王飞等[5]提出了将同步压缩小波变换技术与自适应阈值处理技术相结合的方法对微地震数据实施降噪处理, 大幅度提高了微地震事件的信噪比; 邵婕等[6]首先利用正交匹配追踪算法计算多分量数据的稀疏表示, 然后在根据信号特征选择稀疏变换矩阵的同时根据噪声方差选择恰当阈值, 最后通过迭代, 重构误差直至其小于设定阈值, 从而实现微地震数据降噪; 刘利强[7]提出了首先获得极小、 极大值包络线, 然后将原始信号分解为多个满足条件的信号序列, 最后根据信号特征选取高信噪比的信号序列重构信号的方法实现微地震数据降噪.

普通循环神经网络(recurrent neural network, RNN)训练过程中易出现梯度消失与梯度爆炸的问题, 为解决这类问题, Hochreiter等[8]提出了长短时记忆单元(long short-term memory, LSTM)方法. 近年来, 随着深度学习研究的不断发展, 其已广泛应用于信号降噪等问题中. 许滔滔等[9]提出了一种基于LSTM的循环神经网络, 将其用于对大地电磁工频干扰压制, 首先构建基于LSTM循环神经网络模型, 然后将含噪数据及工频噪声分别作为模型的输入与输出, 最后获得输入与输出的差值作为降噪后的真实信号, 该方法取得了较好的降噪效果; Shen等[10]在引力波信号噪声压制中使用了基于LSTM的循环神经网络降噪模型, 利用该模型能有效去除随机噪声, 且降噪效果比传统方法优越. 此外, 还有利用LSTM的变体门控循环单元(gated recurrent unit, GRU)构建网络模型进行降噪的方法[11]. 周泽南[12]将卷积神经网络与GRU相结合, 并将其作为后续构建循环神经网络的重要单元, 与基于LSTM的循环神经网络及传统滤波方法相比, 该方法在去除InSAR图像的相位噪声方面效果明显.

在目前的微地震数据降噪方法中, 利用深度学习技术降噪的方法较少, 且传统方法均存在一些缺点, 如小波降噪中若支集长度太大则不利于实时性, 需要精准调参的问题等. 针对微地震信号的时序特性以及传统方法存在的不足, 本文构建深度双向门控循环单元循环神经网络(deep bidirectional gated recurrent unit recurrent neural network, DBGRU-RNN), 并将其应用于微地震数据降噪. 实验结果验证了DBGRU-RNN在微地震信号降噪中应用的可行性.

1 循环神经网络概述

1.1 循环神经网络

循环神经网络是一种特殊的神经网络结构, 表现为RNN会对之前时刻的信息进行记忆并应用于当前输出的计算中, 即隐藏层之间的节点有连接, 并且当前时刻隐藏层的输入不仅包括当前时刻的输入还包括上一时刻隐藏层的输出[13]. 其网络结构[14]如图1所示. 输入输出关系表示为

图1 循环神经网络结构Fig.1 Recurrent neural network structure

其中t-1,t,t+1为时间序列,x为当前输入样本,s0为初始记忆,st为输入样本在时间t处的记忆,W为前一时刻隐藏层输出的权重,U为当前时刻输入样本的权重,V为输出的样本权重,f和g为激活函数.

RNN在每步输入、 输出、 隐状态的连接中均共享参数, 这种共享机制可显著降低模型复杂度, 缩短训练时长, 还能保持较高的精度. 因此, RNN在含有时序数据的任务中有较强优势.

1.2 门控循环单元

普通RNN训练时, 经常会出现梯度消失和梯度爆炸的问题, 因此文献[15]提出了LSTM解决该问题, 其在普通RNN单元的基础上, 增加了3个可以使信息选择式通过的门控制信息的量, 从而使梯度值保持稳定, 便于训练, 但由于加入了门控机制而导致计算复杂度增高. GRU是LSTM的一种变体, 因此, 其使用门控机制学习长期依赖关系的基本思想与LSTM一致. 与LSTM相比, GRU的结构简单, 计算复杂度低, 且没有LSTM网络中内部状态和外部状态的划分, 而是通过直接在当前网络的状态ht和上一时刻网络的状态ht-1之间添加一个线性的依赖关系, 解决梯度消失和梯度爆炸的问题.其基本单元结构[16]如图2所示.

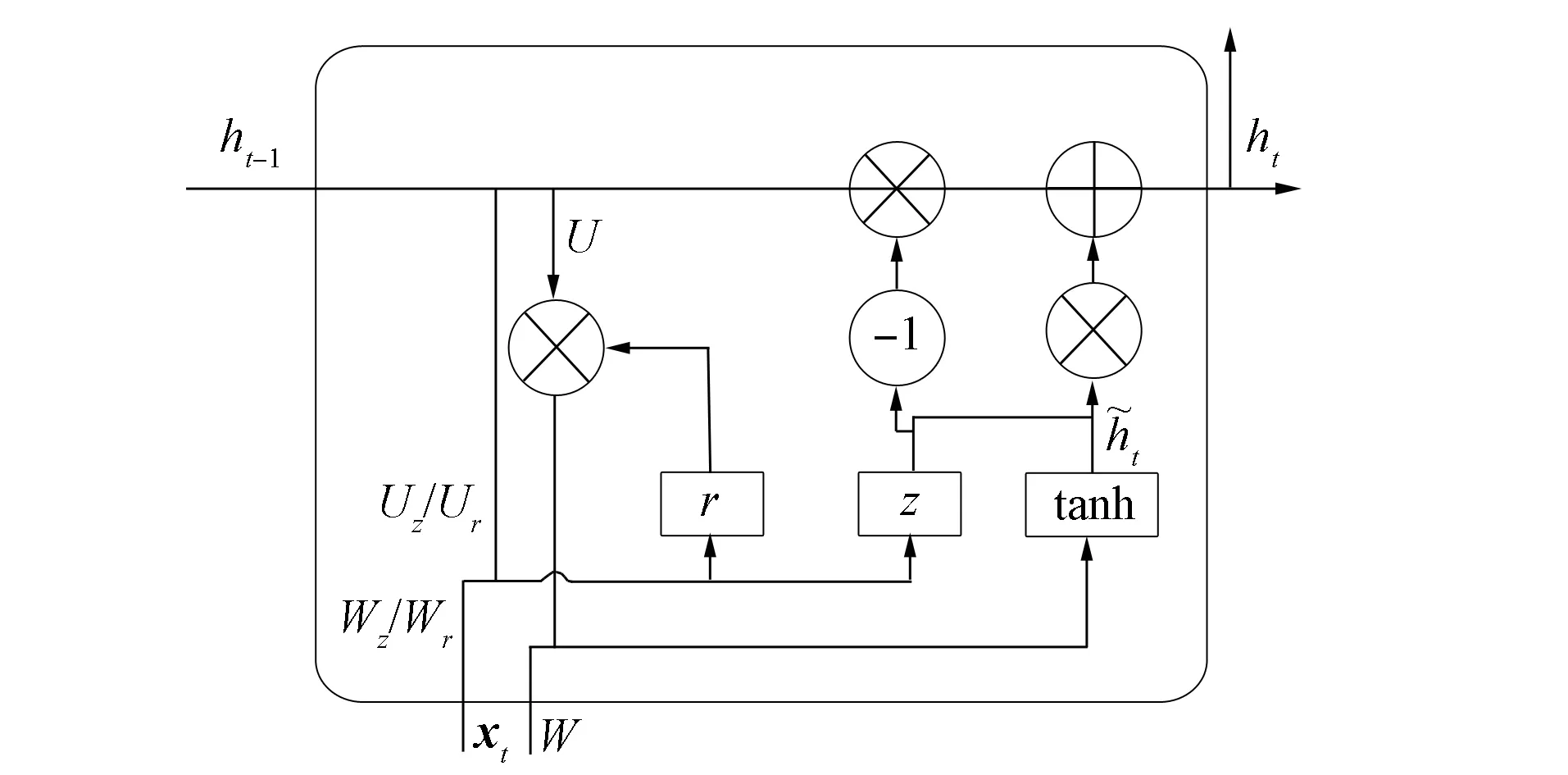
图2 单个GRU单元基本结构Fig.2 Basic structure of single GRU unit

在经典的GRU模型中, 计算过程[17]分为如下四步：

步骤1) 更新门帮助模型决定前一时刻和当前时刻的信息传递量, 其计算公式为

z=σ(Wzxt+Uzht-1+bz);

(2)

步骤2) 重置门决定前一时刻的信息遗忘量, 其计算公式为

r=σ(Wrxt+Urht-1+br)；

(3)

步骤3) 新的记忆内容使用重置门储存过去相关的信息, 其计算公式为

(4)

步骤4) 最后保留当前单元的信息并传递到下一个单元中, 其计算公式为

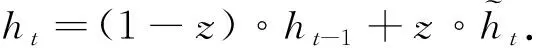
(5)

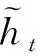
与LSTM相比, GRU的计算公式简单, 在具有同等水平数据计算上, 可大幅度提高计算效率. 理论上, 增加循环神经网络的深度及设置复杂的网络结构可增强循环神经网络的能力. 因此, 本文在增加网络层数的同时还结合了双向网络结构, 建立了DBGRU-RNN模型, 与单向GRU相比, 其某时刻的输出不仅与前一时刻的隐状态有关, 同时还与后一时刻的隐状态有关, 因此该模型能利用时序数据的上下文信息进行建模, 获得比单向GRU更准确的结果[18].

2 基于DBGRU-RNN的微地震降噪方法

本文构建网络模型时首先考虑到循环神经网络具有强大的处理序列数据的能力, 且微地震数据为一维序列数据, 提出将循环神经网络用于微地震数据降噪处理中； 其次考虑到普通循环神经网络易出现梯度消失等问题, 本文将传统循环单元替换为门控循环单元； 再次考虑到与单向循环神经网络相比, 双向循环神经网络某时刻的输出不仅与前一时刻的隐层状态有关, 同时还与后一时刻的隐层状态有关, 因此双向循环神经网络模型能充分利用时序数据的上下文信息进行建模, 获得比单向循环神经网络更准确的结果； 最后考虑到增加神经网络的深度可增加网络模型的容错能力, 提高网络模型的鲁棒性. 因此, 本文选择深度双向门控循环单元循环神经网络用于微地震数据降噪.

2.1 DBGRU-RNN模型

本文构建的DBGRU-RNN模型如图3所示, 包括3个GRU隐藏层, 由下至上分别为输入层、 GRU隐藏层和输出层. 隐藏层中实线表示前向层, 虚线表示反向层. 其中, 3个GRU隐藏层为整个网络模型的核心部分.

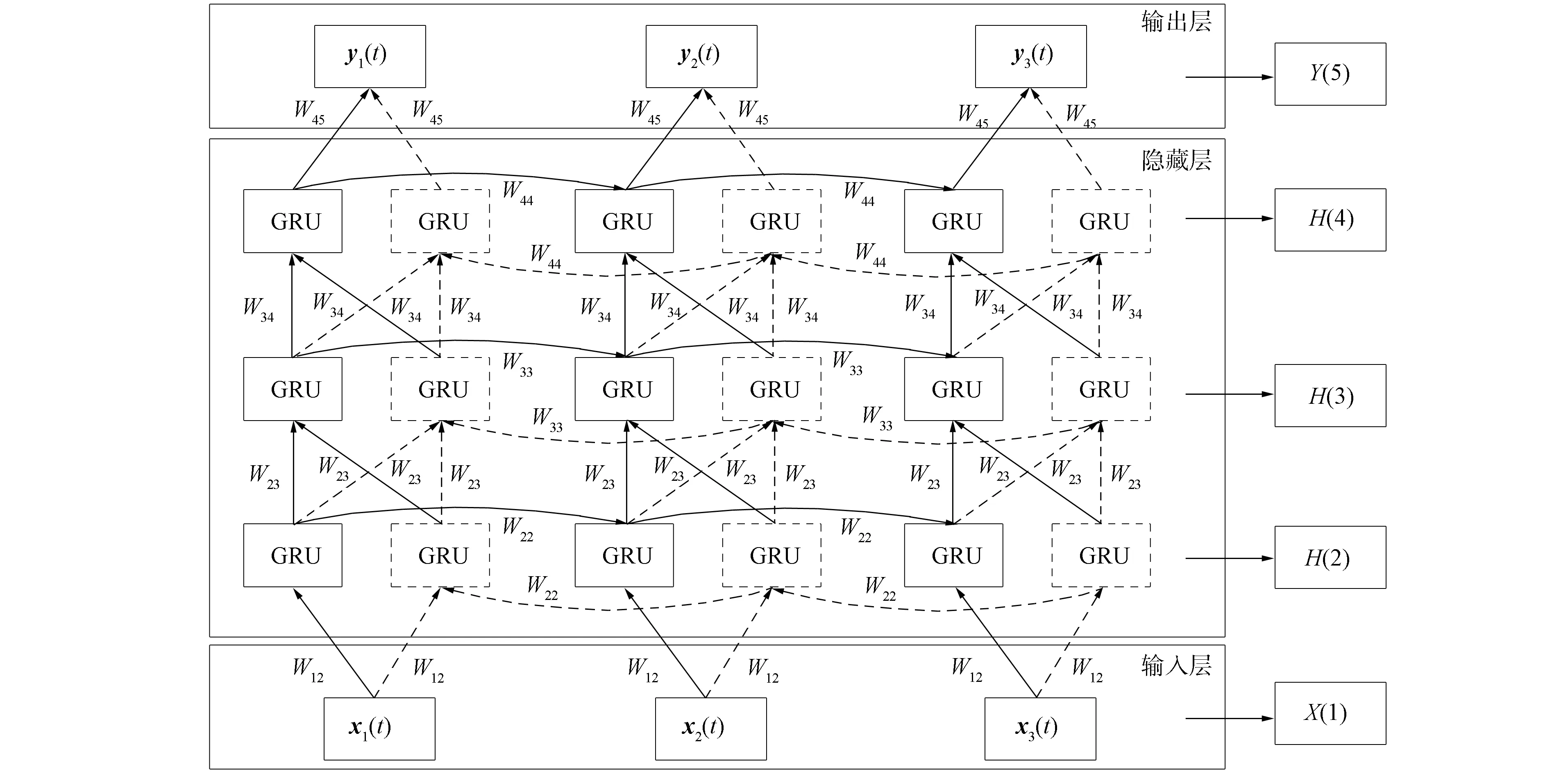
图3 深度双向GRU循环神经网络模型Fig.3 Deep bi-directional GRU-RNN model

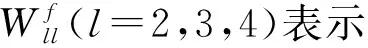
误差函数定义为

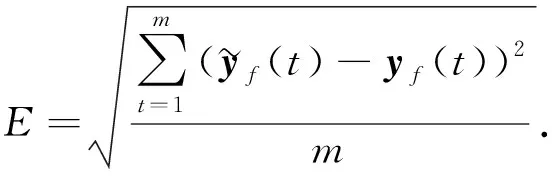
(9)

输出层权值梯度为

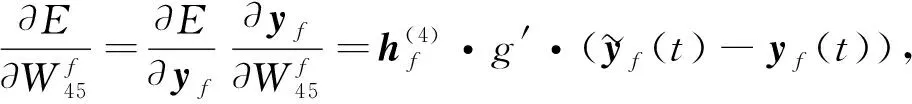
(10)

其中g′为激活函数的导数.令

则

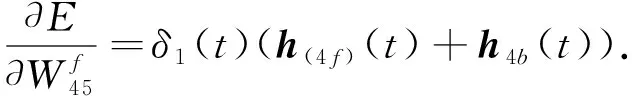
(11)

根据链式法则可推出

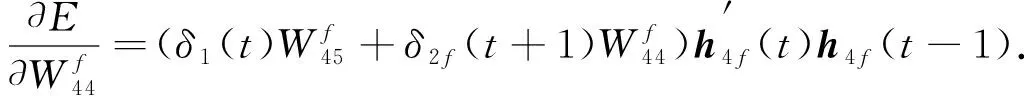
(12)

令

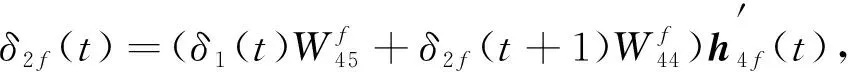
则第三GRU隐层参数梯度可计算为

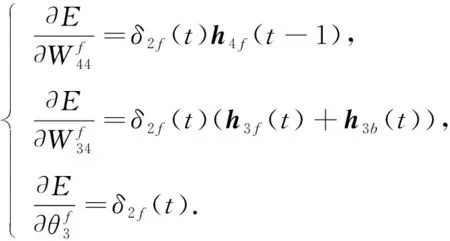
(13)

依次类推, 可得其余各层权值及阈值梯度计算公式为

(15)

在DBGRU-RNN网络模型中, 正向层中各参数调整的公式不相同, 本文按照统一的规则进行调整, 该规则用公式可表达为

β(t+1)=β(t)+αΔβ(t+1),

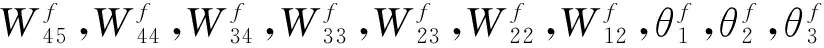
2.2 微地震降噪方法

构建基于DBGRU-RNN的微地震数据降噪方法, 旨在利用该网络模型训练到含噪微地震数据与纯净微地震数据间的映射关系. 设X,Y表示纯净微地震数据信号, 则有

Y=F(X+ξ),

(16)

其中F表示构建的网络模型,ξ表示高斯噪声.

模型的目标是构建加入噪声后的微地震数据与纯净微地震数据之间的映射关系, 则输入实际微地震数据至网络模型后对应的输出即为降噪后的信号S, 则S与Y之间的关系可表示为

S=Y.

(17)

2.3 数据预处理及评价指标设置

由于实际中无法获取到完全纯净的微地震信号以及含噪微地震信号中的噪声信号, 因此为构建DBGRU-RNN模型训练时所需的微地震数据集和噪声数据集, 本文采用Ricker子波正演的方式, 合成微地震信号作为仿真实验中的纯净数据. 采用高斯噪声作为噪声信号, 在纯净微地震信号中加入高斯噪声作为含噪微地震信号, 含噪微地震信号及纯净数据分别作为输入输出样本数据集. 其中样本数据集分为两部分: 一部分为训练集, 另一部分为验证集.

在评价基于DBGRU-RNN的微地震降噪方法的性能时, 本文采用4个评估指标进行评估分析, 分别为用于衡量信号是否失真的峰值信噪比PSNR(peak signal-to-noise ratio)[19], 反映一个数据集离散程度的均方差MSE(mean square error), 反映变量之间线性相关程度的相关系数CORC(correlation coefficient)[12]以及反映变量之间相近程度的能量比ER(energy ratio)[20]. 设纯净微地震信号为X, 降噪后微地震信号为Y, 则4个指标的计算公式分别为

其中X与Y越接近, 峰值信噪比越大, 均方差越小, 相关系数及能量比越接近于1.

2.4 仿真测试

本文使用MATLAB2014进行仿真实验, 通过在由Ricker子波正演得到的微地震数据信号中加入高斯噪声模拟含噪信号. 本文共生成48 000道数据, 每道数据采样点为400, 其中40 000道为训练集, 8 000道为测试集. 为便于观察降噪效果, 设置生成微地震数据图的道数为80. 图4(A)为纯净微地震数据, 图4(B)为加入高斯噪声后的微地震数据.

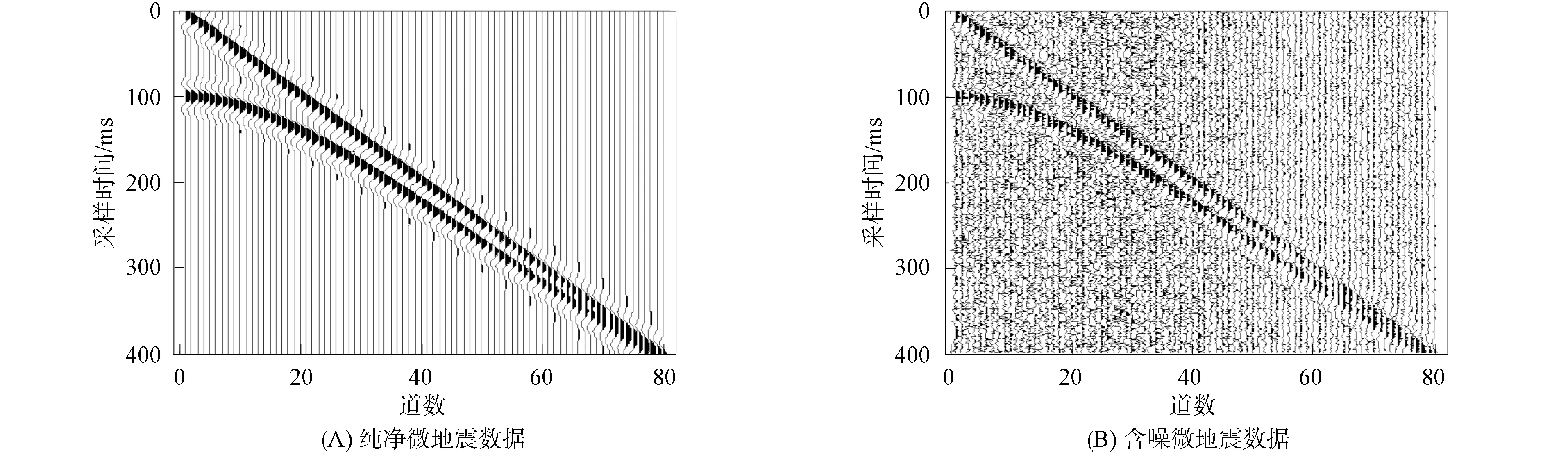
图4 纯净及含噪微地震数据集Fig.4 Pure and noisy microseismic data sets

本文输入数据为三维数据, 具体格式为(批量大小,序列长度,输入层节点), 其中序列长度为每道微地震数据的采样点数, 即400. 输入层节点数为每个样本中的微地震道数, 本文取80. 经过实验, 批量大小设置为20, 此时样本共有600/20=30批, 其中训练样本25批, 测试样本5批. 单条样本的数值列于表1.

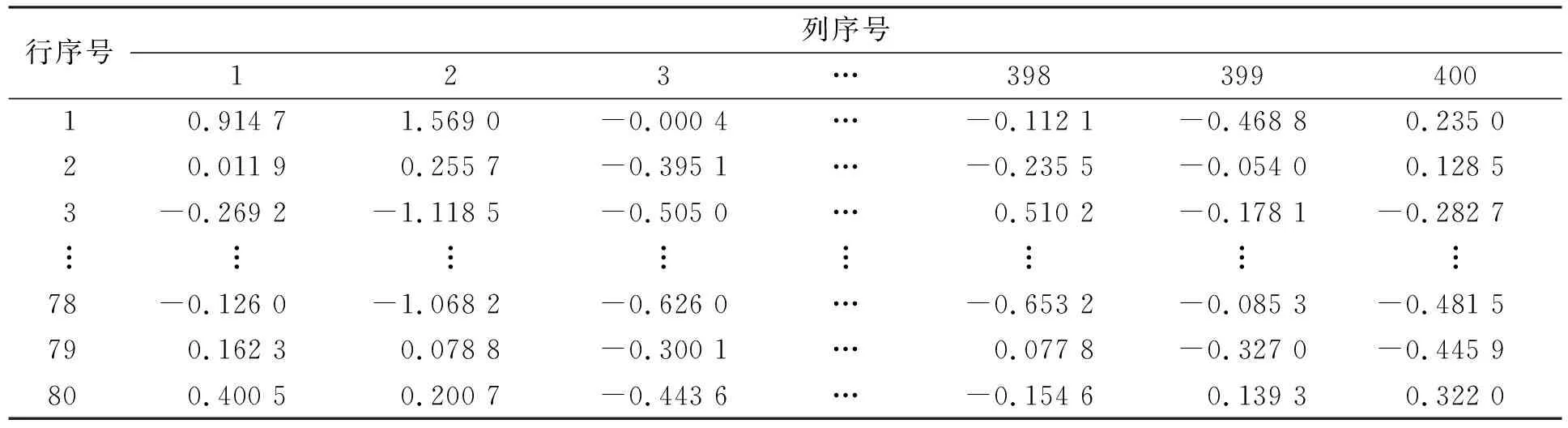
表1 输入数据示例

网络参数设置如下： 根据仿真数据并经多次实验, 网络的输入层节点设为80, 3个GRU隐藏层节点设为256,512,512, 输出层节点设为400, 所有激活函数均采用Sigmod函数. 网络训练采用期望输出与实际输出之间的均方误差作为损失函数, 使用Adam优化器在每次迭代过程执行参数调优. 学习率初值设为0.01, 且随迭代步数按α=0.8α递减, 学习率最小值限定为10-6. 迭代步数设置为50.

本文采用基于DBGRU-RNN的微地震数据降噪算法, 将其与普通循环神经网络、 基于LSTM循环神经网络的降噪算法[21]、 高斯降噪[22]、 BP神经网络降噪[23]等4种方法同时独立对含噪微地震信号进行降噪处理, 并对所得结果在降噪波形及评价指标两方面进行对比分析.

用本文降噪方法与其他4种降噪方法对同一含噪微地震信号进行降噪处理, 其降噪波形结果如图5所示, 其中： (A)为加入噪声后的微地震信号； (B)～(F)分别为利用不同方法降噪后的微地震信号.

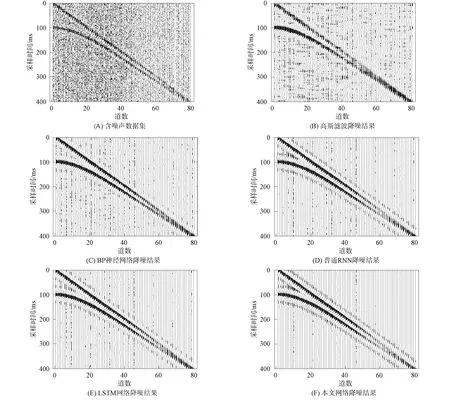
图5 不同降噪方法对微地震数据的降噪结果Fig.5 Denoising results of different denoising methods on microseismic data

由图5可见： 图5(B)为高斯方法降噪后的微地震信号, 与图4(A)的纯净微地震信号相比, 高斯方法降噪后的微地震信号存在大量噪声, 有效信号部分被噪声腐蚀以至于无法识别； 图5(C)为BP神经网络降噪后微地震信号, 与图4(A)的纯净微地震信号相比, BP神经网络降噪后的微地震信号存在明显噪声, 仅有非常少的微地震信号被恢复； 图5(D)和图5(E)为普通循环神经网络及LSTM循环神经网络降噪后的微地震信号, 可以明显观察到噪声, 与图4(A)的纯净微地震信号相比, 部分有效信号被恢复； 图5(F)为本文提出的DBGRU-RNN网络降噪后的微地震信号, 可见噪声基本去除, 仅残留少量噪声, 有效信号部分可清晰分辨, 与图4(A)的纯净微地震信号相比波形基本相近. 仿真测试结果表明, 本文提出的DBGRU-RNN降噪方法相比于其他4种降噪方法降噪效果较好.

为明确对比效果, 本文对加入噪声后的数据分别计算其PSNR,MSE,CORC和ER, 计算结果为: PSNR=1.828 3, MSE=0.656 4, CORC=0.088 6, ER=5.320 9. 5种降噪方法降噪后各评价指标的结果列于表2.

表2 5种降噪方法降噪后各评价指标的结果

由表2可见: 首先, 高斯降噪方法取得的峰值信噪比小于20 dB, 说明该方法的降噪结果失真过大, 得到的结果不可接受; BP神经网络及普通循环神经网络降噪方法取得的峰值信噪比大于20 dB, 小于30 dB, 说明得到的降噪效果较差; LSTM循环神经网络与本文网络降噪前后相比, 虽然信噪比均大于30 dB, 但结合图5(E)与图5(F)所示的微地震信号表明本文网络得到的降噪效果更好； 其次, 经本文降噪方法处理, 降噪前后信号之间的相关系数值为0.933 5, 说明本文方法处理后的数据与纯净数据基本一致, 而其他方法的相关系数值均低于0.8, 因此与其他4种方法相比, 本文方法的降噪效果最好； 最后, 本文方法降噪前后能量比最接近1, 其他4种方法的能量比均大于本文方法, 进一步说明本文方法降噪后的结果更接近于纯净微地震数据. 利用本文提出的DBGRU-RNN模型降噪后与降噪前微地震信号的峰值信噪比相比约提高36 dB, 且信号之间的相关系数值由0.088 6上升至0.933 5, 能量比最接近于1. 因此, 本文的降噪方法优于其他4种降噪方法.

3 实际应用效果及分析

3.1 矿场资料数据

本文选取大庆油田某井进行水力压裂时监测的微地震信号作为实测数据, 图6是截取其中700个采样点和全部地震道的结果. 由图6可见, 微地震数据中存在大量的噪声干扰, 其中第5道和第27道噪声干扰较大, 无法直接确定微地震信号的位置. 因此, 为更清晰地观察到微地震信号, 本文随机选取几条可明显观察到有效微地震信号的地震道进行波形显示, 如图7所示.

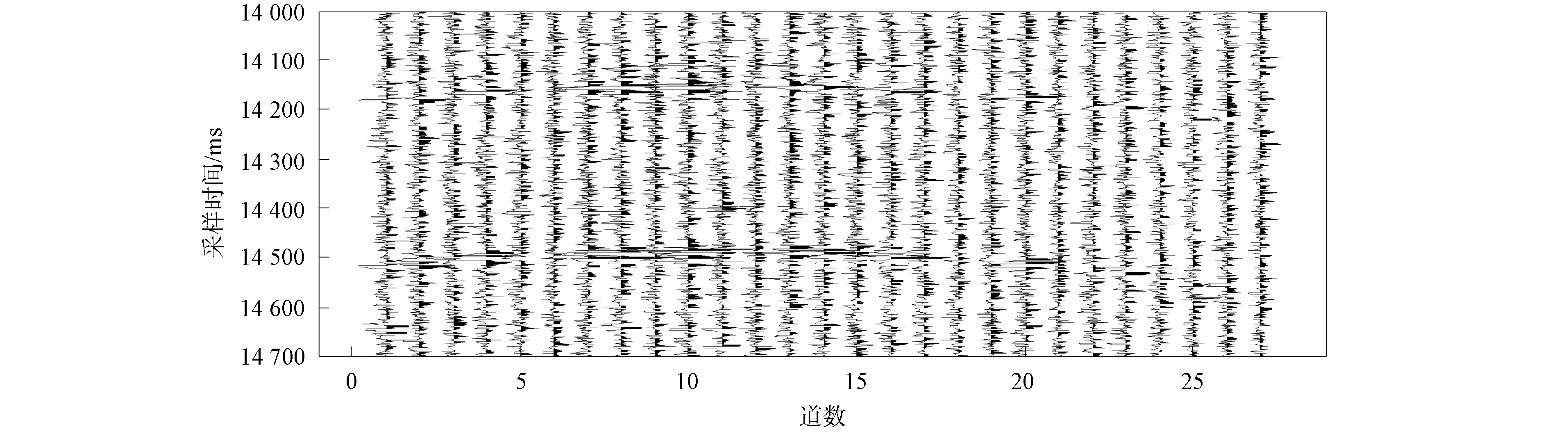
图6 截取部分微地震信号结果Fig.6 Interception of partial microseismic signal results

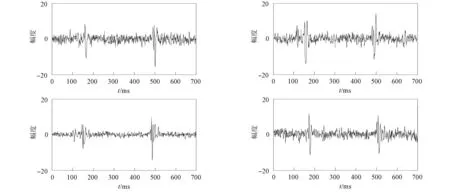
图7 单道微地震信号Fig.7 Single microseismic signals

3.2 降噪效果及分析

实际微地震数据中存在着大量的噪声干扰, 其噪声相比于本文添加的高斯噪声更复杂, 湮没了有效的微地震信号. 本文使用DBGRU-RNN网络模型对实际的微地震数据进行处理, 在对实测数据进行降噪处理过程中, 网络模型参数仍采用仿真测试中的网络模型参数进行设置. 为清晰观察DBGRU-RNN模型的效果, 使用单道微地震数据进行波形分析, 如图8所示. 由图8可见， 经本文模型处理后, 消除了部分噪声信号, 有效微地震信号显现更清晰.

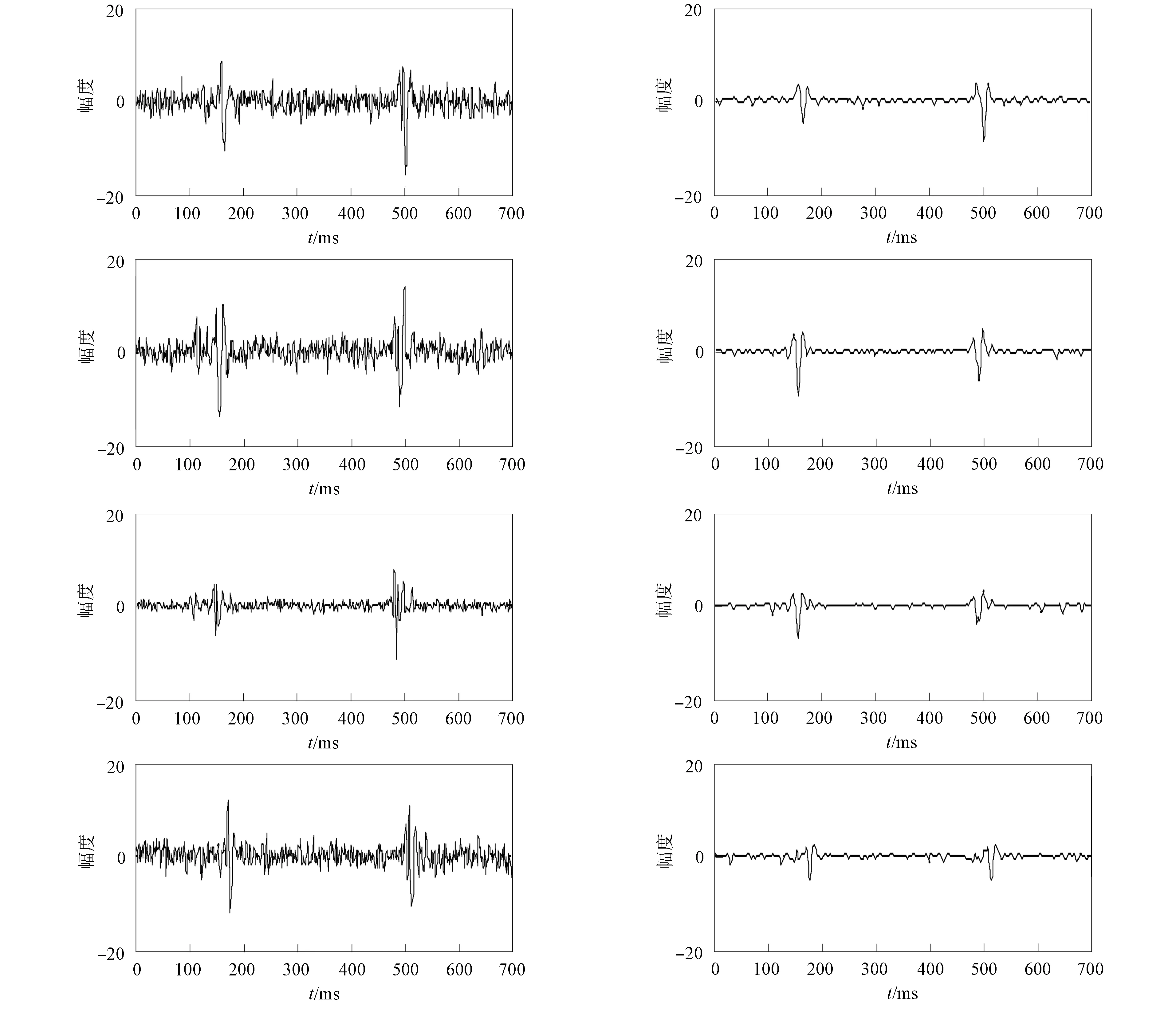
图8 实测数据降噪结果Fig.8 Denoising results of measured data

为进一步验证本文网络模型的有效性, 采用Walsh平均功率法对降噪前后的数据进行功率谱估计, 结果如图9所示. 为清晰观察本文网络模型的降噪效果, 实验将仿真数据降噪后的功率谱与实测数据降噪后的功率谱进行对比. 图9中, (A)为仿真含噪微地震数据降噪前功率谱, (B)为仿真含噪微地震数据降噪后功率谱, (C),(E),(G),(I)和(D),(F),(H),(J)分别对应图7所示4道单道微地震信号降噪前与降噪后功率谱. 由图9(C),(E),(G),(I)可见, 有效微地震信号均被复杂的噪声所腐蚀, 无法观察到有效信号的特征及曲线分布. 由图9(D),(F),(H),(J)可见, 经本文网络模型处理后, 有效去除了部分噪声, 可分辨出有效微地震信号, 并且将图9(D),(F),(H),(J)所示的功率谱曲线与图9(B)所示的仿真微地震数据降噪后功率谱曲线进行了对比, 结果表明, 二者的功率谱曲线在总体趋势上保持一致, 进一步说明本文方法能有效消除微地震数据中的部分噪声.

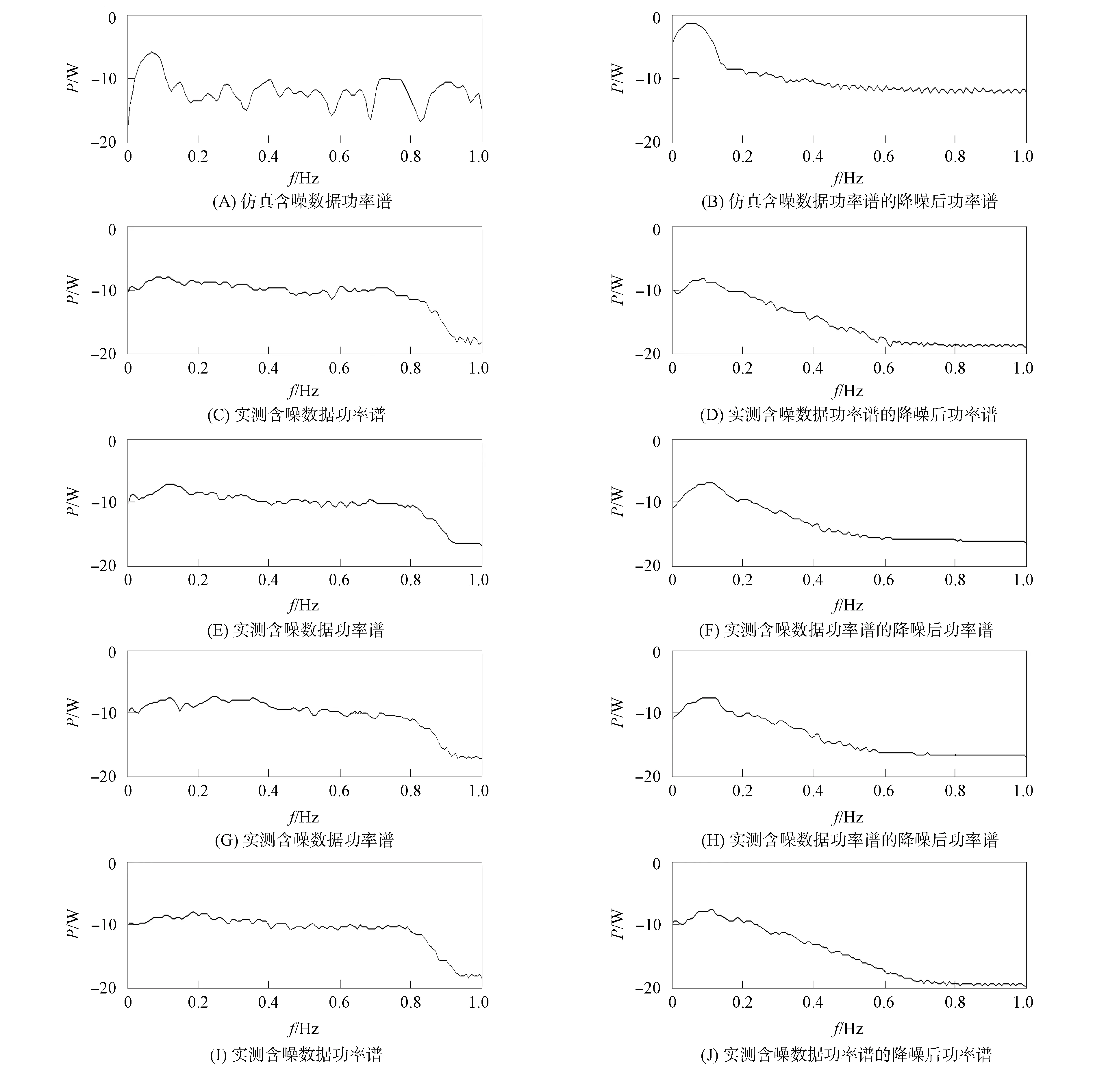
图9 实测数据降噪前后功率谱对比Fig.9 Power spectrum comparison of measured data before and after denoising

由图8和图9可见, 本文方法虽然能有效消除微地震数据中的部分噪声, 但仍有部分噪声存在影响微地震信号的识别, 与仿真实验中得到的结果相比降噪效果较差. 这可能是因为实测数据中噪声信号极复杂, 而在仿真实验加入的高斯噪声无法完全模拟实际噪声数据所致. 但在计算效率上, DBGRU-RNN比普通循环神经网络低. 这是因为DBGRU-RNN采用了比普通循环神经网络更复杂的隐层循环单元以及网络结构, 这些复杂操作使得DBGRU-RNN模型的性能得以提升.

综上所述, 本文针对微地震信号中存在大量噪声干扰, 导致其识别困难的问题, 提出了一种深度双向门控循环单元循环神经网络的方法, 并将其应用于微地震数据降噪中. 首先利用Ricker子波正演生成模拟微地震数据集, 采用高斯噪声作为噪声数据集, 然后利用构建的数据集验证本文构建的网络模型的有效性及准确性, 最后选取4种降噪方法与本文方法进行对比. 仿真实验结果表明, 本文方法与其他4种方法相比, 降噪效果更好. 进一步, 本文选取大庆油田某井进行水力压裂时监测的微地震信号作为实测数据, 再次验证了本文网络模型的有效性. 由于实测数据中的噪声极复杂, 而本文仿真实验中添加的高斯噪声无法完全模拟实际噪声, 因此在实际应用中, 虽然本文提出的模型能在噪声较大的情况下获得良好的降噪效果, 但仍存在少量噪声.