通过建立一维模型讲解两相流数值模拟过程

周 豹，杨 娜，胡永茂，谢再新，段卓琦，罗 亮，Gretar Tryggvason

（1.大理大学，云南大理 671003；2.约翰霍普金斯大学，马里兰州巴尔的摩 21218-2681）

数值模拟/仿真被广泛应用在力学、能源、环境科学等教学中。一方面是因为数值模拟本身具有灵活、易于控制、可重复性好，能够预测参数变化、发现新的现象等特点，并随着计算机硬件性能发展能够解决的问题日益丰富，已成为科学研究的重要方法。完成一项数值模拟类似于完成一项实验，相对于实验，数值模拟在一些方面具有不受实验仪器、设备制约的优势，省时省力。例如飞行器的风洞实验结果与相应的数值模拟结果非常接近，而风洞实验花费的时间、经济成本要远远高于数值模拟。另一方面数值模拟能直观地给出参数的实时数据、变化特征，例如流体数值模拟中的速度、压力、阻力、温度、组分浓度、紊流特性、管道应力疲劳等。学生可以通过数值模拟体会参数变化之间的关系、参数变化给系统带来的影响，深入理解公式的推导过程，建立实际现象与抽象公式的直观联系，对学生形成逻辑记忆有很大的帮助。

两相流动是流体力学的一个分支，是单相流动的拓展，同时也是复杂多相流动（流体中同时存在固体、液体和气体、微生物等中的两种或几种）的基础。两相流动广泛存在于自然界和能源、医学、化工等领域。例如，整个地球的水汽循环、核反应堆中的沸水堆、血液循环系统都属于典型的两相流动问题。两相流是能源动力专业的主干课程，也是一些相关专业的必选课程。

流体力学中牛顿流体的问题描述基本都是NS（Navier-Stokes）方程的求解〔1〕。NS 方程的存在性与光滑性问题是千禧年七大数学难题之一，至今没有被解决，但不影响它在应用领域的重要地位和作用。可以通过离散NS 方程求数值解。离散求解的同时可视化即为流体数值模拟的过程。工程和科学研究一般采用三维数值模拟，三维数值模拟能够很好地展示流体的参数变化规律，但是计算量大，计算机时长。教学中为演示原理、讲解离散和计算过程，通常把三维问题简化为二维问题。即便如此，二维程序仍比较复杂，所需讲解的细节问题仍有很多，占用课时量大，很难在同一时间段完成，造成课程的不连贯。本文以气液两相流中典型泡状流为例，讲解在向上的管流、层流稳定状态下，气泡会分布于贴壁面处〔2〕现象的数值模拟过程。为了尽可能用较短的课时阐述整个数值模拟过程，使学生对问题的全貌和计算过程有全面认识，对二维问题进一步简化，只考虑截面一个方向的分布，结果能够很好地反应气体分布规律。所编写的Matlab 程序短炼，易于学习和讲述，为讲述二维、三维数值模拟的复杂过程提供过渡，同时也为学生提供简化问题、分析问题的思路。

1 两相均相流模型的描述

实际问题较为复杂，为了讲解原理首先应简化复杂问题，不考虑流动过程中可能伴随的液滴/气泡破裂、相变、热交换等问题，在原有对单相流动的理解基础上，进一步简化研究两相流模型。

利用两相流基本NS 方程建立一维数学模型。假设气相以小气泡的形式弥散在液相中，设截面方向x 处气相占比εg，平均气相占比，截面方向x 处液相占比为εl，平均液相占比和εg是位置x 和时间t 的函数。其中，下标l 代表液相，下标g 代表气相。气相和液相占比的关系为

x 处的密度为

平均密度

连续性方程为

动量方程〔3〕为

其中

2 连续性方程和动量方程的离散和计算过程

首先对各个参数进行初始化，其中设截面宽度H=2；截面含气率液相密度ρl=2.5；动力黏度系数μl=0.002 5；运动黏度系数；时间步长〔4〕方向步长单位坐标对应点的含气率初始化为

如图1 所示，在不考虑气泡的大小，气相均匀分布的情况下，为求得流体速度分布，对流体微元进行受力分析。为使流体微元两侧的黏性阻力相等便于分析，选择以中心点对称的微元，以为例，微元“面积”（对于一维线段，则为长度）为微元受力平衡：

图1 单相流体层流二维受力示意图

化简后两边同除2δl 可得到

剪切力又等于

两式联立得

积分得

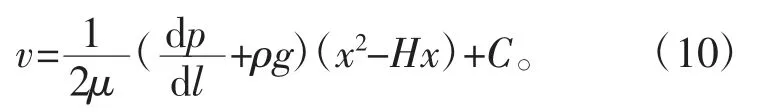
由边界条件w＝0，即v（H）＝0 得到C＝0，得到速度v 沿x 的分布

为计算方便，设气相密度为0，动量方程（4）可以改写成

采用一阶迎风格式计算Fg和mf，其中上标j 为时间点，下标i 为坐标点

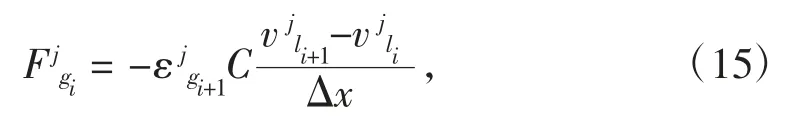
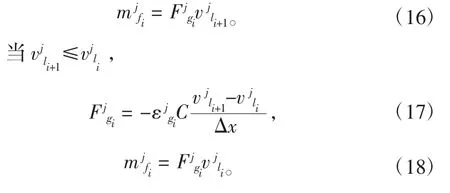
解出

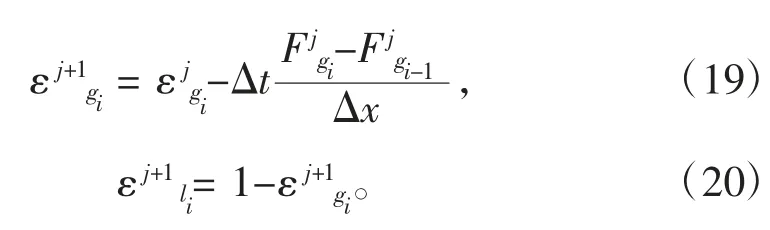
通过计算

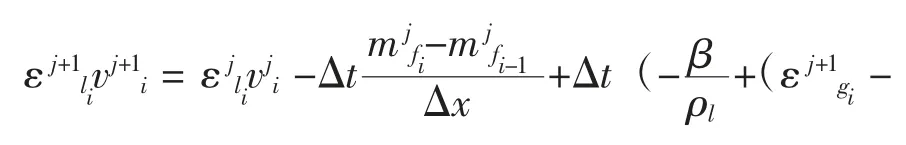
得到

图2a 为初始状态，其中速度分布为抛物形态，气相为均匀分布在横截面上。经过迭代计算，8 s左右之后，流体处于稳定状态，如图2b 所示，此时流体在管道中部速度分布基本保持均匀分布，气泡则集中在管道四周（一维则为两侧）。符合实验现象〔5〕。

图2 含气率和速度分布

3 结语

本文依据NS 方程对两相泡状流在二维管道截面方向上建立一维模型，通过离散NS 方程，设置初始条件，迭代计算流道内的液相速度分布、气泡分布，讲解两相流数值模拟的分析、计算过程。模型简单，所需编写代码简练，能够在较短课时完成讲解，易于学生掌握、理解原理及数值模拟整体过程，为后续学习打下良好的基础。