具有时变约束的机械臂系统自适应控制器设计
范永青,郝美荣
(西安邮电大学 自动化学院,陕西 西安 710121)
机械臂是模拟人体上臂的一种自动化机械装置,可以根据指令代替人工在危险复杂的环境下工作,实现工业机械化和自动化, 在工业制造[1]、航空航天[2]、医学[3]等领域均得到广泛的应用。通常的机械臂是一个多输入多输出的复杂非线性系统[4],并且具有高度耦合性、时变性的特点,因而对机械臂的轨迹跟踪控制一直是一个难点。面对复杂的使用环境要求,机械臂的控制系统必须具备良好的稳定性、实时性和较高的控制精度。
自适应控制通过设计出自适应律对被控系统的未知参数进行在线估计,然后利用参数估计值实时调整控制信号,从而有效地解决机械臂系统中存在的参数不确定性问题,使控制系统满足期望的跟踪性能。自适应控制具有强大的自学习能力,且跟踪效果取决于对系统中的未知参数估计的精确度,精确度越高,则跟踪效果越好。但在这个过程中需要大量的计算,与神经网络控制器[5]及模糊逻辑控制器[6]等结合使用,能够显著提高自适应控制对未知参数的逼近能力。
神经网络具有很强的容错性、鲁棒性和自学习能力。目前,常见的应用是利用其强大的逼近能力去补偿非线性系统中的不确定性。将神经网络与自适应控制相结合,增强了自适应控制在参数辨识方面的能力。由于自适应神经网络控制在参数辨识方面的独特优势,在很早之前便被引入到机械臂控制中[7-9]。Huang[10]设计了基于逆推设计方法的全局稳定神经网络控制,满足了一定的跟踪性能,但该方法只能应用于严格反馈系统。针对具有特定瞬态性能的双机械臂系统,Yang等[11]设计了一种新的全局一致最终有界(Global Uniformly Ultimately Bounded,GUUB)切换神经网络控制方法,但其中的径向基函数神经网络(Radial Basis Function Neural Network,RBFNN)的逼近精度不能自动在线调整。针对一类具有高度非线性结构的机械臂系统,在文献[12]中,提出了一种神经网络控制算法,获得了良好的控制性能。然而,这些研究在神经网络控制器的设计过程中没有考虑约束控制问题。
近年来,对于输出约束的研究多是引入合适的障碍李雅普诺夫函数[13-15](Barrier Lyapunov Function,BLF)防止系统状态违反响应的约束,其主要是通过约束系统误差实现间接约束系统输出。采用BLF进行约束控制设计的核心思想是要保证BLF在闭环系统中始终有界,当函数变量趋近于规定的边界时,BLF的函数值会趋向于无穷大。因此,只要保证函数的有界性就可以保证函数变量在设定的约束范围内,即可以满足系统的输出约束。在实际情况中,考虑到系统运行时的安全性和性能等因素,系统的输出约束控制占据了非常重要的地位。输出约束[16]的有界性是影响非线性系统稳定性的一个重要因素,为了使系统保持正常工作,必须使控制系统在保证内部信号有界的基础上满足设定的输出约束限制。根据约束边界,约束控制问题可分为常数约束和时变约束,相对于常数约束,时变约束更具实用性,更适合对实际控制系统的应用。为了满足系统的跟踪性能,在自适应神经网络控制设计中考虑了时变约束。文献[17]针对一类纯反馈非线性系统的输出时变约束跟踪问题,采用两个神经网络设计控制器,并利用BLF判断闭环系统的稳定性,但该方法只能保证半全局一致最终有界(Semi-Globally Uniformly Ultimately Bounded,SGUUB)。SGUUB的逼近只在一个已知的紧域上成立,必须预先保证这个域的精确范围,但在复杂系统中这种情况几乎不可能实现。因此,利用自适应神经网络控制方法进行全局稳定性控制设计更具一般性。
针对具有时变约束的机械臂系统控制器设计问题,拟设计一种基于BLF的自适应RBFNN切换控制器。根据RBFNN的逼近精度构造自适应律,利用BLF分析闭环系统的稳定性,并设计一个滑模面使未知机械臂系统的状态在超出预先设计的定义域时,能够通过自适应律在有限时间内到达滑模面。然后采用自适应RBFNN控制器使机械臂的输出满足时变约束,并使闭环系统中的所有信号满足GUUB。同时,通过设计参数自适应律与近似精度之间的关系,以期使RBFNN系统具有较高的逼近精度。
1 系统描述和预备知识
1.1 机械臂的描述和假设
机械臂作为机器人操作结构的重要组成部分,具有很强的灵活性,能够根据指令完成指定的动作,并能在各种场合发挥重要作用。二自由度机械臂系统示意图如图1所示。
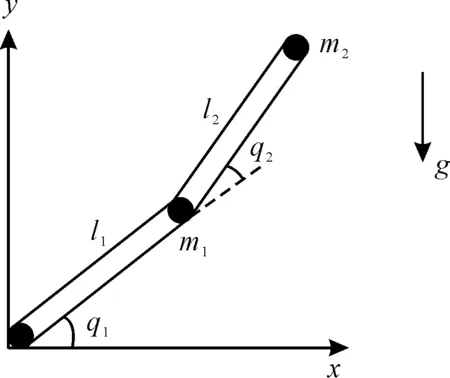
图1 二自由度机械臂系统
n连杆机械臂的关节角位置用n维向量q描述,其动力学方程[18]为
(1)
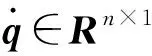
假设1[19]惯性矩阵M(q)是正定的且逆矩阵M-1(q)存在且已知。
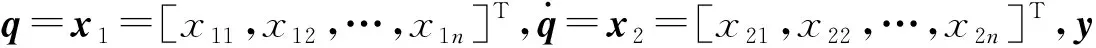
(2)
假设2非线性函数JT(x1)f+C(x1,x2)x2+G(x1)是未知的。
假设式(1)中的关节位置满足以下约束
(3)

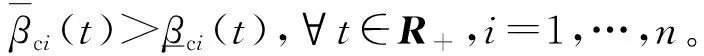


假设5对于在紧集U∈Rn给出的未知向量Ωi(X)=[Ω1(X),Ω2(X),…,Ωn(X)]T,函数Ωi(X)满足系数为li的利普席茨条件|Ωi(X1)-Ωi(X2)|≤li‖X1-X2‖。

定义βai(t)和βbi(t)分别为
(4)
(5)
跟踪误差被定义为
(6)
式中:η1=[η11,η12,…,η1n]T表示一个虚拟控制向量,能够使跟踪误差σ1收敛到一个以零为原点的邻域内。
误差参数的表达式为
φi=pi(σ1i)φbi+[1-pi(σ1i)]φai
(7)
且φai=σ1i/βai,φbi=σ1i/βbi,如果σ1i>0,pi(σ1i)=1,否则,pi(σ1i)=0。

引理2[21]如果-βai(t)<σ1i(t)<βbi(t),那么可以得到-1<φi(t)<1。
1.2 RBFNN系统的描述
RBFNN的网络结构简单,具有强大的自学习能力,且能够以任意精度逼近任何非线性函数,有效地处理系统中存在的不确定项,从而能够提高控制器的性能。
针对机械臂系统的未知非线性问题,在传统的RBFNN上配备了非零参数ρ和限制器,其结构如图2所示。

图2 具有非零参数ρ和限制器的RBFNN结构
由图2可以看出,RBFNN的输入中加入了模拟器1/ρ,然后X/ρ输入限制器。模拟器和限制器的作用是将输入向量X限制在RBFNN的逼近域上。
根据带参数ρ和限制器的RBFNN的原理,最终的输出可表示为
(8)
式中:X=[X1,X2,…,Xn]T;W=[W1,W2,…,Wn]T表示RBFNN的权值;Ψ(X/ρ)表示径向基函数向量。通常选用径向基函数作为高斯函数形式[22]
(9)
式中:‖*‖表示2范数;ck=[ck1,ck2,…,ckn]表示神经中心,(k=1,2,…,n);bk是高斯函数的宽度。
引理3[23]考虑到不确定连续非线性函数Ωi(X)满足系数为li的利普席茨条件,将RBFNN定义为Fi(X)且近似误差εi满足万能逼近supX∈U|Ωi(X)-Fi(X)|≤εi。在紧集U={X‖X‖≤α|ρ|},则可以得到
(10)
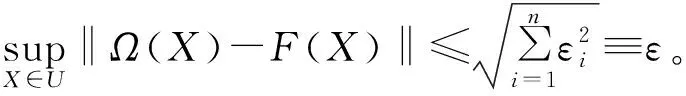

2 RBFNN控制器设计
为了保证系统的输出满足时变约束,选择李雅普诺夫函数
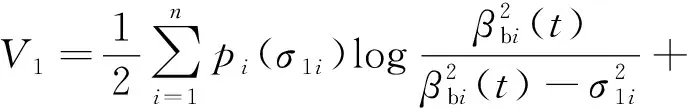
(11)
已知当|φ1|<1时,V1是连续可微的。因此,可以得到以下结果
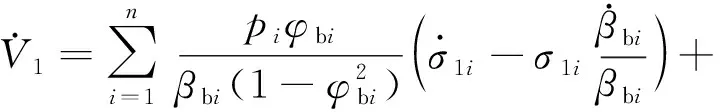
(12)

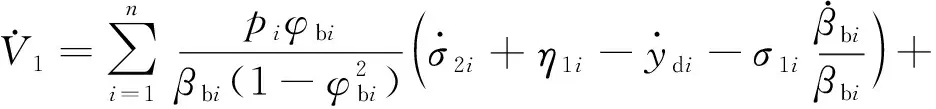
(13)

(14)

根据式(6),将式(13)改写为
(15)
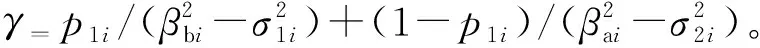
(16)
根据控制要求,提出RBFNNS自适应开关控制器,表达式为
(17)
其中,
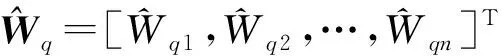
并设计了以下自适应律,且所设计的自适应律可以在线调整逼近精度

(18)
(19)
(20)
(21)

情况1‖σ2‖>α|ρ|
(22)
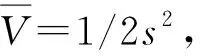
(23)


(24)
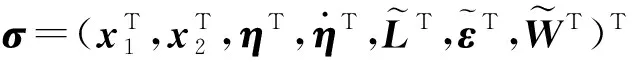
情况2‖σ2‖≤α|ρ|
考虑到‖σ2‖≤α|ρ|,因此选择李雅普诺夫函数
(25)
V2的导数为
(26)


(27)
根据式(17),可知
(28)
将式(28)代入式(27),可以得到
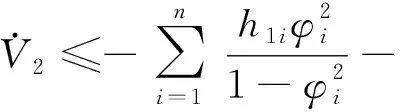
(29)
用式(29)可以定义候选李雅普诺夫函数为
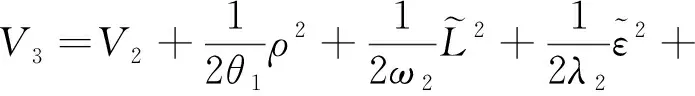
(30)
对V3求导,可得
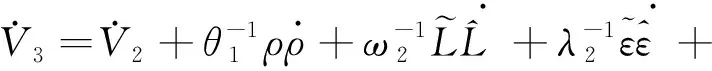
(31)
考虑到不等式
(32)
(33)
(34)
且将式(32)、式(33)和式(34)代入式(31),得到

(35)

(36)

(37)
根据式(7),可以得到以下有界条件
(38)
其中,
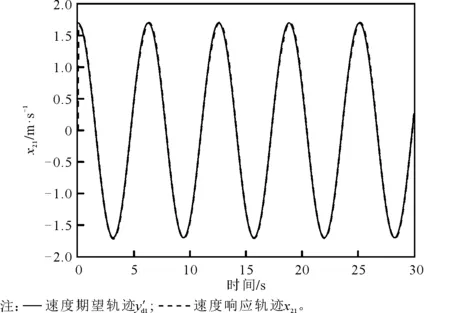
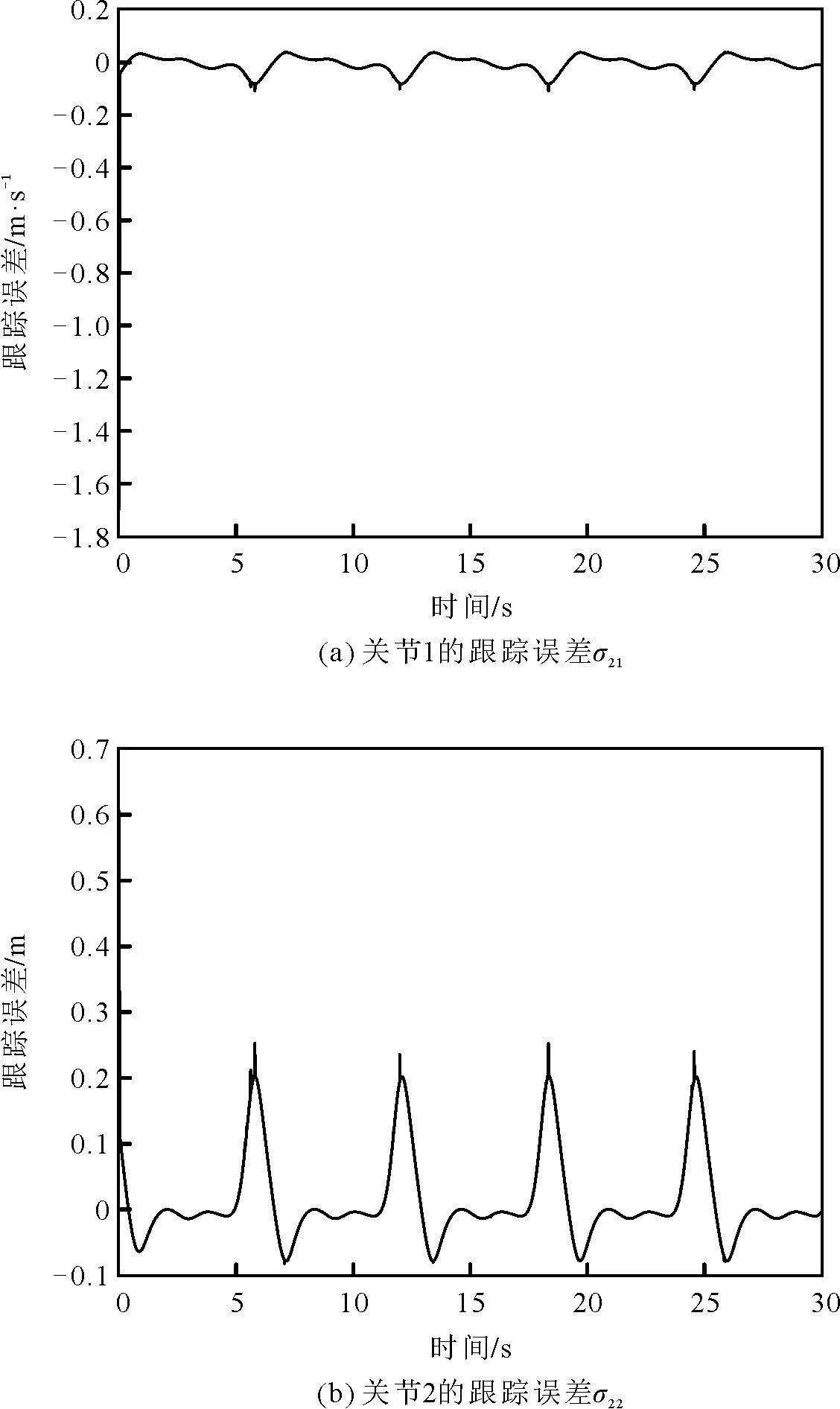
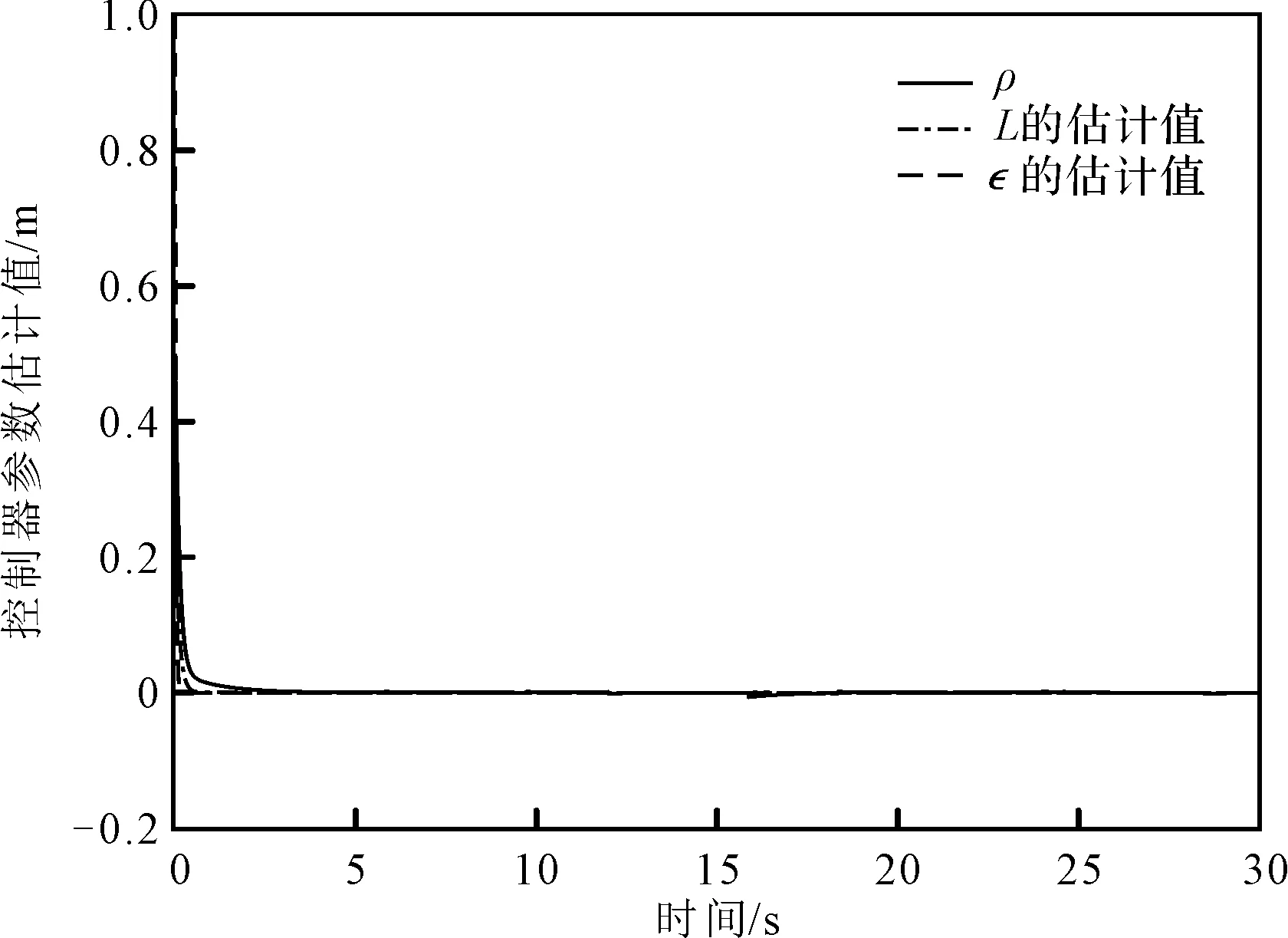
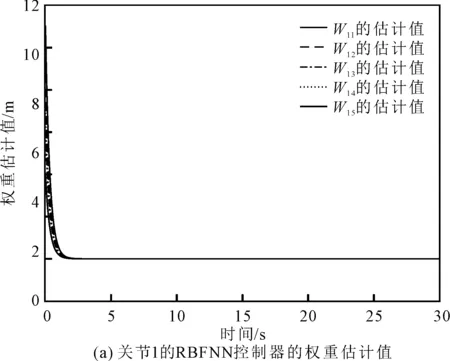
ydi(t)-βai(t) (39) 从证明过程可以看出,控制算法的全局稳定性过程描述如下。 1) 当‖σ2‖>α|ρ|时,通过自适应律式(18)至式(21)使跟踪误差到达滑模面s=0。利用该滑模面,未知机械臂系统的状态即使超出了预先设计的定义域,也会通过自适应律进入近似域。 2) 根据滑动模型表面s=0,‖σ2‖≤α|ρ|可以得到保证。因此,在U的近似域U={X|‖X‖≤α|ρ|} 上,利用上述RBFNNS逼近机械臂的未知模型。 由此得出,无论跟踪误差和闭环系统的状态是在RBFNNS的逼近域之外还是在逼近域内,通过所提出的控制方法都可以实现GUUB。 为了验证上述RBF神经网络自适应控制器,选择了一个二自由度的机械臂进行仿真验证,所用到的仿真工具为MATLABR 2016a。动态机械臂系统(1)的参数可选取以下数值 m1=2 kg,m2=1 kg,l1=0.35 m, lr1=1/2l1=0.175 m,l2=0.8 m,lr2=1/2l20.4 m, I1=0.052 50 kgm2,I2=0.131 25 kgm2,g=9.8 m·s-1。 其中, 选择理想轨迹信号为 yd=[yd1,yd2]= 约束力取值为 f(t)=[cos(t)+1.9,2 sin(t)+1.23]T 时变的下约束βc1和上约束βc2取值分别为 βc1=[βc11,βc12]=[sin(t)-0.4,0.9 cos(t)-3.5]T 使参数h11=0.1,h12=0.3,h21=2 000,h22=1 500。机械臂系统的跟踪性能仿真结果分别如图3至图10所示。 图3 关节1的输出x11对期望信号yd1的跟踪 在仿真结果中,图3和图4给出了在时变输出约束下关节1和关节2的输出和期望信号的跟踪轨迹,由图3和图4中可以看出,输出和期望信号均未违反约束条件,且实际轨迹都能成功地沿着期望轨迹运动。 图4 关节2的输出x12对期望信号yd2的跟踪 图5和图6分别表示关节1和关节2对速度期望信号的跟踪。由此可以看出,速度响应轨迹和速度期望轨迹的曲线几乎重合,通过所设计的控制器使机械臂的两个关节的运动速度都能够成功跟踪期望速度。 图5 关节1的速度响应曲线跟踪轨迹 图6 关节2的速度响应曲线跟踪轨迹 图7(a)和图7(b),图8(a)和图8(b)分别表示关节1和关节2的跟踪误差,从图7和图8可以看出,关节1的跟踪误差σ11能够控制在0.05 m以内;关节2的跟踪误差σ12能够控制在0.1 m以内;关节1的跟踪误差σ21可被控制在0.1 m以内;关节2的跟踪误差σ22可被控制在0.2 m左右。由此可得出结论,机械臂的两个关节的跟踪误差可以收敛到很小的以零为原点的邻域中。 图7 跟踪误差 图8 跟踪误差 所设计的神经网络控制器中的自适应参数可以自动在线更新。图9为控制器中的自适应参数响应关系,即式(17)至式(20)中自适应参数响应关系,图10(a)和图10(b)分别表示两个关节的径向基函数神经网络控制器的权重估计值的时间响应。由图9和图10可以看出,能够于2 s内在很小的以零为原点的邻域内趋于稳定。 图9 控制器中的自适应参数响应关系 图10 RBFNN控制器的权重估计值 以上仿真结果说明,所提出的控制方法是有效的,并且在给定的输出时变约束条件下可以获得良好的跟踪性能。 针对一类具有时变输出约束的不确定机械臂动态系统,提出了一种基于BLF的自适应RBFNN切换控制方法。选取合适的BLF分析闭环系统的稳定性,并设计了一个滑模面,使未知机械臂系统的状态在超出预先设计的定义域时,能够通过自适应律进入RBFNN的万能逼近域。再利用带有非零时变参数的自适应神经网络逼近机械臂动力学模型的不确定性,实现全局一致最终有界。与其他RBFNN控制器相比,该控制器的逼近精度可以自动在线更新。从仿真结果可以看出,该方法具有良好的控制性能。3 仿真结果及分析

[1.7 sin(t)+1,0.2 sin(t)+2 cos(t)-1.8]T
βc2=[βc21,βc22]=[1.9 sin(t)-1.5,1.5 cos(t)-1]T




4 结语

