“三度”视角：初中数学函数教学之探

姜国明

【摘要】函数及其图象内容的综合性、探究性等特点使教师觉得这类课内容难、内容多、学生“不肯动”，在规定的教学时间内探究活动难以顺利展开.如何行之有效地上好一堂函数教学课成为数学教师研究的方向.初中函数教学可以从“广度”“深度”“跨度”三个方面入手构建课堂，以“三度”视角引导学生来加深函数知识线索或专题的理解，让函数的教学变得清晰、厚实，从而打开函数学习之窗.

【关键词】函数;深度;广度;跨度

函数及其图象是初中数学的主要内容之一，也是初中和高中数学相联系的重要纽带.它与几何、代数、三角函数等知识有着密切的联系.中考命题中，既重点考查函数及其图象的有关基础知识，同时以函数为背景的综合题也是命题热点之一，多数省、市中考均用作压轴题.

一提到函数课，尤其是函数综合复习课，老师们都会面露难色.因为函数及其图象内容的“综合性”和“探究性”等特点使大家觉得这类课内容难、内容多，在规定的教学时间内探究活动难以顺利展开.内容因素和学生因素是函数课难上的客观原因，但这些因素真的是主要原因吗？笔者并不这么认为，笔者认为，最根本的原因还是因为我们没有找到有效的教学策略，所以才导致函数学习与探究课面临着重重困难.

用怎样行之有效的方法来上好一堂函数课或者函数综合复习课呢？笔者认为不妨依托串题模式，拾级而上，打造函数学习的“三度”高效课堂.在教学中选用同一个函数式为背景，将函数学习中需要重点掌握的知识点用该函数承载.通过对这个选用的函数不断增减条件，引导学生来加深函数知识线索或专题的理解，让函数的教学变得清晰、厚实.教学时通过对前期选定的函数进行计算积累，逐步清晰化该函数的数据背景，在此基础上构建的迁移变式问题就增加了探索的趣味性，无形中提升课堂教学的质量.笔者从“一网成擒拓广度”“一以贯之挖深度”“一波三折重跨度”三个方面进行函数学习的教学课堂探究，本文就从这三个维度来谈一谈教学实践与思考.

1“一网成擒”：拓宽函数基础学习的广度

万丈高楼平地起，再怎么强调基础的重要性都不为过.函数及其图象涉及的知识点很多：函数式待定、图象与系数的关系理解、图象的平移旋转变换、函数图象性质……借助串题，需将这些知识点尽可能地涵盖，在问题求解的过程中让学生深刻感悟，最终让他们在学习中建立起知识的前后相关联系，完善函数知识网络.

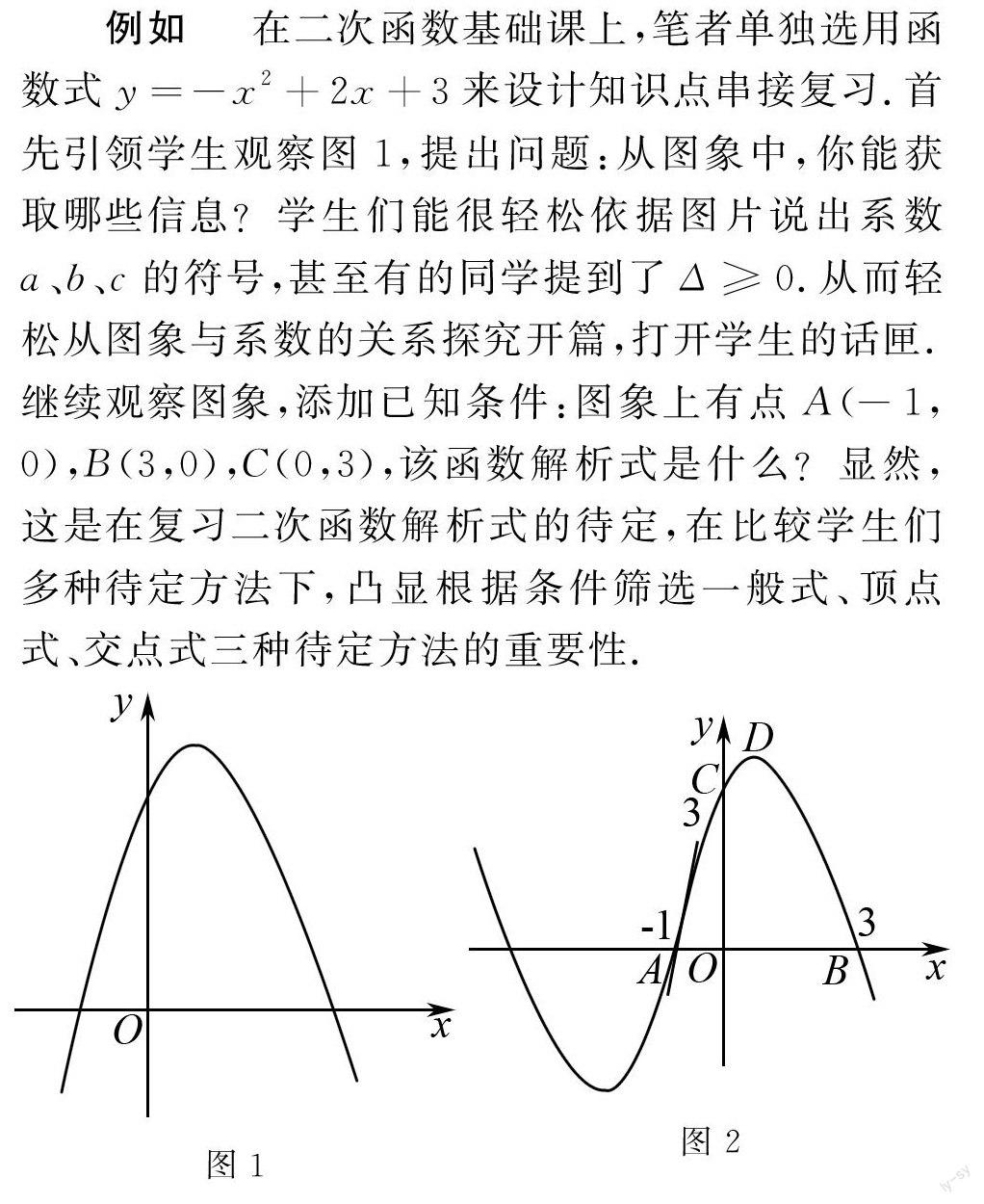
例如在二次函数基础课上，笔者单独选用函数式y=-x²+2x+3来设计知识点串接复习.首先引领学生观察图1，提出问题：从图象中，你能获取哪些信息？学生们能很轻松依据图片说出系数a、b、c的符号，甚至有的同学提到了Δ>0.从而轻松从图象与系数的关系探究开篇，打开学生的话匣. 继续观察图象，添加已知条件：图象上有点A（-1，0），B（3，0），C（0，3），该函数解析式是什么？显然，这是在复习二次函数解析式的待定，在比较学生们多种待定方法下，凸显根据条件筛选一般式、顶点

式、交点式三种待定方法的重要性.

紧接着，笔者要求学生计算出顶点D的坐标，并说出该函数的性质.学生根据计算所得，很快你一言我一语描述出了该函数的增减性、最值情况、y值的正负性情况.笔者则及时总结：函数的性质可以从观察图象开口和计算出图象的关键点来着手分析. 在同学们若有所悟间画风一转，继续提问：将二次函数y=-x²+2x+3繞A点旋转180°，旋转后的图象解析式是什么？如图2，笔者很清楚，这个地方学生一下子是解释不了的.在此处提出这个有点深度的问题，真正目的在于引导学生学会利用作图来印证函数式的待定，培养同学数形结合意识、探究意识、归纳意识.

解决了这个题后，后续的图象变换问题可以一一跟上，如问：y=-x²+2x+3沿x轴翻折后解析式是什么？沿y轴翻折呢？绕原点旋转180°呢？教学中当然可以继续添加线段、丰富图象画面.譬如过B、C作直线，问：令BC直线为y₁，抛物线为y₂，x为何值时y₂≤y₁？

显然，借助y=-x²+2x+3图象的基础学习课还可以衍生出更多内容.每个数学教师都是教学的设计师，相信动动脑筋就会有精彩呈现，我们的课堂会有更多不同的生成.基础维度的串题教学设计摆脱了重复冗繁的函数式计算、图象关键点（顶点、与x轴交点等）求解，去芜摘蔓，直奔知识考查主题.学生们能在有限的时间内接触更多的例题内容，拓宽知识复习的广度.课堂上再经历多次自主评析、提示再思考后，就能够逐渐总结出各种题设的解答思路与方法，内化成学生个人的学习经验.

2“一以贯之”：发掘函数专题学习的深度

专题学习课是教师开启学生心智、促进思维的重要课型之一.好的专题内容可以让学生从知识的初步认知向高一级的知识灵活应用转化，实现培养学生独立探索和创新精神的教学目标.但平常大部分老师的教学方式就是通篇就挑选的例题，一题一题往下讲，直到下课为止.少有重点，鲜有总结，就题论题.其实大家都知道能作为例题的教学内容通常有较强的典型性、延续性、示范性.教师如果忽略了对例题相关知识和方法的提炼发掘，只会是学生能“听懂”却无法举一反三，专题学习的效果就很难凸显出来.

数学教师应该做一个有心人，平常留意典型的教学例题，静下心来将一些能成系列的问题整理出来.将这些问题按难度层次排个序，串题设计由浅入深，循序渐进.难点问题突破时，在前面做好一小题的思路铺垫.当问题串接得丝丝入扣、接近学生的知识最近发展区时，相信学生的课堂表现会更加出彩！

例如笔者还是借助函数y=-x²+2x+3来设计一节面积问题的专题课，首先观察图3，连接AC、BC，请学生计算出△ABC的面积.由于目标图形规整，同学们能很快获取答案.

接着连接CD、BD，求四边形OCBD的面积.在与学生的讲解交流中不难看出，学生有着将图形划归成可求规整图形的基本意识.此时再在此基础上，继续抛出问题：连接CD、BD、BC，求△DBC的面积.例题难度提升后肯定有部分学生解题的思路受阻，但只要老师或者学生一提到四边形OCBD的面积的信息，绝大部分同学会恍然大悟，想到用四边形OCBD的面积减去△OBC的面积的方法.此时再设计让学生同步求解△ACD的面积或者介绍铅锤方向切法的基本计算方法，讲解的思路便顺势而上，学生们的探究必然兴致盎然.

专题继续加深，将静态面积问题串接上动态面积问题，知识传递保持螺旋上升.如图4，若P是抛物线右侧BC段上的一个动点，问何时△PBC面积最大？此时P的坐标是什么？抛物线上是否存在一个点M，使得△MBC和△BCD的面积相同？会不会有△MBC是△BCD的面积的2倍？

贪多嚼不烂，专题学习不应该是高难度例题的堆砌.借助串题将一个知识点穷极变化，一挖到底才是有效学习的王道.学生在知中去行，在行中去提升知.创意地捕捉，创造地生成.专题维度的串题，通过不断地概括化、言语化、简缩化而逐步向思维的抽象化转化，以达成学生认识和思维水平的深化，真正实现对知识的掌握.

值得注意的是，学生了解掌握专题知识点后也不能保证能顺利解决此类问题，只能说明学生通过问题的阅读与理解建构最初的叩门砖.肯定要随着外部综合题型的信息“接触”才能不断发生新的变化，成为学生真实的技能技巧，因此进行知识模型地再应用显得尤为重要.在作业设计中，笔者认为应该反其道而行之，有意识将串接知识模型的题目加以拆解，回归到不同的函数解析式中去，并根据难易程度拟出相应的多个练习内容，巩固和再挖掘学生课堂的理解的深度.

3“一波三折”：关注函数综合学习的跨度

函数综合题直指学生的数学素养，提升学生解决综合题的能力绝非一朝一夕就能做到.尤其是函数压轴题不是一两个专题学习就能够涵盖的.课堂上也许会遇到这样的情况：一道压轴题的讲解还没完，下课铃声就响了，老师们全力以赴地讲解和计算，留给学生动手探究的时间又能有多少呢？学生能理解多少知识呢？一个综合题各个小题所涉及的考查内容可能不尽相同，一会儿是动点问题，一会儿也许就成为相似问题.学生不适应大跨度的知识点考查是造成综合题难理解、难得分的重要原因之一.

有些综合学习课是需要打破章节的桎梏的.数学教师要注意收集和充分利用好函數压轴题资源，不断丰富自己的题库.致力于对典型的函数小题进行一定逻辑的组合拼盘或者改造加工.通过教师的串题加工可以呈现相关知识，并增加前后知识的跨度.学生往往能从内容的差异中找出不同的信息，并在教师的引导下通过比较来分析、综合，对知识点进行更深层次的解读，在练习中帮助学生提升思维能力.换句话说，只有让学生多接触一波三折的组合的题，多尝试克服综合题的层层阻挠，才能建立迎难而上的自信，消除畏难不前的心理阴影.

例如同样以函数y=-x²+2x+3为例，笔者考虑到特殊图形的探究是一类热门的题型，富含方程思想、分类思想，串题设计时以它起步.设计问题（1）：若点P是函数对称轴上的一点，当△ACP是等腰三角形，P的坐标是什么？稍作更改就可串接其他特殊图形问题;设计问题（2）：若点P是函数对称轴上的一点，当△ACP是直角三角形，P的坐标是什么？设计问题（3）：如图5，Q是抛物线上的一个动点，M是x轴上的一点，若以Q、M、A、C为顶点的四边形是平行四边形时，M的坐标是什么？

当学生们熟悉特殊图形求解的套路后，考虑继续转换阵地，添加图形全等、相似菜单;设计问题（4）：如图6，是否存在抛物线上的一个动点Q，使得△OCQ与△OBQ全等？又如问题（5）：是否存在抛物线上的一个动点E，作EF⊥x轴于F，使得△OCA与△OEF相似？

在平时的教学中应多给予学生一些教学对象背景的深刻思考和挖掘，提高学生的问题化归能力.跨度维度的串题教学则可以为学生探究思维多增添一些出发点.特别值得一提的是，跨度串题也要有一定的针对性，学生掌握薄弱的问题要多组合、刚出炉的新题型要多组合、富含数学思想方法的题要多组合. 值得注意的是，有些典型的好题是需要特定的数据背景，此时强行串题会增加学生计算结果的复杂性. 这个时候不妨单题单选，同样也能辅助开阔学生解题的视野.

4结语

总之，“三度”视角下的函数教学激发了学生有深度的课堂体验，实现数学思想价值的引领.拥有基础广度、专题深度、综合跨度的函数教学让我们的探究更接地气.当然，我们的课堂显然不仅仅是这三个维度，在践行函数全方位教学与学习的时候肯定有许多的交集，我们还可以从更多的维度去探寻出“四度”“五度”视角下的初中数学课堂.

参考文献：

[1]徐小建.例谈几何变式训练[J].中学数学杂志. 2015（09）：8-11.

[2]宋晓平.“新手—熟手—专家”型数学教师课堂教学的对比研究[J].数学教育学报，2013，（2）.