基于基体效应校正和对应分析的便携式X荧光光谱法对土壤重金属的研究

郭金珂，陆继龙，司峻石，赵 威，刘 洋，王天欣，来雅文

吉林大学地球探测科学与技术学院，吉林 长春 130026

引 言

近年来，全球人口的增长导致城市扩展到了农村地区[1]，重金属污染物通过人为活动释放进入土壤，包括工业生产、 废水灌溉、 车辆排放、 化肥滥用、 金属矿产资源开发、 电子垃圾等[2]。 由于重金属不易被微生物或化学物质降解，因此重金属在土壤中富集，并通过生物地球化学循环损害人类健康[3]。 为了了解大范围土壤重金属的环境风险，需要收集大量土壤样品，然后进行分析测试以获得足够的土壤重金属含量数据[4]。 因此利用快速筛选技术检测各种环境样品中的重金属已成为人们的迫切需要。

土壤中重金属可以通过这些常规分析技术测试，包括电感耦合等离子体质谱法(ICP-MS)、 电感耦合等离子体原子发射光谱法、 原子吸收分光光度法和原子荧光光谱法[5]。 这些方法虽然准确，但是所有样品都需要用溶液进行酸溶消解预处理，测试步骤较为复杂，耗时较长且成本较高，同时化学分析试剂对环境有害，容易产生二次污染[6]。 便携式X射线荧光光谱法(pXRF)是一种低成本、 快速简便的方法，与传统方法相比，该方法可以直接在现场进行快速、 无损测试[7]，并且可以同时分析多种元素，样品前处理简单，没有废弃物的产生[8]。 尽管pXRF不会取代ICP-MS等常规实验室分析方法进行高精度分析，但在允许较低的数据分辨率的情况下，pXRF在土壤污染调查中有良好的应用前景[9]。

pXRF发出的X射线强度可能受到土壤含水量、 矿物非均质性、 颗粒大小、 基质效应等的影响，其中主要来源于基体效应[10]。 样品的基质包括组成该样品成分的物理部分和化学部分[6]，物理基质是指颗粒大小、 均匀性、 异质性和表面条件的变化。 化学基质是指元素浓度的差异，地质样品中元素含量的差异受模式矿物学、 地质体成分、 热液和变质蚀变和脉状的控制。 基体效应指样品的基体通过引起吸收、 增强或光谱峰重叠等效应影响元素的分析[11]。

克服基体效应进行定量分析是pXRF研究中的热点和难点。 目前，pXRF定量分析方法包含两大类，一类是实验校正方法，包括内标法，标准加入法和稀释法等，一类是数学校正方法，包括基本参数法，经验系数法，神经网络校正法等。 实验校正方法主要通过对实验过程进行更精确地控制来减小基体效应所带来的误差，但是极大的增加了实验的工作量，且步骤较为繁琐，不易操作。 数学校正方法主要通过建立不同的数学模型和校正方程对得到的数据进行校正来达到目的，它没有改变实验的工作量，仅是需要增加一些数学计算，是目前较为常用的方法[12]。

大多数数学校正方法均是基于传统线性回归所进行的，受离群值影响较大，某些时候因为部分离群值的影响，使回归曲线出现较大的偏差。 或者在某些样品中，由于主量元素含量差距较大，导致对待测元素基体效应影响强度差距较大，采用传统线性回归法无法校正，严重扰乱测试数据的回归规律[6]。 因此本方法通过利用主量元素数据校正待测元素数据，进一步减弱测试过程中基体效应的影响。

对应分析，也被称为关联分析法，是近年来发展起来的一种新的多因变量统计分析方法。 它通过分析由定性变量组成的交互摘要表来揭示变量之间的关系。 可以揭示同一变量的各个类别之间的差异以及不同变量的各个类别之间的对应关系[13]。 传统的因子分析只能研究样本之间的关系(Q因子分析)或变量之间的关系(R因子分析)。 实际上，样本和变量之间通常存在关系。 对应分析可以同时分析样本和变量，已成为研究多元变量关系的重要方法[14]。

利用pXRF对吉林大学各校园土壤样品进行了Cr，Ni，Cu，Zn和Pb 5种重金属元素的快速测试，利用数学模型对测试数据进行了基体效应的校正，并与ICP-MS测试结果进行对比，探究了不同元素的主要影响基体元素。 分别计算了基体效应校正法与传统线性回归法所得到的数据的决定系数、 平均相对误差、 均方根偏差等统计学参数，对比两种方法的差异，探究基体效应校正法在不同元素间的适应性。 并用对应分析取代传统的因子分析，对不同元素及样品间的相关性进行了分析。

1 实验部分

1.1 研究区域

研究区域位于吉林省长春市(图1)。 坐标43°05′—45°15′N, 124°18′—127°02′E, 市区海拔在250～350 m之间，地势平坦开阔，属北温带大陆性季风气候区，年平均气温4.8 ℃，最高温度39.59 ℃, 最低温度-39.8 ℃，日照时间2 688 h[15]。

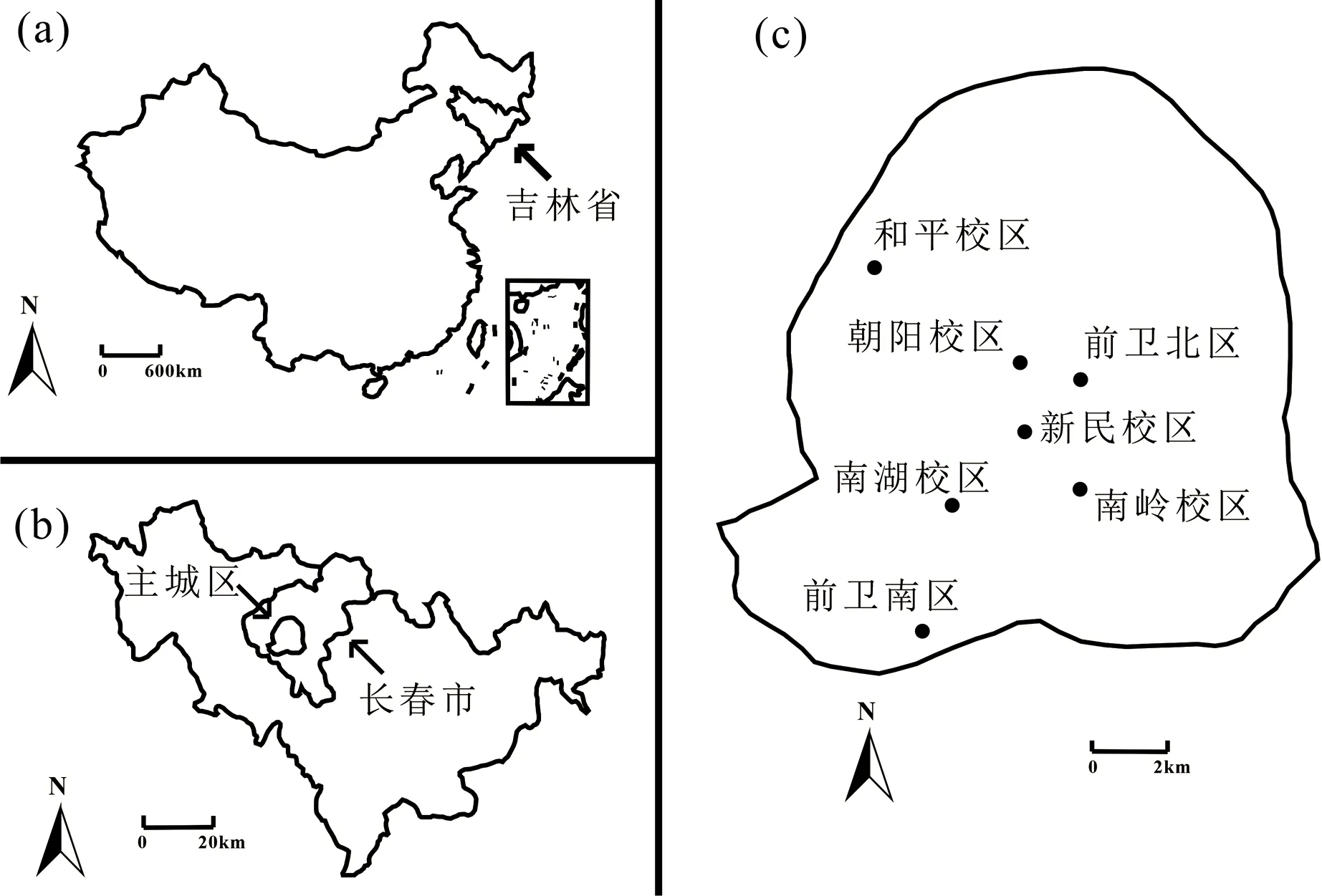
图1 研究区域及样品分布(a)： 中国； (b)： 吉林省； (c)： 长春市主城区Fig.1 Study area and sample distribution(a)： China; (b)： Jilin Province; (c)： Urban area of Changchun City

1.2 样品采集

样品采集自吉林大学前卫南区、 南湖校区、 南岭校区、 朝阳校区、 新民校区、 和平校区和前卫北区7个校区，每个校区根据面积大小采集2～12个样品。 样品采集点选在各校区花坛、 湖边、 树下等土壤出露处，尽可能分散以代表校区的大部分区域。 采集样品时，使用不锈钢铲在深度为0～20 cm的地方收集样品，草、 细枝和其他碎屑从样品中除去，在每个设计点周围选取3～5处分别采集土壤并均匀混合成为一个样品[16]。 每个样品点采集土壤1 000 g左右，并且分别编号，记录采样地点、 周围环境、 植被生长状况等信息。 同时取出部分样品用pXRF进行原位测试，测试方法详见下文。 然后将剩下的样品送至实验室。

1.3 方法

实验采用的分析仪器是能量色散型便携式X荧光光谱仪，来自英国牛津公司，仪器型号为X-MET7000，铑(Rh)阳极靶，电压40 kV，电流60 mA，最大功率2.4 kW，第四代硅漂移SDD探测器，元素周期表中12号元素镁Mg和92号元素铀U之间的元素均可分析，土壤测试模式为Soil_fp[7]。

每个样品采集时均取出部分在野外进行原位测试。 首先选取样品近地表较为干燥的一部分，并除去石子等杂物，置阳光下继续简单干燥十分钟左右，放入布袋中用木棒均匀的敲击，然后将样品填充进一个直径5 cm、 深2 cm的圆柱形容器内，将样品表面均匀压平，然后用pXRF扫描测试[17]。 测试时为尽量减小由于样品成分不均匀和操作失误而带来的测量误差，采取多处多次测量取平均值的方法，在每个土壤样品表面扫描五个点，每次扫描30秒，最后取5次测试的平均值作为该次测试的最终数据。 剩下取回实验室的部分送至吉林省地质科学研究所实验室进行ICP-MS测试。

1.4 数据处理

样品基质主要有K，Ca，Ti，Mn和Fe 5种常量元素组成，根据对元素间进行相关性分析，选择与待校正元素相关性最高的常量元素作为基体效应校正的主要元素[18]。 由原始谢尔曼方程[式(1)][12]可知，理论上所有元素之间均会互相影响，但是在实际计算时，由于测试准确度及计算量的问题，不可能将所有元素一一计算，因此对其进行简化，选取一种元素含量较高，受其他元素影响相对较少的常量元素作为主要影响元素，对其余待测元素进行基体效应校正，即式(2)。

Ii=f(Ci，Cj，Ck，…，Cn)

(1)

(2)

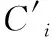
(3)

(4)

(5)

(6)

通过决定系数(R2)、 平均绝对误差(MAE)和均方根误差(RMSE)这些参数来估计pXRF测量值与ICP-MS测量值之间的准确度和精密度。R2用来评估pXRF测量值与ICP-MS测量值之间的线性相关性，R2值越大，两种测试值之间的相关性就越强[20]。 MAE用来评估仪器对于样品整体的测试值的准确度，MAE值越小，则实验结果越准确[21]。 RMSE用来评估仪器对于样品整体的离散程度，RMSE值越小，则测试值在真实值附近的波动幅度越小，实验结果越优[22]。

R2，MAE和RMSE的计算公式如式(7)—式(9)

(7)

(8)

(9)

利用对应分析对各元素及各方法间相关性进行分析，分析软件为IBM SPSS Statistics 21.0。

2 结果与讨论

2.1 基体效应校正

通过元素间相关性分析结果，确定出每个元素基体效应校正的常量元素(表1)，利用基体效应校正法和传统线性回归法分别对测试结果进行校正，通过观察两种校正方法的统计学参数(表2)和拟合图像(图2)，判断基体效应校正方程对数据的影响。

表1 各元素最大影响元素及各方法回归方程Table 1 Regression equation by methods and the maximuminfluencing element for each element

表2 各方法校正后的统计学参数及提升程度Table 2 Statistical parameters and degree of improvement after correction of each method

对比两种数据处理方法，通过传统线性回归法，除Cr和Ni的R2低于0.6外，Cu，Zn和Pb的R2均在0.8以上，而经过基体效应校正法处理后，所有元素的R2均有所提升，达到0.6以上，Pb更是达到了0.9以上，且MAE及RMSE相对于传统线性回归法均出现了不同程度的提升，即测试误差及偏差均被减小。 对比两种方法校正后的拟合图像可以看出，基体效应校正后的数据与y=x的接近程度更大，可以观察到，基体效应校正法主要通过校正离群值来实现数据质量的提高。 说明基体效应的校正方程有效，经过基体效应方程校正以后，可以得到更高质量的数据，相较于传统的线性

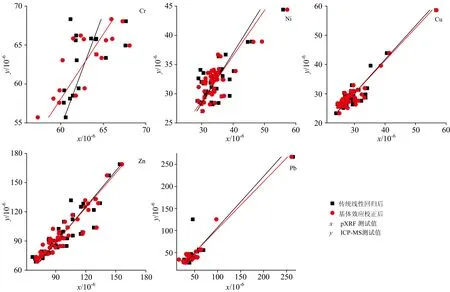
图2 校正后的pXRF数据与ICP-MS数据间的线性回归图像Fig.2 Linear regression images between pXRF data and ICP-MS data after correction

回归方法更加优化，在测试过程中，常量元素对重金属元素的测试有着一定的影响，这种影响仅通过传统的线性回归无法消除，而通过基体效应方程的校正后可以减弱此部分影响。

2.2 元素适用性

对比R2的提升程度，Cr的提升最大，近乎翻倍，其次是Ni和Pb均提升了10%以上，仅有Cu和Zn虽有提升但是程度一般。 对比MAE的提升程度，依然是Cr的提升程度最高超过20%，Zn和Pb次之，而Ni和Cu效果一般。 对比RMSE的提升程度，则是Pb提升最高，Cr和Cu次之，Ni和Zn效果一般。 综合对比基体效应校正方程对于各元素的适用性，由高到低依次是Cr>Pb>Zn>Ni>Cu。

pXRF作为一种原位快速检测方法，其灵敏度、 准确度等条件固然不如ICP-MS等传统测试手段，但是他的便携性、 快速足以抵消这些缺点，同时可以发现，在通过选取较为干燥的近地表土壤和利用方程校正这两种方法，减弱含水率和基体效应这两个影响测试的主要因素后，pXRF的原位快速检测方法就综合成本和质量而言，是一种非常高效实用的方法。

2.3 对应分析

通过对元素和校区进行对应分析得到的对称归一化分布图(图3)，研究不同元素及校区之间的关系。 对称归一化分布图联合显示了行和列的坐标，可以更好地看到它们之间的距离。 维度1为行坐标，代表的变量是不同元素，描述了74.7%的惯性比例，维度2为列坐标，代表的变量是不同校区，描述了13.0%的惯性比例。 行距和列距是相应轮廓之间的近似卡方距离。 每个分类变量都以点方式显示在维空间中，绿色圆圈用于绘制元素，蓝色圆圈用于绘制校区。 原点表示平均分布的中心，而远离原点的点表示类别的影响更大。 这两个变量彼此接近，表明分布相似。 距离越近，相关性越强； 否则，关联性会减弱。

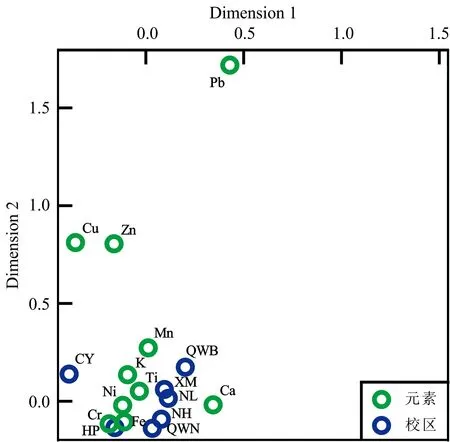
图3 通过对应分析得到的对称归一化分布图Fig.3 The symmetrical normalization distributionmap obtained by correspondence analysis

可以看见，样本点分布在所有四个象限内，呈散落式分布。 大部分点环绕在原点四周，仅有Cu，Zn和Pb游离在外。 观察各重金属元素与各常量元素间的相关性，发现各元素的基体效应校正效果，与该元素与其影响元素间的距离成正比，元素校正效果越好，元素间距离则越近。 其中以Cr和Fe尤为明显，甚至于两个元素点已经出现部分重合。 观察各元素与校区间相关性，未发现有明显的关联，同时也可以证明基体效应校正规律为重金属测试过程中的普便规律，与所处校区无关。

3 结 论

(1)经过基体效应校正法处理后，pXRF对Cr，Ni，Cu，Mn和Zn的定量测试数据质量提高，优于传统线性回归法。

(2)基体效应校正法对重金属元素的适用性是Cr>Pb>Zn>Ni>Cu。

(3)对应分析作为一种能够反映多维数据维度与维度之间关系的分析方法，用来探究多个变量间相关性是一种可行而有效的手段。