基于非线性光谱字典学习的单幅RGB图像光谱重建方法研究

左 楚，谢德红，万晓霞

1. 南京林业大学轻工与食品学院，江苏 南京 210037 2. 南京林业大学信息科学技术学院，江苏 南京 210037 3. 武汉大学，湖北省文物颜色信息数字化与虚拟再现工程研究中心，湖北 武汉 430079

引 言

光谱反射率因维度高、 与光源、 设备无关，并能较全面、 真实、 客观地描述颜色、 物质内部化学构成等信息[1]，被广泛地应用于颜色和物质分析[2-3]、 病症分析与判断[4]、 地质地貌的识别[5-6]。 目前，光谱图像常见获取方法有： 光谱相机[7]、 装备宽带滤光片或窄带光源的普通相机[8-9]。 光谱相机装备简单，但价格昂贵、 且所获光谱图像空间分辨率低； 装备宽带滤光片或窄带光源的普通相机较复杂、 难携带且不易推广使用。 因此，近些年利用单幅RGB图像直接重建光谱图像成为一个重要研究课题。

通常，光谱图像中光谱反射率维数远大于RGB图像中RGB值维数，直接利用伪逆方法重建光谱反射率病态问题严重，易产生较大重建误差[10]。 针对此问题，现有方法分为两类： 一类归为间接重建，一类归为直接重建。 间接重建方法认为像素的光谱反射率与RGB值在各自数据空间中的权重具有某种特定关系(如相等)。 基于此，间接重建方法从理论上回避了上述病态问题。 如，Chou等[11]在自然邻域插值算法[12]的思想上，构建了光谱反射率与RGB值在各自数据空间插值权重相等的假设前提，并在此前提下利用Voronoi网络重建了光谱反射率。 此方法有效地回避了三对多重建的病态问题，但须测试样本与训练样本的光谱数据特征相似、 且光谱反射率随波长均变化平缓[13]。 现实生活中，许多物质(如果荧光颜料)颜色鲜艳、 且光谱反射率随波长变化剧烈、 甚至存在窄波带波峰或波谷。 Arad等[14]提出了基于稀疏表示的重建方法(即SR_SR方法)，该方法先利用K-SVD分别训练样本的光谱反射率数据与RGB数据，得光谱和RGB两稀疏字典、 以及两个字典之间的映射矩阵，再依据两字典及两字典之间的关系重建了光谱反射率。 此方法虽缓解了对光谱反射率曲线的要求，但重建效果仍依赖于字典学习方法、 以及测试样本集与训练样本集的数据特征相似程度。

依据色度学原理，光谱反射率数据与RGB数据之间存在一个固有映射方程，如式(1)。 直接重建方法为缓解反演此方程病态问题的方法。 基于主成分分析法(principal component analysis，PCA)重建方法[15-19]为典型的直接重建方法，它假设任意颜色的光谱反射率均可由少数固有光谱征向量(即低维光谱字典)线性组成。 预先利用PCA获得低维光谱字典后，RGB数据与光谱反射率数据之间的反演问题则转变为RGB数据与光谱特征向量系数之间的反演问题。 因此，相对伪逆方法，该方法降低了求解的维数、 改善了病态状况，提高了光谱反射率的重建精度。 实际上，该方法能否有效降低求解维数在很大程度上依赖于光谱字典学习方法。 PCA只适用于线性数据，所获光谱字典难以低维表示非线性数据[20-23]。 Marjan[23]针对非线性光谱反射率数据，提出利用非线性主成分分析法(nonlinear principal component analysis，NLPCA)训练光谱字典。 此NLPCA[24]是一个基于优化方程的自联想神经网络模型。 在NLPCA的神经网络框架中，非线性传递函数可使获得地特征向量(或低维字典)切合数据的非线性特征，但也易使优化方程在求解过程中局部收敛、 而难获得全局最优解，最终影响光谱重建精度。

鉴于此，本文提出一种基于非线性光谱字典学习的非线性重建方法。 为了适应光谱反射率数据的线性或非线性特征，该方法首先通过改进传统NLPCA的优化方程，以适应于光谱反射率数据的线性或非线性特征，从而获得精度高、 稳定性好的低维光谱字典，再在此光谱字典基础上利用阻尼高斯牛顿法结合截断奇异值分解的正则化方法缓解该非线性反演的病态问题，以实现精度高、 稳定性好的光谱图像重建。

1 光谱直接重建框架

图像RGB数据与光谱反射率数据之间的映射方程如式(1)

(1)

式(1)中，pr(m)，pg(m)和pb(m)分别为第m个像素点的RGB数据、 且m=1, …,M，M为图像总的像素数，E(λn)为光源的光谱功率分布，sr(λn)，sg(λn)和sb(λn)分别为RGB三个光谱响应曲线，r(λn,m)为第m像素、 第n波段数的波长λn处的光谱反射率，N为可见光光谱范围内光谱反射率波段数。 由此，映射方程可进一步表示为

p=Ar

(2)

p=Af(D,u)

(3)

式(3)中，D∈RN×K表示低维光谱字典，u∈RK×1为系数向量，K为系数向量的维数，且K≪N。r=f(D,u)为光谱低维表达，f(·)表示线性或非线性光谱表达函数，若f(·)是线性的，光谱表达可为r=Du，且式(3)可写作式(4)

p=f(AD,u)

(4)

依据定理[25]，式(4)所求系数向量u的维数为K。 式(4)中，AD∈RN×K为N×K矩阵，其秩为rank(AD)≤min(N,K)=K。 若矩阵AD的秩等于K，则式(4)存在u的唯一解。 在此情况下，K越接近3，越有利用于缓解u反演的病态，但光谱表达精度越低。 在本文中，为了平衡光谱字典D准确表达原光谱反射率数据与降低式(4)反演的病态问题，除了f(·)线性或非线性自适应于训练光谱反射率数据外，K的取值一般远小于N且大于等于3，本文K取6。 此外，式中A∈R3×N非方阵，式(2)方程求解一般需乘以AT，转换为方阵ATA∈RN×N，即

ATp=ATAr

(5)

鉴于此，本文光谱图像重建框架如图1所示： 首先，选取光谱反射率数据作为光谱训练数据集，并利用本文所提光谱字典学习方法获得低维光谱字典与光谱表达函数，再利用阻尼高斯牛顿法结合截断奇异值分解的正则化法，获得单幅RGB图像的光谱图像。

2 光谱字典学习

2.1 基于NLPCA的光谱字典学习方法

鉴于上文所述，NLPCA[24]作为PCA的非线性扩展，被用以训练低维光谱字典(即固有光谱特征向量组)，获得了一定效果。 NLPCA是基于五个层结构的自联想人工神经网络的一种特征向量提取方法，其优化求解方程如式(6)和式(7)

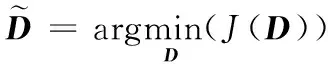
(6)

(7)

(8)

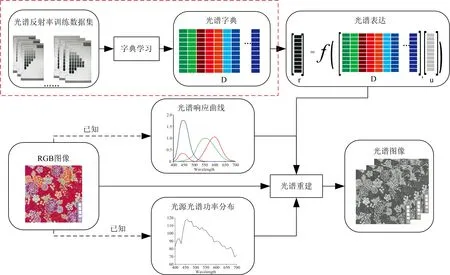
图1 本文光谱重建框架Fig.1 Overview of our proposed spectral reconstruction method

h(D)=f3(w(D)D+b(D))

(9)

式(9)中，传递函数f3(·)表示在神经网络框架下将光谱字典D映射成h(D)的过程。 光谱字典的公式为式(10)

(10)

式(10)中，传递函数f2(·)表示在神经网络框架下将隐含层神经元h(r)映射成光谱字典D的过程。 隐含层神经元h(r)的公式为式(11)

h(r)=f1(W(r)r+b(r))

(11)

2.2 基于改进NLPCA的光谱字典学习

PCA是NLPCA的特殊线性形式，即当上述优化方程中传递函数为恒定函数时，NLPCA则等同于PCA。 因此，在NLPCA的神经网络框架中，传递函数的非线性化可使获得的特征向量更切合非线性化特征的数据，但也易使优化方程在局部最小收敛，而难以获得全局最优。 本文将在NLPAC的基础上，在优化方程中添加正则化项，用以约束非线性传递函数，避免导致过度非线性化，以获得最优光谱字典。

如上所述，f1(·)和f3(·)采用是双曲正切函数，即f1(x)=f3(x)=(ex-e-x)/(ex+e-x)。 当其函数自变量x在某个范围内(如x∈(-L,L))时，若权重值w太小，传递函数趋于线性(即f1(wx)=f3(wx)≈wx)，获得的特征向量则难以切合数据非线性特征； 若权重值w太大，传递函数趋于一个阶梯函数，优化方程则可能在局部最小收敛。 因此，本文在式(7)优化方程的基础上，约束权重W(r)和W(D)，避免产生较大权重值，以有效控制非线性程度，使所得特征向量更切合训练数据特征、 且解趋于全局最优。 改进地优化方程如式(12)

(12)

式(12)中，‖·‖2表示l2范数，μ>0为正则化参数。 依据优化方法分析[26]，μ值越大，权重矩阵W(r)和W(D)元素值则越小，非线性程度则越低； 但若μ值过大，权重矩阵的元素值则均趋于0，式(12)优化方程则等同于式(7)。

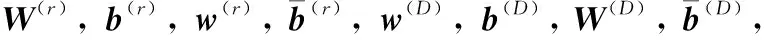
3 非线性光谱重建

由上所述，通过一组训练光谱数据集获得低维光谱字典D，并依据式(4)的光谱表达函数，建立RGB数据p与其光谱反射率数据r在光谱字典D下的系数向量u的求解优化方程，如式(13)

(13)

式(13)中，u的维数为K，远小于光谱r维数(即K≪N)，但仍高于维数p(即K>3)。 因此，式(13)的求解仍然面临着病态非线性数据反演问题。 本文将采用阻尼高斯-牛顿法[27]对相关系数矩阵u进行求解，并结合截断奇异值分解[28]的正则化方法以缓解该非线性反演的病态问题[29]。

令h(u)=p-f(AD,u)，式(13)则为

(14)

利用高斯牛顿法解决此最小二乘问题，则迭代公式为

h(uk+1)≃h(uk)+J(uk)sk

(15)

式(15)中，下标k表示迭代次数，uk+1=uk+sk，J(u)为h(u)的雅可比行列式，即

(16)

在每次迭代k中，sk求解优化方程如式(17)

(17)

式(17)中，Jk为J(uk)(雅可比行列式)或有限差分近似计算获得。 鉴于J(uk)计算过于复杂性，本文采用有限差分近似表示如式(18)

(18)

式(18)优化方程的最小二乘法求解可得如式(19)表示

(Jk)T(Jks+h(uk))=0

(19)

式(19)中，上标T表示矩阵转矩。 由式(19)可得迭代公式如式(20)

uk+1=uk+sk=uk-(Jk)′h(uk)

(20)

为了保证收敛性且避免陷入局部最小，引入一个阻尼因子α，获得阻尼高斯牛顿法的迭代公式如式(21)

uk+1=uk+αksk=uk-αk(Jk)′h(uk)

(21)

式(21)中，(Jk)′为Jk的Moore-Penrose伪逆。 阻尼因子α是通过结合Armijo-Goldstein原理[30]确定的。

如上所析，式(17)求解方程仍旧是病态的，本文将TSVD方法进行正则化处理，式(17)的优化方程更新如式(22)

(22)

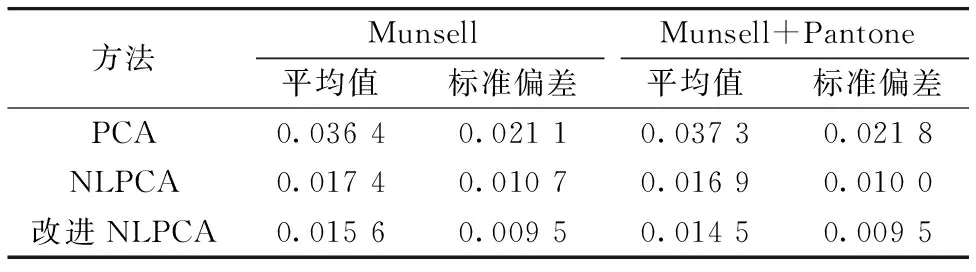
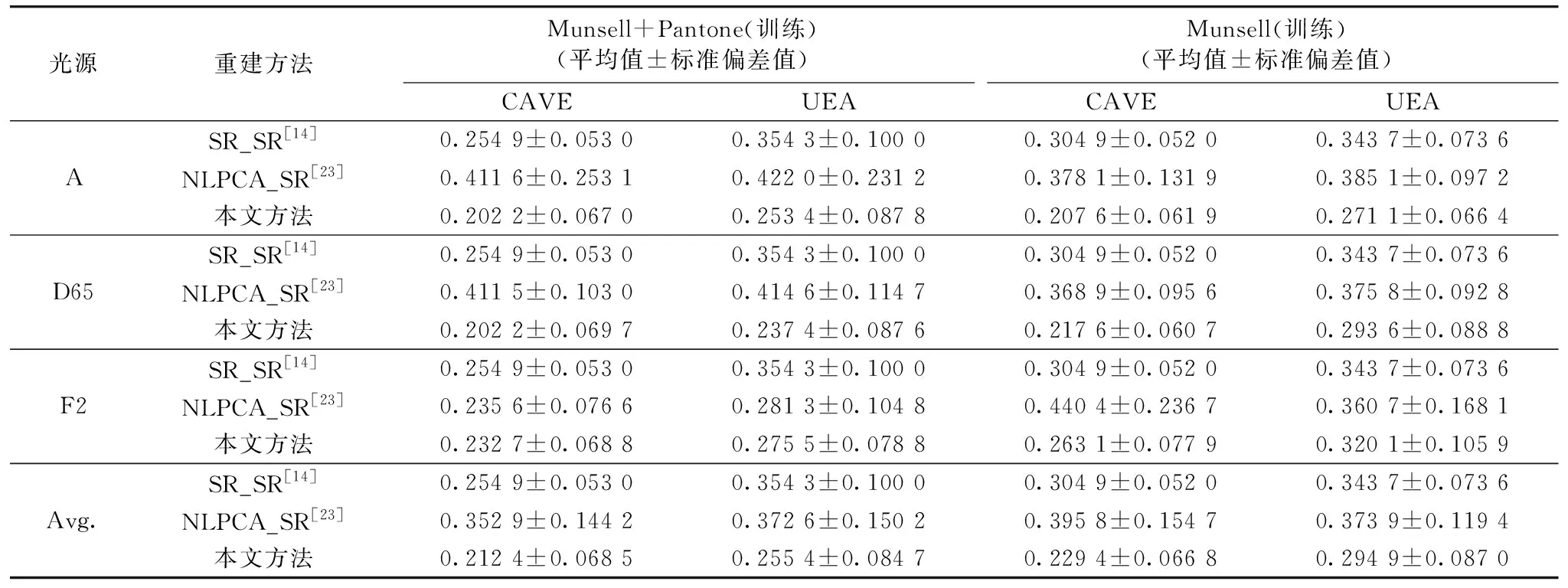
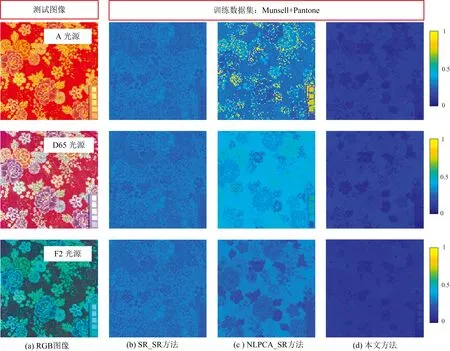
式(22)中，L∈Rt×K(t

Jk=CΣJZ-1,L=VΣLZ-1

(23)

式(23)中，C和V为正交矩阵，Z为非奇异矩阵，ΣJ和ΣL为对角矩阵，表示如式(24)

(24)

式(24)中，B=diag(b1, …,bt)，X=diag(x1, …,xt)。

由此，优化方程式(22)求解如式(25)

(25)

结合式(25)，更新式(21)为如式(26)正则化阻尼高斯-牛顿法公式

(26)

4 结果与讨论

为了验证方法的有效性，本文将分两个步骤进行评价： 光谱字典评价和光谱反射率重建评价。

4.1 光谱字典评价

如上所析，为了验证本文光谱字典学习方法对线性数据集和非线性数据集的适用性，本文选用了两个数据集： Munsell数据集和Munsell+Pantone数据集。 Munsell数据集的样本来源于Munsell颜色书[21]，包含1269个样本，其样本的颜色均匀分布在可见颜色空间[如图2(a)]，且样本的光谱反射率随波长变化均比较平缓； Pantone数据集来源于Pantone荧光色卡FFN100[31]，包含21个样本，其样本均为荧光颜色、 非常鲜艳、 可扩大Munsell颜色书的色域[如图2(b)]，且样本的光谱反射率随波长变化较为剧烈。 由此，依据参考文献[23]，Munsell构成的光谱数据集具有线性特征，Munsell+Pantone构成光谱数据集具有非线性特征。 数据集中，光谱反射率采集仪器为美国X-Rite Ci64型号的分光光度计，测量范围为400～700 nm、 采样步长为10 nm。 与此同时，还将其与现有线性方法PCA[15]和非线性方法NLPCA[23]进行对比，并采用重建结果均方根差(root mean square error，RMSE)的平均值和标准偏差值验证方法的准确性和稳定性。

图2 训练光谱字典的光谱数据集在颜色空间的分布(a)： Munsell； (b)： Pantone+MunsellFig.2 The distribution of two data sets in color space from the spectral dataset for training the spectral dictionary(a)： Munsell； (b)： Pantone+Munsell

表1中的数据为PCA，NLPCA和本文改进NLPCA所得光谱字典重建光谱反射率与原测量光谱反射率之间均方根差的平均值和标准偏差值。 其中，RMSE平均值表征光谱字典重建光谱反射率的精度，RMSE标准偏差值表征谱字典重建光谱反射率的稳定性。 平均值越小，重建精度越高； 标准偏差值越小，重建地稳定性越好。 由此，从RMSE平均值看，本文改进NLPCA方法所得光谱字典重建的光谱反射率精度最高； 从RMSE标准偏差值看，本文改进NLPCA方法所得光谱字典重建的光谱反射率稳定性也好于PCA方法和NLPCA方法。 此外，表1给出了Munsell和Munsell+Pantone两个数据集的重建结果，且Munsell数据集是线性的、 Munsell+Pantone数据集是非线性的。 从这两个数据集的重建结果看，本文改进NLPCA方法所得光谱字典的重建效果仍旧优于其他两种方法。 由此，说明本文改进NLPCA方法对线性和非线性数据集均具有优势。

表1 不同训练集的重建光谱反射率RMSE结果Table 1 RMSE results of reconstructed spectralreflectance for different train sets

4.2 光谱重建评价

为了进一步评价所得光谱字典以及验证本文基于光谱字典的光谱重建方法，本文在获得上述光谱字典的基础上，从CAVE[32]和UEA[33]两个图像库中选择图像作为重建的测试数据，并将其重建结果与基于NLPCA重建方法(NLPCA_SR)[23]以及基于稀疏表示的重建方法(SR_SR)[14]进行比较。 CAVE[32]和UEA[33]图像库中分别包含32和23幅图，每幅图的光谱图像的波长范围为400～700 nm、 间隔10 nm。 为了对比NLPCA_SR重建方法与本文重建方法对光源的鲁棒性能，其测试RGB图像分别由其光谱图像在光源A、 D65和F2下通过式(1)所得。 其中，RGB三个光谱响应曲线为CIE1931 20视场的标准观察者。

表2中，训练数据集分别为上述的Munsell数据集和Munsell+Pantone数据集，光谱重建的测试数据集分别采用了CAVE和UEA图库中的图像； 比较方法选取了NLPCA_SR方法[23]和SR_SR方法[14]。 其中，NLPCA_SR方法为利用NLPCA[23]获得低维光谱字典后再利用本文光谱重建步骤所得，SR_SR方法[14]为一个优秀的单幅RGB图像重建光谱图像间接方法。 表2中数据为RGB图像的重建光谱反射率与原光谱图像的光谱反射率之间RMSE的平均值和标准偏差值，且每格数据中： ±号前数据表示平均值，±号后的数据表示标准偏差值。 从整体看，本文方法重建的RMSE平均值均最小，表明本文方法具有较好光谱重建精度； RMSE标准偏差值虽不全为最小值(有些略高于SR_SR方法的结果)，但仍明显低于同类NLPCA_SR方法的结果，此表明本文方法在稳定性上与SR_SR方法不分伯仲、 较之NLPCA_SR方法具有一定优势。

表2 不同光源下RGB图像重建光谱反射率图像的RMSE结果Table 2 RMSE results of the reconstructed spectral images from their RGB images under different illuminants

表2中，第一列与第三列(或第二列与第四列)的训练数据集不同、 测试数据集相同。 从一、 三列(或二、 四列)对比看，本文方法重建的RMSE平均值和标准偏差值均明显低于NLPCA_SR方法，且未随训练数据集的变化而出现明显变化。 本文方法与NLPCA_SR方法均属于直接类重建方法。 如上文所述，直接类重建方法的重建精度依赖于光谱字典表达测试数据集中光谱数据的准确性，而此准确性又依赖于光谱字典学习方法。 由此，对比结果表明： 本文改进NLPCA方法更优，获得的光谱字典表达训练数据集的准确率更高、 稳定性更好、 更有益于获得高精度重建光谱图像。

依据方程病态问题反演定义可知，病态状况越严重时，即使数据变化(如光源变化导致RGB数值变化)很小，反演结果(如重建的光谱反射率)差异却很大。 表2中，不同行表示不同光源(如A，D65和F2光源)下RGB图像重建光谱图像的结果。 理论上，不同光源下重建光谱图像差异性越大，重建方法的病态问题则越严重。 从行数据对比看，较之NLPCA_SR方法，本文方法重建光谱图像的RMSE平均值和标准偏差值受RGB值变化(即光源变化)的影响均较小，此现象验证了本文方法也可很好地缓解重建方程反演的病态问题； SR_SR方法基本不受光源变化的影响，验证了SR_SR方法在解决病态问题上有明显地优越性。 但是，在不同训练数据集与测试数据集组合下，SR_SR方法重建效果差异也同时验证了此方法对训练数据集与测试数据集相似性要求的局限性。

图3和图4显示了A、 D65和F2光源下RGB测试图像以及三种方法重建光谱图像与原获取光谱图像之间的光谱差图。 其中，测试图像来源于CAVE图像库，图3的训练数据集为Munsell，图4的训练数据集为Munsell+Pantone。 在光谱差图中，越接近深蓝色表示光谱差值越小、 越接近白色表示光谱差值越大。 在SR_SR方法所得光谱差图中，图中整个区域基本呈现蓝色，且此现象基本未随着光源变化而变化，表明该方法重建的光谱图像精度较高，且缓解病态问题效果较好，因而重建光谱图像不随测试图像光源的变化而变化； 在NLPCA_SR方法所得光谱差图中，图中大部分区域呈浅蓝色、 小部区域呈现黄色，且此现象随光源变化较大，表明NLPCA_SR方法重建的精度和稳定性均略差，且缓解病态问题效果也较差，因而重建光谱图像随测试图像光源变化较大； 在本文方法所得光谱差图中，图中整个区域基本呈深蓝色、 且该现象未随光源变化而变化，表明本文方法重建光谱图像的精度与稳定性均较优，且缓解病态问题效果较好，因而对测试图像的光源呈现了较好的鲁棒性。 此外，由图3与图4对比可见，本文方法在两组不同训练集下均可重建较好效果的光谱图像。

图3 不同光源下的RGB图像与重建光谱图像的光谱差图，重建光谱图像的训练数据集为MunsellFig.3 RGB images under different illuminats and residual error map between their reconstructed spectral images and their original captured spectral images, the training dataset of the reconstructed spectral images is Munsell

图4 不同光源下的RGB图像与重建光谱图像的光谱差图，重建光谱图像的训练数据集为Munsell+PantoneFig.4 RGB images under different illuminants and residual error map between their reconstructed spectral images and their original captured spectral images, the training dataset of the reconstructed spectral images is Munsell+Pantone

5 结 论

提出了一种基于非线性光谱字典学习的非线性重建方法实现单幅RGB图像重建光谱图像。 在此方法中，首先利用了改进的NLPCA方法从训练数据集中学习出一个光谱重建精度高、 稳定性好的低维光谱字典，并用此光谱字典缓解RGB图像重建光谱图像方程反演的病态问题，然后还利用了阻尼高斯牛顿法结合截断奇异值分解的正则化方法，进一步缓解基于光谱字典重建方程反演的病态问题，最终获得重建精度和稳定性较好的光谱图像。 通过不同训练光谱数据集以及不同测试图像库，并通过重建光谱图像与原光谱图像之间RMSE的平均值和标准偏差值验证了： 在重建精度和稳定性方面，本文方法较之现有两种典型方法，具有一定的优势； 通过不同光源下RGB图像重建光谱图像效果还验证了： 本文方法对RGB图像的光源具有较好鲁棒性能。