一种基于环境去耦模型的架空导线动态增容方法
彭瑞东, 邓红雷 ,彭向阳, 周迦琳,王锐, 曾衍淇,郭德明,刘刚
(1.华南理工大学 电力学院,广东 广州510641;2. 广东电网有限责任有限公司电力科学研究院,广东 广州 510080)
随着用电需求的急剧增加,用电负荷集中地区(如长江三角洲、珠江三角洲等区域)的电网“卡脖子”问题日益突出,提升输电线路的电能输送能力成为亟待解决的课题[1-3]。动态增容技术可在不突破现行电网规程下,挖掘现有输电线路潜在的电能输送能力,对动态增容技术开展研究具有重要的意义。
动态增容技术通过计算架空导线的动态载流量来评估导线隐性输送能力[4]。现有动态增容模型研究主要分为2类。第1类动态增容模型监测导线的状态,主要包括热路模型[5-6]、导线温度模型[7]、弧垂模型[8]、张力模型[9]等。这类模型对导线相关状态参数(温度、弧垂)进行监测,通常需要在导线安装相应的传感器[10-11]。一方面在导线上安装传感器需要停电进行操作,另一方面传感器后期的维护非常困难[12-13]。文献[14]中提及可以通过红外温度传感器进行导线温度的监测,但是测量结果易受导线表面状态和环境的干扰。 第2类动态增容模型是监测导线所处环境的气候模型,对风速、风向、日照强度、环境温度进行实时监测,从而实现导线动态增容的计算[15]。气候模型计算精度取决于环境传感器的测量精度,但户外长期使用的风速传感器、日照强度传感器精度较差,对动态增容计算的效果影响较大[16-17]。文献[18]基于一种与导线处于同环境条件下的等效换热装置,提出等效换热模型用于架空导线载流量的计算。研究结果表明,利用发热铝球的稳态温度可以准确地评估导线载流量。由于发热铝球达到温度稳态所需时间较长,并且难以判断是否达到温度稳态,因此其工程应用效果较差。
因此,迫切需要提出一种既不需要监测导线状态,也不需要测量风速、环境温度、日照强度等环境参数,还能够便于工程应用的动态增容模型。结合前期的研究工作,利用高温铝球自然降温过程的暂态热特性,提出环境去耦模型用于动态增容计算。在模型的建立中,定义环境热交换关联参数f表征高温铝球和导线与环境之间的热交换;其次利用最小二乘法确定参数f的最优表达式,免去风速、日照强度、环境温度等传感器的使用;最后设计并搭建环境模拟实验平台,模拟实际铝球装置的运行,并将模型的计算结果与IEEE Std 738-2012标准(以下简称IEEE标准)的计算结果进行对比,以验证所提环境去耦模型的正确性。
1 环境去耦模型的建立
1.1 环境去耦模型的原理
前期研究工作所提出的等效换热模型,建立了同一气象条件下的发热铝球稳态温度和导线对流热损耗之间的关联模型,可实现导线载流量的评估。本文所建立的环境去耦模型则是利用高温铝球自然降温的暂态热特性,在不需要监测风速、环境温度、日照强度的情况下,实现导线载流量的计算。结合图1介绍环境去耦模型的原理。

图1 环境去耦模型的原理
架空导线在运行过程中,自身产生了电流焦耳热,并与环境产生热交换,从而达到热平衡状态。导线载流量的计算本质就是在评估导线与环境之间热交换作用(包含辐射散热、对流散热、日照吸热)的大小。在高温铝球的自然降温过程中,高温铝球与环境之间同样存在热交换作用。由于导线和铝球位于同一气象环境条件下,两者辐射散热、对流散热、日照吸热之间具有一定的关联性,所建立的环境去耦模型即是对此进行分析,从而利用高温铝球的暂态热行为间接计算出导线的载流量。
1.2 环境去耦模型的建立
环境去耦模型的本质是分析导线与铝球与环境之间热交换的关联特性,而热平衡方程很好地表达了热交换的作用。因此,环境去耦模型的建立需要先对导线和铝球的热平衡方程进行分析。
1.2.1 导线热平衡方程
当导线运行达到稳态时,满足热平衡方程
I2R(Tc)=qr+qc-qs.
(1)
式中:I为导线运行时加载的电流,A;Tc为导线温度,℃;R(Tc)为单位长度导线在导线温度为Tc时的交流电阻,计算可参考文献[19],Ω/m;qs为单位长度导线的日照吸热功率,W/m;qc为单位长度导线的对流散热功率,W/m;qr为单位长度导线的辐射散热功率,W/m。
IEEE标准介绍了导线热平衡方程各项的计算[20]。qr计算式为
qr=πD0εcσ[(Tc+273 ℃)4-(Ta+273 ℃)4].
(2)
式中:D0为导线的线径,m;εc为导线表面的辐射率;σ为斯蒂芬-玻尔兹曼常数;Ta为环境温度,℃。
qs的计算式为
qs=αcQsD0.
(3)
式中:αc为导线表面对日照的吸收率,与导线表面的辐射率相等[20];Qs为日照辐射强度,W/m2。
qc按照对流形式的不同分成不同的表达式进行计算:
(4)
(5)
Kangle=1.194-cos(φ)+0.194cos(2φ)+
0.368sin(2φ).
(6)
式(4)—(6)中:qcn、qc1、qc2分别为自然对流、低风速、高风速的对流散热功率,W/m;ρf为空气密度,kg/m3;kf为空气热导率,W/(m•K);Rec为导线的雷诺数;μf为空气的动力粘度,kg/(m•s);Vw为当前环境的风速,m/s;Kangle为风向因子;φ为风向和导线轴向之间的夹角。
文献[18]的研究结果表明风向对导线载流量的影响程度较小。另外,由于湍流的作用,风向引起的导线载流量变化远低于理论计算值[21]。因此,在本文的分析过程中,均取垂直于导线的风向(φ=90°)进行计算,即Kangle=1。同时,自然对流可以等效为某种风速下的强迫对流作用结果,因此,对于导线对流散热计算式仅需要考虑qc1和qc2即可。IEEE标准中在不同风速下通过qc1和qc2计算所得的对流散热功率如图2所示,qc取qc1和qc2中的最大值。因此,直接将IEEE标准中的qc2作为导线对流散热功率的计算公式可以在某些较小的风速下取一个较为保守的对流散热功率,有利于对导线载流量的保守计算。因此,导线对流散热功率

图2 IEEE标准导线对流散热功率
(7)
当给定导线温度Tc为最高允许温度(70 ℃)时,通过式(1)及各分项可以得到导线载流量
(8)
1.2.2 铝球热平衡方程
由于导线载流量的计算过程中导线温度取最高运行允许温度(70 ℃),为了计算方便,对于铝球同样取温度Ts=70 ℃进行分析。在铝球高温自然降温的过程中,满足热平衡方程
(9)
式中:qcs为铝球的对流散热功率,W;qrs为铝球的辐射散热功率,W;qss为铝球的日照吸热功率,W;ms为铝球的质量,kg;Cps为铝球的比热容,J/(kg•K);t为时间,s。
在传热学[22]中同样介绍了铝球相关换热功率的计算,qrs计算满足
qrs=πl2εsσ[(Ts+273 ℃)4-(Tas+273 ℃)4].
(10)
式中:l为铝球的直径,m;εs为铝球表面辐射率;Tas为铝球环境温度,℃。
铝球对流散热功率qcs的计算要考虑不同的对流情况,计算一系列传热学特征数的值。本文对于铝球对流散热功率的计算也是通过传热学特征数进行确定,首先利用牛顿冷却公式可得
qcs=hπl2(Ts-Tas).
(11)
式中h为铝球的对流换热系数。在传热学中,对流换热系数h与一系列的特征数相关,对流换热形式不同(自然对流或者强迫对流),相应的特征值种类及关系式也不一样。铝球的自然对流可以等效为对应某个风速的强迫对流。因此,对于铝球的对流换热,可以统一采用强迫对流的形式进行处理。当外界流体为空气时,铝球的对流换热系数的计算如下所示[23]:
(12)
式中:kfs、ρfs、μfs分别为当前环境空气的热导率、密度、动力粘度;Res为铝球的雷诺数;Nu为努塞尔数。
铝球的对流换热功率
(13)
铝球日照吸热功率[18]
(14)
式中:αs为铝球表面对日照的吸收率;Qss为当前环境日照辐射强度,W/m2。
1.2.3 环境去耦模型的载流量计算
在导线和发热铝球的热平衡方程分析过程中可以发现,导线和发热铝球与环境的热交换均包含对流散热功率、辐射散热功率和日照吸热功率。因此,在环境去耦模型的建立过程中,定义环境热交换关联参数f表征导线和发热铝球与环境热交换之间的关联特性,即
(15)
结合式(8)、 (9)、(15),可以确定环境去耦模型的导线载流量
(16)
1.3 环境热交换关联参数f的计算
结合1.2节对环境热交换关联参数f中的各项分析,可得:
(17)
由于导线和铝球所处的外界环境条件相同,当导线和铝球的辐射率相等时,即:
(18)
在式(17)中则会出现:

(19)
文献[24]的研究结果表明,物体温度较低时,对流散热量通常远大于辐射散热量。因此,在f中分母和分子表达式中第1项的数值远大于后2项的代数和。因此,定义可变参数a,将式(17)环境热交换关联参数f表达式转化为
(20)
式中可变参数a的值与铝球的物性参数、导线的物性参数、环境温度、风速、日照强度相关。结合式(20)即可将环境热交换关联参数f简化为f′:
(21)
进一步建立f与f′的误差函数f-f′,当导线和铝球的物性参数确定时,通过输入不同的环境参数,利用最小二乘法确定最优的可变参数a使得误差函数f-f′的值最小。在本文的分析中,铝球的直径l=0.03 m,确定不同型号、不同辐射率的导线对应的可变参数a的最优结果见表1。

表1 不同导线的可变参数a最优结果
由表1可知,不同型号、不同辐射率对应的参数a的最优结果相差不大,因此可以将上述3种型号导线对应的可变参数a值确定为相同的值。结合表1的结果,当铝球的直径为0.03 m时,针对以上3种型号的导线对应的参数a的最优结果可以确定为a=0.73,由此,
(22)
则环境去耦模型的导线载流量
(23)
由式(23)可知,当导线的型号和铝球的直径确定后,环境去耦模型的导线载流量的计算所需要的参数为发热铝球在当前环境条件下的70 ℃的温度变化率。
1.4 环境热交换关联参数f的简化误差分析
1.3节对环境热交换关联参数f进行了简化分析,使得环境去耦模型在载流量计算过程中免去了风速、日照强度、环境温度。因此,有必要对于f的简化过程中的误差进行分析,进一步将误差表征在导线载流量Iamp的计算结果上。在本节的误差分析过程中所选取的导线型号为LGJ-240/30,辐射率为0.6;对于环境参数的选取参考了导线实际监测所得的环境参数范围[18]。
通过上述设置计算简化后参数f(即式(22)计算值)的计算值为19.98。在日照强度为0、500 W/m2、1 000 W/m2,不同风速和环境温度下的参数f的真实计算值(即式(17)计算值)和简化结果与真实结果的比值如图3所示。
从图3中可以看出,当外界环境条件发生改变时,参数f的简化误差也随之发生改变。在不同的外界环境条件下,参数f简化的相对误差结果在13%以内。这也说明了1.3节中对于可变参数a的寻优结果非常合适。因此,对于参数f的计算简化是可以被接受的。

图3 不同环境条件下参数f的简化误差分析
进一步引入误差因子δ表征载流量Iamp的误差δIamp与参数f的误差δf之间的关系,即:
(24)
结合式(23)消项得到
(25)
由式(25)可知,当f的简化误差为-10%~+12.5%时,对模型载流量带来的误差在-5.2%~+6.3%以内,能够被工程应用所接受。
2 环境去耦模型的实验验证
在第1章中介绍了环境去耦模型对导线载流量的计算方法,并对环境热交换关联参数f进行了简化分析。在本章中将搭建环境模拟实验平台,对铝球在不同环境条件的自然降温过程进行模拟。同时以LGJ-240/30型号的钢芯铝绞线为研究对象,利用所获得的铝球温度微分项,结合环境去耦模型对导线载流量进行计算。并引入相同环境条件下IEEE标准的计算结果,从而验证本文所提出的环境去耦模型载流量计算方法的正确性。
2.1 实验平台搭建
所搭建的环境模拟实验平台如图4所示。环境模拟实验平台主要设备包括:负压风机、转速控制台、热敏式风速检测仪、半导体散热器、温度传感器、发热铝球装置、温度记录仪、氙灯和相应的控制器以及数显式日照辐射计。该实验平台实现了风速和日照辐射强度的模拟。

1—散热风扇;2—长弧氙灯;3—热敏式风速检测仪;4—铝球;5—温度传感器;6—半导体散热器;7—负压风机;8—日照强度控制器;9—温度记录仪
首先按照第1章的建模要求设计并试制铝球。本次试制的铝球直径为0.03 m,铝球质量ms测量结果为0.040 4 kg。其中,提供热源的电阻丝放置在铝球的中心。铝球的底部设计有一根支撑杆,其作用是固定铝球的位置。为了尽可能保证铝球的温度分布与理想球体一致,支撑杆采用PEEK绝热材料制造。电阻丝的引线则是穿过支撑杆的内部并接入直流电源的两端。
对于风速的模拟主要通过负压风机和转速控制台实现。负压风机位于一个封闭循环的风洞内,转速控制台通过伺服电机控制负压风机的转速从而调节风洞内风速大小。热敏式风速检测仪(分辨率为0.01 m/s,精度为0.1 m/s)则是用于测量风速的大小。风机的转速与风速之间呈线性关系,如图5所示。风机等设备在运行过程中会产生热量,导致风洞内的环境温度升高。为了解决这个问题,风洞内还装有4台半导体散热器以保证风洞内的环境温度恒定。

图5 风机转速与风速之间的关系
通过长弧氙灯实现日照强度的模拟[25]。由于长弧氙灯在启动以前的常温下就有很高的气压,因此需要配备相应的触发器点燃氙灯。通过额定功率为1 000 W的开关电源提供稳定的大功率直流电源,调节电源的输出功率改变氙灯的发光强度来模拟日照强度的变化。并通过数显式日照辐射计对铝球所受的辐射强度进行监测。氙灯在工作的时候会产生较多的热量,因此配备2台风扇进行散热。
实验过程中,用于测量温度的温度传感器采用接触式的T型热电偶。环境温度的测量点如图4所示。铝球温度的测量点则是位于铝球的背风侧表面[18]。所有的热电偶连接至温度记录仪,实现数据的监测和记录。给铝球内的电阻丝加载一定功率使铝球温度到70 ℃后停止加热,接着让铝球在风洞内自然冷却。每0.5 s采集1次温度数据,从70 ℃开始,采集1 300个降温过程铝球暂态温度数据,用于后续计算。
2.2 基于实验结果的模型验证
环境温度在实验过程中存在小幅度的波动,取其平均值进行计算。通过调节不同风速和不同日照强度模拟铝球的自然降温热行为,获取不同条件下的铝球暂态降温温度数据。
将所有铝球暂态降温温度数据按照文献[26]提到的一阶电路全响应表达式拟合出铝球的温度函数表达式,如式(26)所示。对温度函数求导,从而对铝球温度为70 ℃下的温度微分项进行求解。
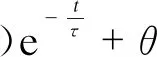
(26)
式中:θ(t)为铝球温度随时间变化的函数;θ(0+)为铝球的初始温度;θ(∞)为铝球的最终温度;τ为铝球的热时间常数。
图6所示为本次模拟实验中采集得到的不同环境条件下的铝球暂态温度数据。将图6中的暂态温度数据按照式(26)进行处理,对环境去耦模型求解。见表2不同实验条件下的环境去耦模型的载流量计算结果,并引入IEEE标准在同样环境条件下的计算结果进行对比。

图6 铝球温度数据采集结果
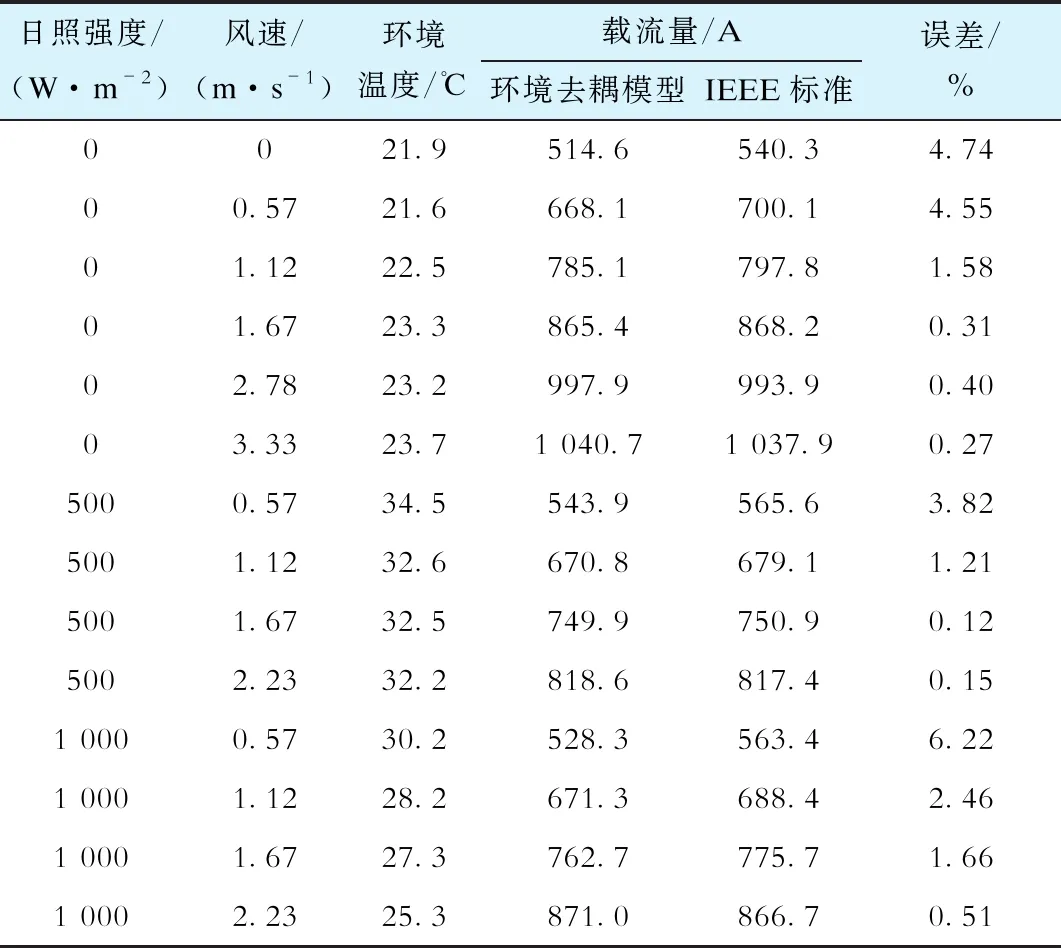
表2 环境去耦模型和IEEE标准的载流量计算结果对比
由表2可知,在不同环境条件下,环境去耦模型的载流量计算结果与IEEE标准结果较为接近,最大误差为-6.22%。从表2的误差数据可以发现,环境去耦模型相较于IEEE标准的载流量计算结果是一个保守的结果,并且风速越大,误差的绝对值越小。这是由于环境去耦模型中对于导线对流换热项qc采用的计算表达式为qc2的表达式,从而使得导线对流换热功率计算值相比实际对流换热功率计算值偏小。表3为上述实验环境参数下的导线对流散热功率的计算结果对比。在IEEE标准中对流散热功率qc计算取qc1和qc2的最大值,而本文所提的环境去耦模型在建立过程中直接采用qc2的计算结果。由表3可知,在风速较低时,qc2的计算结果要略小于qc;当风速增大一些后,qc的计算结果与qc2的计算结果又保持一致。所以在环境去耦模型的载流量计算中,当风速较低的时候,所采用的对流散热功率计算表达式相对IEEE标准是保守计算。所以模型的载流量计算结果在风速较低的时候相较IEEE标准会出现负误差,当风速变大时,该负误差便会消失。
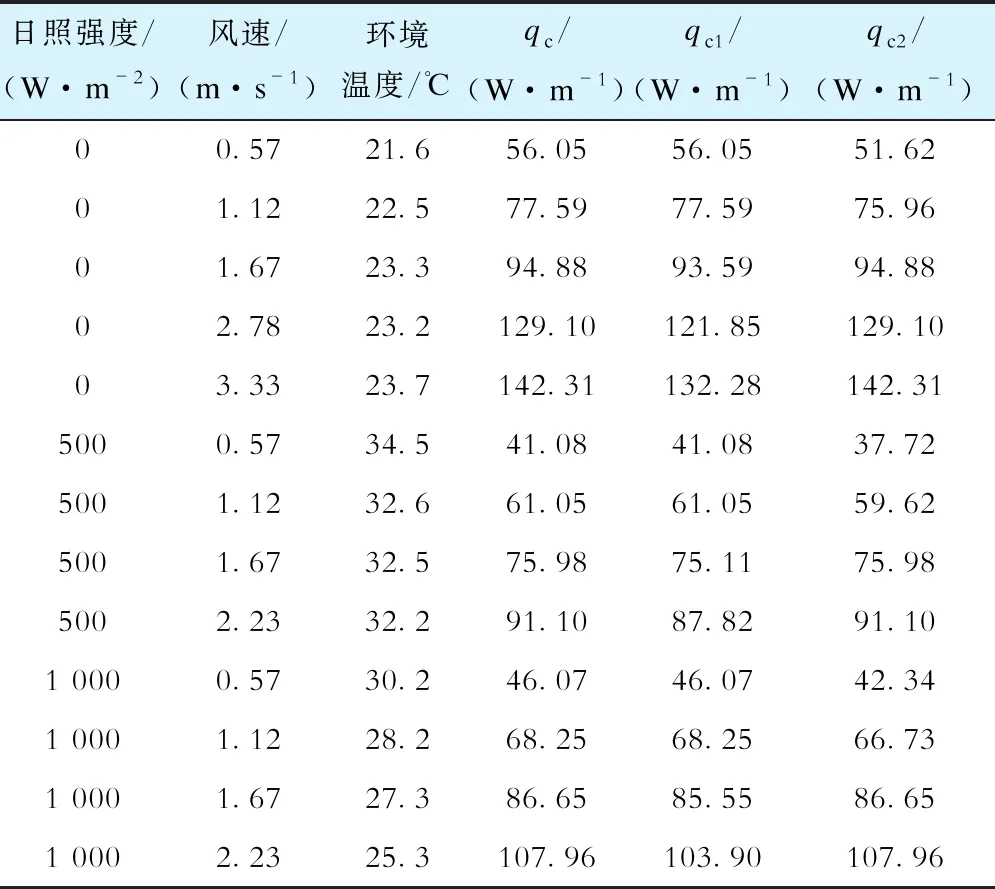
表3 基于环境参数的导线对流散热功率
因此,环境去耦模型配合等效换热装置的工作模式可以在不需要监测导线状态以及风速、环境温度、日照强度的前提下,仅获取铝球降温过程中在70 ℃下的温度变化率,实现架空导线载流量的准确评估。
3 结论
本文通过高温铝球自然降温的热行为,提出一种架空导线动态增容计算的环境去耦模型。所提模型通过铝球与环境之间的热交换关联了导线与环境之间的热交换,在不需要监测导线状态的同时也不需要监测风速、日照强度、环境温度就可以实现导线载流量的评估。本文研究工作的具体结论包括以下几点:
a)环境去耦模型的建立过程中,在低风速下对导线对流换热功率进行了保守计算,使得较低风速下环境去耦模型计算结果相较IEEE标准相对保守。
b)对环境去耦模型中的环境热交换关联参数f进行简化分析,并利用最小二乘法确定其最优化表达式,使得其计算仅与导线、铝球的几何参数相关。
c)在不同环境条件下,环境热交换关联参数f的简化结果相较真实结果的误差在13%以内。同时引入误差因子表征参数f的简化误差与模型载流量计算误差之间的关系,确定了参数f简化导致的模型载流量计算误差在6.3%以内。
d)通过搭建环境模拟实验平台模拟等效换热装置的运行,利用环境去耦模型实现导线载流量的计算。对比在不同环境条件下的模型计算结果与IEEE标准的计算结果,误差均不超过7%,从而验证了本文提出模型的正确性。

