基于BDS/INS紧组合的动对动相对导航算法

付希禹，孙永荣，吴 玲,2，曾庆化，刘建业

（1. 南京航空航天大学 自动化学院导航研究中心，南京 211106；2. 南京航空航天大学金城学院 机电工程与自动化学院，南京 211156）

相对导航是获取目标间相对关系的重要手段。传统的动态相对定位技术要求基准站精确位置已知且固定，导致使用场景受到较大限制[1]。基准站覆盖范围有限情况下，如空中加油、交会对接、无人机编队、舰载机着舰等，差分数据链将不再可靠，传统相对定位技术无法满足实际需求。动对动相对定位技术能够通过差分的方式得到两个移动目标之间相对位置关系，克服传统定位方法中基准站覆盖范围不足的问题[2]。北斗三号全球卫星导航系统（BeiDou Satellite Navigation System, BDS）已于2020年正式开通，摆脱了以往GPS技术受制于人的局面。因此，对于北斗导航系统的研究成为热门研究方向。

惯性导航系统（Inertial Navigation System, INS）是目前运用最多的自主式导航系统，具有短时精度高、更新率高、自主性强等特点。因此，BDS和INS组合导航系统可以实现优势互补[3,4]，在北斗卫星信号丢失、可观测数目不足时，仍可以保持高精度位置输出。文献[4]深入分析了单频多模RTK/MEMS紧组合在提高单频RTK定位性能方面的优势，并通过实验进行了性能验证；文献[5]在传统紧组合基础上，设计了一种基于高斯检验探测和改善卫星导航故障方法，在信号部分或完全暂停时，显示出良好的桥接能力；文献[6]在GPS/BDS/INS紧组合系统中提出一种改进多模型交互式滤波，减少动态模型不确定性带来的性能降低，最终实现分米级定位精度。文献[7]提出一种自适应鲁棒CKF用于GNSS/INS紧组合，抑制模型误差以提高定位精度；文献[8]通过在紧组合中引入RTSS和前后向组合平滑算法，提高相对及绝对定位精度，并通过跑车实验测试了性能。复杂环境下，卫星信号易受到遮挡，观测质量不佳，经常发生周跳，整周模糊度浮点精度不高，难以精确固定；而且移动基准站和流动站同时发生卫星信号丢失时，由于移动基准站无法提供位置信息，无法继续维持相对导航。

本文针对复杂场景下，卫星观测质量不佳、信号丢失时，BDS定位精度不高、无法连续定位的问题，结合BDS和INS系统特点，利用先验信息，提出了一种基于BDS/INS紧组合的动对动相对导航算法。

1 BDS/INS紧组合动对动相对导航模型

本文所提出的基于BDS/INS紧组合的动对动相对导航算法为基于动对动的双站相对导航系统，移动基准站处于运动状态。基于BDS/INS紧组合的动对动相对导航算法流程如图1所示。从算法结构上，优先采用基于多普勒的伪距信息平滑优化，移动基准站和流动站均采用紧组合信息融合方式。移动基准站通过单点伪距/伪距率的紧组合方式，提供移动基准站位置、速度、姿态信息。进一步地，对移动基准站与流动站同步观测，构成双差观测方程。观测量双差后消除或削弱大部分误差，如卫星钟差、接收机钟差等，简化系统状态误差模型。由惯导预测的位置和速度代替卫地距和卫地距变化率对伪距、伪距率方程线性化，从而构建流动站紧组合双差观测方程。移动基准站与流动站均进行信息融合，通过紧组合进行扩展卡尔曼滤波，获得系统状态的最优估计。最后，组合滤波结果分别对惯性器件误差实时校正，并解算两站之间的相对导航结果。

图1 基于BDS/INS紧组合的动对动相对导航算法流程Fig.1 Flowchart of kinematic-to-kinematic relative navigation algorithm based on BDS and INS tightly coupled

1.1 紧组合状态方程

若不考虑北斗卫星导航系统误差量，则系统状态模型由惯导误差模型及惯性传感器系统误差来描述。因此对捷联惯导构建姿态、速度、位置误差模型[5,6]。

式中，δ r、δv、ψ分别为位置误差、速度误差和姿态角误差，∇为加速度计误差，ε为陀螺漂移，ωie为地球系相对于惯性系的地球自转角速率在地理系上的投影，ωen为地理系相对于地球系的地球自转角速率在地理系上的投影。

因此紧组合状态方程为：

式中，X(t)为状态向量，X=[(δr)T(δv)TψTεT∇T]T，F(t)为状态转移矩阵，G(t)为系统噪声驱动矩阵，W(t)为系统噪声阵。

1.2 紧组合观测方程

1.2.1 基于多普勒的伪距信息平滑方法

载波相位平滑伪距是提高伪距观测值精度的常用方法，当周跳较少或不发生周跳时，可有效提高伪距精度。但处于遮挡环境时，卫星观测质量差，导航信号发生失锁，平滑器则需不断重置，影响载波平滑伪距的精度。相关研究表明，当周跳发生时，载波相位平滑伪距的精度明显降低，多普勒无模糊度影响，因此在复杂环境下对伪距的平滑比载波相位更加准确[9,10]。

基于Hatch滤波，载波相位平滑伪距算法为[11]：

式中，M为平滑时间常数，为k时刻平滑后伪距，Pk、φk分别为k时刻伪距和载波相位，λ为北斗B1频段波长。式(3)可实现载波相位对伪距平滑，在一定程度上提高伪距精度。多普勒频移是观测文件中的观测量，具有良好的观测精度，不因载波相位发生周跳而产生变化。对多普勒频移积分是对多普勒频移造成载波相位变化量的叠加，其在数值上表现为载波相位的变化量[12]，因此用多普勒频移观测值代替载波相位差分，即：

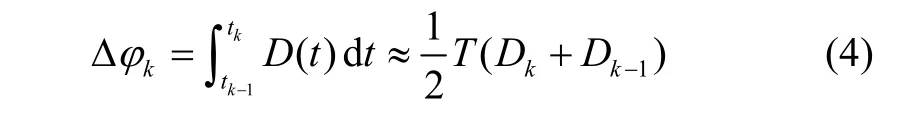
式中，T为历元间隔。将式(4)代入式(3)，则多普勒平滑伪距公式为：

1.2.2 动态对动态相对导航观测方程

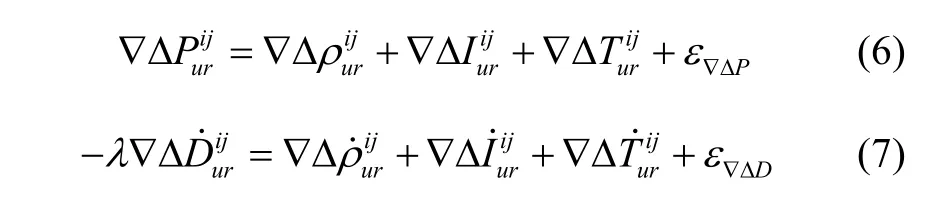
式中，∇Δ为双差算子，P和D为伪距及多普勒，ρ和ρ˙为惯性预测卫地距及卫地距变化率，I和T分别为电离层误差和对流层误差，ε∇ΔP和ε∇ΔD为噪声项。站星双差可消除卫星钟差及接收机钟差，短基线情形下，可显著消除大气延时误差，有效提高观测精度[6]。代入卫地距在INS预测位置(xu0,yu0,zu0)、预测速度(x˙u0,y˙u0,z˙u0)一阶泰勒展开式，忽略大气延迟，可得动对动的伪距、多普勒双差观测方程：

式中，Δl、Δm、Δn为方向矢量差。传统RTK定位基准站固定且精确位置已知，移动基准站情形下并不存在此前提。GNSS相对定位中对起算点坐标的要求并不高，有时误差可超过10 m[2]。对于紧组合后的移动基准站的输出，满足以上要求。

综合式(8)(9)，需要注意的是，由于状态方程是在地理坐标系下进行建模，进一步将状态量δ r、δv转换到地心地固坐标系（ECEF）下。若双站同时观测M个共视卫星，则可得到2(M-1)个方程，联立构成BDS/INS紧组合动对动相对导航观测方程：

式中，K为方向向量构成的设计矩阵。为地理系到地球系的坐标系转换矩阵。

1.3 基于扩展卡尔曼滤波的卫星/惯性信息融合

对于上述动对动量测信息，卫星/惯性量测信息融合通过扩展卡尔曼滤波（Extended Kalman Filter, EKF）进行参数估计。优先将状态方程离散化，随后进入组合导航滤波计算。滤波方程的系统噪声协方差阵通过对惯性器件转台标定后确定。顾及观测质量，量测协方差阵通过卫星高度角进行建模：

式中，Kk为增益矩阵，Xk+和Pk+为k时刻后验状态向量和协方差矩阵，Zk为观测矩阵，Hk为量测矩阵，Rk为量测噪声矩阵。通过如式(12)(13)所示的滤波过程即可完成单历元推算。对于紧组合，当出现高楼、树木等卫星信号遮挡情况时，卫星数减少，观测方程维数将下降，但仍可进行滤波计算。数据融合后，通过流动站与移动基准站的位置速度作差，进一步得到相对导航结果。

2 实验验证与分析

为验证本文算法有效性，搭建了如图2所示BDS/INS的动态对动态实验平台，基于该平台开展车载实验。实验地点为位于江苏省南京市宁丹大道的城市环境，城市道路较为开阔，有效数据采集时间约为30 min，运动轨迹如图3中黄色曲线所示。

图2 车载实验平台及场景Fig.2 Experiment platform and scene

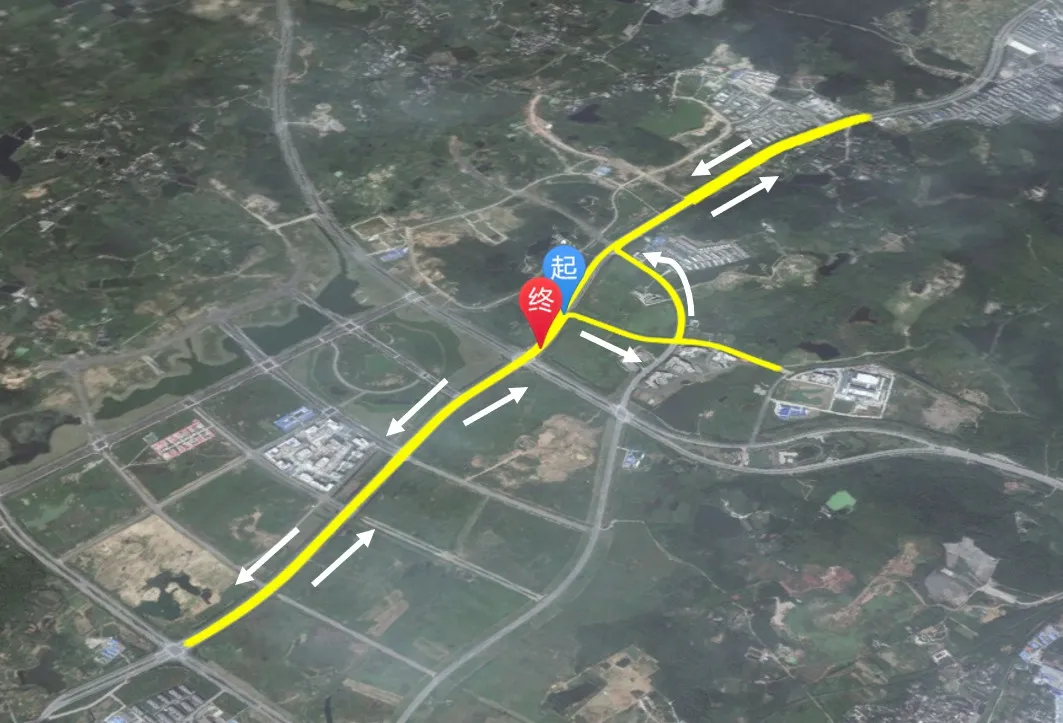
图3 实验轨迹图Fig.3 Trajectory of experiment

实验平台惯性设备为荷兰XSENS公司出品的MTI-G-700型惯性传感器，标称陀螺仪零偏稳定性为10 º/h，加速度计精度40 μg。GNSS接收机为NovAtel OEM6板卡授时导航接收机，GNSS天线吸附在车顶。卫星/惯性采样频率分别为200 Hz和1 Hz。两部车载测量系统分别标记为移动基准站和流动站，经测量卫星/惯性空间杆臂误差lb=[-0.2,0,0.14]Tm 并校正。移动基准站及流动站速度及其基线长度变化如图4-5所示。

图4 移动基准站速度及基线长Fig.4 Velocity and baseline length of moving base station

图5 流动站速度及基线长Fig.5 Velocity and baseline length of rover station

行驶过程中两车保持动态对动态运动状态，卫星截止高度角为15 º，可见卫星数量及PDOP变化情况如图6所示。从图中可以看出，实验过程中，截止高度角为15 º情况下，可见北斗卫星数量保持在15颗左右，平均卫星数量14.6颗，平均PDOP 1.60；部分历元出现树木遮挡，卫星数量下降至11-13颗左右，整体观测质量较好。

图6 可见卫星数量及PDOPFig.6 Satellite visibility and PDOP

为对本文算法进行分析，车载系统同时搭载了千寻网络RTK，并将定位及测速结果作为参考基准，整周模糊度正确固定时，可输出cm级定位结果。图7-8为采用两种相对导航方案统计得到的相对导航结果，蓝色标识为基于伪距/伪距率差分的卫星相对导航（方案1，SRN），红色标识为本文BDS/INS相对导航算法（方案2，TCRN）。

图7 SRN/TCRN相对位置误差Fig.7 SRN/TCRN relative position errors

图8 SRN/TCRN相对速度误差Fig.8 SRN/TCRN relative velocity errors

进一步地，对上述两种方案的E/N/U三个方向的相对位置、相对速度误差平均值、均方根误差（Root Mean Square, RMS）、最大值、最小值进行了统计分析，如表1所示。

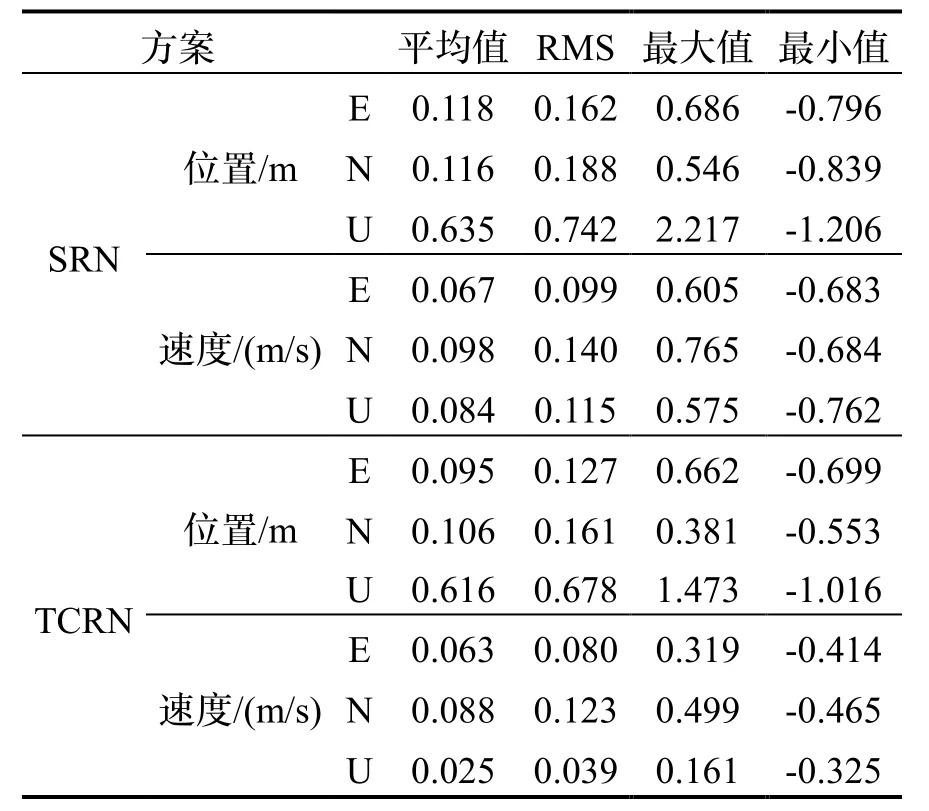
表1 SRN/TCRN相对导航误差表Tab.1 SRN/TCRN relative navigation errors

综合上述结果可以发现，基于伪距/伪距率差分的相对导航由于消除或削弱了星钟误差、大气延迟的影响，相对位置及相对速度精度达分米级。同时，由于惯性参与信息融合滤波，基于BDS/INS紧组合的动对动相对导航算法中有效抑制了伪距差分算法中包含的噪声，相对位置、相对速度误差曲线更加平滑，性能得到显著改善。具体而言，以RMS误差为例，相对位置E、N、U方向误差分别从0.162 m、0.188 m、0.742 m降至0.127 m、0.161 m、0.678 m，本文所提出的算法在相对位置精度分别提升了21.6%、14.4%和8.63%；相对速度E、N、U方向误差分别从0.099 m/s、0.140 m/s、0.115 m/s降至0.080 m/s、0.123 m/s、0.039 m/s，相对速度精度分别提升了19.2%、12.1%、66.2%。通过BDS和INS数据融合，相对导航系统可实现优势互补，这一结果验证了紧组合在相对导航上的精度优势。

为进一步分析动对动相对导航算法在卫星观测质量不佳、信号丢失时的性能，历元时间内分别设置5 s、10 s、20 s、30 s卫星中断，模拟信号失锁中断场景，以验证所提方法有效性。表2反映了在信号中断时，本文方法的RMS误差。

表2 BDS中断条件下导航性能Tab.2 Navigation performance in adverse BDS condition

显然，BDS信号中断观测条件下，由于无法获得观测信息进行差分解算，依赖卫星的相对定位、测速算法将不再可用，相对位置及相对速度信息无法获得，这对应用于动对动的场景，如空中加油，将产生极大的风险。通过分析可知，紧组合出现了随时间发散的特性，但由于惯导具有短时精度高的特性，可保持一定程度的相对导航能力，保证系统连续的相对导航信息输出，但限于IMU精度，其能力有一定上限。从上述实验分析中可以看出，本文算法在以上场景中，能较好的保持相对导航能力，有效提升了动对动相对导航的稳定性和可靠性。

3 结 论

为改善卫星观测质量不佳及信号丢失时，BDS定位精度不高、无法连续定位的问题，结合BDS和INS系统特点，提出了一种基于BDS/INS紧组合的动对动相对导航算法。文中分析构建了捷联惯导系统误差模型；研究了多普勒平滑伪距算法；构建了相对导航观测模型，并通过紧组合EKF滤波数据融合，最终解算获得相对导航结果。通过车载实测实验，结果表明，相比于卫星导航算法，紧组合在相对导航上具有一定的精度优势。当卫星信号受到遮挡中断时，基于BDS/INS紧组合的动对动相对导航算法能够继续保持相对导航能力，从而有效提升了动对动相对导航的稳定性和可靠性。