基于改进灰狼算法优化的支持向量机锌耗预测

张佳琦， 顾幸生

（ 华东理工大学能源化工过程智能制造教育部重点实验室，上海 200237）

锌锭是生产镀锌板的主要原料之一，广泛用于汽车、建筑、船舶、轻工等行业。锌锭的消耗不仅与合同订单相关，而且与目标产能和产品结构等相关。由于锌层控制精度低，再加上生产中不可避免的锌渣，锌锭消耗波动较大，导致炼钢厂的锌锭需求量浮动。在供应链的信息传递过程中，需求预测的不准确性会被逐渐放大，势必对物料采购计划和库存管理造成影响，因此准确的锌锭需求预测能指导钢铁企业进行物料采购优化，做出正确的生产经营决策。

物料需求预测往往受合同订单、销售计划、生产能力等多重因素影响，呈现出样本量小且变化范围大的特点，其非平稳性和非线性使需求预测问题的难度增大。为提高物料需求预测的精确度，使得需求预测行之有效，学者们进行了大量研究，采用的建模方法主要分为时间序列预测、机器学习预测和混合模型预测。文献[1]构建了灰色理论与指数平滑的需求预测综合模型对汽车制造业的车型需求量进行了预测。文献[2]运用灰色关联分析和支持向量机回归相结合的方法对备件库存消耗进行预测。文献[3]运用粗糙集和熵权法，改进了粒子群优化的搜索方式和最小二乘支持向量机的加权方式，建立了基于粗糙集和熵权以及改进支持向量机的组合预测模型，用于导弹备件消耗预测。文献[4]针对非平稳、非线性的企业实际物料需求时间序列，提出了基于经验模态分解及粒子群算法优化的最小二乘支持向量机回归的物料需求组合预测模型。文献[5]基于泊松分布建立物料需求时间模型，对时间序列进行相空间重构后，利用遗传算法优化BP神经网络，进行汽车物料预测。

基于统计学理论建立的支持向量机回归（SVR）模型在处理非线性、高维问题时具有较好的鲁棒性和泛化能力，目前已被广泛应用于小样本回归，如金融领域预测、交通流量预测和电力负荷预测等[6-8]。在SVR模型中，合理设置惩罚因子、核函数参数是提升模型预测能力的关键所在。现阶段常用的参数选择方法主要有3种：（1）试凑法，其对样本数据质量和使用者的经验有较大的依赖性；（2）网格搜索法（Grid Search, GS）[9]，其将待搜索参数在给定的空间范围内划分成网格，通过遍历网格中所有的点来寻优，该方法实现简单但较为费时且寻优能力有限，容易错失全局最优解；（3）智能算法，包括粒子群优化（PSO）算法[10]、遗传（GA）算法[11]、人工蜂群(ABC)算法[12]、布谷鸟搜索(CS)算法[13]。

灰狼优化[14]（Grey Wolf Optimization，GWO）算法是一种受狼群狩猎启发的群智能优化算法，具有参数少、易实现的特点，比PSO、GA、DE等算法稳定性更强，收敛速度更快，在解决复杂优化问题时表现出了良好的性能，如特征选择[15]、神经网络优化[16]、路径规划[17]、流水车间调度问题[18]等。但GWO算法同样存在易陷入搜索停滞状态的缺陷，对此国内外已有学者展开了研究。文献[19]将动态进化种群融入GWO以提高GWO的局部探索能力；文献[20]提出了一种基于Powell局部优化方法的扩展灰狼算法用于数据聚类；文献[21]改进了收敛因子策略并引入动态权重策略来优化灰狼算法的性能；文献[22]结合差分进化和灰狼算法的优势，提出了一种混合算法用于三维芯片测试，进一步平衡算法的勘探和开采能力；文献[23]提出了一种基于混沌原理和精英反向学习策略的混合灰狼优化算法，用于解决高维函数优化问题；文献[24]嵌入一种最优最差反向学习策略和一种动态随机差分变异算子来改进灰狼优化算法用于提升聚类优化性能；文献[25]提出了灰狼优化与蝗虫优化的混合算法以解决文本挖掘问题。

针对传统灰狼算法收敛快、易早熟的问题，本文在灰狼算法基础上引入 Tent 混沌序列初始化种群，采用控制参数的自适应调整策略，并融合差分进化思想，提出了改进的灰狼优化算法（IGWO）进行SVR参数优化（IGWO-SVR）。以某钢厂某机组的锌锭生产实际数据为例，建立IGWO-SVR锌耗预测模型，以提高锌锭需求预测的效率和精度。

1 支持向量机

支持向量机（SVM）[26-27]是一种建立于统计学习理论基础上的新型数据挖掘方法，在高维、非线性等问题中有着良好的表现。SVR是SVM的衍生模型，其基本思想是用一个非线性变换将原始样本数据映射到高维空间再进行线性回归求解，旨在寻找一个最优超平面，使得所有样本离该最优超平面的距离最小。选择稀疏性好、泛化能力强的 ε -支持向量机回归作为损失函数，当样本点落在超出允许的偏差范围ε 时，则计算损失。

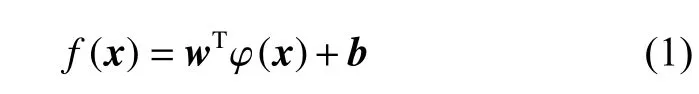
其中，w、b分别为超平面的法向量和截距。因为可能存在估计误差，不是所有的点都能落在 ε 间隔带内，因此引入松弛变量 (ξ,ξ∗) ，这样上述问题就转化为优化问题，此时目标函数和约束条件可以表示为

式中：C为惩罚系数，它可以调节权重以平衡线性拟合的精准度； ε 为不敏感参数。引入拉格朗日乘子，利用对偶变换和非线性变换将目标函数转化为

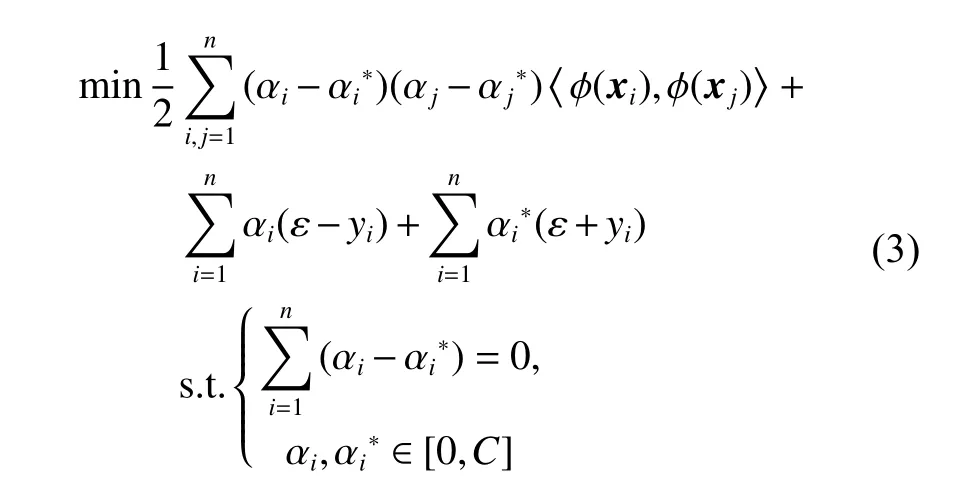
式中，k(xi,xj)=〈ϕ(xi),ϕ(xj)〉 为核函数。

核函数的选取会将样本映射到不同的特征空间，直接影响到预测模型的预测效果，本文选用偏差较小、学习性能较好的高斯核函数：

式中， σ 为核函数的宽度参数。

2 灰狼优化算法

灰狼优化算法是一种新的群智能优化算法，启发于灰狼种群的社会等级和狩猎行为。该算法模拟灰狼于自然界中分工、追捕和扑食猎物的行为，来获取待优化问题的最优解。狼群狩猎过程描述如下：

（1）社会等级分层。灰狼，擅奔跑，喜群居，群体内部遵守严格的社群等级制度。按照等级制度可将狼划分为4个等级，从高到低分别是α、β、δ和ω。计算每个灰狼个体的适应度，将适应度最好的3匹灰狼依次标记为α、β、δ，剩下的灰狼标记为ω。由α、β、δ发动追捕，ω执行猎物跟踪围剿，猎物的位置对应于优化问题的全局最优解。

（2）包围猎物。灰狼搜索猎物时会逐渐靠近再包围，首先灰狼个体会确定与猎物之间的距离

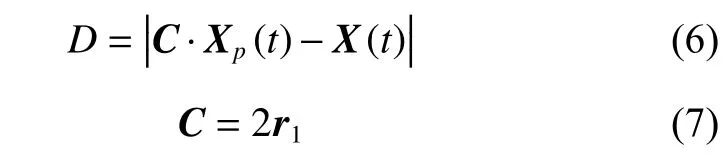
式中：t表示当前迭代次数；Xp(t) 表示猎物的位置向量；X(t) 表示灰狼的位置向量；C为系数向量；r1为取值在[0,1]之间的随机向量；D表示狼与猎物的距离。随后狼群要根据猎物方位对自己的位置进行更新：

式中：A为系数向量；r2为取值在[0,1]之间的随机向量；收敛因子a随着迭代次数由2线性递减至0。

（3）狩猎。当灰狼判断出猎物所在的位置时，追捕行动将由头狼α带领β狼和δ狼发动。在狼群中，α、β、δ能力最强，最靠近猎物，利用三者的位置关系来判断猎物所在方位，引导狼群向猎物位置进击，经过多次的定位和挪动，最终捕获猎物。位置更新的过程如下：

其中：X(t+1) 为更新后的灰狼个体位置。ω狼在3匹头狼的引导下向猎物位置方向移动。

3 改进灰狼算法

3.1 基于混沌Tent映射的初始化策略

传统GWO算法解决优化问题时往往基于随机性产生初始种群，这使得初始种群分布不均，导致寻优速度降低。而混沌运动具备随机性、规律性和遍历性的特性，利用这些优点可以产生较好的多样性初始种群，改善全局搜索能力。现有的混沌映射有Tent 映射、Logistic映射等，不同的混沌映射对函数优化性能有不同的影响。Logistic映射是目前使用较多的混沌映射，但该映射在[0, 0.1]和[0.9, 1]两个区间内的高分布概率会影响优化算法的收敛速度。文献[28]指出Tent映射遍历均匀性强于Logistic 映射，使得初始值较均匀地分布于[0, 1]之间，并经过严谨的数学推理，证明了Tent映射可以作为产生优化算法的混沌序列。

Tent 映射表达式如下：

式中：xt为第t序列值；u为混沌参数。当u=0.5时，所产生的序列均匀分布，其对不同的参数的变化不敏感，有着近似一致的分布密度，这种最典型的Tent映射表示如下：

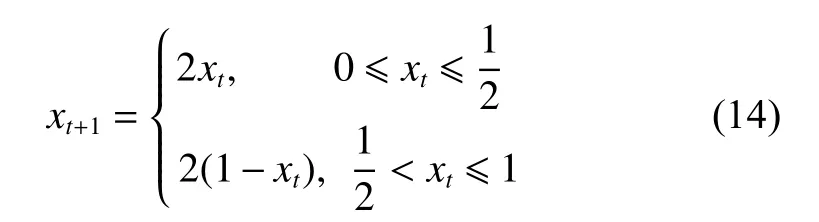
基于Tent映射的特性，为避免迭代落入小周期循环，在可行域中产生Tent混沌序列的具体步骤描述如下：

（1） 随机产生初值x0在[0, 1]之间(避免x0落入小周期(0, 2, 0, 4, 0.6, 0.8))，记入标志组z，z(1)=x0,i=j=1；

（2） 按式(14)进行迭代，迭代i自增1，产生一个x序列；

（3） 若达到最大迭代次数，则跳转到步骤（5）；否则，若xi={0,0.25,0.5,0.75} 或xi=xi−k，k={0,1,2,3,4} ，（即x落入不动点或周期小循环），则转向步骤（4），否则回到步骤（2）；

（4） 按x(i)=z(j+1)=z(j)+ε 改变迭代值，其中ε 为随机数，j=j+1 ，返回步骤（2）；

（5） 运行终止，保存x序列。

3.2 控制参数自适应调整策略

GWO算法的实现主要在于猎物定位和狼群移动，灰狼个体的位置更新受参数A影响。当 |A|>1时，狼群扩大搜索范围，进行全局搜索，以找到更优候选解；当 |A|＜1 时，狼群缩小搜索范围，于局部区域进行精细搜索。A值又随收敛因子a而变化，即控制参数a能协调GWO算法的全局和局部搜索能力。文献[29]提出了非线性变化收敛因子，并通过测试函数优化证实控制参数非线性变化策略比线性策略搜索效果更佳。本文引入了一种随迭代次数增加而非线性变化的收敛因子a，公式如下：

式中：T为当前迭代次数；Tmax为最大迭代次数。

该非线性（Improved）收敛因子与标准（Original）灰狼算法中的线性收敛因子的动态变化曲线如图1所示。

图1 收敛因子变化曲线Fig. 1 Change curves of convergence factors

由图1可以看出，含非线性变化的收敛因子a在算法进化初期递减速度慢，探索更优解，避免陷入局部最优，从而增强算法的全局勘探能力；在算法进化后期, 递减速度快，加快寻优速度，从而改善算法的局部搜索能力。

3.3 灰狼算法中的差分进化

差分进化算法作为一种模拟生物进化机制的全局搜索算法，通过变异、交叉和选择使种群不断地从低级向高级进化，受此思想影响，将差分进化思想融入GWO算法中，以弥补 GWO 算法易陷入局部极值的不足。

为保证种群竞争力，本文选取灰狼β和δ个体作为进化种群的父代，求其差分矢量，进行动态缩放因子后再与灰狼α进行合成，构建基于差分进化策略的GWO算法的变异因子。该变异因子的函数表达式为

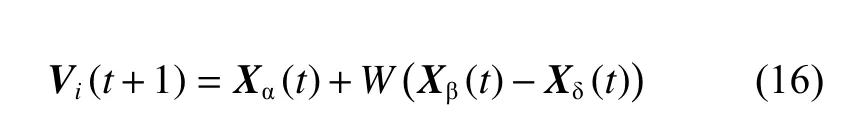
式中：W为动态变化的缩放因子，其取值范围为[0,2]。

式中：CR表示交叉概率常数；rand(j)表示在[0,1]内服从均匀分布的随机数；rand(i)表示随机的维度，可以保证狼群个体矢量最少一维变量来自变异矢量。

狼群中的个体之间通过竞争会产生新一代个体，经过变异与交叉操作而产生的中间个体与原个体进行竞争，选择适应度好的个体作为下一代。

3.4 IGWO算法测试仿真

为了验证改进灰狼算法的性能，本文选取4个Benchmark基准函数对算法进行寻优测试，充分考察算法的收敛速度和寻优精度。基准测试函数如表1所示，其中Sphere和Rosenbrock为单峰测试函数，Ackley和Rastrigin为多峰测试函数。

表1 基准测试函数Table 1 Benchmark test functions

各算法参数设置如下：PSO算法粒子数n= 30，学习因子c1=1.5，c2=1.5，惯性权重w= 0.8；ABC算法蜂群总数n= 30, 跟随蜂和引领蜂数目分别为15；GWO和IGWO算法狼群规模均取30，交叉概率因子CR取0.4。算法在python3.7环境下运行，测试函数维数均取30，最大迭代次数为500。对每个测试函数独立运行30次，其优化结果如表2所示，其中Best、Ave、Worst分别为运行30次的适应度函数值的最优值、平均值、最差值，Sd为标准差。

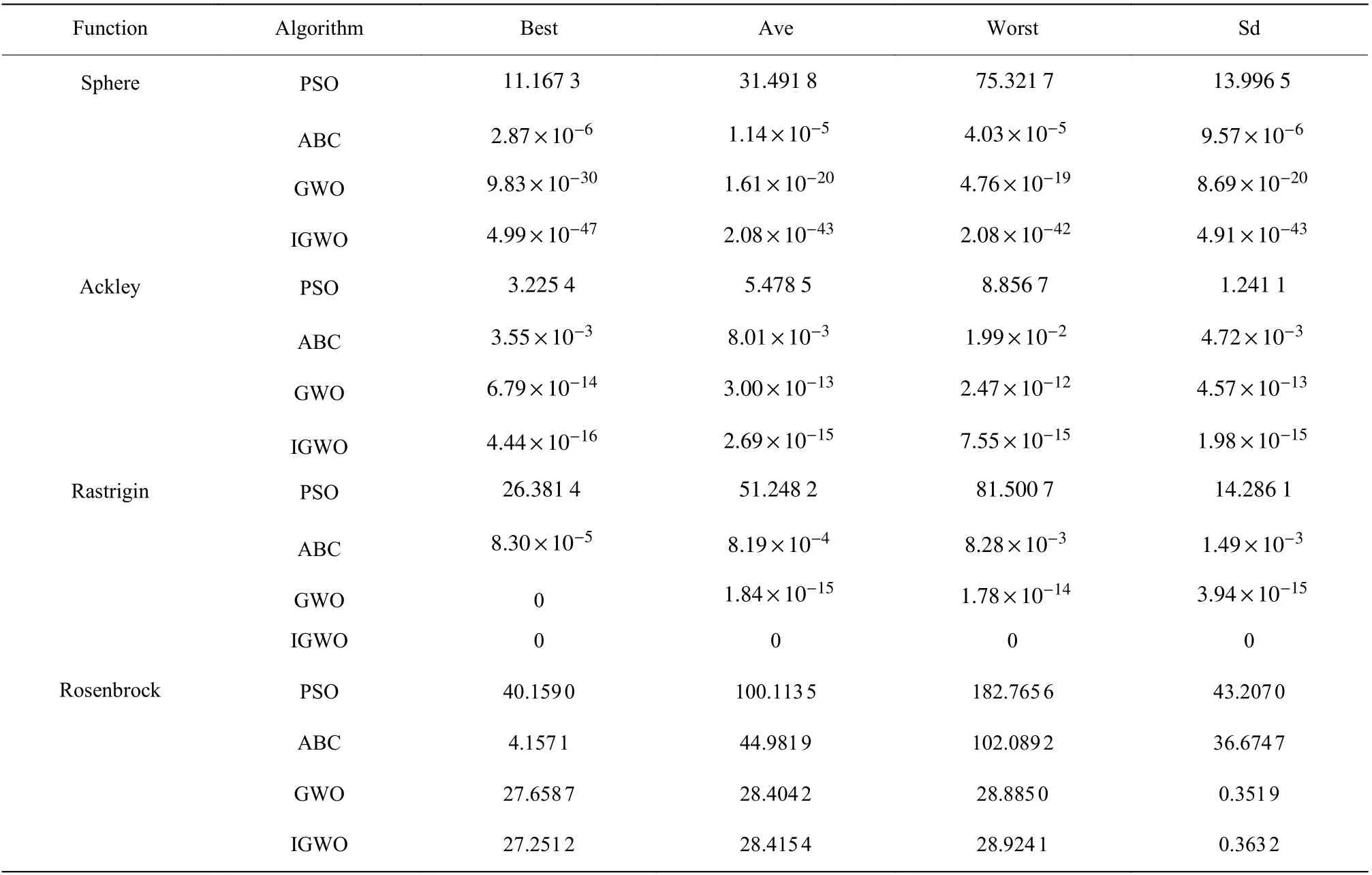
表2 基准测试函数优化结果对比Table 2 Comparison of optimization results of benchmark test functions

由表2可知，对于Ackley函数，IGWO算法能跳出局部最优，使寻优值无限趋向于0；特别是对于多峰二次函数Rastrigin, IGWO 算法达到了理论最优值，说明IGWO算法提高了测试函数的寻优精度且具有克服局部最优的能力。对于Sphere、Ackley、Rastrigin函数，IGWO算法相比PSO、ABC、GWO算法得到的平均值和标准差都最为理想，这表明IGWO算法具备较好的稳定性和鲁棒性。

图2所示为搜索过程中各种算法在测试函数上的收敛曲线。可以看出在相同的迭代次数下，IGWO和GWO算法相比于PSO和ABC算法，收敛速度快且搜索精度高。在搜索初期，IGWO和GWO算法的进化速度相当，但随着迭代次数的增加，GWO算法达到寻优停滞状态，而IGWO算法在多峰函数上的寻优效果更为理想。综上分析，IGWO算法具有较强的全局勘探能力和局部开发能力，在收敛速度和优化精度上均有明显的提高，同时还保持着较好的有效性和鲁棒性。

图2 PSO、ABC、GWO和IGWO在测试函数上的收敛曲线Fig. 2 Convergence curves of PSO, ABC, GWO and IGWO on the test functions

4 基于IGWO–SVR的锌耗预测建模及仿真实验验证

4.1 IGWO优化SVR

支持向量机回归的参数选取对模型的预测精度有着关键性的影响，其中有两个重要参数：惩罚系数C和径向基核函数参数 γ ，目前参数取值多是通过经验、试凑或是网格搜索。本文采用IGWO算法对SVR的C和 γ 进行寻优（IGWO-SVR），并以优化后的参数建立回归预测模型。IGWO-SVR算法流程图如图3所示。建模的具体实施步骤如下：

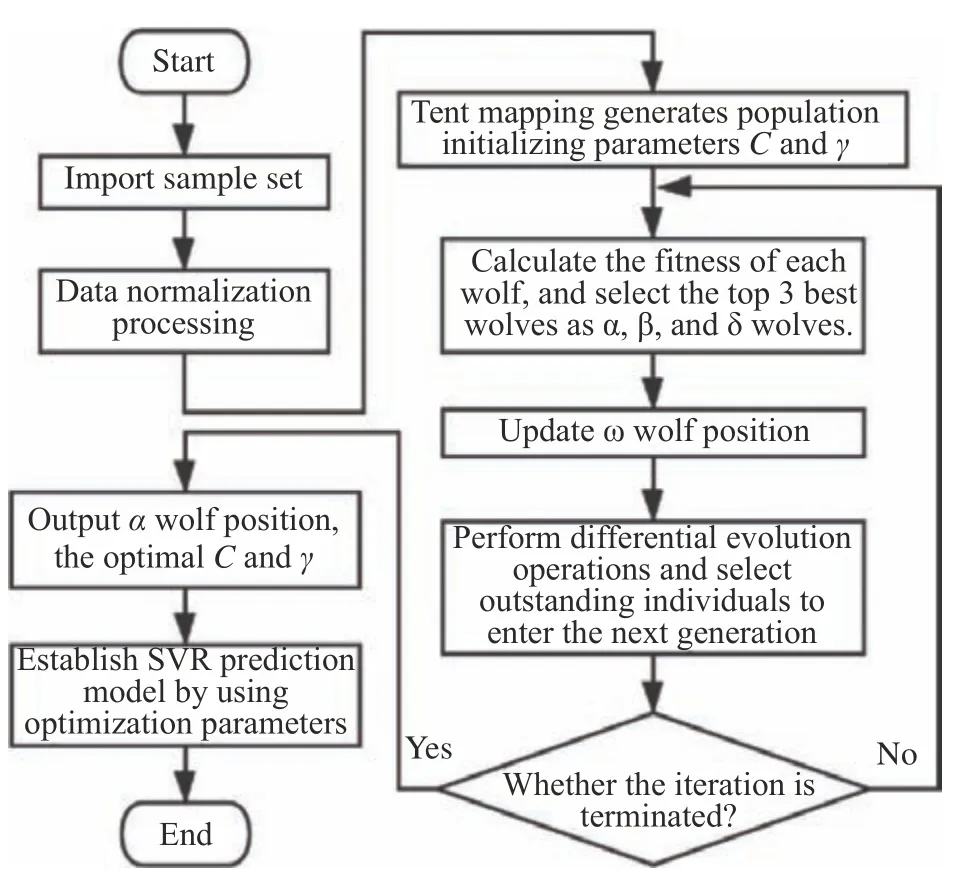
图3 IGWO-SVR算法流程图Fig. 3 Flow chart of IGWO-SVR algorithm

（1）数据预处理。对样本数据进行归一化，使得原始样本特征映射到[0,1]区间。

（2）参数寻优:

（a）设定相关参数，设置种群规模N、最大迭代次数T以及C和 γ 寻优范围。

（b）初始化狼群，根据式(14)Tent混沌序列的具体生成步骤，利用Tent映射产生灰狼个体 {Xi,i=1,2,···,N}，每只灰狼Xi对应的位置向量Pi由C和γ组成。

（c）计算适应度，根据位置向量Pi所包含的参数在训练集下进行SVR模型训练，以均方误差为适应度函数，计算灰狼个体的适应度值 {fi,i=1,2,···,N} ，按照适应度值大小对狼群分级，选出适应度最好的灰狼标记为α、β、δ。

（d）更新灰狼位置，根据式(10)、(11)和(12)对剩余的ω狼进行位置更新。

（e）差分进化操作，根据式(16)由狼群父代个体求差分变量，构建变异因子，再根据式(17)经交叉和选择后，择更优灰狼个体进入下一代种群。

（f）判断迭代次数是否超过最大迭代次数，若是，搜索过程结束，输出α狼的位置，即最优参数C和 γ ；若否，则返回步骤（c）继续参数优化。

（3）模型预测。提取最优参数构建SVR预测模型进行训练，并利用该模型对测试样本进行预测，经反归一化后输出结果。

4.2 基于IGWO- SVR的锌耗预测仿真

实验样本来自某钢厂的部分历史生产数据，经过数据预处理后，最终保留808个数据样本，随机选取80%作为训练样本，剩余20%作为测试样本。以分镀层类型的合同重量和目标锌耗等4个特征量作为输入，实际锌锭总耗量作为输出，建立IGWOSVR锌耗预测模型。为验证建模方法的有效性和优越性，分别采用PSO、GWO和IGWO对SVR进行参数优化。在仿真实验中，优化算法的种群规模均设为20，最大迭代次数均设为50，C和γ的上下限设置为0.01～100。各算法在训练集下进行SVR模型训练，以均方误差为适应度函数，进行交叉验证来优化参数，得到的最优参数如表3所示，适应度下降曲线如图4所示。

表3 各算法的参数寻优结果Table 3 Parameters optimization results of each algorithms

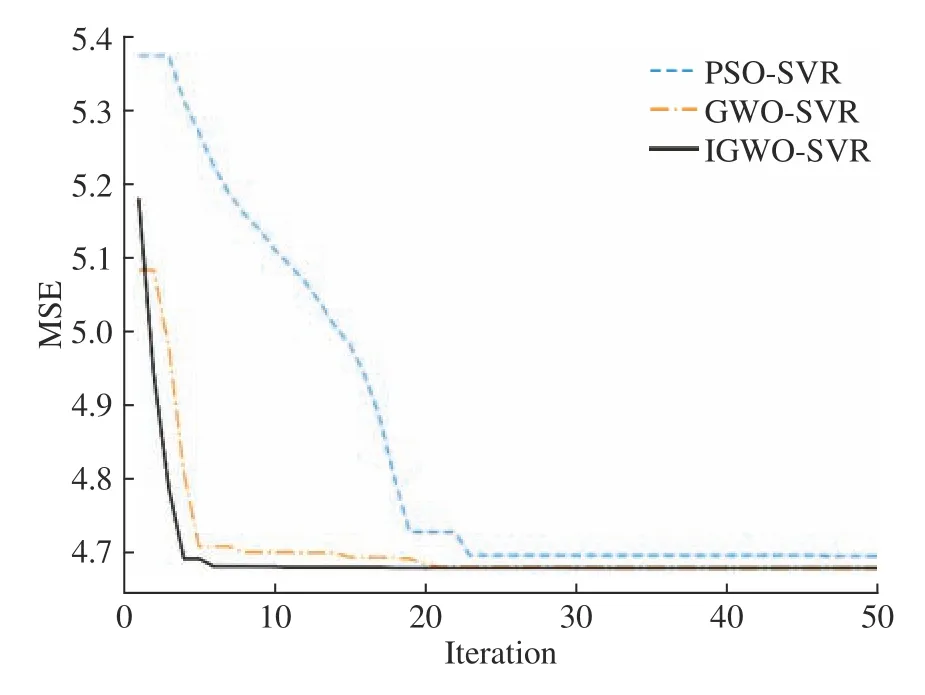
图4 IGWO-SVR、PSO-SVR、GWO-SVR参数优化过程的适应度下降曲线Fig. 4 Fitness decline curves of IGWO-SVR, PSO-SVR, GWOSVR parameter optimization process

采用寻优后参数分别构建PSO-SVR、GWOSVR及IGWO-SVR的锌耗预测模型，并利用训练完的模型进行预测。为了评价模型预测效果，选用均方误差（MSE）、平均绝对百分误差(MAPE)和决定性系数（R2）作为评价指标，公式如下：

其中：yi、、分别表示数据原始值、预测数据均值和原始数据均值。表4中示出了SVR、PSO-SVR、GWO-SVR、IGWO-SVR模型的性能对比结果。

表4 SVR、PSO-SVR、GWO-SVR、IGWO-SVR模型性能对比结果Table 4 Performance comparison results of SVR, PSO-SVR,GWO-SVR and IGWO-SVR models

图5示出了IGWO-SVR模型锌耗预测值与实际值的对比结果。由图5和表4可以看出，IGWOSVR锌耗模型预测曲线与实际曲线的贴合程度较高，模型的R2达到了0.8743，均高于另外3种预测模型，且其均方差和平均绝对百分误差也均为最小，进一步说明IGWO-SVR模型具有更高的预测精度。

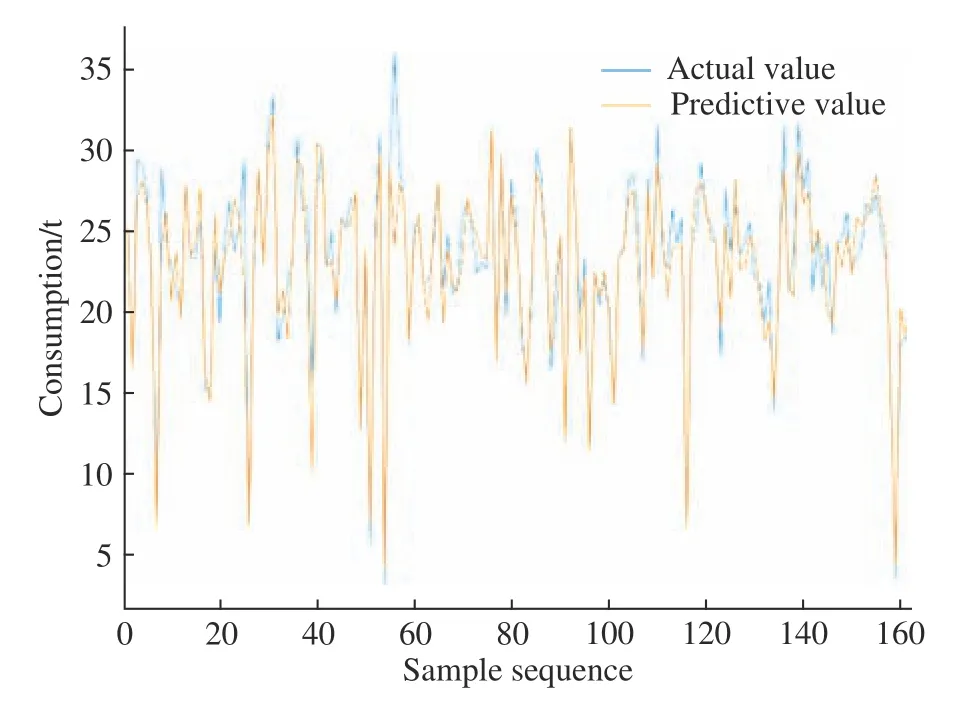
图5 IGWO-SVR锌耗模型预测结果Fig. 5 Prediction results of IGWO-SVR zinc consumption model

5 结束语

本文提出了一种基于改进灰狼算法优化的支持向量回归的建模预测方法，引入混沌Tent映射以增强初始种群的多样性和分布均匀性，采用非线性收敛因子并融合差分进化算法以平衡算法的全局和局部搜索能力。为验证改进灰狼优化算法的有效性，采用典型基准测试函数进行仿真实验，实验结果表明，其综合性能优越，寻优精度高，且具有较好的稳定性和鲁棒性。采用改进的灰狼算法对SVR进行参数优化，并根据最优参数构建锌耗预测模型，有效提高了锌耗预测精度，为解决高维、非线性的工业问题提供了新的解决途径。下一步工作考虑将IGWO算法应用于求解更复杂的组合优化问题，并结合其他智能优化算法，提出性能更好的全局优化算法。