基于长期实测数据的西北地区风力发电场风速风向联合概率分布分析
李万润,张广隶,李 林,杜永峰,3
(1.兰州理工大学 防震减灾研究所,甘肃 兰州 730050;2.兰州理工大学 土木工程学院,甘肃 兰州 730050;3.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050;4.兰州市气象局,甘肃 兰州 730020)
近年来,风电行业高速发展,2018年全球新增风电装机容量为51.3 GW.截止到2018年年底,全球累积装机容量已达591 GW.风力发电机属于风敏感结构体系,风荷载在其结构设计和实际工作中均起控制作用.在相同风速不同风向下,风力发电机的结构响应不同[1],而目前针对风力发电机的结构响应分析中,所采用的基本风速大多不考虑风速风向联合分布.因此,构建合理的风速风向联合分布函数,考虑风速风向联合分布对结构响应的影响,根据一定重现期下推算得到的各风向对应基本风速进行风力机结构响应分析,可以进一步优化风力发电机的结构设计.
针对风速风向联合分布,国内外学者都开展了广泛的研究,Dargahi-Noubary[2]利用广义越界分布概型将极值分布概型归纳为三种极值分布:Gumble分布、Frechet分布和Weibull分布;Garcia等[3]利用西班牙纳瓦拉自治区气象站实测数据进行三种极值分布概型的拟合与检验,认为Weibull概型拟合结果最优;Simiu等[4]利用POT(peaks over threshold)方法估算飓风区极值风荷载,结果表明忽略风向影响的常规做法对于计算极值风荷载偏于保守;王钦华等[5]基于随机风振理论计算超高层建筑等效静力风荷载,研究结果表明,考虑风向对基本风压的影响,等效风荷载绝对值偏小;Johnson等[6]基于最大熵原理和边缘分布提出了一个变量为方向变量,一个变量为标量变量的联合分布模型,可应用于风速风向联合分布分析;陈隽等[7]利用谐波函数定义分布概型参数沿圆周的变化规律,提出了一种针对总体样本的风速风向联合概率分布分析方法;范文亮等[8]基于乘法定理拟合风向角混合分布及风速条件概率密度,构建了风速风向的二维连续联合分布模型;杨咏昕等[1]基于最小二乘法提出了一种风速风向联合分布的平均风统计方法,并解释了考虑风速风向联合分布的必要性;王浩等[9]针对苏通大桥7年的实测数据进行了风速风向联合分布分析,研究表明苏通大桥不考虑风向影响的抗风设计所采用的基本风速偏于保守.在风电领域,风力发电结构作为一种典型的风敏感结构,对风荷载引起的结构响应的研究一直是风力发电机结构设计中的首要问题.Yeter[10]对海上风力发电机的支撑结构在各种负载条件下的疲劳损伤进行了评估;陆越等[11]采用Davernport谱模拟风荷载进行风力发电机疲劳寿命研究;Ke等[12]利用谐波叠加法模拟风荷载,分析风力发电机在风荷载下的结构响应;余玮等[13]通过CFD(computational fluid dynamics)数值模拟获得风力发电机表面的风压分布系数,并利用由此得到的风荷载进行结构响应分析,得到了风力发电机在风荷载作用下的结构反应规律;李万润等[14]基于实测数据对西北地区风电场风塔的尾流特性进行分析,得出外围风塔实测风速更加接近高斯分布.可以看出,目前针对风力发电机风致振动响应的研究中,大多数为数值模拟计算,而在数值模拟风力机结构响应时,不论是将风荷载以节点力的形式作用于塔架进行结构响应计算,还是利用CFD进行流场分析,都很少考虑风向的影响.因此,为了更为准确科学地分析风力发电机结构的动力响应,有必要根据实测数据进行实际地区的风速风向联合分布分析.
本文基于甘肃气象局提供的甘肃六个风电场比较集中的地区(安西、玉门镇、酒泉、民勤、景泰、靖远)长达37年(1981年1月1日至2017年12月31日)的实测风速风向数据,依据阶段极值法抽取极值样本,通过引入风向频度函数得到不同风向上极值风速分布,利用最小二乘法拟合线性化后的风速风向联合分布概型的参数,进而预测10,50及100年重现期下各地区的基本风速,以期为西部地区风速风向联合分布的进一步分析提供基础,同时为西部地区风力发电机的设计、风致振动分析提供参考.
1 风速风向数据基本情况
截止到2018年年底,甘肃省风电总装机容量已达1 282万千瓦,位居全国各省区第四位.本文分析所涉及的甘肃六个地区(安西、玉门镇、酒泉、民勤、景泰、靖远)均为甘肃省风电场集中分布地区,各地区具体地理位置分布如图1所示.
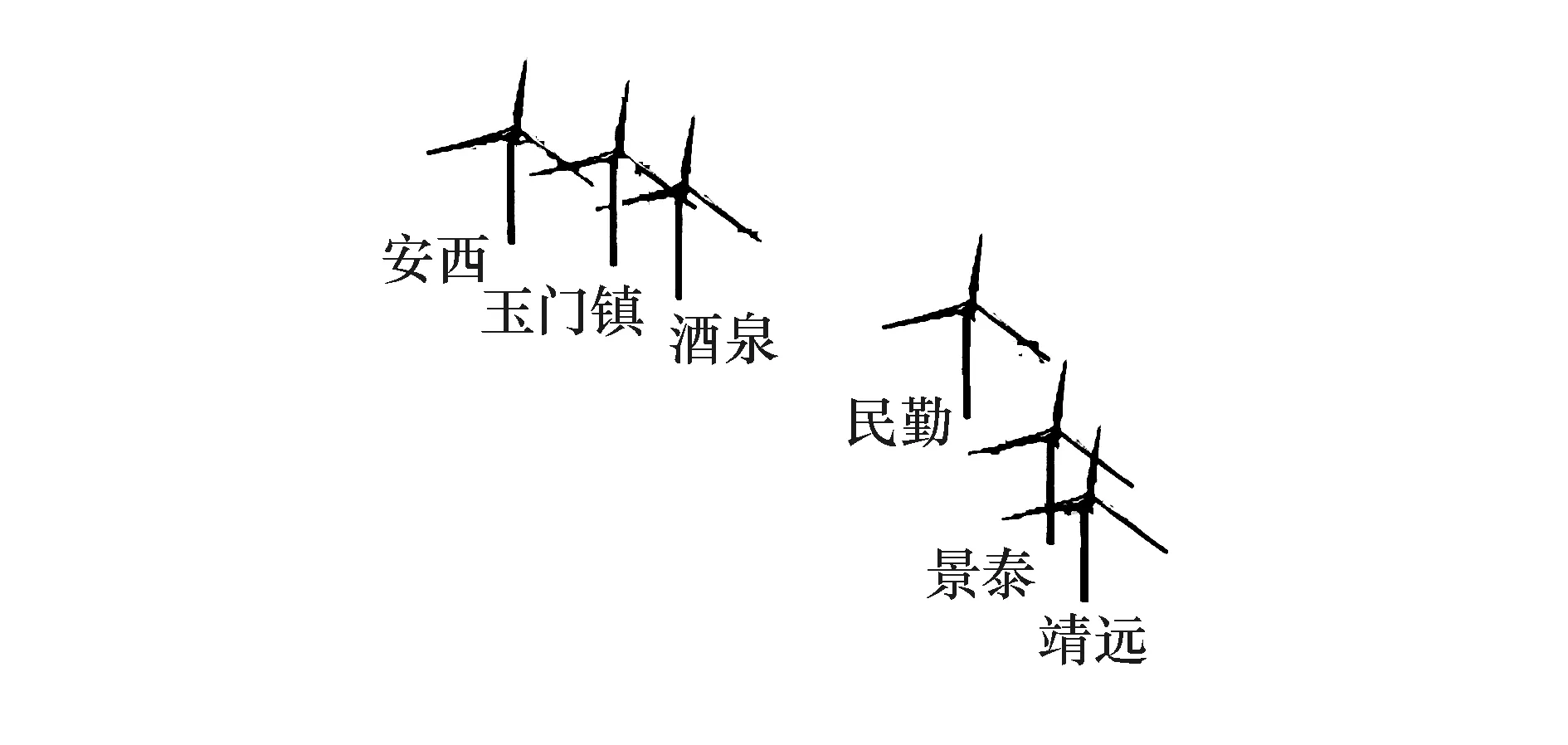
图1 甘肃六个地区地理位置分布Fig.1 Geographical distribution of six regions in Gansu
为了掌握地区气象资料,甘肃省气象局在这些地区都设有六要素自动气象站,对各地区的风向、风速、温度等6类气象要素进行观测,其采集系统精度高、准确性好,气象观测数据可用于风电环境考察.因此,本文主要选用这六个地区的六要素气象站所测得的各地区1981年1月1日至2017年12月31日的16个风向的风向记录及其对应的10 min平均时距的日最大风速值,并针对这些地区的实测风速风向数据进行分析,其结果可为后续的西部地区风力发电机风致响应分析提供支持.图2为由实测数据统计出的各地区1981年1月1日至2017年12月31日的日最大风速值.
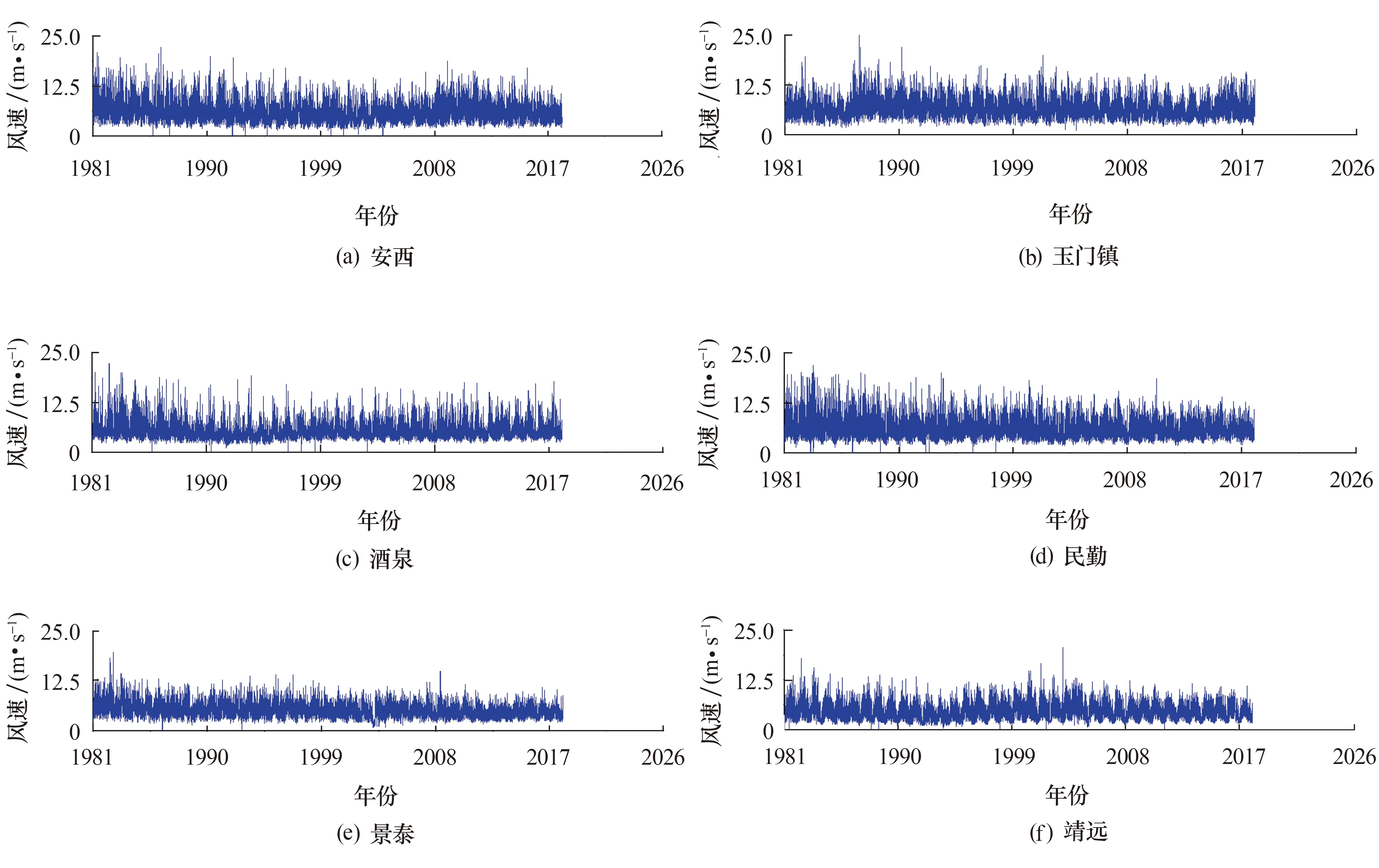
图2 各地区1981年-2017年日最大风速值Fig.2 Daily maximum wind speed from 1981-2017
2 极值风速样本的抽样分析
为预测风力发电机风致响应所需的基本风速,风速实测样本采用极值风速样本,因为极值风速样本的分布才是风速统计的关键.本文采用的抽样方法为阶段极值抽样方法,即将整体的风速数据样本以相同的时间间隔分为若干个子样,其中每个子样具有相同数量的风速风向数据,然后抽取每个子样中的极值风速及其对应的风向作为样本点进行统计.样本统计结果可以得到各地区的风向频度及各风向下的风速分布,并为后续的极值函数分布函数的检验和拟合提供数据.极值分布函数表达式为
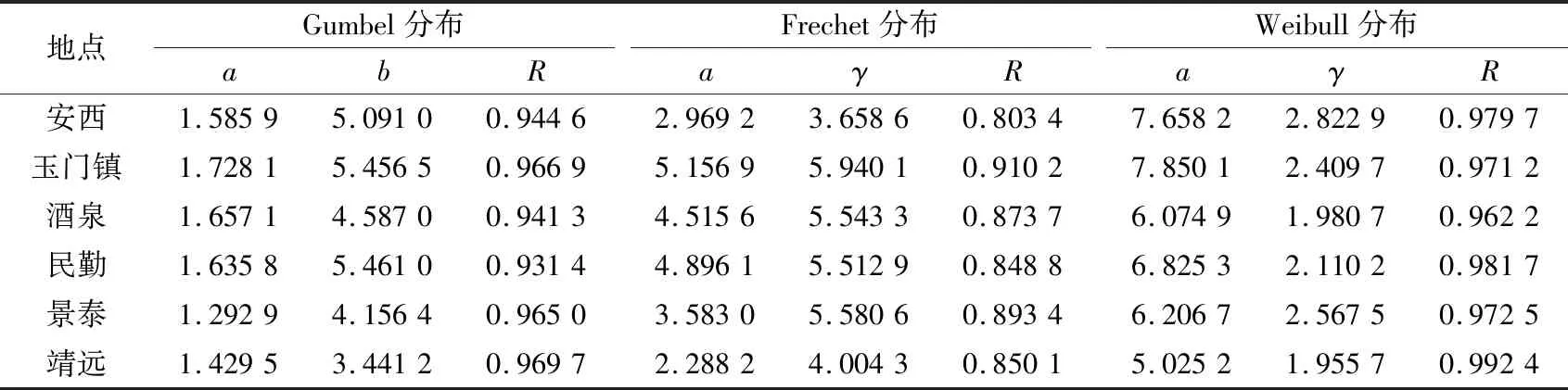
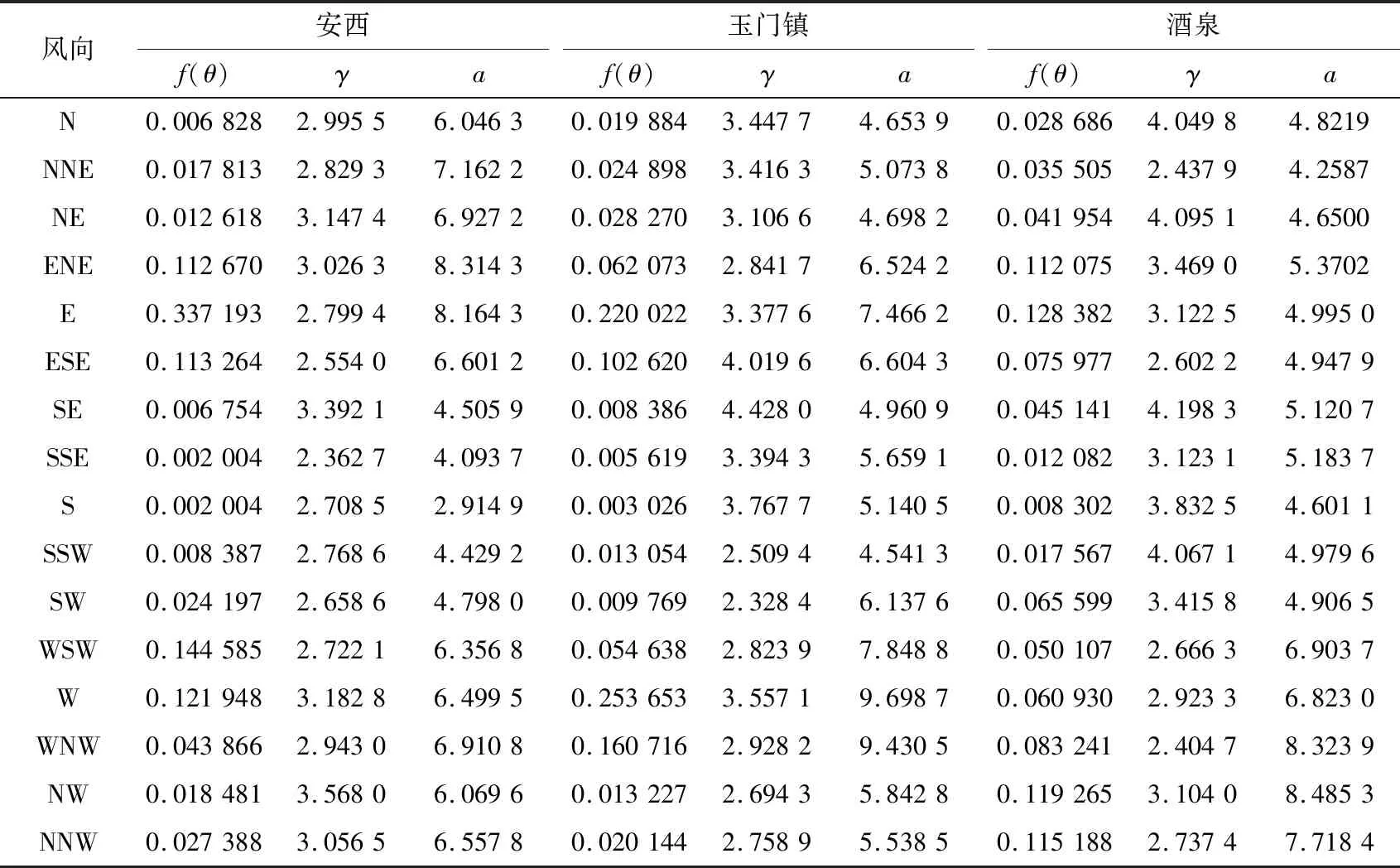
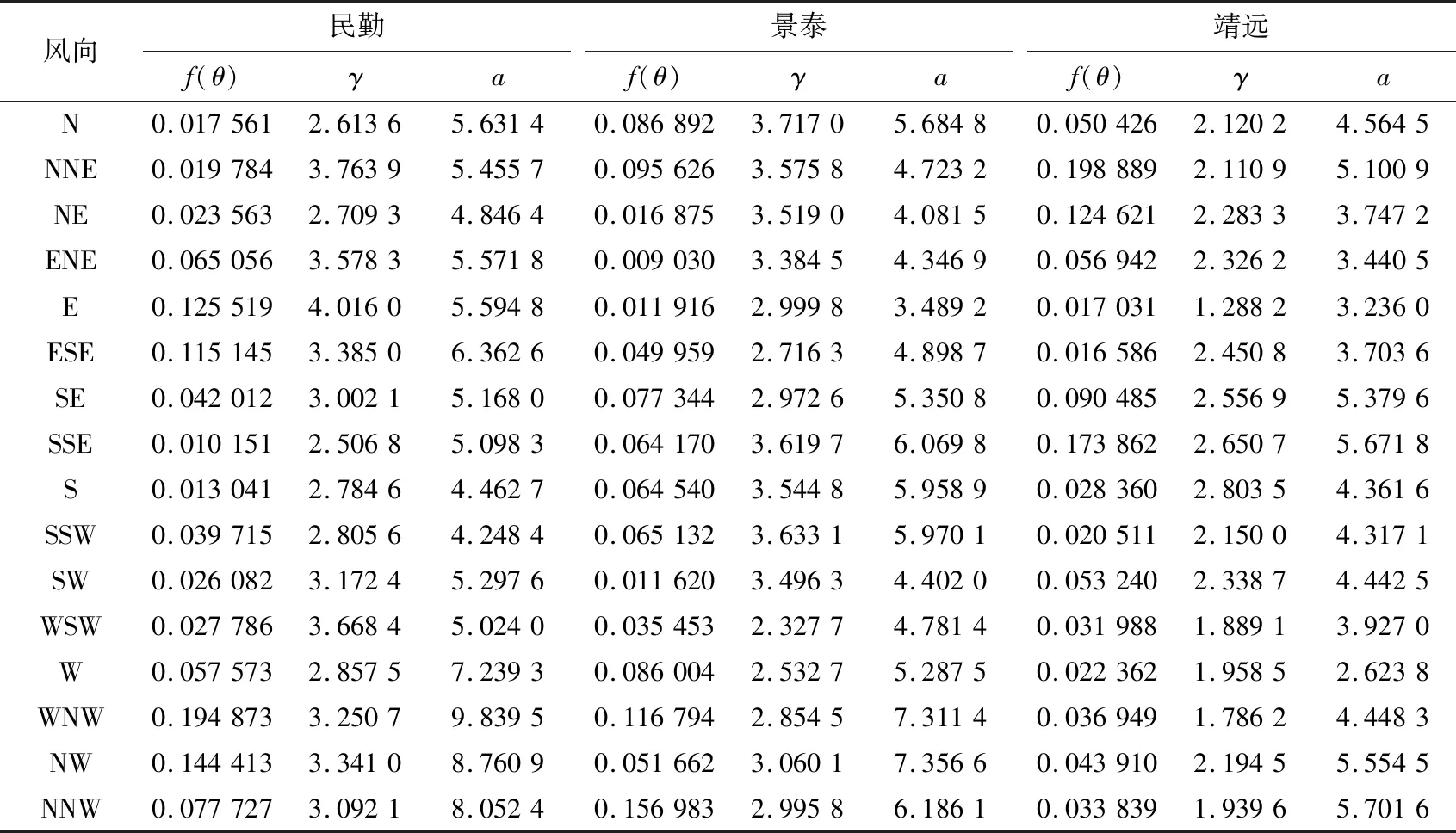
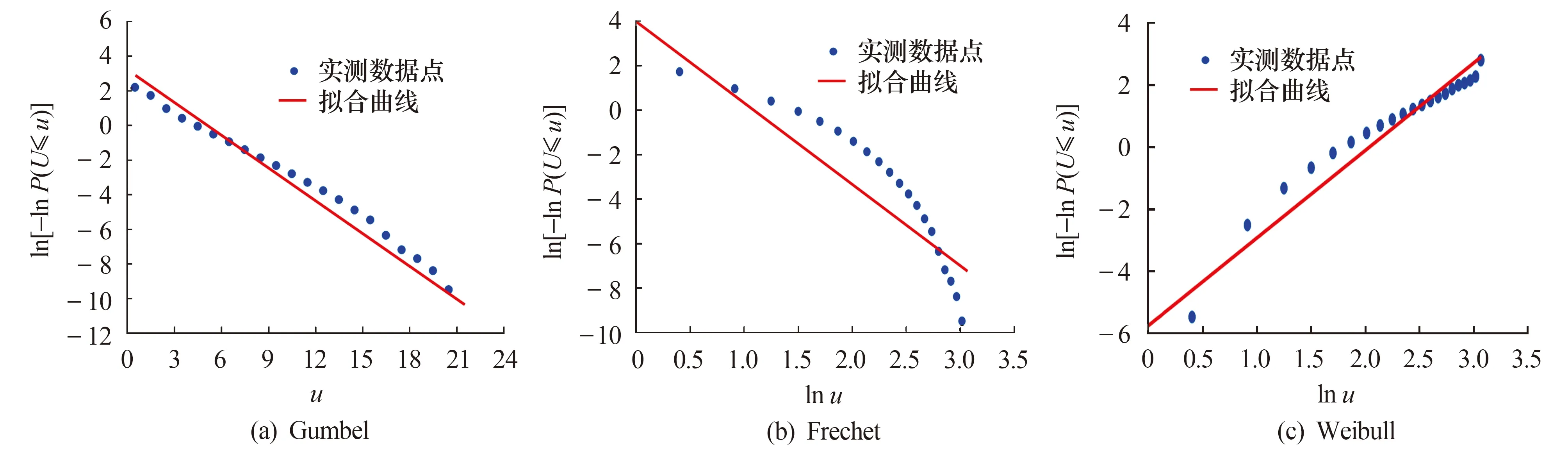
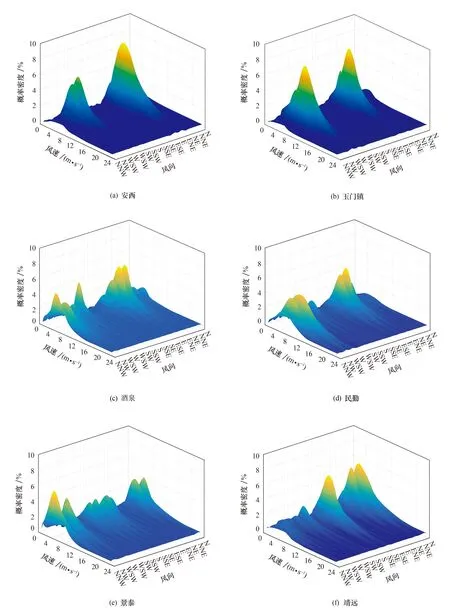
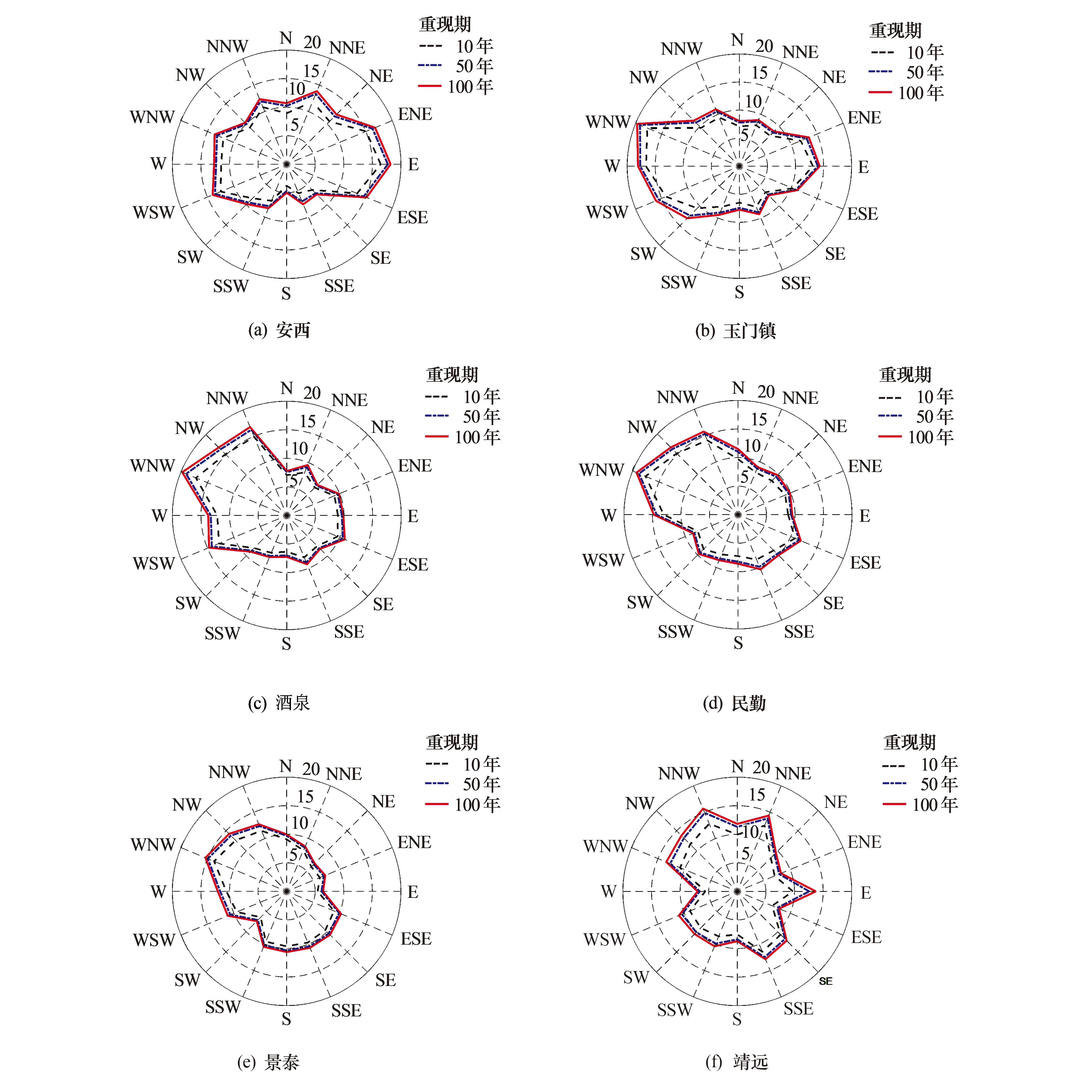
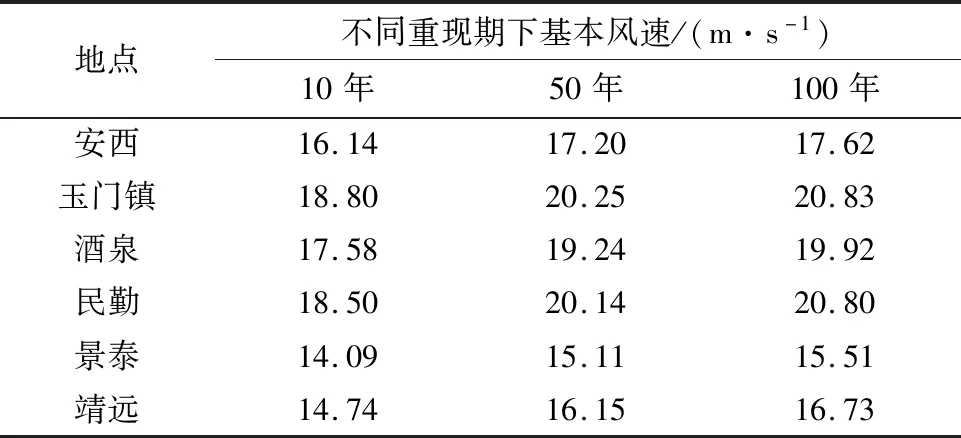
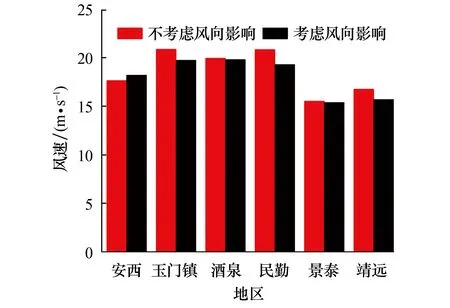
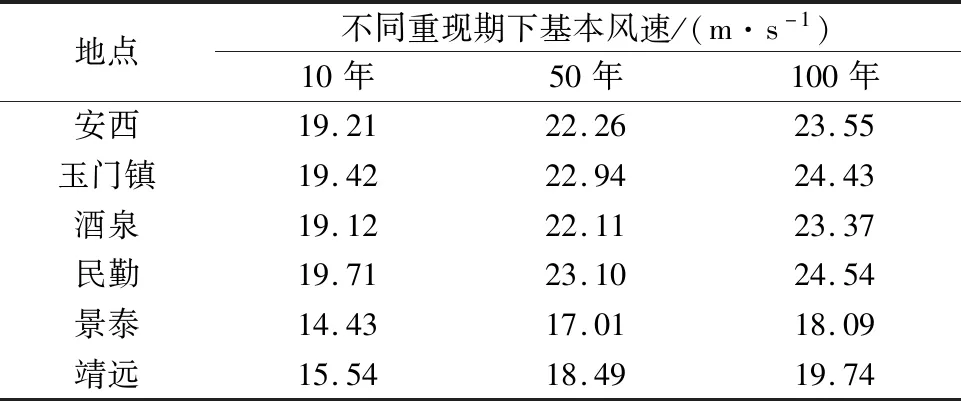
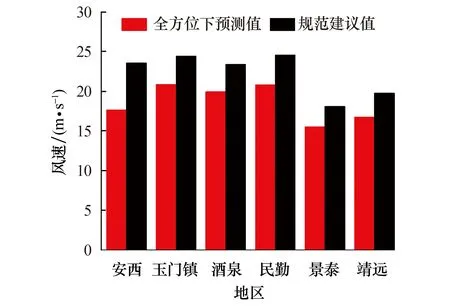
F(u,θ)=f(θ)Pu(U (1) 式中:f(θ)为风向频度函数;U为平均风速;θ为风向角;Pu(U 样本量的大小直接影响统计结果的准确性和基本风速预测的精度,因此为了保证样本数据的代表性,针对各地区1981年1月1日至2017年12月31日的风向记录及其对应的日最大风速值,以1 d长度为采样时间间隔进行阶段极值抽样,选取2 m/s为风速区间间隔,统计得到各地区的各风速区间在16个风向上的概率密度. 图3为各地区风速风向联合概率密度分布统计结果.后续的风速风向联合分布概型的拟合及各地区不同重现期下基本风速的预测均以此为基础. 图3 各地区风速风向概率密度柱状图Fig.3 Probability density histogram of wind speed and direction of each region 根据风速风向统计结果,在1981年1月1日至2017年12月31日期间,安西地区风向以E风向(33.719%)和WSW风向(14.459%)为主,最大风速为21.0 m/s(E风向);玉门镇地区风向以E风向(22.002%)和W风向(25.365%)为主,最大风速为25.0 m/s(WNW风向);酒泉地区风向以E风向(12.838%)和NW风向(11.926%)为主,最大风速为22.3 m/s(WNW风向);民勤地区风向以WNW风向(19.487%)和NW风向(14.441%)为主,最大风速为22.0 m/s(WNW风向);景泰地区风向以NNW风向(15.698%)和WNW风向(11.679%)为主,最大风速为19.7 m/s(WNW风向);靖远地区风向以NNE风向(19.889%)和SSE风向(17.386%)为主,最大风速为20.7 m/s(E风向).由此可以看出,各地区的风速分布在整个风向上基本呈双峰分布,因此在针对这些地区的风力发电机进行风致响应分析时,若不考虑风向的影响,其结构响应分析的结果精度势必会受到影响. 为了得到更加符合实际情况的基本风速,提高针对甘肃省风电场集中地区的风力发电机风致响应分析的结果精度,下面基于甘肃六个地区(安西、玉门镇、酒泉、民勤、景泰、靖远)的实测风速风向数据统计结果,进行三种联合分布概型的检验和拟合.在拟合风速风向联合分布函数时需遵循两个基本假定: 1) 不同风向的平均风速服从统一的极值分布概型. 2) 各地区不同风向的平均风速分布概型参数彼此独立,各风向参数值仅由该风向的极值风速数据拟合产生. 在风工程领域,极值分布概型分为三种极值分布:Gumble分布、Frechet分布和Weibull分布,三种概率分布函数如下所示. 1) Gumbel概率分布函数 (2) 2) Frechet概率分布函数 (3) 3) Weibull概率分布函数 PU(U>u|θ)=f(θ)exp[-(-u/a(θ))γ(θ)] (4) 式中:a、b和γ分别为比例、位置和形状参数. 在上述三种极值分布函数中的参数都是风向的函数,且各分布函数都有两个参数,因此可以将三种分布函数转化为线性函数后,利用最小二乘法拟合相关参数.最小二乘法的原理是通过最小化误差的平方和,寻找数据的最理想函数进行匹配,进而求解出拟合函数的待定参数.通过变换将三种分布函数化为线性函数,如下所示: 1) Gumbel概率分布函数 u=b-aln[-lnP(U≤u)] (5) 2) Frechet概率分布函数 ln[-lnP(U≤u)=-γ(lnu-lna) (6) 3) Weibull概率分布函数 ln [-lnP(U>u)]=γ(lnu-lna) (7) 本文利用甘肃气象站测得的1981—2017年各地区各风向上极值风速数据样本,拟合上述三种分布函数的参数,并以相关系数R为标准,衡量拟合结果的线性相关程度.图4为安西地区联合分布函数拟合结果图. 各地区三种概率分布函数拟合结果图趋势基本一致,这里不一一列举,现将甘肃六个地区联合分布参数拟合结果汇总为表1. 由图4和表1可以看出,各地区3种极值分布函数的拟合结果均具有较好的相关性,甘肃六个地区的Gumbel分布拟合结果相关系数R值在0.931 4至0.969 7之间,Frechet分布拟合结果相关系数R值在0.803 4至0.910 2之间,Weibull分布拟合结果相关系数R值在0.962 2至0.992 4之间,各地区的Weibull分布拟合系数R均更接近于1,因此Weibull概率分布更吻合实测数据.在接下来的研究中,针对甘肃各地区16个风向上的极值风速样本数据均采用Weibull风速风向联合分布函数进行参数分析.通过计算得到甘肃六个地区16个风向的参数拟合结果,拟合结果汇总为表2和表3. 表1 甘肃六地联合分布参数拟合结果Tab.1 Fitting results of joint distribution parameters of six region in Gansu 表2 甘肃安西、玉门镇、酒泉地区各风向分布参数拟合结果Tab.2 Fitting results of wind direction’s distribution parameters in Anxi,Yumenzhen and Jiuquan 表3 甘肃民勤、景泰、靖远地区各风向分布参数拟合结果Tab.3 Fitting results of wind direction's distribution parameters in Minqin,Jingtai and Jingyuan 图4 安西地区联合分布函数拟合结果图Fig.4 Fitting results of joint distribution function in Anxi 结合各地区各风向分布参数拟合结果与Weibull概率分布函数式(4)可得甘肃六个地区的风速风向联合概率分布模型如图5所示.对比图3中各地区的风速风向联合概率分布柱状图,两者较为接近,因此本文得到的甘肃六个地区的风速风向联合概率分布模型可以较好地拟合风速风向联合分布. 图5 各地区风速风向联合概率分布Fig.5 Joint probability distribution of wind speed and direction of each region K次强风样本极值风速与重现期为M下基本风速间的概率关系如下: pUm(Um (8) 式中:Um表示K次强风样本中的极值风速;UJ为给定重现期下的基本风速.简化式(8),可得K次强风样本极值风速大于基本风速的概率PUm(Um>UJ∣θ)为: PUm(Um>UJ|θ)=1/M= K[PU(U>UJ|θ)] (9) 本文采用1 d长度为阶段极值采样的时间间隔进行抽样,K取值为365.联合式(9)与式(4)可得,给定重现期下Weibull极值分布的基本风速满足如下函数: (10) 根据各地区极值风速样本的参数及风向频度函数f(θ)拟合结果,由式(10)可得各地区各风向基于Weibull极值概型的重现期为10,50及100年的基本风速.各地区不同重现期下基本风速玫瑰图如图6所示. 图6 各地区基于Weibull极值概型的基本风速玫瑰图Fig.6 Rose chart of basic wind speed based on Weibull distribution in each region 为比较考虑风速风向概率与不考虑风速风向概率的基本风速的差别,结合表1中各地区全方位下的参数拟合结果,得到各地区全方位下的基本风速预测结果如表4所示.图7为100年重现期各地区不考虑风向影响即全方位下的基本风速与考虑风向影响的各地区基本风速对比图. 表4 各地区全方位下基本风速预测结果Tab.4 Forecast results of basic wind speed in all directions in each region 图7 各地区风向对基本风速影响对比图Fig.7 Comparison of the influence of wind direction on basic wind speed in each region 由表4、图6及图7可得,甘肃六个地区中,安西地区100年重现期的最大基本风速为E风向的18.19 m/s,玉门镇地区100年重现期的最大基本风速为WNW风向的19.72 m/s,酒泉地区100年重现期的最大基本风速为WNW风向的19.78 m/s,民勤地区100年重现期的最大基本风速为WNW风向的19.26 m/s,景泰地区100年重现期的最大基本风速为WNW风向的15.38 m/s,靖远地区100年重现期的最大基本风速为NNW风向的15.68 m/s.除甘肃安西地区E风向外,甘肃六个地区各个风向上不同重现期的基本风速预测结果均小于各地区全方位下基本风速预测结果.安西地区E风向在100年重现期的基本风速为18.19 m/s,而在全方位下的基本风速为17.62 m/s.因此在大多数情况下,不考虑风向影响,根据全方位下的基本风速进行设计是安全的,但在个别地区的主风向的基本风速有超过全方位下基本风速的可能.这也说明了在结构设计时考虑风向的影响是具有实际意义的,针对特定地区进行风速风向联合分布分析能更好的为设计提供参考. 我国的《建筑结构荷载规范》GB50009-2012[15]在风速的统计计算中采用Gumbel极值风速分布概型,对于重现期为R的最大风速XR,规范给出的计算公式如下所示. XR=u-ln[ln(R/(R-1))]/α (11) 式中:u为分布的位置参数,α为分布的尺度参数.参数值可由标准差σ和平均值μ求得,如下: 规范GB50009-2012中要求风速的统计样本应采用年最大值,且不考虑风向的影响.依据本文所采用的实测数据统计结果和式(11~13),可得到各地区最大基本风速规范建议值如表5所示. 表5 各地区最大基本风速规范建议值Tab.5 Recommended values of maximum basic wind speed in each region 对比表4和表5中数据及图8可得,本文所采用Weibull风速风向联合分布函数参数进行预测得到的各地区全方位下基本风速,与规范GB50009-2012采用极值Ⅰ型的概率分布计算得到的各地区最大基本风速结果较为接近,说明本文所采用的分析方法具有足够的计算精度,另外值得注意的是,各地区最大基本风速规范建议值均大于基于Weibull极值概型拟合得到的各地区全方位下基本风速,说明目前规范所采用的各地区最大基本风速值是偏于保守的. 图8 各地区风速预测值与规范建议值对比图Fig.8 Comparison of wind speed prediction value and standard recommended value in each region 针对甘肃气象局提供的甘肃六个地区(安西、玉门镇、酒泉、民勤、景泰、靖远)长达37年(1981年1月1日至2017年12月31日)的实测风速风向数据,本文采用阶段极值法抽取极值样本,分析各地区风速风向分布,并将Gumbel,Frechet和Weibull分布函数线性化,利用最小二乘法拟合各地区全方位及不同风速风向分布参数,进而预测10,50及100年重现期下各地区的基本风速,为西部地区风力发电机风致响应分析提供依据,通过研究得到以下结论: 1) 甘肃六个地区(安西、玉门镇、酒泉、民勤、景泰、靖远)的风速分布在整个风向上基本呈双峰分布,在针对这些地区的风力发电机进行风致响应分析时,仅考虑单风向的影响不符合实际情况. 2) Gumbel,Frechet和Weibull分布函数分布函数与样本数据均具有较好的相关性,甘肃六个地区的三种分布拟合结果中,Weibull分布拟合系数R更接近于1,因此Weibull概率分布更吻合实测数据. 3) 除了安西地区E风向在100年重现期的基本风速大于全方位下基本风速,甘肃六个地区各个风向上不同重现期的基本风速估计结果均小于各地区全方位下基本风速估计结果.因此在大多数情况下,不考虑风向影响而根据全方位下的基本风速进行设计是安全的,但在个别地区的主风向的基本风速有超过全方位下基本风速的可能.在实际分析设计时,有必要考虑风速风向联合分布的影响. 4) 各地区10,50及100年重现期下的基本风速预测值均小于规范计算值,说明目前规范所采用的各地区最大基本风速值是偏于保守的.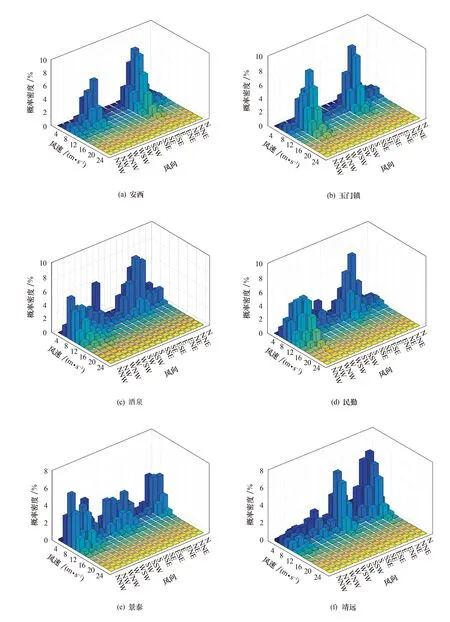
3 联合分布概型的检验和拟合
4 联合分布的基本风速的确定
5 与规范建议值对比分析
6 结论

