一种基于加权深度森林的离群数据挖掘算法

李瑞峰，杨海峰，蔡江辉，荀亚玲，周永祥

(太原科技大学 计算机科学与技术学院，太原 030024)

1 引 言

离群点是在同一数据集中，与其他数据有明显差异、偏离大多数数据的异常点.离群点检测被广泛应用于计算机网络的非法访问、极端天气的发现、手机网络诈骗等领域[1].能够在大数据中准确高效地找到离群点，是机器学习的主要任务之一.

目前，机器学习中离群点的检测方法主要包括基于距离、密度、统计以及聚类等方法.基于距离的方法通过计算点之间的距离，将与邻域内其他点距离较远的点视为离群点[2]，Liu等[3]对不同类型的对象进行组合，通过计算对象间的相似度及其语义信息来识别离群点.在基于聚类的方法中，将不属于任何一个簇的样本点定义为离群点，Huang等[4]使用RA-clust算法和综合假设检验相结合的方法对离群点进行高效检测.基于密度的方法使用离群因子表示数据的离群程度，离群因子数值越大，离群的程度越大[5].Su等[6]利用重新定义的局部偏差系数与多级查询相结合的方法对局部离群点进行检测.Shao等[7]使用共享的最近邻居密度来识别离群点.Hoang等[8]通过对LOF算法进行改进，对数据的近邻和逆近邻点计算离群因子，使其能够解决由不同密度引起的边缘误判问题，提高离群点检测的准确性.基于统计的方法先使用正常数据建立一个线性模型，将该模型低概率区域中的点视为离群点.例如，PCA算法[9]，一类支持向量机算法(OCSVM)[10].但这些算法大多都较难应对复杂数据的′维数灾难′问题，在高维属性中存在较多的无关属性时，在一定程度上异常点容易被无关属性掩盖，影响异常点的检测效率.

深度森林是一种有效的机器学习方法，该算法不涉及大规模的距离计算，也不取决于其近邻密度的大小，与传统的离群点挖掘算法相比具有更适用于海量高维数据、较少的超参数优化的特点.与上述方法不同，深度森林算法主要是通过集成思想来对数据特征进行划分并计算其概率分布.但是森林级联模块中的深度森林算法的森林特征随机选择性大，可能会导致很多无关属性被作为根节点，从而影响算法的性能与效率.针对上述缺点，本文对深度森林算法进行了改进，提出了一种基于加权深度森林的离群数据挖掘算法WDF(Weight Deep Forest).算法的主要思想为：首先使用滑动窗口方法对数据进行粒度扫描；然后，在级联森林模块构建过程中，将粒度扫描模块中得到的概率向量进行层级训练，根据每个实例的概率分数来计算森林的预测准确率，并定义了权重因子μ，使用权重因子μ赋予每个森林相应的权重，μ越高，对应的权重值越大，有效地减少森林中特征随机选择对算法性能的影响；其次，由于样本数据中离群数据分布的不同，重新定义了局部孤立因子α以及阈值函数F(r)，根据数据的类密度对孤立因子α进行计算，α值越大，数据离群的可能性也就越大，α大于阈值函数F(r)的数据为离群数据，从而提高离群点检测的正确性；最后采用UCI数据集和恒星光谱数据验证了该算法的有效性.

2 理论基础

在深度森林算法[11]中，主要包括两部分，多粒度扫描模块和级联森林结构模块，其模型结构如图1和图2所示.

图1 多粒度扫描模块框架Fig.1 Multi-granularity scanning module framework

图2 级联森林结构模块框架Fig.2 Cascading forest structure module framework

如图1所示，在多粒度扫描模块中，通过不同大小的窗口m1和m2将n维数据划分为(n-m1+1)个m1维，(n-m2+1)个m2维的数据实例，通过对两个森林进行训练，生成k(k为数据类别总数)个类概率向量并将其结果进行合并，分别得到2(n-m1+1)维，2(n-m2+1)维的数据实例.

如图2所示，在级联森林模块中，将粒度扫描模块得到的g维概率向量作为输入，在4个森林中对其进行训练.随机森林使用基尼指数G作为节点分裂指标，其公式为：

(1)

(2)

其中Pt代表第t类的概率，A为数据集D中的某一属性，按照属性A将数据集分为D1和D2.

每个森林生成一个k维的概率向量并与g维的原始概率向量合并作为下一级联层的输入，为了防止过拟合，采用k折交叉验证方法进行训练，交叉验证值β的公式如下：

(3)

其中，n为数据集划分的子集个数，Qi为第i次划分的分类结果.级联层依次迭代，直至达到最大级联层数，将森林中的概率向量的平均值取最大值并作为最终结果输出.

3 基于加权深度森林的离群数据挖掘方法

3.1 基本思想

针对深度森林算法在构建级联森林模块时特征选择的随机性大导致算法的级联层数增加，系统开销大等问题，加权深度森林(WDF)算法重新定义了级联森林模块.为了方便描述该算法，首先给出了如下定义.

定义1.设数据集D={L1，L2，…，Lm}，类别为C={C1，C2，…，Cn}，森林的预测概率矩阵如下：

(4)

其中，Bij表示第i条数据被划分为第j类的概率，根据森林预测概率矩阵中每一行中最大值的列下标作为该条数据的最终预测类别，并将其在矩阵中标记为1，其余为0，例如：

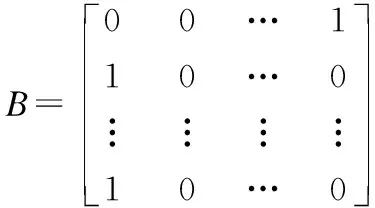
(5)

则在算法中森林的准确率公式如下：

(6)

其中，m表示数据总数，n表示类别数，A[i][j]表示数据样本的实际类别矩阵，B[i][j]表示预测概率矩阵，通过交运算得到每个森林的预测准确率.

定义 2.设森林R={1，2，…，r}，森林的权重因子μ定义如下：

(7)

Pi表示第i个森林的准确率，则第i个森林的类预测概率矩阵为：

B(i)=B×μ

(8)

定义 3.形式背景为二元组，D={Lt|t=1..n}是记录集，C={Cj|j= 1..r}是类集，满足Ci∩Cj=Ø且 ∀Lt∈D→(Lt∈Ci∧Lt∉Cj)(若i≠j)，则孤立因子α可以用公式(9-11)定义：

M(Lt)=min{d(Lt，L1)，d(Lt，L2)，...，d(Lt，Ln)}
(L1，L2，…，Ln∈Ci，t≠n)

(9)

(10)

(11)

在式(9)中，d(Lt，L1)为第t个点与第一个数据点的距离，ρ(Ci)表示第i类数据的类密度[12]，孤立因子α的阈值函数F(r)定义如下：

(12)

其中，r为数据集中的类别数r>0，阈值函数F(r)为单调递减函数，随着r增加，F(r)减小.

基于以上定义，在WDF算法中构建级联森林模块时，首先对森林集成部分进行分析，在算法中用到的随机森林和完全随机森林都是随机选择特征，通过定义1可以得到森林的预测概率矩阵，用公式(6)计算出森林的准确率，并引入定义2中的权重因子μ，对森林的概率结果进行加权.准确率越高，权重因子μ越高，森林权重越大，反之，权重则越小，这一步骤可以有效降低特征随机选择的根节点中无关属性对算法性能的影响.将加权之后的概率向量作为输入进入下一个森林级联层继续训练，重复上述操作，直到达到最大级联层数.在级联加权森林构造完成后，由于样本数据分布的不同，数据被划分为密度不同的类，通过定义3中可以得到每类样本数据的类密度，数据越多的类，其类密度越小，并用公式(11)计算其局部孤立因子α，α越大，数据离群的概率越大.通过公式(12)可以得到在不同数据集中孤立因子函数阈值F(r)，α值大于F(r)的数据则为离群数据.

3.2 WDF算法描述

WDF算法主要包括两部分，第1部分为多粒度扫描部分，第2部分为级联加权森林部分.在多粒度扫描部分中，通过滑动窗口对数据进行扫描，将数据划分为多个不同的维度，并依次进入随机森林和完全随机森林训练，将得到的类概率向量进行合并作为级联加权森林模块的输入.在级联加权森林部分，输入数据进入森林集成部分进行训练，包括两个随机森林和两个完全随机森林.为了避免过拟合，采用公式(3)中的k折交叉验证法进行训练，并采用定义1的方法获得森林的预测概率矩阵，矩阵每一行的最大值所对应的下标作为其预测结果，用公式(6)对森林的准确率进行计算.引入定义2中的权重因子，对森林进行加权，森林的权重因子μ越大，权重值越大.将加权之后的每个森林的概率向量与粒度扫描层的概率结果相结合作为下一层森林级联层的输入，并计算该层的错误率，递归上述操作，直到达到最大级层数，或该层的错误率增加，迭代停止.WDF算法的具体步骤如下.

算法：加权深度森林(WDF)算法

输入：训练集D，样本个数X，测试集W，属性个数A，窗口大小scan_size，最大级联层数T，森林个数4

输出：离群点个数

1. for x=1 to X do

2. win_len = len(A)-scan_size + 1；

3. 读取训练集train_data；测试集test_data；

4. 读取训练集标签train_label；

5. for i=1 to win_len do

7. end for

8. end for

9. for j=1 to 4 do

10. val_prob=np.zeros(len(train_data)，

len(set(train_label))×4))

11. one_result= max(val_prob)

13. result=val_prob(test_data) × μ；

14. end for

15. concatenate(result)；

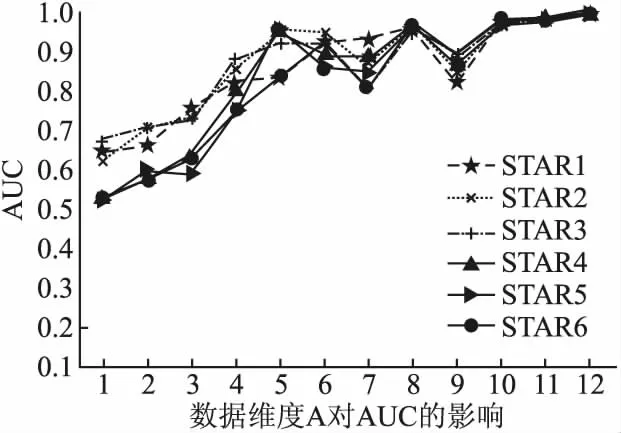
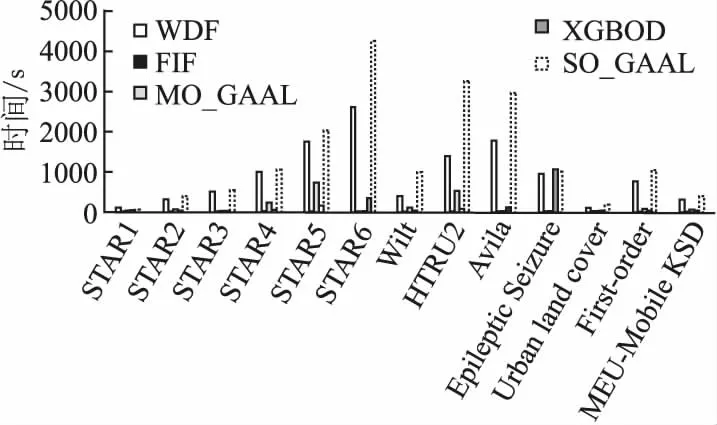
16. if t

17. t=t+1；

18. end if

级联加权森林模块构造完成以后，通过公式(9)-公式(12)对数据集中的每类样本数据计算其孤立因子α以及该数据集的阈值函数F(r)，将α> F(r)的数据作为离群数据.

3.3 算法复杂性分析

本文的算法内容主要包括两个部分，第1部分是数据粒度扫描，第2部分是级联加权森林.对于有n条训练数据，粒度扫描模块的时间复杂度为O(n3)，级联加权森林的时间复杂度为O(n3)，算法的整体时间复杂度为O(n3).改进算法与深度森林算法都不涉及距离的计算，且改进算法减小了可能对离群点检测产生错误影响的森林的权重，有效地减少了系统开销.

4 实验分析

本文利用UCI数据集和恒星光谱数据集进行实验，对本文提出的加权深度森林的离群数据挖掘算法进行验证，实验配置为Intel core i5-4210H，64位操作系统PC机，编程环境python3.7.

4.1 UCI数据集

为了验证WDF算法的有效性，实验中采用了UCI数据集进行实验，数据集的属性信息如表1所示.Epileptic Seizure数据集是癫痫发作病例检测数据，类别2、3、4、5为非癫痫发作者，视为正常数据，类别1为癫痫发作者，视为离群数据.HTRU2[13]数据集是脉冲星候选样本数据，由两种类别构成，实验中将数量相对较少的第2类数据视为离群数据.Wilt[14]数据集是高分辨率遥感数据，数据集中第2类数据有261个样本约占5.3%，视为离群数据.Avila[15]数据集是Avila Bile图像数据，将数据量相对较少的W、C、B类数据作为离群数据.Urban land cover数据集是土地覆盖数据，将数据量较少的土地覆盖类型soil、pool类组合作为离群数据，约占9.33%.First-order数据集是包含51个维度的一阶定理证明数据，本实验去除了5个分类属性，共46个属性，将未能证明定理的第2类数据作为离群数据.MEU-Mobile KSD数据集是触摸移动设备的动态数据，共有56个类别，将54、55、56类组合作为离群数据.

4.2 LAMOST恒星光谱数据集

实验中使用的恒星光谱数据是由郭守敬望远镜(LAMOST)巡天探测获得，每条光谱数据都有其对应的波长与流量，波长范围约在3700-9000，根据其表面温度及谱线的不同，恒星被分为O、B、A、F、G、K、M这7大类.

式中，Dx、Dy分别为泥沙扩散系数沿x、y方向的取值；S为含沙量；s F 为底部冲刷函数，采用切应力理论表达式如下：

光谱数据的维度很高，但并不是所有的属性都是我们所需要的，使用基于相关子空间[16]的特征选择方法可以有效地解决高维数据的处理问题，相关子空间βij公式如下：

(13)

公式(13)所示，δij表示局部密度差异因子，α表示局部密度差异因子的阈值，当局部密度差异因子小于阈值时，第j维特征加入相关子空间中.每条属性的特征强度通过Lick系统中线指数[17]的等效宽度(EW)来获得，公式如下：

(14)

λ1和λ2表示中心波段的起始波长和终止波长，FIλ表示在中心波段单位波长的流量，FCλ表示中心波段连续谱的流量.通过数据预处理，高维的恒星光谱数据被处理为12维，数据类型为连续型，恒星数据集的属性信息如表1所示.

表1 选择的数据集Table 1 Selected data sets

从LAMOST DR5中获取了6个不同数量的恒星光谱数据集，数据的具体属性如表1所示.STAR1、STAR2和STAR3数据集的训练数据样本由F类型的恒星光谱与异常类型数据两部分组成，将非F类数据视为离群数据.STAR4、STAR5和STAR6数据集的数据样本由恒星光谱数据与异常数据两类数据组成.恒星光谱数据中包含A、F、G、K、M 5种不同类型的光谱数据，其数据分布为平衡数据，非恒星光谱数据视为异常数据.

4.3 参数分析

为了验证窗口大小、决策树数量对本文算法性能的影响，从表1的数据集中选择了4个数据集进行测验，分别为STAR 4、STAR 5、HTRU2和Avila数据集.采用AUC作为评估标准，并画出了ROC曲线，AUC计算公式如下：

(15)

(16)

其中P1表示正常样本的预测概率，P0表示异常样本的预测概率，M、N分别为正常、异常样本的个数.ROC曲线下方围成的面积即为AUC，AUC的值越接近1，说明算法的性能越高，检测效果越好，反之，则越差.

4.3.1 窗口大小X对AUC的影响

本实验采用不同的数据集对滑动窗口大小X进行了实验，实验结果如图3所示.在不同的数据集中，当滑动窗口为(1，2，1)和(2，2，1)时，算法的性能相对较低，可能的原因是窗口数太小，无关属性作为主要特征的概率增加，离群点检测的错误率增大.随着滑动窗口数的增加，当窗口大小为(4，2，2)和(8，4，2)时，不同数据集的AUC值都随之增加，并且从图中可以看出，当窗口大小为(3，4，6)和(10，3，5)时，在不同的数据集中，该算法AUC值最高且接近于1.由于本算法第1部分是滑动窗口粒度扫描模块，第2部分是级联加权森林模块，窗口大小X对算法中离群点特征判断具有重要影响，并且在HTRU2数据集中数据维数为8，因此窗口大小X选作(3，4，6)，不仅可以避免因属性特征较少对离群点特征造成的错误判断，还能减少大数据量产生的系统开销.因此，在后续实验中将窗口大小X的默认值设定为(3，4，6).

图3 窗口大小X对AUC的影响Fig.3 Influence of window size X on AUC

4.3.2 决策树的数量T对AUC的影响

该实验采用与4.3.1节相同的方法，对不同的决策树的数量T进行实验，结果如图4所示.随着决策树数量T的增加，该算法在不同的数据集中的AUC值也随之增加，且在T为100时，算法的AUC值逐渐收敛且趋于稳定，接近于1.当决策树的数量T小于50时，不同数据集的AUC值差距较大，可能的原因是决策树数量较少，在森林特征随机选择过程中，主要特征被作为根节点的概率较低，导致算法的AUC相对较低.当子树数量T为50时，AUC值开始趋于收敛，并且当T为100时收敛达到最大值，随着决策树中数量T的增加，当T数量为200、400、800时，在不同的数据集下，算法的AUC值都接近于1.由于森林中子树的数量太多会增加算法在时间和空间上的消耗，增加系统开销.并且从多次实验中可以看出，决策树的数量T为100-400范围时，在不同数据集中，算法的整体性能较为稳定且精度较高，且算法开销也较低，在该实验中使用T=100作为后续实验的默认值.

图4 子树的数量T对AUC的影响Fig.4 Influence of the number of subtrees T on AUC

4.4 实验结果分析

本节主要内容是通过与4种不同的离群点检测算法进行AUC值和ROC曲线对比，来验证该算法的性能.

4.4.1 各对比算法的AUC

本节采用光谱数据对5种离群点检测算法进行对比，WDF算法的参数设置如4.3小节所述.快速隔离森林算法(FIF)通过计算数据在每个隔离树中的平均高度来判断离群数据，MO_GAAL和SO_GAAL[18]算法采用对抗性学习模型来检测异常点，XGBOD[19]算法是一种基于无监督的异常点检测方法.

表2表示了在不同的数据集中各对比算法的AUC，其中黑体部分为这些数据集中最高的AUC值.在本实验所采用的

图5 各算法的ROC曲线Fig.5 ROC curve of each algorithm

数据集中，WDF算法和XGBOD算法的AUC值相比于FIF、MO_GAAL、SO_GAAL算法较高，并且由表2可知，WDF算法的性能更加稳定，在光谱数据的离群点检测中，WDF算法相比其它几种离群点检测方法具有更高的AUC值，原因是在级联森林模块中，采用加权森林的方法对数据特征进行概率计算，与传统方法相比减少了低准确率森林对异常数据特征判断的干扰，使得离群数据检测具有更高的可信度.

表2 对比算法的AUCTable 2 AUC of the comparison algorithm

图5表示了各算法在3个代表数据集中的ROC曲线，其中dash-dot线为本文的算法，从图中可以看出，WDF算法在不同的数据集中ROC曲线下的面积均大于其余的对比算法，且算法性能较为稳定.在Wilt和STAR5数据集中，WDF算法的ROC面积远远超过了其他算法的ROC面积，并且AUC值几乎接近于1.在Avila数据集中，WDF算法的ROC值仅低于XGBOD算法，XGBOD算法对于维数较低的数据集效果更加明显.SO_GAAL算法与MO_GAAL算法在整体性能上表现较差，可能的原因是在生成模型中，离群数据的特征较不明显，与正常数据差距较小，导致算法性能较低.

4.4.2 不同数据维度对算法的影响分析

图6展示了不同维度的恒星光谱数据集在加权深度森林算法中的结果，随着数据维度的增加，算法的AUC值整体呈上升趋势，直到维度数为5时增长发生波动.当数据维数为6-10之间时，算法的AUC值变化幅度较大，可能的原因是在这些维数中包含了无关属性，从而导致在森林特征随机选择过程中，无关属性被选择的概率较大，AUC值较低.当维数为10-12之间时，不同的恒星光谱数据集中算法的AUC值都在0.9以上，并且当维数为12时，不同数据集的AUC值基本都收敛于最大值1.因此在光谱数据集中选择维数为12，既能保证算法具有较高的效率，同时可以避免因维数较小，某些明显特征点被忽略.

图6 数据维度A对AUC的影响Fig.6 Impact of data dimension A on AUC

4.4.3 算法的运行时间

图7表示了WDF算法与4个对比算法在各个数据集中运行时间的对比结果，在6个光谱数据集中，随着数据量的增加，各个算法的运行时间也依次增加.在WDF算法中，随着数据量不断增加，在多粒度扫描模块中每个森林中子树的个

图7 算法的运行时间(s)Fig.7 Run time of algorithm(s)

数较多，导致其在进行特征转换时所需要的时间也增加.在级联森林模块中通过引入权重因子减少了特征随机选择导致的算法误差，与4个对比算法相比，WDF算法的运行时间并不是最少，相比于FIF、MO_GAAL算法消耗时间较长，但WDF算法在离群点检测中的精确率更高，能够更加准确的对离群点进行检测，整体而言WDF算法在离群点检测方面具有更高的挖掘质量.

5 结束语

本文提出了一种基于加权深度森林的离群数据挖掘算法，该算法采用森林加权的方式，通过计算森林的准确率引入加权因子μ，赋予森林不同的权重值，准确率越高，μ越大，权重值也越大，降低了森林特征随机选择对算法性能的影响，有效地提升了算法的整体性能；通过类密度引入了局部孤立因子α及其阈值函数F(r)，α值大于F(r)的数据视为离群数据，使算法在不降低效率的情况下提高了离群点挖掘的准确性.采用UCI数据集和恒星光谱数据集验证了算法的有效性.本文下一步的研究方向为考虑如何能提高算法的运行速度，以实现海量数据离群点的快速检测.