基于转向补偿的车辆纵向坡度估计

李林润 张建 姜洪伟 刘秋铮 王宇

（1. 中国第一汽车股份有限公司智能网联开发院，长春 130013；2. 汽车振动噪声与安全控制综合技术国家重点实验室，长春 130013）

主题词：纵向坡度估计 侧向加速度估计 卡尔曼滤波 转向补偿

EPS Electric Power Steering

ABS Antilock Brake System

ESP Electronic Stability Program

1 前言

汽车智能化与电动化的发展对纵向运动控制、主动安全控制和能量回收等功能提出了更高要求。重力在倾斜路面下产生的纵向分量会显著影响车辆纵向动力学特性，进而影响上述功能的控制效果。以车辆右手坐标系为基准，重力纵向分量取决于车辆平面下的路面倾斜程度，即车辆纵向坡度(Grade)。因此，实时稳定获取车辆纵向坡度，确定重力纵向分量对提升智能电动汽车的诸多控制系统性能具有实际意义。

目前常见的纵向坡度获取方法可以被划分为基于信号处理技术的传感器信息时频分析方法和基于汽车运动状态模型的估计方法。前者主要使用各种传感器信息，通过滤波处理、几何关系计算等方式实现对路面倾角的直接测量，该类方法一般需要加装额外的传感器，成本较高，实际应用困难。后者根据所用运动状态模型，分为基于动力学模型的方法和基于运动学模型的方法：动力学方法利用车载CAN 网络中的力信号与车速信号构建包含车辆纵向坡度的纵向动力学观测器，利用最小二乘参数辨识算法或卡尔曼滤波最优估计方法实现路面坡度的实时准确估算。该类方法需额外处理制动、换挡特殊工况，且模型参数受高频噪声影响较大，易导致估值不稳定。运动学方法主要利用固定于车身上的纵轴加速度传感器，构建包含重力加速度纵向分量的纵向运动学观测器，其状态空间方程简单，采用卡尔曼滤波最优估计方法可实现路面坡度的实时准确估算。此类方法易于调试、计算量小并且落实成本低，广泛应用于实际工程当中。

基于汽车运动状态模型的车辆纵向坡度估计方法的效果取决于模型精度，传统的单自由度纵向运动学模型忽略了车辆在转弯工况下的横纵向耦合特性，未考虑车辆侧向与横摆运动对纵向运动状态的影响，造成观测器模型失真，导致车辆在倾斜路面转弯或掉头工况下，纵向坡度估计偏差较大。

本文针对该问题，提出基于转向补偿的车辆纵向坡度估计方法：分析车辆转向时侧向与横摆运动对纵向运动的耦合影响机理；根据车辆二自由度动力学模型设计侧向速度观测器；设计基于运动学的卡尔曼滤波纵向坡度估计算法，使用横摆角速度与侧向速度观测对车身纵轴加速度信号进行校正补偿，最终实现了车辆横纵向耦合工况下的纵向坡度可靠估计。

2 算法整体架构

本文提出的基于转向补偿的车辆纵向坡度估计算法整体架构如图1所示。

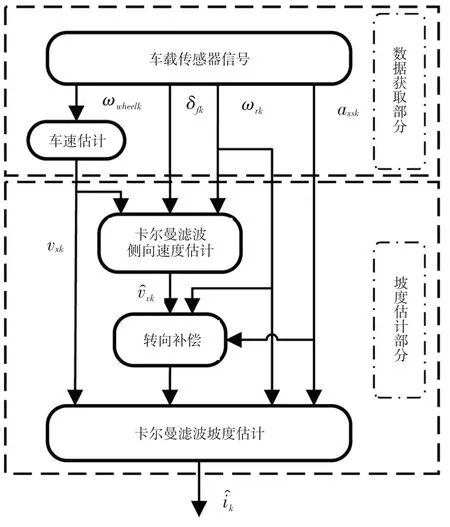
图1 转向补偿纵向坡度估计算法架构

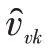
3 车辆状态耦合分析与建模

车辆转弯工况下的横纵向状态之间存在较强相关性，分析其耦合机理是准确建立状态观测模型的基础。

3.1 横纵向运动耦合特性分析

图2 为车辆转弯工况下的瞬态运动学过程，其中为固定于地面的坐标系。xOy为固定于车辆的坐标系，坐标原点位于车辆的质心O，其中代表车辆纵向，代表车辆侧向，横摆方向取逆时针为正。矢量代表车辆质心O在大地坐标系中的位置矢量。

图2中，O点的速度矢量可以表示为：

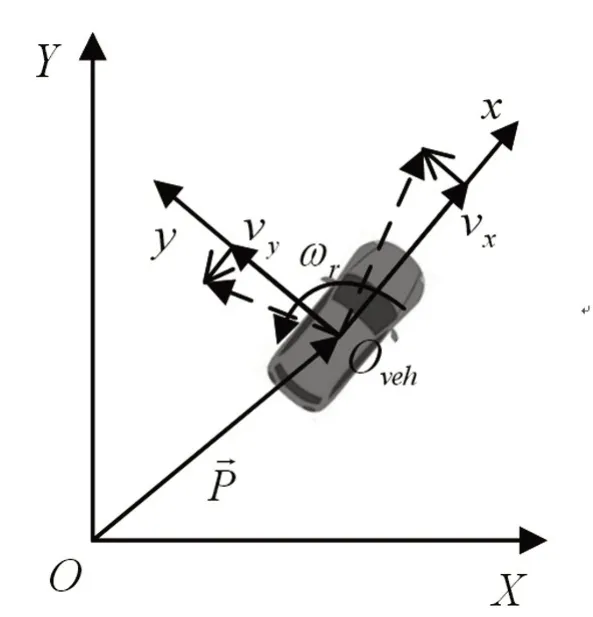
图2 车辆转弯运动学示意

式中，和分别表示轴和轴方向的单位矢量；v和v分别表示车辆在和两个方向上的速度分量。

上式进一步对时间求导可得O点的加速度矢量，如式（2）所示：

3.2 考虑转向补偿的纵向运动学模型

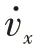
图3 纵轴加速度信号模型

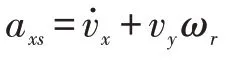
由于车辆纵向坡度的实际变化速度相较采样时间和车辆动力学状态变化缓慢，因此其导数可近似为0。

3.3 侧向速度估计模型

准确获取横摆角速度ω和侧向速度v是校正补偿的前提，前者可以通过车载传感器直接获取，后者需采用基于模型的估计方法获取，用于估计的侧向动力学模型如图4所示。

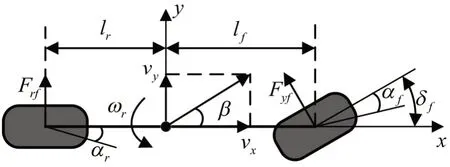
图4 二自由度车辆动力学模型

根据该模型的车轮小角度转动假设，建立车辆动力学平衡方程。

轮胎侧向力可以通过线性轮胎模型表示。

式中，α和α分别为前后轮胎侧偏角；C和C分别为前后轮胎侧偏刚度。

联合式（7）、式（8）最终得到二自由度车辆动力学方程为：

4 考虑转弯补偿的纵坡卡尔曼滤波估计

4.1 卡尔曼滤波方法

卡尔曼滤波算法能够根据当前时刻离散状态方程的预测值、离散观测方程的观测值与上一时刻离散的最优估值，通过不需要存储历史数据的递推过程，计算出新的最优估计，利用有限的、不直接的测量信息实现目标参数的实时估计。

该算法具体包含2个更新过程，共5个步骤，整体流程如图5所示。

图5 卡尔曼滤波道路坡度估计算法流程

时间更新过程包含如下2个步骤：

（1）状态预测：通过上一时刻的最优估值计算当前时刻的预测状态，具体如式（10）。

（2）协方差预测：通过上一时刻的最优估值误差协方差计算当前时刻预测状态的误差协方差，具体如式（11）。

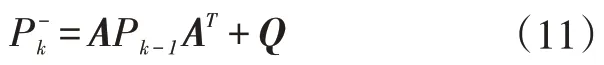
测量更新过程包含如下3个步骤：

（1）卡尔曼增益计算：通过当前时刻预测状态的误差协方差和测量噪声协方差来计算卡尔曼增益，具体如式（12）。

式中，为观测矩阵；测量噪声协方差。

（2）状态更新：通过当前时刻的预测状态、测量值和卡尔曼增益计算最优估值，具体如式（13）。

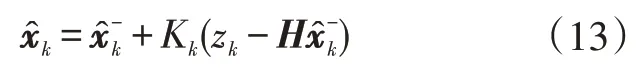
式中,为系统状态观测。

（3）协方差更新：通过当前时刻预测状态的误差协方差和卡尔曼增益计算最优估值误差协方差，具体如式（14）。

将系统模型离散化带入式（10），并设定系统初始参数后，反复迭代上述5个步骤，即可实现基于卡尔曼滤波的状态估计。

4.2 侧向速度的卡尔曼滤波估计

将式（9）离散化，得到用于卡尔曼滤波估计的状态预测和测量式（15）。

将式（15）带入上述卡尔曼滤波递推式（10）～式（14），并设定系统初始参数，即可实现侧向速度的实时估计，并将其用于纵向坡度估计的转向补偿。

4.3 车辆纵向坡度的卡尔曼滤波估计

将考虑转向补偿的纵向运动学模型式（6）离散化，结合上述侧向速度估计值，得到用于卡尔曼滤波估计的状态预测和测量方程式（16）。

将式（16）带入上述卡尔曼滤波递推公式，并设定系统初始参数，即可实现车辆纵向坡度的实时估计。

5 测试验证

5.1 仿真测试验证

利用MATLAB∕Simulink 编写考虑转弯补偿的路面坡度估计算法，并利用CarSim提供的车辆动力学模型和仿真场景，进行联合仿真验证。

与本算法相关的仿真车辆参数如表1 所示，均与后续实车参数对应。

表1 仿真车辆参数

考虑基于式（6）的坡度估计原理简单，其状态预测方程相对精确，因此过程噪声协方差矩阵较小。由于式（9）中部分参数不易准确获取，且二自由度模型本身存在一定简化，因此侧向速度估计的过程噪声协方差矩阵相对较大。测量更新过程中，传感器精度较高，测量误差小，因此测量噪声协方差均较小，最终得到的算法预设参数如表2所示。

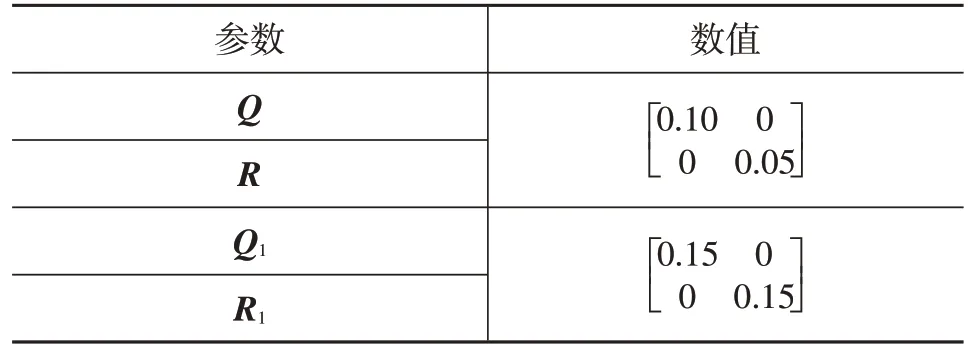
表2 算法预设参数

设置仿真车辆期望行驶路径如图6 所示，以此为基础设置2种仿真道路。

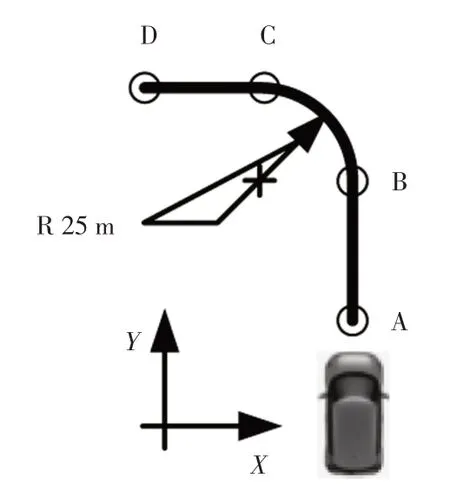
图6 仿真工况示意

（1）道路倾斜方向（纵向坡度角）沿期望路径保持不变，如图7(a)所示。此工况用于分析车辆侧向运动对纵向坡度估计结果的直接影响，也可以反应山区道路的坡度设置情况。

（2）道路倾斜方向固定，如图7(b)所示。此工况下，AB段车辆纵向坡度角与道路倾斜角度一致，BC段车辆纵向坡度角逐渐减小，CD段为0。该工况可以体现车辆在坡道上掉头时，车辆纵向坡度角沿期望路径变化的情况。

图7 仿真道路示意

设置道路倾斜程度=0.1，车速保持36 km∕h，单位采样时间=0.001 s，得到如图（8）所示的仿真结果。

由于纵轴加速度传感器固定于车身上，基于运动学的纵向坡度估计算法实质是对车身俯仰角的估计。当车速稳定时，俯仰角波动较小，能够较好反映纵向坡度，因此仿真阶段以车身俯仰角为真值，保证了与实车测试真值对应。图（8）中实际值的波动是由于CarSim 软件内置的车速控制模块引起的实际车速波动导致，但是由此导致的车身俯仰角波动幅度在0.007 rad 以内，远小于车辆所处的坡道纵向坡度。

道路1 的倾斜方向随期望路径航向实时变化，车辆纵向坡度始终为0.10 左右，如图8(a)中实线所示。在里程 50～110 m 时，车辆处于图 6 中 BC 段，转向运动导致基于直线运动学的纵向坡度估计方法失真，未进行转向校正的纵向坡度估计误差较大，与实际值的最大绝对误差为0.022 1，与实际值均值的最大相对误差为21.5%；而校正后的估计误差明显减小，最大绝对误差为0.001 9，最大相对误差仅为1.86%。

图8 0.10坡道纵向坡度估计结果对比

道路2的倾斜方向不随路径变化，车辆处于AB段时车辆纵向坡度始终等于道路倾斜程度，当车辆处于BC段时，车辆纵向坡度随行驶航向逐渐变小，直到车辆处于CD段，道路倾斜方向与车辆轴重合，完全处于侧坡工况，车辆纵向坡度为0，具体实际值变化如图8(b)中实线所示。在里程50～110 m 时，车辆处于BC 段，转向运动导致状态空间方程（1）失真，未校正的估计误差较大，与实际值的最大绝对误差为0.024 2,与实际值均值的最大相对误差为37.4%；而校正后的估计误差明显减小，最大绝对误差为0.002 4，最大相对误差为3.75%。

为进一步说明该校正方法的有效性，多次更改坡度进行仿真，统计得到道路1和道路2下的误差如表3和表4所示。可见本文提出的侧向运动补偿方案能够有效提高车辆转弯工况下的坡度估计精度。

表3 道路1估计误差对比统计表

表4 道路2估计误差对比统计表

5.2 实车测试验证

实车验证阶段，将所开发算法嵌入到以dSPACE MicroAutobox 为原型控制器的实车测试平台上。控制器通过CAN 总线实时采集原车电动助力转向系统EPS 的方向盘转角信号，制动防抱死系统ABS 的纵向车速信号，车身稳定控制系统ESP 的纵轴加速度和横摆角速度信号，实现车辆纵向坡度估计，通过RT3000 组合惯导装置获取车身俯仰角，作为纵向坡度真值。具体的实车测试平台系统架构与实车布置图如图9、图10 所示。测试在一处郊区道路上进行，道路坡度最大在0.05，实际行驶轨迹如图11 所示。

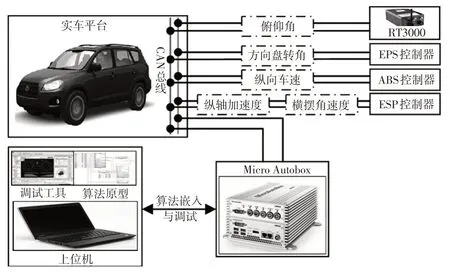
图9 实车测试平台系统架构

图10 实车布置

图11 车辆实际行驶轨迹

轨迹前半段进行了直线行驶工况对比测试，如图12所示。由测试结果可以看出，本文提出的纵向坡度估计算法计算结果稳定，且与实际值基本相符，平均估计误差能够保持在0.01以内，证明了该算法在直线行驶工况中的有效性。

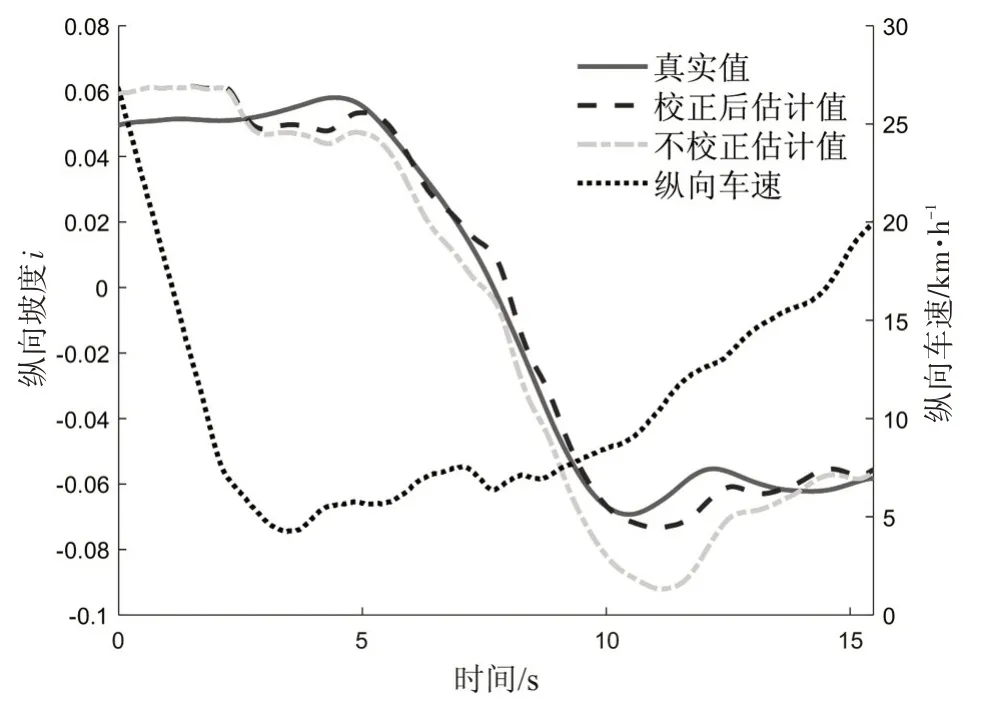
图12 直线行驶工况测试

为进一步说明本文提出的侧向运动补偿算法的有效性，轨迹后半段进行了坡道转弯行驶工况对比测试，结果如图13所示。

图13 转弯行驶工况对比测试

由图13(a)可知，车辆在当前测试场景完成了横纵向耦合程度较高的掉头工况，整个过程坡度变化量较大，能够较好地证明本文算法的效果。由图13(b)的对比结果可知，当车辆横摆角度较大时，如图中7～13 s所示，未加入校正算法的估计结果将出现较大的超调，最大误差约为0.03，失去准确性。校正算法的加入能够保证车辆转弯工况下的坡度估计精度，减小超调现象，最大误差约为0.01，减小了66.7%，证明了本文提出算法的有效性。

6 结束语

为提高利用车身纵轴加速度信号所设计的纵向坡度估计算法的鲁棒性，考虑车辆转向行驶工况，对车辆侧向运动学进行数学分析，揭示了车辆实际纵向加速度与侧向运动特征的耦合关系。设计了基于车辆侧向动力学的侧向速度卡尔曼滤波算法，为车身纵轴加速度信号提供实时的数值补偿，并最终设计了基于车辆纵向运动学的纵向坡度卡尔曼滤波估计算法。

进行了2 种典型道路下的多次仿真对比试验，并对估计误差进行了统计分析，相对误差和绝对误差均有明显降低，证明了所提出方法在车辆转弯时的有效性。在大坡度道路上分别进行了直线与掉头工况的实车测试：在直线行驶工况下，平均估计误差保持在0.01 以内；在转弯工况下，估计结果的超调量相较于未进行转向补偿的传统估计算法，超调量降低了66.7%，最大误差约为0.01。测试结果证明了基于转向运动补偿的纵向坡度估计算法能够有效克服传感器噪声，并在车辆转弯行驶的过程中获得更好的估计结果。

下一步研究将进一步考虑车辆急加速、急减速和换挡时纵向加速度剧烈变化工况下的车辆纵向坡度估计问题，进一步提高算法的特殊工况适应性。