流量测验误差分析及对推求设计洪水的影响

外力·阿合买提

(新疆维吾尔自治区水文局水文实验站，新疆 乌鲁木齐 830049)

0 引言

流量是反映水资源和江河湖库等水体的水量变化的基本资料，是综合开发利用水资源的一项重要基础资料，是各河流最重要的水文特征值。在进行流域水利规划，各种水工建筑物的设计施工、管理运用、防洪调度、抗旱减灾、水资源利用及保护以及水质监测等诸多方面都需要流量资料[1]。通过研究流量误差来源与误差规律性，在实际工作中减小和尽可能地消除误差，以得到精确的测验结果，这不但对水资源开发利用的相关设计具有重要意义，其对于水文测验科学技术水平的提高和发展也是非常重要的。

在进行水文分析、计算设计洪水值时，通常是对特大洪水的流量值予以高度重视，而对流量测量的误差特别是中、低水流量的测量误差较少地进行系统的考虑，不可否认特大洪水的流量值在适线中的重要性，但考虑流量测量的误差特别是中、低水流量的测量误差对设计洪水可能产生的影响，对推求更为准确的设计洪水值将会有所帮助[2]；另一方面，知道对推求设计洪水值产生影响的流量测验误差的极限值，可以在制定测站测流方案时予以考虑，在保证测验精度的情况下，选择较为经济的测流方案。目前，国内对流量测验误差对推求设计洪水值的影响的研究较为少见。本论文通过对流量测验误差进行分析，进一步研究测验误差对推求设计洪水的影响，使流量测验工作能更好地为防洪减灾及水工建筑物的防洪设计工作创造条件。研究成果对水文测站制定既经济又能保证测验精度的测流方案提供了依据，对水文分析工作中设计洪水的计算成果更符合实际创造了条件。

1 研究方法

一个水文原始数据(水文变量)都是由真值和原始误差组成，以流量为例，则有：

Q=q-ε

(1)

式中：Q为含有原始误差的流量实测值；q为相应于流量实测值Q的真值；ε为相应流量实测值Q的原始误差。

流量实测值Q的相对误差可用来表示：

α=(Q-q)/q

(2)

式中：α为相应流量实测值Q的相对误差。

原始数据相对误差大小由相对误差的均方差来表示，某种误差的均方差可假定为常数。而相对误差的均值可假定为0，则：

(3)

式中：σα为相对误差的均方差。Eα为相对误差的期望值。

流量原始误差ε与实测资料流量Q和相应于流量实测值的真值q均有关，不能视为相互独立。而相对误差α的大小与真值q的大小无关，α与真值q可视为相互独立的。由公式(2)推出：

Q=q+α·q

(4)

EQ=Eq+E(αq)=Eq+Eα·Eq=Eq·(1+Eα)=Eq

(5)

式中：EQ为实测资料Q的数学期望；Eq真值q的数学期望。

Q的2阶中心矩可以由下式表示：

μ2Q=E(Q-EQ)2=E(q+αq-Eq)2

=E(q-Eq)2+2E[(q-Eq)αq]+E(αq)2

(6)

由公式(6)可得：

μ2q=[μ2Q-σ2(EQ)2]/(1+σα2)

(7)

式中：μ2Q为Q的2阶中心矩；μ2q为q的2阶中心矩；v2qq的2阶原点矩。

同理可得Q的3阶中心矩和q的3阶中心矩：

μ3Q=E(Q-EQ)3=E(q+αq-Eq)3

=E(q-Eq)3+3E[(q-Eq)2αq]+3E[(q-Eq)α2q2]+E(αq)3

=μ3q+3E[(q3-q2Eq)α2]+E(αq)3

=μ3q+3Eα2(v3q-v2qEq)+Eα3v3q

(8)

式中：μ3Q为Q的3中心矩；μ3q为q的3阶中心矩；v3qq的3阶原点矩。

因为α与q相互独立，则f(α)与f(q)相互独立，所以：

E[(q-Eq)α]=E(q-Eq)Eα=0

(9)

E[(q-Eq)αq]=E[(q-Eq)q]Eα=0

(10)

E(αq)=EαEq=0

(11)

(12)

E[(q-Eq)2αq]=E[(q-Eq)2q]Eα=0

(13)

E[(q-Eq)α2q2]=E[(q-Eq)q2]Eα2

(14)

E(αq)3=Eα3Eq3=Eα3v3q

(15)

假定Q为偏态分布(P一Ⅲ型分布)，则资料的原始误差ε一般为偏态分布(假定为P一Ⅲ型分布)，可假定其均值为零Eε=0，从而没有Cvs值，这样它有两个统计参数σε和Csε。ε的偏态系数Csε的近似公式可由下式表示：

(16)

(17)

(18)

式中：σε为原始误差的均方差；CSε为原始误差的偏态系数；μ3ε为原始误差的3阶中心矩。

相对误差α的3阶原点矩Eα3可由原始误差ε和真值q的参数求得。

μ3ε=Eε3=E(αq)3=Eα3Eq3=Eα3v3q

(19)

则Eα3为：

(20)

(21)

将公式(21)代入公式(20)中得：

(22)

将公式(22)代入公式(8)中得：

μ3Q=μ3q+3σα2[μ3q+3μ2qEq+(Eq)3-v2qEq]+Csεσα3v2q3/2

(23)

μ3q={μ3Q-3σα2[3μ2qEq+(Eq)3-v2qEq]-Csεσα3v2q3/2}/(1+3σα2)

(24)

由公式(7)可得：

(25)

由公式(24)得：

={μ3Q-3σα2[3μ2qEQ+(Eq)3-v2qEq]}

-Csεσα3v2q3/2}/[(EQ)3Cvq3(1+3σα2)]

(26)

式中：Cvq为q的离均系数；Csq为q的偏态系数。

其中Eq=EQ，v2q=μ2q+(Eq)2=μ2q+(EQ)2则可由公式(7)表示成Q的函数，Csε、Cvq可分别由(16)、(17)、(25)式表示成Q的函数。由公式(5)、(25)和公式(16)可看出，真值q的三个参数Eq、Cvq、Csq均可由含有误差的原始资料的三个参数EQ、CVQ、CSQ和表示相对误差的大小σ。求出将q与Q的参数由于相对误差σα的大小不同而引起的差异做一比较，见表1。计算中EQ和Eq均取相对值1。

由表1可看出实测值的CVQ系统偏大于真值的Cvq即CVQ>Cvq，随相对误差σα的增大，其差别愈大。这是因为Q含有误差，使实测资料的离散程度更大了[3]。实测资料的CSQ系统偏大于真值的Csq，即CSQ>Csq，并随相对误差σα增大，其差异明显增大。所以相对误差σα的大小对偏态系数将产生较大的影响。

表1 原始资料Q和真值q参数对照表

由实测资料推求设计洪水，因为资料原始误差的大小不同，所推求的设计值也不相同[4]。为了分析因相对误差所推求的设计值真值进行比较，本文分别采用不同的σα和Cvq、Csq。分别计算出CVQ、CSQ的均值和均方差，并用式(27)求出设计频率下的Qp和qp值，见表2，同时进行相对误差分析，计算结果如表3所示。误差计算公式见公式(2)。

(27)

计算结果表明，在用实测资料推求设计洪水(P较小时)，由于资料的误差一般会使所推求的设计洪水值Q，大于真值q，；资料相对误差的均方差盯。越大， Q，偏大越多；p越小，Q，偏大越多。同时由表3可以看出，设计值的均方差的相对误差更小。可以看出由于资料误差而使所推求的设计洪水偏大不到3%，所以我们可以得出如下结论：因流量资料测验误差对推求设计洪水影响较小，在推求设计洪水时可不考虑该误差的影响。但我们还是应尽量减少水文测验资料的误差，以提高资料测验的精度。

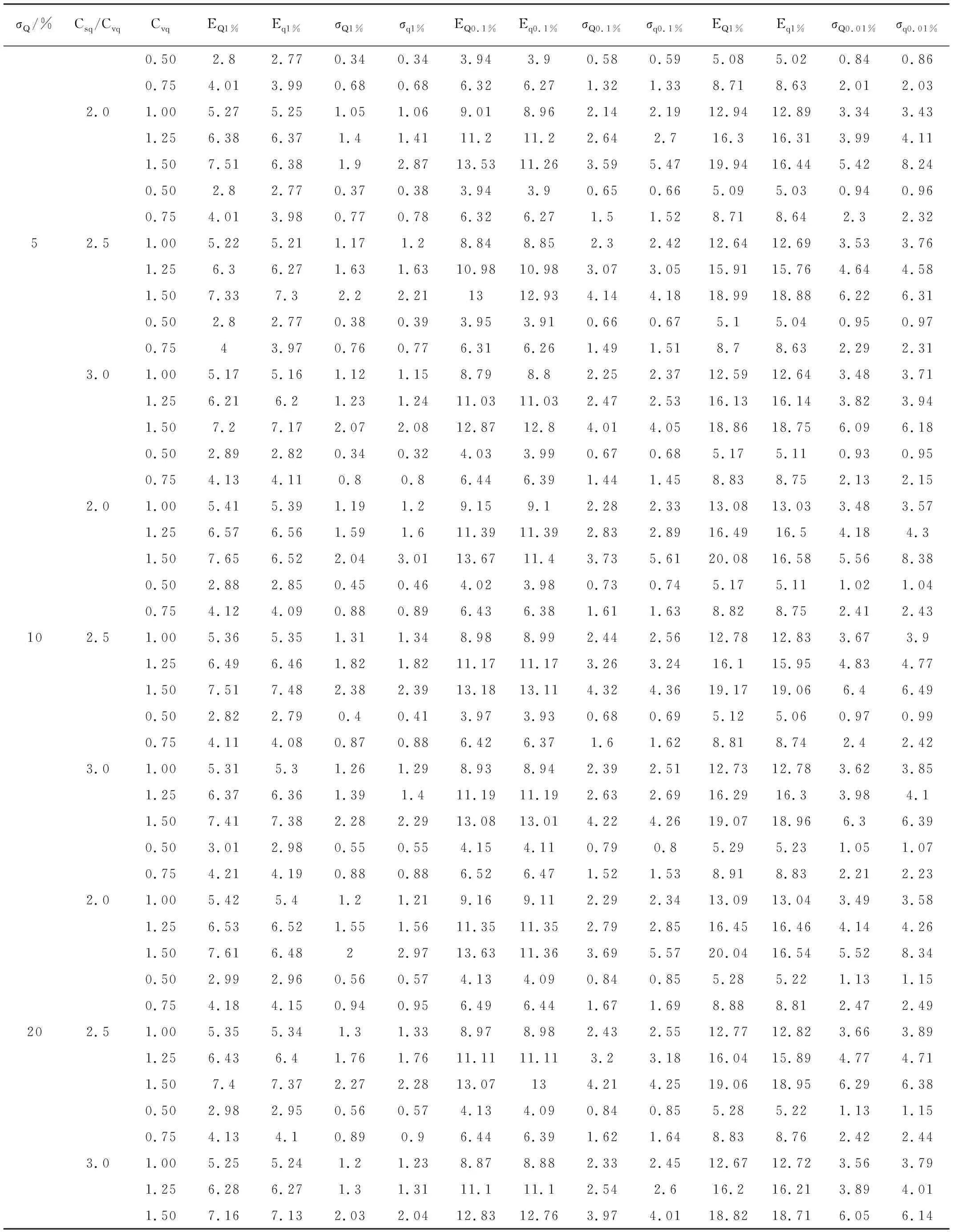
表2 流量真值q和实测流量Q设计值及其统计参数计算表

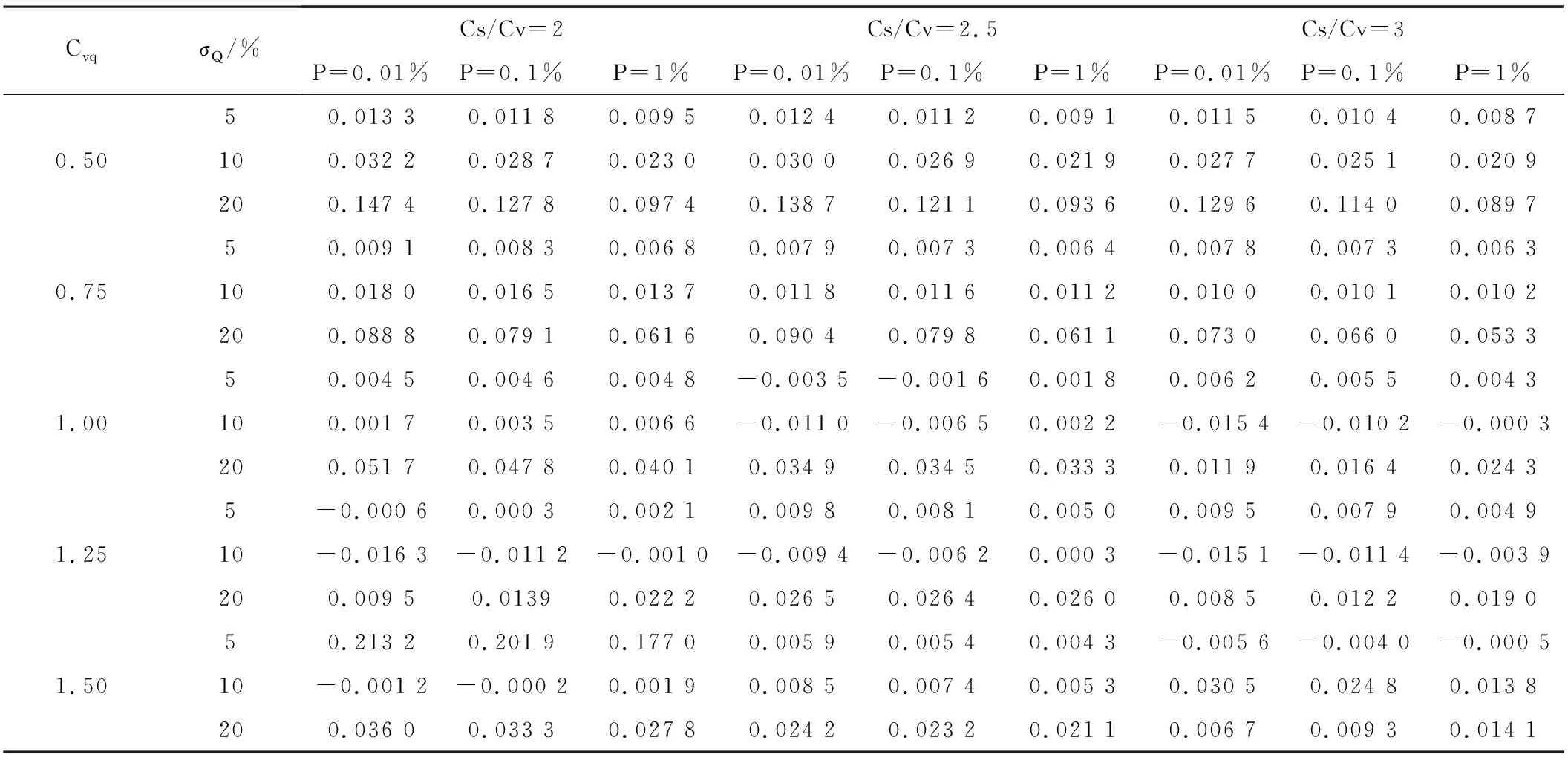
表3 设计值相对误差表

2 结语

流量是综合开发利用水资源的一项重要基础资料，通过研究其误差来源与误差规律性，在实际工作中减小和尽可能地消除误差，以得到精确的测验结果，这不但对水资源开发利用的相关设计具有重要意义，其对于水文测验科学技术水平的提高和发展也是非常重要的，对于流量测验误差的认识和处理，是正确地评价和合理地使用流量测验技术和获得既经济又精确的测验成果的基础。