重本夯基 追本溯源 固本开新
——一道只用直尺(无刻度)作图题的解题分析及思考
石先兵
(福建省福州第一中学,福建 福州)
笔者近期参与了本地区九年级多校联合考试数学试卷的阅卷工作,批改的是一道几何解答题,共两小问。第(1)问源于课本,考查用“边边边”证明两个三角形全等,第(2)问考查用无刻度直尺作图。两小问的组合考查基于核心素养,全方位考查学生对几何知识的综合应用能力,引起笔者强烈的研究兴趣。
一、题目呈现
(1)图1 是一个测角仪器,其中MA=NA,MC=NC。现将点A 与角的顶点重合,AM 和AN 沿角的两边放下,沿AC 画出射线AP,试证明射线AP 是这个角的平分线。

图1
(2)图2 是10×7 的方格纸,纸中每个小方格都是完全相同的正方形,∠EOF(点O 在格点上)画在方格纸上,请利用格点和无刻度直尺作出∠EOF的角平分线。

图2
二、特色解读
(一)源于教材,高于教材
本题第(1)问源于人教版八年级上册第十二章全等三角形中12.3“角平分线的性质”的思考,由角平分仪的工作原理引入作一个已知角的角平分线的依据:由“边边边”判定两个三角形全等从而得到角平分线,也为第(2)问用无刻度直尺作图提供了方向——通过构造全等三角形(边边边)寻找角平分线。第(2)问是要求在方格纸中用无刻度直尺作出角平分线,考查学生的迁移能力和应用意识,除了要知道格子中隐含的几何元素的关系:线段的位置关系(平行或垂直)和数量关系(相等),还要从已有的知识、方法、经验积累中找到解决问题的源头。最后的统计数据中第(1)问的得分率达到了95%,第(2)问的得分率不到30%,可以看出第(2)问对学生的思维能力提出了挑战,这也恰恰是目前作图题的命题趋势。
(二)打破传统,考查素养
直尺是用来作直线,而圆规是用来作等长的线段,尺规作图就是通过作等长的线段来达成目的。而用无刻度直尺作图实际上是进一步约束条件:只用直尺作图,虽然失去了圆规的助力,却把尺规作图中的操作与思维结合起来,把几何直观和逻辑推理融合。用无刻度直尺作图是基于尺规作图,除了考查学生的动手操作能力,也需要学生在已有的知识、方法基础上,在自己思维的最近发展区,通过联想建构达到解决问题的目的。在整个解决问题的过程中,第(1)问考查了几何直观、空间观念、推理能力等核心素养,第(2)问更是全面考查了数学核心素养。
(三)升华题型,凸显本质
第(1)问到第(2)问是从常规的几何证明题到用无刻度直尺作图,也要求学生从明确解题目标到明确解题方向过渡。传统的尺规作图往往明确要求只需用一种或多种基本作图就可以作出图形。而用无刻度直尺作图,需要学生根据题中已知信息结合图形的几何特征来确定两个点或一个点(另一个点已知),再利用“两点确定一条直线”这一基本事实用直尺画出图形。虽说平时的教学中不要求学生写出作图过程,但学生只有对作图原理了然于心,才能顺利解决问题。因此在教学中,教师除了要教会学生如何尺规作图,还要教会学生论证为什么这样尺规作图。这样学生才会灵活运用所学知识和原理,提升思维能力,才能深入思考,促进深度学习。
三、思路分析及解法
如图3,方格中角的两边上有P1、P2、P3、P4、P5、O 和Q 这7 个格点,特别是点Q 是方格中OF 边上唯一的格点,利用直角三角形可知OQ 和OP1的长度都是5 个单位长度。第(2)问用无刻度直尺作角平分线,在点O 的基础上需要再找到一个到点Q 和点P1距离相等的格点就可以了。但如何从表格中众多的格点找到适合条件的格点呢?
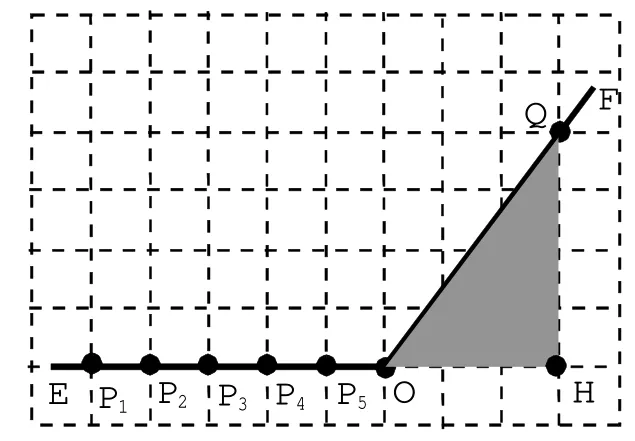
图3
不妨先动手画出角平分线的草图(铅笔画出),以缩小探究的范围,结合得到的条件OQ=OP1,锁定目标格点,再结合已有的知识加以验证。有哪些与角平分线有关的知识或方法呢?追本溯源,可知:①利用尺规作图中作一个已知角的角平分线的依据:构造三角形全等;②等腰三角形“三线合一”的性质;③菱形的对角线性质;④等腰三角形和平行四边形的组合可以得到角平分线;等等。
基于以上的分析,第(2)问生成了多种解法。
解法1:考虑到OQ=OP1且OP1是水平的线段,取水平线段CQ=OP1,如图4,用无刻度直尺作出射线OC即可。这里利用CQ=OQ 且CQ//OP1得到∠QCO=∠QOC,∠QCO=∠COP1,从而∠QOC=∠COP1,即射线OC 为∠EOF 的角平分线。也可以如图构造菱形OQCP1,根据菱形对角线的性质也可以得到射线OC 为∠EOF 的角平分线。
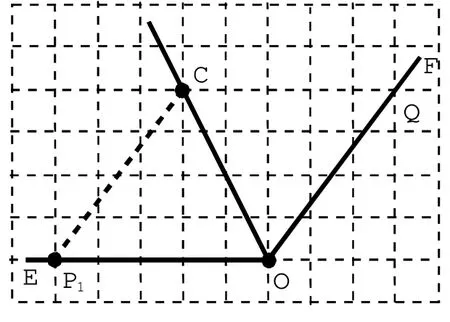
图4
解法2:考虑到OQ=OP1,可知△OQP1为等腰三角形,利用等腰三角形“三线合一”找出底边的中点即可得到顶角的角平分线。利用格子中的平行线和相等线段可以构造平行四边形,也可以通过平行线构造相似找到QP1的中点。
利用相似,构造基本图形和I 是线段QH 的中点得到线段QP1的中点D。射线OD 即为∠EOF 的角平分线。
解法3:利用格子中水平竖直的线段构造全等的三角形,得到∠EOF 的角平分线。
四、教学思考
(一)注重教材,夯实基础,掌握基本技能
作为教学和学习的第一手材料,教材应引起教师和学生的高度重视。尺规作图作为中考常考的题型,年年中考试题虽各不相同,但考查的主要内容基本一致。除了要求掌握的五种基本作图外,教材在部分几何内容中也有涉及尺规作图,如三角形全等判定中的探究活动,求作等腰三角形,作一些特殊的正多边形等,教学中教师可以加以利用,也可作适当拓展,如用尺规作图作出等边三角形、平行四边形,过圆外一点作出圆的两条切线等,这样既可以使学生熟练掌握基本技能,又可以提高学生学习数学的兴趣。
(二)回归知识,追本溯源,发展综合能力
对于尺规作图问题,教师在教学过程中不仅要教学生怎么尺规作图,还要剖析尺规作图的原理,明白为什么这样作。“点”是构成几何图形的最基本元素,尺规作图是通过“确定点”来实现的,因此解答尺规作图题需根据题意分析确定的点应满足怎样的条件,并运用尺规作图的本质——作等长的线段确定相应的点,而用无刻度直尺作图就是用来画直线、射线、线段的。教师在教学过程中要引导学生构建知识体系,归纳总结解决问题的知识或方法源头,如本题中可以归纳总结和角平分线有关的知识或方法:①构造全等三角形得到相等的角也包括角平分线的判定定理;②菱形的对角线平分每一组对角;③等腰三角形“三线合一”;④等腰三角形和平行线的组合可得到相等的角;等等。明白了问题的本质,探寻到解决问题的知识源头,形成解决问题的方法,这就是培养学生解决问题的综合应用能力。
(三)逆推综合,固本开新,促进深度学习
近几年中考的尺规作图题灵活多变,不再直白要求作什么,往往需要综合分析题意才明白需要怎么作出图形。本题用无刻度直尺作角平分线,就需要认真分析。第一步,根据题目观察特殊的格点特别是角的两边上的格点,如点Q,从而关注线段OQ=OP1;第二步,可以用铅笔直接画出角平分线的草图,结合OQ=OP1分析在假设的角平分线上的格点如何通过无刻度直尺画出,结合几何图形的性质得到该格点就是角平分线上的点;第三步,用直尺画出需要的直线或线段并加以验证。其中第二步需要学生在假设的角平分线上先锁定目标格点,再综合已有的知识和方法,结合已知条件,找到目标格点符合条件的作法,这就是逆向推理,然后再理顺思路,从条件出发,作出符合条件的图形。这是在数学解题中常用的方法。分析后再综合,从结论到条件,再从条件到结论,这对学生的思维能力提出了更高的要求。教师在教学过程中就需要通过对所学内容或方法进行有机整合、整体设计,这样学生既能加深对知识的理解和体会,还能将所学知识和方法迁移和应用,从而促进深度学习。

