基于水舱结构的UUV平衡液位算法研究

董 逸，梁 镜，唐文政

（1. 中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443003；2. 清江创新中心，湖北 武汉 430076）

0 引言

水下无人航行器，简称 UUV，是一种结合智能航行控制技术、水下声呐探测技术、高精度导航技术以及浮力控制技术等的水下航行体。通过这些技术搭建的UUV可以在水下完成相应的任务。目前，在海洋资源勘探、水下救援和军事上都有着比较广泛的研究和应用[1]。

随着社会的进步，为了满足信息化市场多元化以及多变的作战需求，实现体量大、航程远、抗干扰性强的中大型水下无人航行器，水下无人航行器内水舱装配是必不可少的。水舱的作用是为了调节航行器本身的密度，控制航行器的姿态，实现航行器的上浮和下潜。目前对于水舱液位的调整主要运用在潜艇领域，即有人参与调节过程；而对于装配水舱的水下无人航行器，调整航行器平衡状态同样是通过人为观察航行器的姿态来调节水舱液位，以满足航行器在出航前达到近似于零浮力状态。在装配水舱的无人航行器领域内调节平衡液位仍常依据人为经验为主的方式进行，无法形成科学化的调整方法。

具体方法：1）航行器处于水中静止状态下，通过控制水舱总水量，使得航行器整体浸没在水下可见的深度范围。2）通过外部传感器观察深度变化，得出深度偏差大小和深度变化方向，根据操作经验发出控制水舱的总水量的指令。当深度不再变大或变小时，确定水舱的总水量。3）确定总水量后，观察航行器的姿态俯仰角，以俯仰角为0的标准，得出偏差大小和方向。根据航行器结构和操作经验，分别调节艏艉水舱的液位。

人为调节平衡液位对于精度的把控不足，调节时间也相对较长，并且对人员经验要求很高，普适性不足。

本文是为了寻找无人航行器在水下平衡姿态时所对应的平衡液位。航行器平衡姿态是满足航行器深度稳定、航行器姿态稳定的状态。航行器深度变化、航行器俯仰角变化是反应航行器平衡姿态的直接参数。航行器水舱水量变化又影响航行器深度变化、航行器俯仰角变化。故无人航行器的平衡姿态可以通过水舱水量进行调节控制。因此，探究航行器在静水面情况下，水舱液位总量变化和航行器深度变化、艏艉液位差变化和航行器俯仰角变化的关系，并提出基于装配水舱的水下无人航行器状态下，通过PID算法实现自动调整航行器的平衡液位的研究方法。最后，结合航行器的水舱结构，实现调整艏艉水舱液位达到航行器平衡姿态的流程方法。

1 原理分析

方法原理是基于“浮性定律”，任何物体在液体中都会受到浮力的作用，浮力的大小等于物体本身所排开液体的重量。当物体的重量大于浮力时它就会下沉；小于浮力时就会上浮；等于浮力时就会悬停在液体中，这 2个力大小相等，但方向正好相反。

航行器静水力，对于水面状态的航行器而言，由于并非所有质量浸没在水面以下，其受到的浮力与浸没在水中的航行器排水体积成正比；航行器注水过程中，航行器的重量增加，即航行器排水体积同比增大，当航行器整个浸没在水中时，并且航行器的浮力与航行器的重量保持平衡时，则停止注水。此时的航行器状态被称为平衡状态，此时的液位被称为平衡液位。

航行器静止在水中受水的浮力、阻力、自身重力3力平衡。根据流体力学经验公式，水中阻力和运动方向截面积、运动速度成正比[2]。

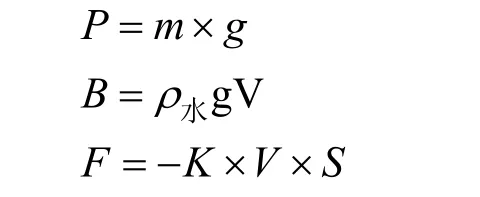
式中：m为航行器质量；P为航行器重力；V为航行器排水体积；B为航行器浮力；V为速度；S为截面积；K为系数。

该平衡状态是航行器的 P +B+F= 0的状态。

当满足 P +B+F= 0的状态后，结合航行器的结构，航行器姿态可能出现“低头”或者“抬头”的异常姿态，见图1航行器水下异常姿态图，即出现α＞0或者α＜0的情况（α正值为俯仰角向上）。

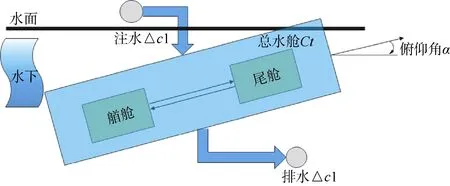
图1 航行器水下异常姿态图Fig.1 Abnormal underwater attitude of the UUV

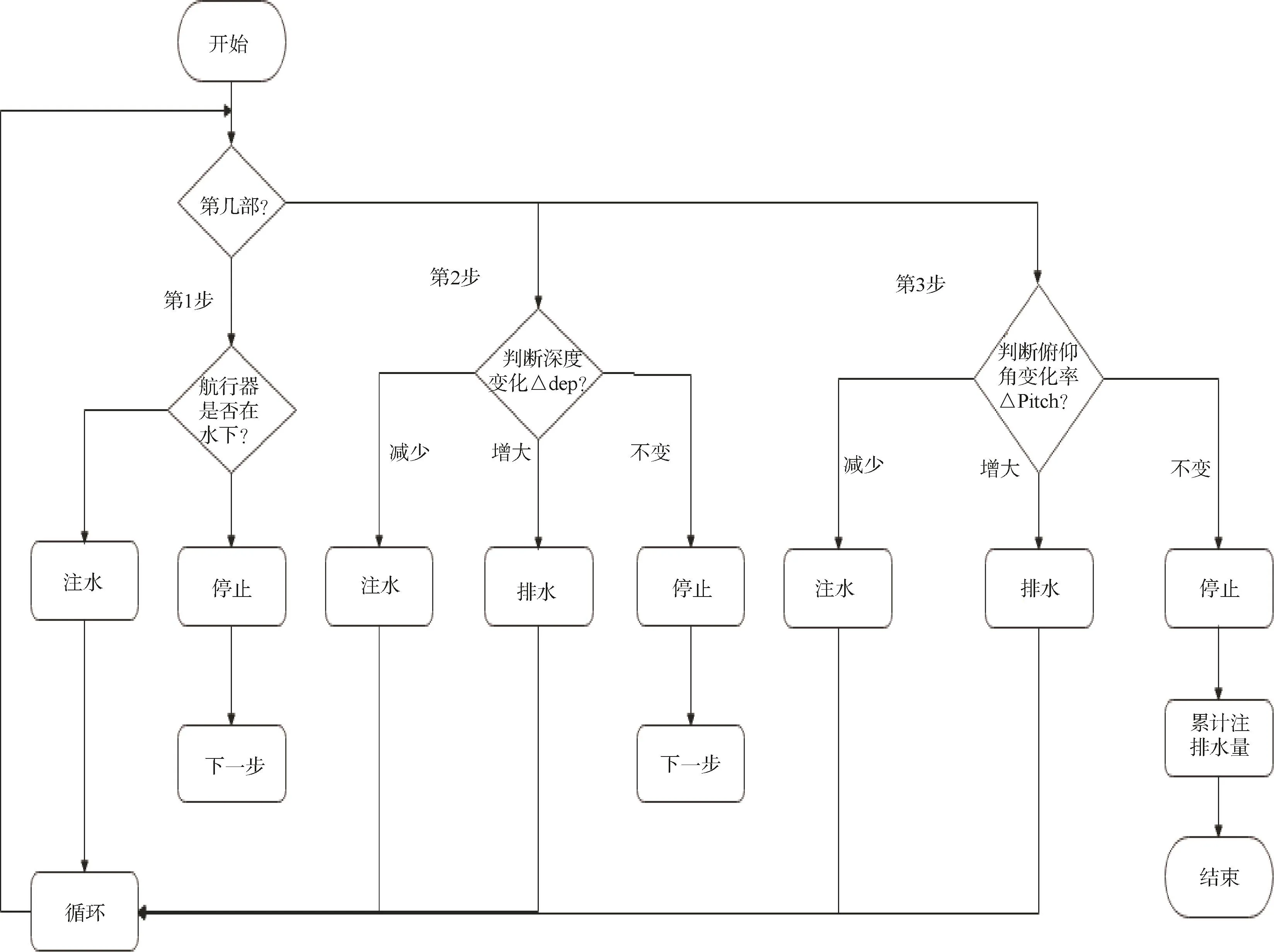
图 9 自主控制流程图Fig.9 Autonomous control flow chart

在保持总水量不变的情况下，通过调节艏艉舱水量的比例，控制航行器的姿态，使得当α=0时即达到水下平衡状态。

2 水下无人航行器模型

假设航行器在静水面，初始深度为0，初始俯仰角为0，初始液位为0，航行器因为浮力大于重力，处于水面状态。

2.1 数学模型

为了使航行器从水面到整个浸没至水下，通过调节水舱总水量，达到航行器深度变化的目的。在增加一个深度误差变化的扰动后，根据不断检测深度的变化，依据PID控制算法控制单位时间总液位变化量。对总液位变化量进行积分，可以得出液位总量。而通过液位总量与无人航行器的排水量的差与深度呈成一定关系，并通过深度变化反馈给输入，从而实现航行器总水量自动调整的系统模型，实现航行器悬停到水下效果，使其具有良好稳定性和动态性[3]。

其次，当航行器达到水下条件后，在增加一个俯仰角变化的扰动后，根据不断检测俯仰角的变化，依据PID控制算法对艏艉舱液位差变化量进行调整，对艏艉舱液位差变化量进行积分，可以得出艏艉舱液位差。通过艏艉舱液位差与俯仰角呈成一定关系，并通过俯仰角变化反馈给输入，实现对航行器姿态有效控制效果，使其具有良好动态性和鲁棒性。

2.2 确定过程的输入变量和输出变量

航行器深度误差为Δdep，即输入变量，是当前t时刻下的深度误差。Δc1为液位总量变化量（即输出变量），Δc1为正数时为注水状态；Δc1为负数时为排水状态；Δc1由1个开关控制[4]。

航行器俯仰角误差为ΔPitch，即输入变量，是当前t时刻下的俯仰角误差。艏艉液位差的变化量Δc2，即输出变量，艏艉液位差由艉舱液位减去艏舱液位。Δc2为正数时，艏艉液位差增大；Δc2为负数时，艏艉液位差减小；Δc2由2个开关控制，艏艉水舱分别由1个开关控制。通过航行器结构和液位总量，可以计算出艏艉舱的液位量。

2.3 系统方法

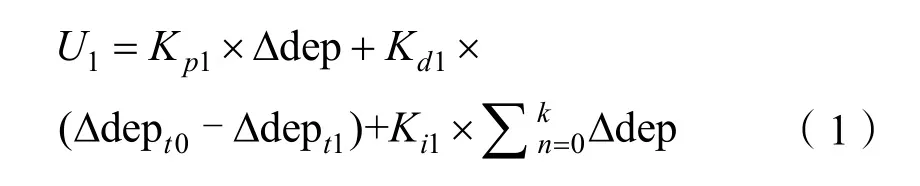
式中：U1为总液位量的变化量；Kp1为比例增益；Kd1为微分常数；Ki1为积分常数。

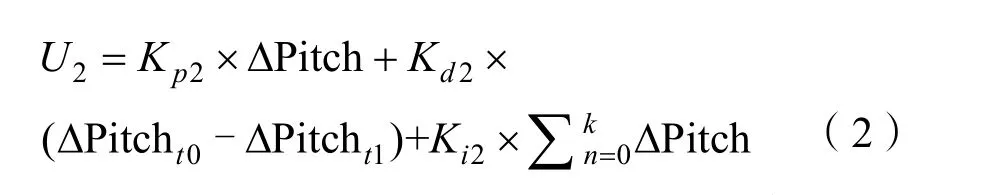
式中：U2为艏舱液位差的变化量；Kp2为比例增益；Kd2为微分常数；Ki2为积分常数。

3 PID控制算法设计

PID控制算法设计分为2步：寻找航行器水下悬浮的液位总水量；寻找航行器姿态稳定的艏艉水舱液位水量。

1）假设水中航行器静止在水面，水的阻力可以简化为深度的一阶导数，即纵向速度成线性关系，航行器在水面为正浮力状态。经过物理受力分析得：

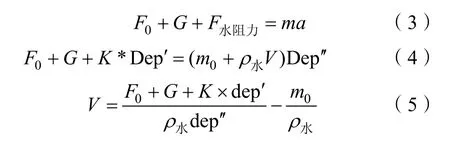
式中：K为系数；Dep为深度；Dep一阶导数为深度变化量；Dep二阶导数为深度变化量速度；F0为初始的正浮力；V为总液位量；m0为航行器在水舱的空时重量。

假设航行器在水面时增加某个深度误差的扰动，其深度误差Δdep的绝对值大于零，输入至PID算法控制器内，通过调节水舱总液位变化使航行器的深度变化为0和深度误差变化率为0[5]。并对总液位变化量进行积分，除去航行器本身的重力，通过传递函数（式（7））关系得出深度，并对深度变化率作为反馈输入系统，确定使航行器稳定在平衡状态艏艉液位总水量。

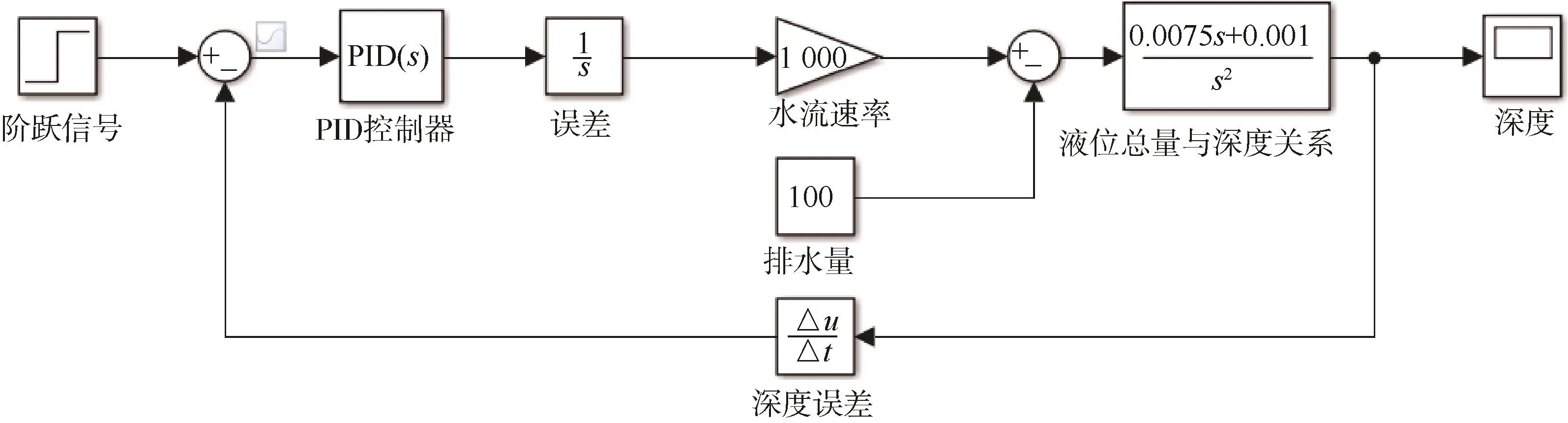
图2 航行器深度与水舱总液位调节模型图Fig.2 Adjustment model diagram of UUV depth and total water volume of water tank

2）假设考虑俯仰角在-90°～90°范围内进行变化，则俯仰角正切值与航行器艏段下降的距离成单调性。只考虑航行器艏段分析，原理同理公式3，经物理受力分析得：

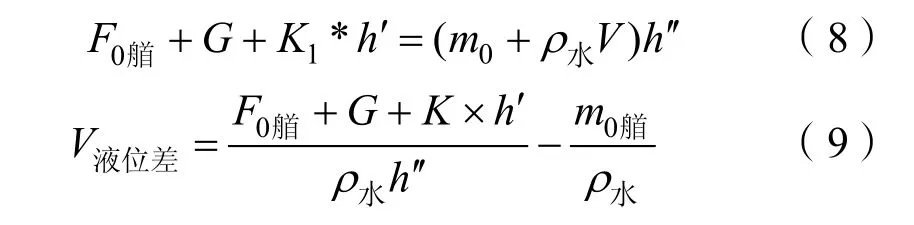
式中：K1为系数；h为航行器艏段与水平面垂直距离；h一阶导数为距离变化量，h二阶导数为距离变化量速度；F0艏为艏段的正浮力；V液位差为艏艉液位量差；m0艏为航行器在水舱的空时重量。

通过建模分析，信号输入为液位差，输入信号为I( t)=K2t；输出信号为俯仰角时，输出信号为所得传递函数同公式6。

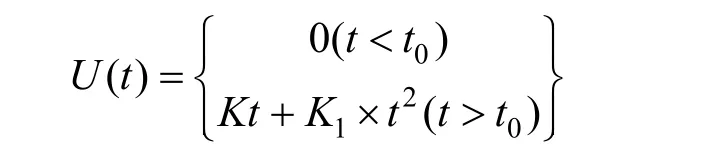
液位差与俯仰角正切值关系经计算其传递函数为

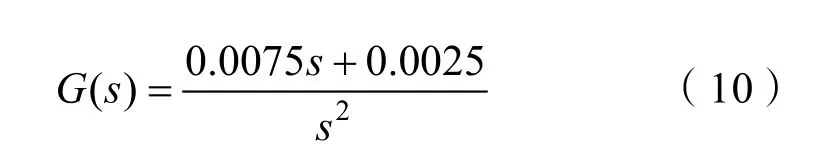
根据原理分析，假设航行器在水下，航行器调整目标为俯仰角0，给俯仰角某个扰动，俯仰角误差ΔPitch不为 0，将俯仰角误差输入至 PID算法控制器内，通过调节艏艉舱液位差的变化使得调整航行器姿态ΔPitch为0，并且ΔPitch变化率为0。对艏艉舱液位差的变化量进行积分，除去艏段本身的重力，通过传递函数（公式（10））关系得出俯仰角，并用俯仰角变化率作为反馈输入系统，最终得出航行器稳态下的艏艉舱液位差[6]。

结合第1步艏艉水舱液位的总液位量和第2步的艏艉水舱液位差得出各个艏艉舱液位。

图3 航行器俯仰角与艏艉水舱液位差调节模型Fig.3 Adjustment model of UUV pitch angle and the liquid level difference between bow and stern water tanks

4 仿真试验

为了验证本文 PID算法对航行器平衡液位的自主调整的有效性和可行性，运用上述建立的环境模型进行仿真试验。本文采用MATLAB进行仿真，仿真采用分步进行，第1步，对深度误差进行调节。其中仿真参数：初始深度误差设置为0.1 m，目标参数为0，水流密度设置为1 000 kg/m3，目标深度采用阶跃响应信号。当系统启动后一个深度变化扰动，默认该扰动即可出现0.1 m深度差，需航行器深度误差减少到0（即稳定到0.001 m范围内）。其目的是满足深度误差以及深度误差变化率均稳定为0。第2步，对俯仰角误差进行调节。其中仿真参数：初始俯仰角误差设置为0.1°，水流密度设置为1 000 kg/m3，俯仰角误差扰动采用阶跃信号响应，当给系统一个俯仰角变化扰动，表示航行器受到结构不对称导致的姿态不均衡，航行器俯仰角减少到0.001°内收敛即可。其目的是满足俯仰角、俯仰角速度均稳定为0。

4.1 深度误差调节

在执行第1步深度调节时，航行器处于静水面，由于浮力大于重力，航行器在开始注水液位调节时，深度无明显变化；当航行器的重力大于浮力时，航行器深度会出现变化，深度呈增大趋势，航行器纵向速度大于 0。此时航行器进行排水液位调节，减缓深度呈增大趋势，液位控制直到纵向速度小于 0，深度呈减小趋势。反复进行调节总液位直到纵向速度接近于 0，并使航行器整体浸没于水中。其中，液位调节总量基于算法计算得出。

PID 算法内设置 Kp为 0.075，Ki为 0，Kd为 0.1，N为 0.5[7]。不同的水下无人航行器对水舱配置不同，该参数也需要做相应调整。在满足深度误差低于0.000 2时调整完成。

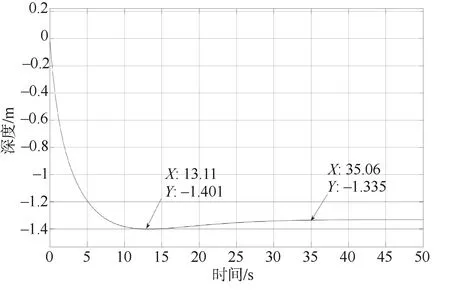
图4 深度值仿真曲线Fig.4 Simulation curve of depth value

深度最大超调1.4 m，超调量为1.977%，上升时间为4.7 s，在约35 s达到稳定在水下1.33 m。

通过深度误差变化量与液位总流量之间关系以及传递函数（公式（7））实现液位总流量与深度之间的转换[8]。本仿真验证过程中，在水下1.33 m时，水下最大水舱总液位为100 L。

图5 总液位变化仿真曲线Fig.5 Simulation curve of total liquid level change

该过程的液位总量上升时间为 8.1 s，水舱水量超调为107.6 L，并在35 s满足液位总流量100 L的要求。

当航行器开始调节液位时，由于需调节航行器正浮力，水舱液位需进行注水。13 s首次达到最大深度，深度变化率为0时，液位总量超过了平衡状态，航行器具有负浮力，航行器又会进行水舱液位排水。当深度变化率以及深度误差变化率为0时，在 35 s水舱液位停止调整，即而对深度值无需定量的要求。

4.2 俯仰角误差调节

在完成航行器深度调节后，由于航行器结构差异或者艏艉水舱液位调节不均衡导致航行器俯仰角不为0，因此需要第2步姿态调节过程。在保证总水量不变的前提下，航行器俯仰角出现大于 0时，即需要艏舱进行注水或者艉舱排水，减小艏艉液位差；航行器俯仰角出现小于0时，即需要艉舱进行注水或者艏舱排水，增大艏艉液位差。航行器俯仰角速度出现大于0时，即表示俯仰角呈增大趋势，需对液位调节量需要增加；俯仰角速度出现小于0时，即表示俯仰角呈减小趋势，需对液位调节量需要减少。直至航行器俯仰角为0，并且俯仰角速度也为0，则完成航行器姿态调整，记录当前艏艉液位作为平衡液位。

PID 算法内 Kp为 0.075，Ki为 0.025，Kd为 0.5，N为5[7]，在满足俯仰角速度低于0.000 2时为调整完成。

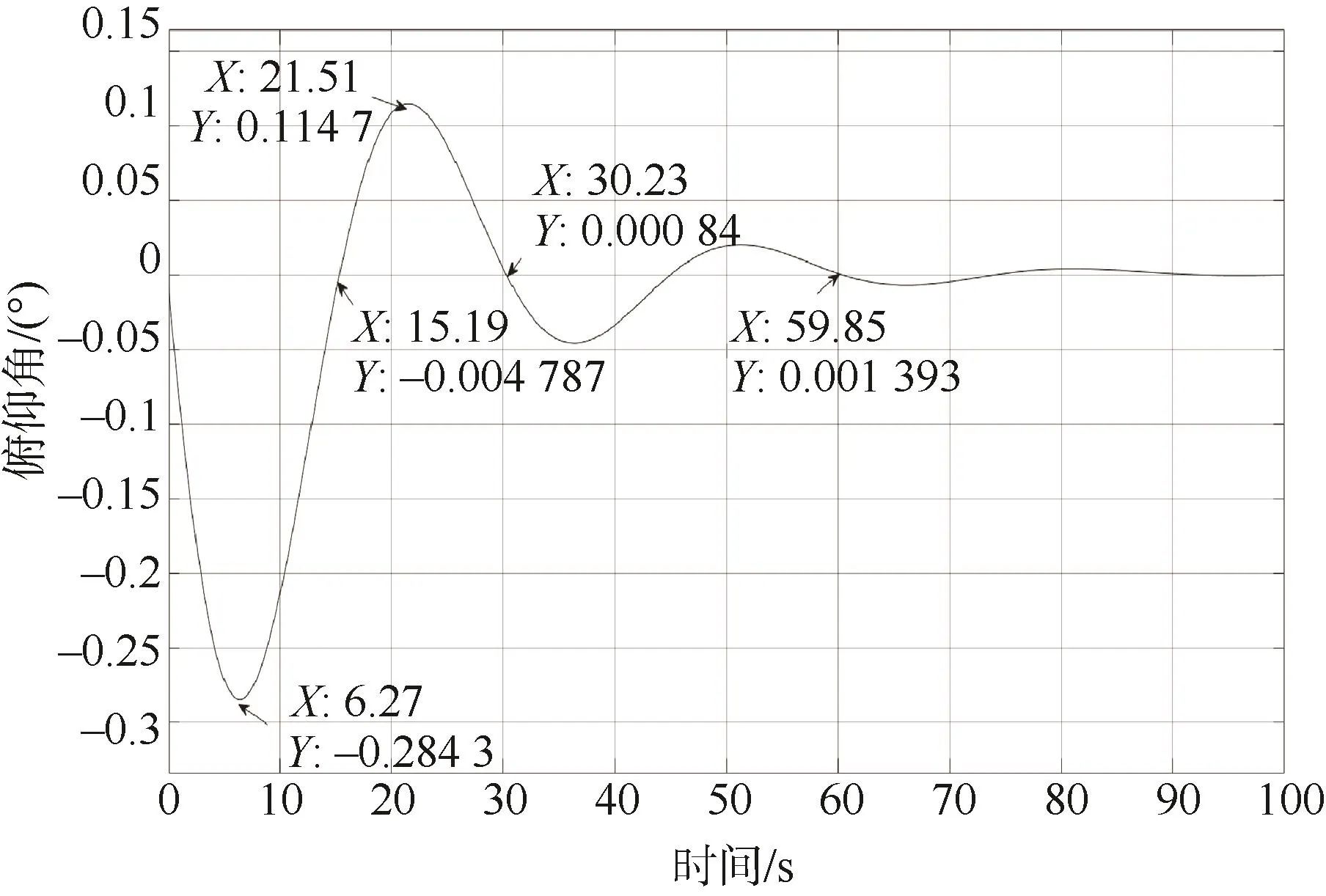
图6 俯仰角仿真曲线Fig.6 Simulation curve of pitch angle

图7 俯仰角速度仿真曲线Fig.7 Simulation curve of pitch angular velocity

俯仰角最大超调-0.28°，超调量为1.984%，调节目标是使俯仰角、俯仰角速度均为 0。在 6.27 s俯仰角速度第1次达到0，但由于此时仍存在调节水舱过程为最大水量，处于非平衡态，使得航行器艏舱为排水调节姿态。在21 s俯仰角速度第2次达到0，但由于俯仰角不为0，处于非平衡态，使得航行器艏舱为注水调节姿态；经过分析，在60 s时满足俯仰角、俯仰角速度均为0。

基于俯仰角误差变化量与艏舱液位总流量之间的关系，通过传递函数（公式（10））实现艏舱液位差与俯仰角的正切值的转换[8]。本仿真验证过程中，在水下俯仰角为0时，艏艉舱水舱液位差为50 L。

图8 艏艉水舱液位差仿真曲线Fig.8 Simulation curve of liquid level difference between bow and stern tanks

在8.09 s达到最大液位差53.94 L，并在60 s满足水舱液位差50 L的要求。

根据第1步结果，水舱和液位为100 L，水舱差液位49.8 L，可以推测艏舱液位25 L，尾舱液位为75 L。实际结果均在100 s内进行收敛，与实际设计的水下无人航行器仿真模型结果相同。

5 实现方式

自动调节过程，由仪器仪表代替人为的观察，并由航行器自主进行判断控制水舱的水量，模仿人为手动调节的过程。

自主过程控制实现方式是通过软件算法实现自主的调节过程。其中调节过程分为3步：1）通过对艏艉舱交替注水方式进行，每次注水量可以参照总水舱5%～8%，调节航行器至水下状态；2）通过深度变化情况，调节艏艉水舱总液位，采用对艏艉舱交替注排水方式进行，每次注水量可以参照总水舱2%～5%，使航行器稳定在水下，处于悬浮态；3）通过航行器姿态变化情况，调节艏艉水舱液位差，采用对艏艉舱交替注排水方式进行，每次注水量可以参照总水舱 0.5%～2%，使航行器以俯仰角为0的姿态稳定在水下。

6 结束语

在水下无人航行器自主调节平衡液位过程中，利用经典的PID算法实现平衡液位自主调节。该算法不仅具有稳定性好、适应性高、计算量小、容易实现等特点，同时便于在工程上进行应用。由算法仿真结果可知，水下无人航行器的PID平衡液位自主调整超调量小，能够在较短时间内稳定；水下无人航行器水舱平衡液位自主调整能较好地适应外来干扰，具有较强的鲁棒性和自适应性，可以获得很好的控制效果，具有较好的工程适用前景。