基于拓扑优化方法的舱体筋板设计

韩忠磊，鲁 鹏

（1. 中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443003；2. 清江创新中心，湖北 武汉 430076)

0 引言

水下设备的研制与发展对我国开发利用海洋资源、布局军事战略具有重要意义。耐压舱体是水下设备不可或缺的一部分，其足够的强度是设备在水下安全有序工作的前提，其轻量化是设备总体满足衡重参数的保证。一般的耐压舱体由筒壁和内部环肋构成，其几何参数可由行业标准或者企业标准里的经验公式确定或者验算，当加强筋板并非环肋时，设计参数的确定就只能凭设计师的经验完成，再进行仿真验证，这大幅增加了研发成本。

拓扑优化方法可以为结构设计提供很重要的指导。Michell[1]早在 1904年就提出了拓扑优化的解析方法，得到了最优Michell准则的桁架。后经过100多年的发展，拓扑优化的数值方法得到了广泛的应用。如隋允康[2-3]等将ICM拓扑优化方法应用于刚架结构，以结构重量为目标函数，研究了多工况下刚架结构在应力约束下的优化结果；范文杰[4]等采用基于实体各向同性材料罚函数的多目标拓扑优化方法，使得车架结构同时满足了静态刚度和低阶固有频率的要求；龙凯等[5]利用基于RAMP插值函数的ICM拓扑优化方法对主轴承盖结构进行了优化设计，实现了结构体积最小化；芮强等[6]基于拓扑优化技术的变密度方法对某动力舱支架结构进行了优化，改善了支架的静、动态力学特性；Tamijani[7]等采用Kriging插值模型和遗传算法对带肋板结构进行优化设计，大幅缩短了计算时间；张聪等[8]应用变密度拓扑优化方法，减轻了三体船横舱壁优化区域内50%的质量，实现了非水密舱壁结构的轻量化设计；朱鑫垚等[9]利用ABAQUS 软件对汽车活塞连杆进行了拓扑优化，减重的同时保证了加工工艺性。

本文采用变密度拓扑优化方法，以单元的相对密度作为设计变量，舱体柔度最小为目标，计算了耐压舱体外压状态下的载荷传递路径，并以此为依据设计了筋板，最后对优化模型进行了分析。

1 优化问题分析

耐压舱体模型如图1所示，系统主要由舱壁、隔舱板和2个盖板组成，为抵抗大深度水下压力，盖板被设计为球面形状。盖板与隔舱板之间形成的舱室可用于放置水下仪器设备等，该舱体与其他系统的机械及电器接口等特征在此处已被隐藏处理。

图1 耐压舱体模型Fig.1 Cabin model

考虑水下使用环境，该舱体选用了钛合金TC4材料，其力学性能如表1所示。如图2所示，通过有限元仿真计算，在指标要求的外压下，即使使用了较高强度的钛合金材料，该设计模型仍然被破坏掉了。最大应力为1 297 MPa，最大位移为10 mm。若只是简单地增加舱体壁厚，必然会大幅提高系统重量和成本。最大应力出现在舱体圆柱面与端面过渡的地方，配合位移云图分析可知，可在过渡处进行筋板加强，来提升整体强度和刚度。筋板的数量和布置形式可通过拓扑优化方法分析得出。

表1 TC4材料属性Table 1 TC4 material properties

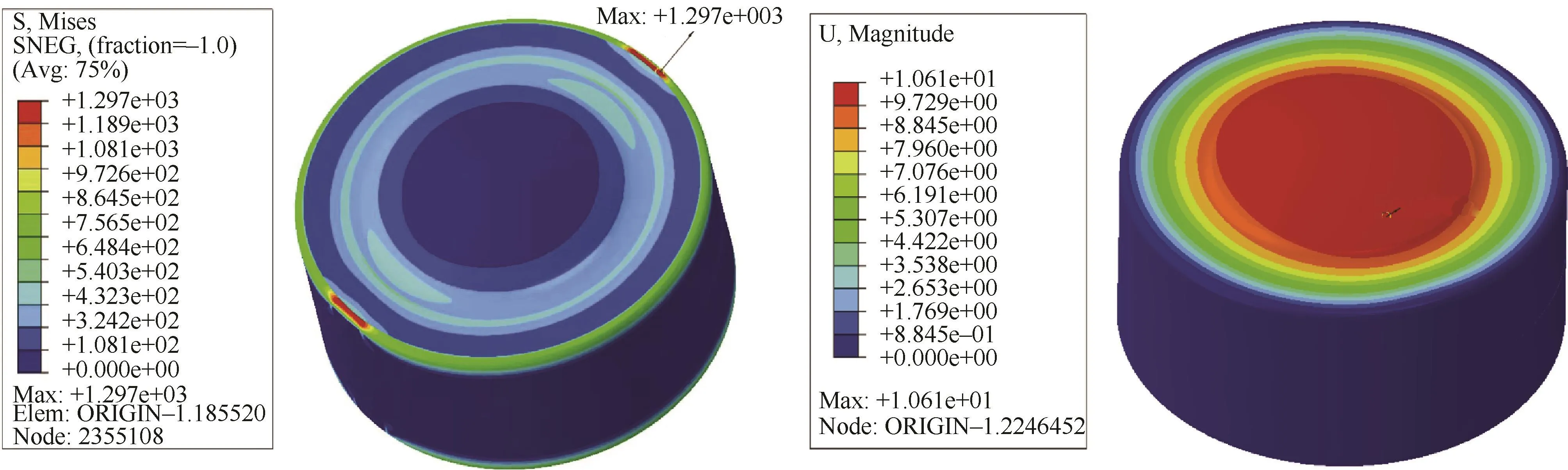
图2 无筋板舱体外压下应力（MPa）及位移（mm）云图Fig. 2 Cloud diagram of stress（MPa）and displacement（mm）under external pressure of cabin without stiffeners

2 舱体优化设计

2.1 拓扑优化数学模型

拓扑优化的基本思想是在给定载荷及边界条件的情况下，使得目标函数达到最优解，即将设计空间内的材料进行最优化的分布。与传统优化设计不同的是，拓扑优化只需给出结构参数（材料特性、载荷和边界条件）和材料去除体积比[10]。

本文的原始模型为无筋板的舱体，为在合适的位置添加筋板，需找到耐压舱体受外压作用下载荷的传递路径，即将问题转化为舱体材料分布状态的0～1优化。设计空间内有限单元的相对体积密度即为本文的设计变量，设计空间中材料密度接近于1或等于1（有材料）的部分即为筋板需要布局的地方。对于0～1组合优化问题，由于网格单元太多，难以计算。采用基于SIMP 材料插值模型的拓扑优化方法[11]，可以得到具有可变刚度的各向同性材料，即材料的相对体积密度x可在0～1之间连续变化。如式（1）所示，通过引入惩罚因子，使得设计变量x趋近于0或1，从而消除没有物理意义的中间密度，同时利用SIMP插值模型可方便构造灵敏度函数，为优化求解提供搜索方向，提高计算效率和得到最优解。

SIMP材料插值模型如下式：

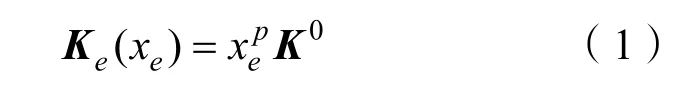
式中：Ke为第e个单元优化后的刚度矩阵；0K为第e个单元初始刚度矩阵；xe为第e个单元的相对密度；p为中间密度惩罚因子，取p为3。xe的取值区间为[0，1]，当xe取1时，表示该单元充满材料。为了避免刚度矩阵的奇异性，通常将单元密度取一个下限值，即xmin，一般取值较小。

本文以耐压舱体的刚度最大即柔度最小为优化目标，以单元相对密度xe作为设计变量，以体积分数作为约束条件，建立了拓扑优化数学模型。

式中： x为单元的相对密度向量；C为结构总体柔度，用应变能来表示；F为结构载荷向量；U为结构位移向量；K为结构总体刚度矩阵；V为结构优化后的体积；f为保留体积比；V0为结构设计域体积；ve为第e个单元的体积；xmin为单元密度下限取为0.001；xmax为单元的密度上限。根据式（1）-（2）的理论，便可在 Abaqus中对耐压舱体进行拓扑优化。

2.2 优化结果及筋板布置

有限元分析软件Abaqus里面的拓扑优化模块支持2种算法：通用算法即变密度法和基于条件的算法，前者更灵活，适用于大多数问题，后者效率更高，但能力有限。默认情况下，优化模块使用通用算法。利用该模块进行拓扑优化的流程为：导入简化的几何模型，定义材料属性，对模型进行网格划分，施加载荷和约束，定义拓扑优化参数，提交优化任务，计算求解。

本文优化模型为中心对称结构，为提高计算效率，仅选取1/4模型进行计算。在Abaqus中划分的网格如图3所示，浅绿色区域为设计空间，红色区域是固定约束（考虑舱体安装至平台的机械接口），舱体外表面承受均布载荷即外压。优化设计空间为舱壁部分，以其结构刚度最大即柔度最小化为优化目标，以单元相对密度作为设计变量，以体积分数0.4作为约束条件。优化结果如图4所示。

图3 1/4舱体模型网格划分Fig.3 1 / 4 cabin grid model

图4显示了经过优化之后，余下单元的单元相对密度分布情况。红色部分表示相对密度为1或者接近1，图中镂空区域为需要删除材料的地方，相对密度接近于0，图4很清楚地展示了舱体受外压时力的传递路径。根据图4的结果，可设计筋板的布置。圆周等距离布置14个筋板，在隔舱板上下层对称布置，如图5所示。

图4 拓扑优化结果Fig.4 Topology optimization results

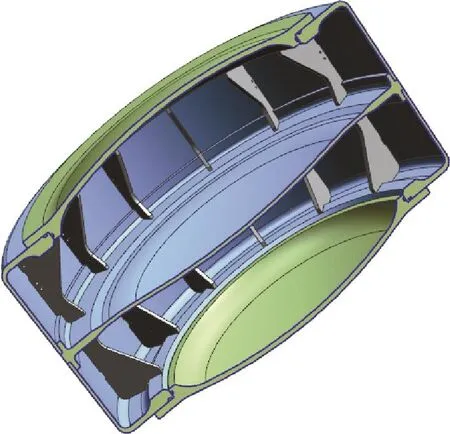
图5 带筋板舱体模型Fig.5 Cabin model with stiffeners

2.3 设计结果分析

对优化筋板布置的舱体模型重新进行静力学分析，结果如图6-7所示。带筋板耐压舱体在外压下的Mises应力云图如图6所示，最大压力在筋板边缘弯折处，最大应力为779 MPa，小于其材料的屈服应力（825 MPa）。带筋板耐压舱体的位移云图如图7所示，最大位移位于盖板中心，最大变形量为3.228 mm，变形量仅为之前的1/3，满足使用要求。

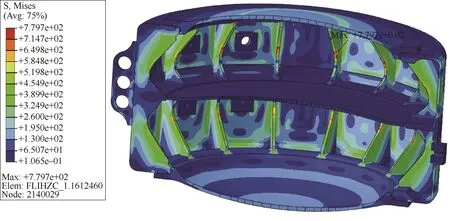
图6 带筋板舱体的Mises应力云图（MPa）Fig.6 Mises stress nephogram of cabin with stiffeners（MPa）

图7 带筋板舱体的位移云图（mm）Fig.7 Displacement cloud diagram of cabin with stiffeners（mm）

3 结束语

水下舱体作为耐压部件，承载内部设备，承受外部压力，强度至关重要。本文通过有限元软件对舱体筋板进行了优化设计，结论如下。

1）采用基于 SIMP插值的变密度拓扑优化方法，求解了耐压舱体在外压作用下的传力路径，并以此为依据优化了舱壁上加强筋的布置。

2）优化后的舱体模型最大应力减小到了材料的许用范围内，并且变形量大幅减小。说明该拓扑优化方法对筋板设计具有一定的指导意义。