超声波无损探伤仿真实验设计

段 茜，廖思岚，周泰言，向廷伟，王毅豪，何晋宇

（西南石油大学 理学院，四川 成都 610500）

超声波无损检测技术因其检测灵敏度较高，对测试介质或试验人员无损，测试方法简便且成本低廉，已被广泛应用于工业、医学和地质学等领域。例如，人们采用声波透射法开展桩基质量检测[1]；利用超声波时域和频域特性研究粘结混凝土结构[2]；开展岩石室内超声波透射实验和岩石力学实验的同步测试，利用岩石声学参数来预测其物理力学参数[3]；利用超声波的成像特征来检查胎儿的健康状况以及身体器官或骨骼肌肉是否存在损伤[4]等。

本文简单介绍了脉冲反射法超声波无损探伤原理，并基于二阶声波波动方程，采用有限差分法对超声波无损探伤实验进行数值仿真，仿真程序界面简洁，操作步骤简单，对声波波场在固体介质中的传播过程进行了二维动画展示，使学生可以形象观测到声波遇到缺陷阻挡后的反射、折射和绕射过程。通过计算无损模型中的波速，评价了该方法的计算精度。学生通过计算不同裂缝长度和宽度下的声波衰减系数，从而理解裂缝参数对声波衰减系数的影响，结果也为介质中裂缝参数的声学检测提供了理论依据。

1 超声波无损探伤原理

除了穿透法和双晶头脉冲反射法，脉冲反射法也是目前超声探伤的主要方法。本文对脉冲反射法超声波无损探伤实验开展研究，该方法的原理是将发射探头和接收探头置于介质的同一个端面上，当脉冲发生器产生的高压电信号加在发射探头上时，探头受到激发，产生一个瞬态的振动，该振动以一定的速度在介质中传播。当介质为无损介质时，脉冲振动到达样品的另一端面时被反射，反射波被接收探头接收，此时接收端波形只有初始波和底面反射波。当介质中存在缺陷时，脉冲振动遇到异质界面会发生发射，接收端波形在初始波和底面反射波之间会出现缺陷回波，缺陷回波的位置取决于声波在介质中遇到异质界面时传播的路程，缺陷离发射和接收探头越远，缺陷回波传播的路程越长，据此可以确定缺陷在介质中的位置。缺陷回波的振幅取决于缺陷的几何形态，如缺陷呈水平分布，其长度越长，阻挡声波传播的反射面积也越大，缺陷回波的振幅越大。

2 虚拟仿真实验设计

基于声波波动方程，对含缺陷介质的声波波场进行有限差分数值模拟，波场快照图以二维动画方式显示，仿真界面如图1 所示。设介质的尺寸为50 mm（长度）×50 mm（直径），采样的时间步长为10 ns，空间步长为0.2 mm，探头位于点（25 mm，0 mm）处，左右边界采用吸收边界条件[5]，上下边界采用反射边界条件。振源子波函数采用雷克子波[6]，主频为100 kHz。

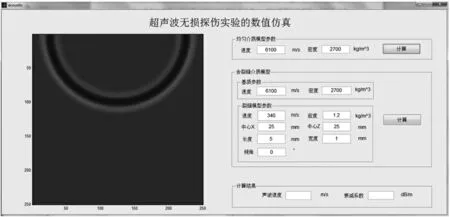
图1 超声波无损探伤实验的数值仿真界面

2.1 无损模型中波速的计算

设介质中无缺陷，介质中的声波速度为6 200 m/s，以探头的激发信号为振源，模拟其通过无损模型后探头接收的波形图，再拾取底波波形的初至来得到波的传播时间，利用公式（1）即可计算出声波速度Vp。

式中，L为介质长度，△Τp为底波在介质中的传播时间。介质在8 μs、10 μs 和12 μs 时的声波波场快照分别如图2（a）至图2（c）所示，其中▲代表探头位置，探头发射和接收的波形如图3 所示。从归一化振幅波形图上提取底面反射波的波至时间，为16.06 μs，由公式（1）可计算得到声波速度为6 226.7 m/s，与预设速度值6 200 m/s 相比，相对误差仅为0.43%，说明该数值模拟方法具有很高的精度。

图2 无损模型声波位移波场快照图

2.2 缺陷位置的检测

假定距发射信号位置x处有一裂纹，并设从激发到接收裂纹回波信号的时间间隔为t，波速为Vp，则由

式（2）可判断裂纹所在的具体位置。

设介质中的声波速度为6 200 m/s，缺陷为气孔，位于模型中心，缺陷半径为0.6 mm，缺陷中的声波速度为340 m/s，介质在8 μs 时的声波波场快照如图4 所示，接收端的波形图如图5 所示。从归一化接收端的波形图提取缺陷波的波至时间，为8.35 μs，由公式（2）可计算得到缺陷位置在距探头0.024 1 m 处，与预设模型缺陷距探头的位置0.024 4 m 相比，相对误差为1.23%。

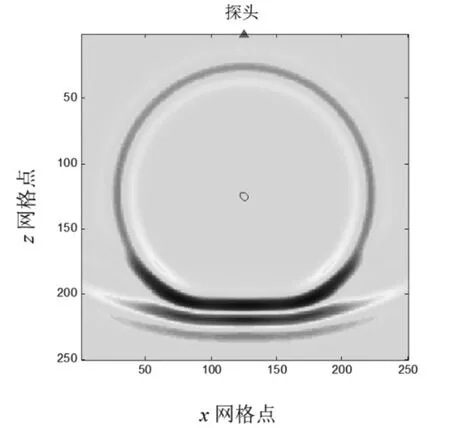
图4 缺陷模型声波位移波场快照图

图5 缺陷模型接收端波形图

2.3 单裂缝损伤程度的检测

采用信号对比法，测量探头发射声波信号的幅度A0，再记录缺陷回波的声波幅度A，即可利用公式（3）计算出介质的声波衰减系数。

式中，x为缺陷距发射信号位置。

2.3.1 裂缝伸长度对声波衰减系数的影响

设介质中心有一单裂缝缺陷，裂缝宽度为2 mm，裂缝长度分别为2 mm，4 mm，6 mm，8 mm 和10 mm。介质中的声波速度为6 200 m/s，缺陷中的声波速度为340 m/s，裂缝长度为2 mm，6 mm 和10 mm 的介质在8 μs 时的声波波场快照分别如图6（a）至图6（c）所示，相应的接收端波形图分别如图7（a）至图7（c）所示。从归一化波形图上提取激励信号的幅度和缺陷波的声波幅度，利用公式（3）即可计算出介质的声波衰减系数。绘制声波衰减系数与裂缝长度的关系曲线，如图8 所示，可以看出，随着裂缝伸长度的增加，缺陷波反射的能量增加，幅值增大，声波衰减系数减小。

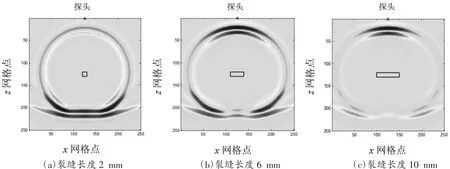
图6 单裂缝模型声波位移波场快照图

图7 单裂缝模型接收端波形图

图8 声波衰减系数随裂缝长度变化

2.3.2 裂缝张开度对声波衰减系数的影响

设介质中心有一单裂缝缺陷，裂缝长度为10 mm，裂缝宽度分别为2 mm，4 mm，6 mm，8 mm 和10 mm。介质中的声波速度为6 200 m/s，缺陷中的声波速度为340 m/s，裂缝宽度为2 mm，6 mm 和10 mm 的介质在8 μs 时的声波波场快照分别如图9（a）至图9（c）所示，相应的接收端波形分别如图10（a）至图10（c）所示。绘制声波衰减系数与裂缝宽度的关系曲线，如图11 所示，可以看出，随着裂缝张开度的增加，缺陷波反射的能量相差不大，声波衰减系数几乎不变，裂缝张开度对声波衰减系数几乎不产生影响。

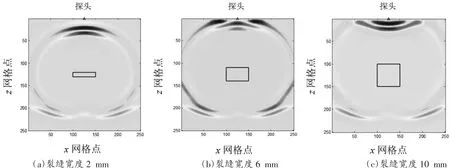
图9 单裂缝模型声波位移波场快照图

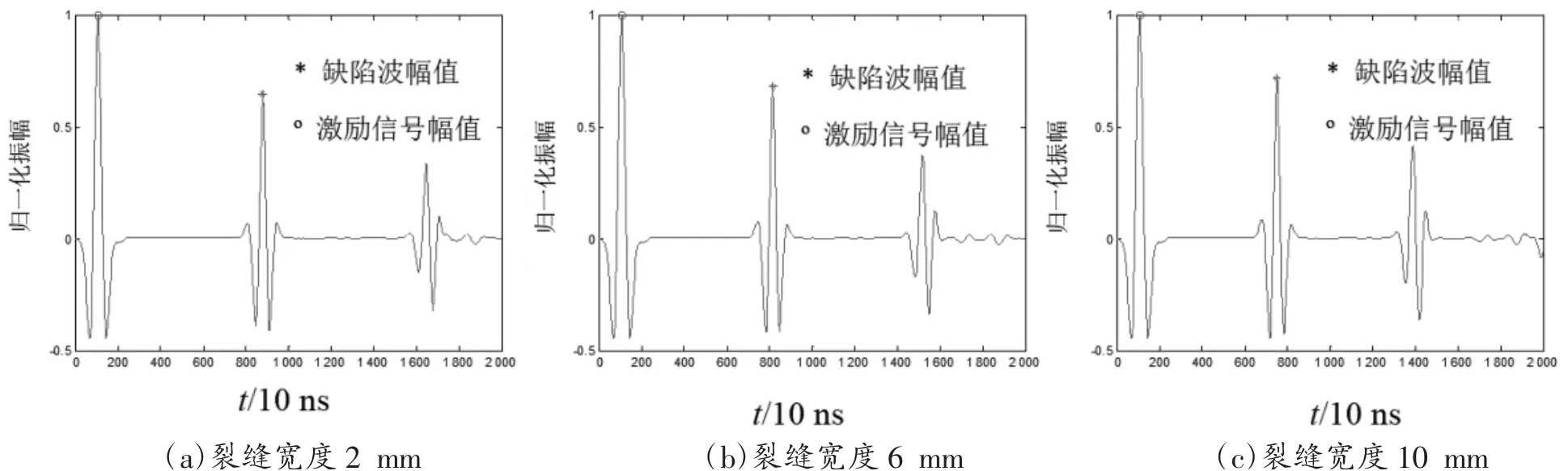
图10 单裂缝模型接收端波形图

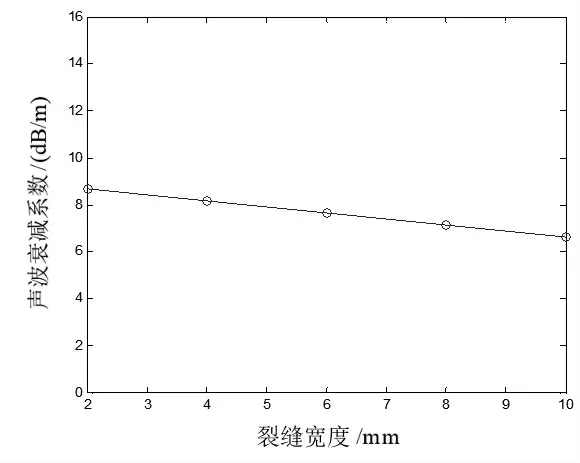
图11 声波衰减系数随裂缝宽度变化

3 结束语

基于声波波动方程，对超声波无损探伤实验进行了数值仿真，仿真程序界面简洁，操作简便且计算精度高，抽象的声波波场传播过程以动画的形式得到了直观展示，学生可以通过自主设计裂缝缺陷的位置、长度和宽度等信息，从接收端波形图中提取不同裂缝参数下的缺陷回波的波至时间和振幅，分析裂缝参数对声波衰减系数的影响，促进了学生对无损探伤原理的深入理解，提高了教学效果。