基于人工智能的六子棋博弈平台研究与实现

段 浴，王宛宛

（1.重庆移通学院 大数据与软件学院，重庆 401520；2.重庆交通职业学院 大数据学院，重庆 402247）

人工智能不断发展，在围棋、五子棋、象棋等棋类当中的应用非常广泛，众所周知的有AlphaGo、深蓝等[1-2]。五子棋人尽皆知，然而六子棋知道的人却很少。相比于五子棋、象棋、国际象棋等其他许多棋种，六子棋不具先手优势[3]。而且理论上游戏所使用的棋盘可以是无限大的。事实上，六子棋的状态空间复杂度和游戏树复杂度远比五子棋高几个数量级，其已经和围棋及国际象棋的复杂度差不多[4]。本系统就是为人工智能应用于六子棋做铺垫，为机器人与玩家对弈做铺垫。本系统会为玩家提供博弈平台，并做出研判。

1 系统需求分析

本系统主要是做六子棋博弈研判。棋局中先完成连六或长连者获胜。当所有棋盘交点全部下满而无人宣告获胜时为和局。

1.1 系统功能性需求

（1）悔棋，对弈过程中，可进行悔棋操作。

（2）判定是否获胜。玩家每次落子后，系统会搜索当前棋面，并进行判定，直至某方获胜。

（3）重新开始，在对局过程中如有一方提前认输或者已分出胜负。便可开启下一局对弈。

1.2 系统功能性需求

（1）先手控制，走子提示。

（2）计时器，通过系统计时器来提示玩家，限制玩家每一手棋的时间。

（3）角色控制，当轮到对方下棋时，己方角色会变成灰色，且不能移动棋子。

2 系统设计

2.1 系统总设计

（1）在界面方面：应简单实用方便，可以满足不同层次使用者的需求。

（2）在实现方面：对六子棋的数据结构、棋子触发、搜索算法等进行了设计和实现的过程。

（3）在系统规范方面：实现了程序的标准化、统一化，增强了软件的可扩展性、可维护性以及实用性。

2.2 软件结构

整个软件分为两个主要模块，第一个模块是界面部分，第二个模块是算法模块，主要是进行胜负判定的算法代码。

2.2.1 模块一

模块一主要是完成界面的显示以及与用户的交互、相关信息的显示以及与用户的交互、提示框等。该模块首先完成的是棋盘的显示，包括背景部分以及棋盘上的方格。另外一部分是菜单项，包含重新开始、后退两个操作。此模块包含的类有class MyFrame，class mypoint，class myline，还包括一些相应的监听类来响应用户的鼠标操作等。

2.2.2 模块二

模块二主要是完成对胜负的判定，是依照六子棋的规则来进行设计，在每一方落子结束之后判断是不是有一方已经能够连成六子，也就是胜出了。

此模块包含的类有class sixp、class search 等。

2.3 设计原理

软件的设计是依据吴毅成教授发明的六子棋的游戏规则来设计，这主要体现在算法模块上[5]。胜负的判断使用方法hadsix（），从各个方向扫描是否有连成六个子。

博弈判定的过程可分为两个部分。第一个部分为当对手落子后，AI 更新博弈树和主路径[6]。第二个部分为当自己落子后，AI 更新博弈树和主路径。AI 通过博弈树和主路径来记录博弈的过程，因此更新博弈树和主路径是等价的。

2.4 系统功能设计

重新开始菜单项可以以当前选择的模式重新开始；后退菜单项可以用来完成悔棋，使用户退回到上一步，可以连续使用，直到回到初始状态。

2.5 系统流程图

系统流程图如图1 所示。本系统使用二维数组储存棋盘信息，分别用0、1、2 表示黑子、白子、空白。每次落子后都会生成棋形向量，使用搜索算法对当前棋局进行博弈判定。

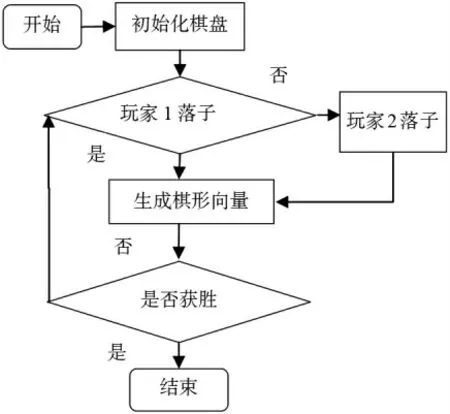
图1 系统流程图

3 系统实现

3.1 开发平台和工具选择

开发工具：Visual Studio 2017，开发语言：c#。

3.2 算法设计（UCT 算法）

3.2.1 UCT 算法简介

UCT（上限置信区间）算法，将蒙特卡洛树搜索与UCB 公式结合，基于UCT 的一些变形，是一种博弈树搜索算法[7-8]。与传统的搜索算法相比，它在超大型博弈树的搜索过程中具有时间和空间上的优势。

（1）selection（选择）：从根节点出发，使用UCB 公式，连续子节点向下至叶子节点进行选择。

（2）expansion（扩展）：在游戏结束前，创建一个或多个子节点，并选取其中一个节点。

（3）simulation（模拟）：从选定的子节点开始，用随机策略进行游戏。

（4）backPropagation（传播）：使用随机游戏的结果，更新从选择子节点至根节点。

3.2.2 UCT 算法过程

首先，以当前棋盘状态对应的节点，作为博弈树的根节点。每次UCT 搜索，是当前所到的节点，并不是尚未完全扩展的节点。如果该节点完全扩展，那么就计算UCB 值，选择最大的节点往下走[9]。最终可能出现两种可能：遇到了未完全扩展的节点，或遇到了终局节点。

终局节点就是直接沿着我们刚才来的路径，一个一个节点备份棋局结果，否则就以一个可行状态出发，进行随机模拟。该模拟过程就是随机在可行位置下不断下子，直到棋盘结束。该随机过程中并不记录任何东西。模拟的结果是从刚才生成的0/0 节点开始，依次向上备份结果。

抽象地说，就是在找当前UCT 树的主路径，然后取得主路径新生成的尾节点，从这个尾节点出发进行模拟，备份得分的对象是新的主路径，即为单次的UCT搜索。一次完整的UCT 算法求解，是要在限定的时间内进行多次UCT 搜索的。每次UCT 搜索，都会改变博弈树的结构，影响下一次UCT 搜索的主路径走向。而搜索得越多，结果也就越准确。

UCT 算法的执行位置介于record_part1 和record_part2 之间。因此，总算法的执行顺序为record_part1→ UCT → record_part2。若i 胜利，则mark=1；若i 失败，则mark=-1；若平局，则mark=0。伪代码如下：

4 系统测试

本系统采用黑盒测试方法。

4.1 功能测试

功能测试如图2 所示。

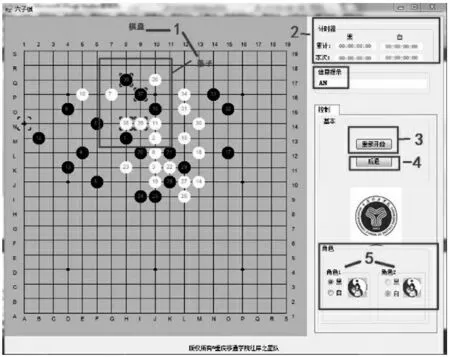
图2 功能测试

（1）棋盘|落子：在棋盘按先后顺序落子，六子棋的规则是黑色方先落一子，然后从白色方开始后各落子，直至获胜或棋盘走满。

（2）计时器：显示棋手双方一共用时和单次落子时间。

（3）重新开始：清空棋盘，重新开始游戏。

（4）后退：即悔棋，倒退回上一步。

（5）角色：显示棋手双方的信息。

胜负终局棋判定如图3 所示。

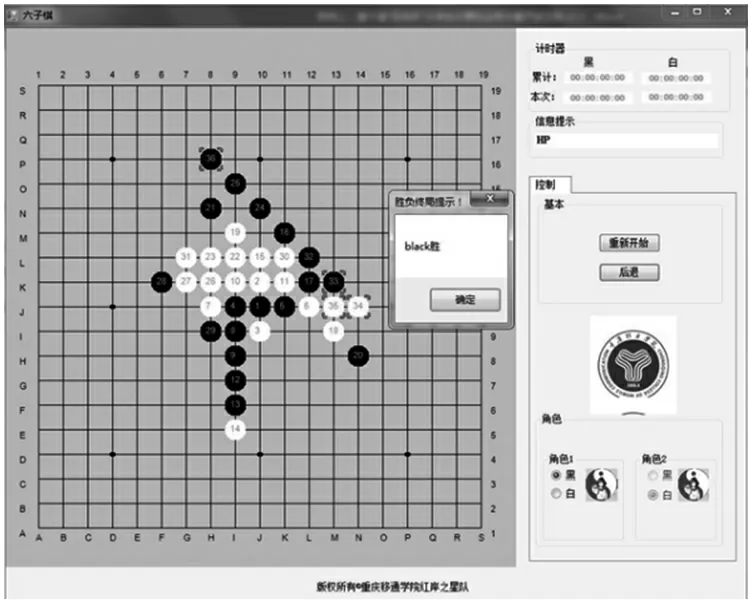
图3 获胜局展示

4.2 性能分析

测试方案是，邀请了5 组六子棋爱好者玩家使用本系统进行对弈，采用五局三胜制。使用比赛过程中每一个棋局的准确率指标来衡量系统的整体性能。

5 组分别为A、B、C、D、E 组，甲乙双方进行对弈，每完成一局便互换黑白执棋方。表1 至表5 分别为5组对弈情况表，表6 为5 组对弈情况汇总表。经统计，所有5 组对弈准确率均为100%，本系统达到预期设计效果。

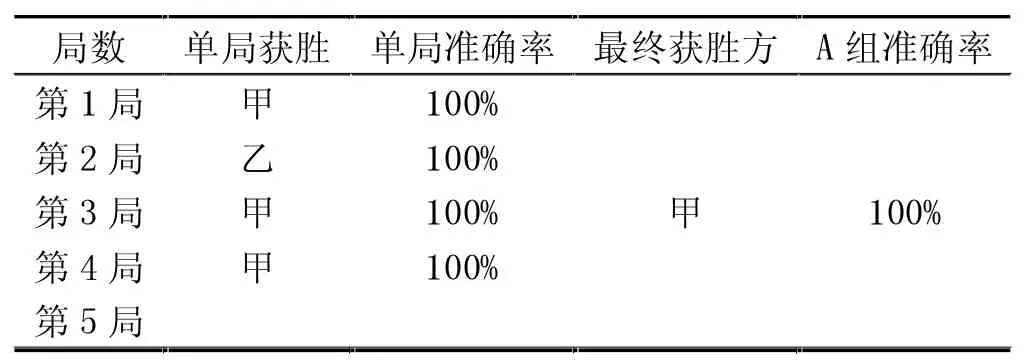
表1 A 组对弈情况表

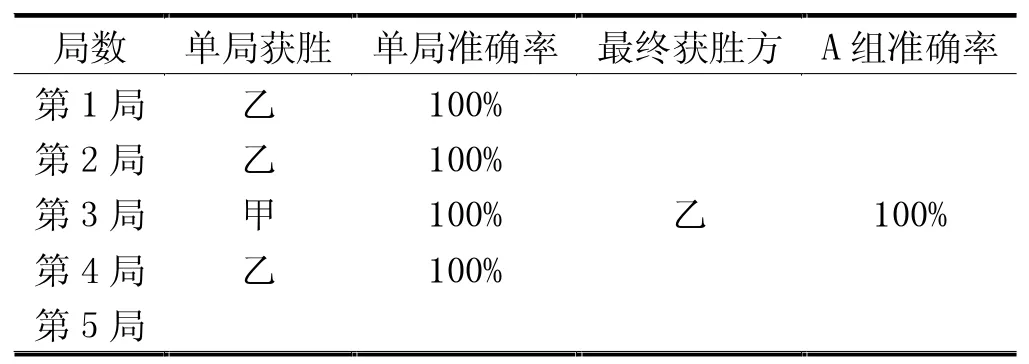
表2 B 组对弈情况表

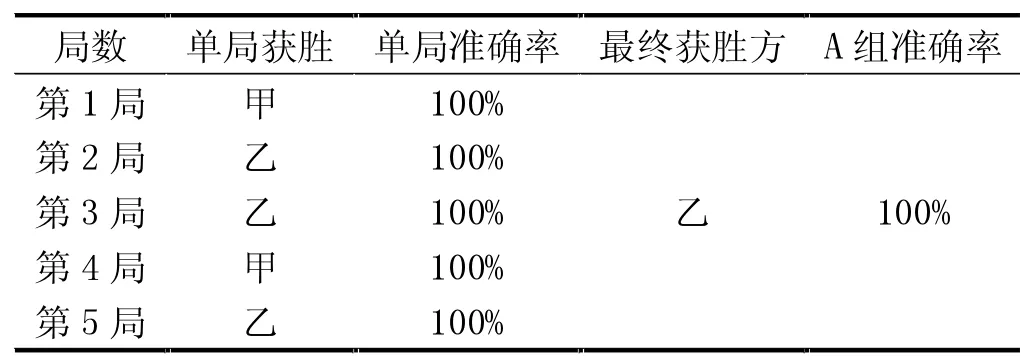
表3 C 组对弈情况表

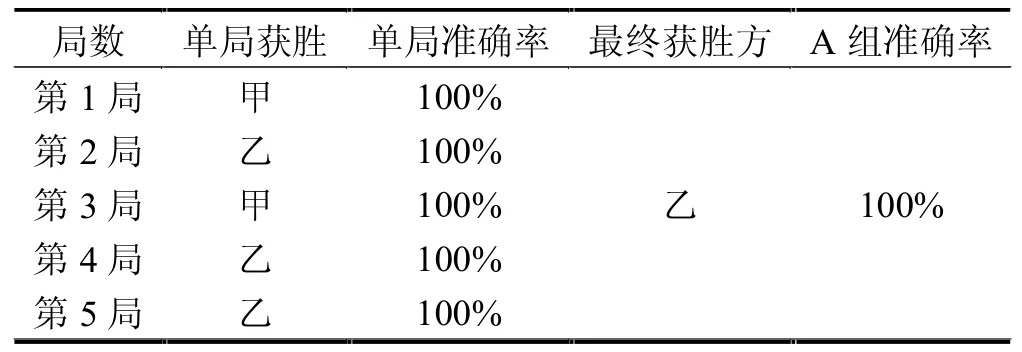
表4 D 组对弈情况表

表5 E 组对弈情况表

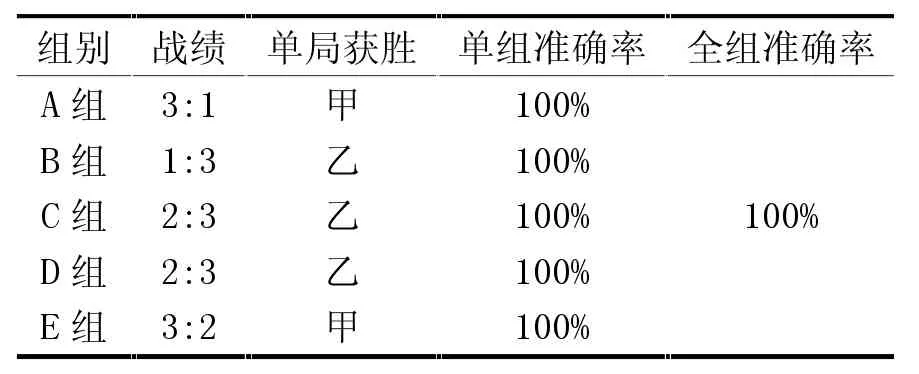
表6 5 组对弈情况汇总表

5 结束语

本系统突出软件应用与开发的创新性和实用性，使得人工智能、博弈论、计算机（机器）融合成为一个有机的整体。对于计算机博弈的研究来说，既能推动博弈论的发展，又能推动人工智能的发展。