基于航迹方向最大密度估计的红外多目标双站定位

岳 娟，李范鸣，高思莉*

（1. 中国科学院智能红外感知重点实验室，上海 200083；2. 中国科学院上海技术物理研究所，上海 200083）

1 引 言

红外双站定位，作为一种无源被动光电探测技术，通过两个红外成像测站对目标进行测向交叉定位［1］，获取目标三维位置，具有作用距离远、抗干扰性好、穿透烟尘雾霾能力强、全天时工作等优点［2］，在空间碎片等目标三维定位及预测、发射任务中目标辐射特性跟踪反演、军事威胁目标甄别与对抗以及打靶训练评估等军民用领域具有重要应用价值。

红外弱小目标一直是军民用领域重点感兴趣对象［3］，且常常伴有多目标处理任务。因此对于红外双站定位系统，须设计多目标匹配定位算法，才能获取各目标的三维位置。由于这类目标占据红外图像像素数少，且图像形状与纹理特征弱，无法适用于基于灰度［4］或基于特征［5］的传统匹配算法，多目标匹配难度大。如何提高多目标匹配定位精度，满足应用需求，是红外双站定位面临的一项重要研究难题。

目前，多站多目标任务［6-7］定位算法可大体分为两类：聚类法和数据关联法。聚类法适用于测站数量大于3 的定位系统，它基于多站多目标测向线两两相交交点的空间分布特性，通过不同的策略对交点集合进行聚类分析，确定交点分布密集的目标点的位置和数量［8-9］，消除虚假交叉点，实现多目标定位。数据关联算法主要用于判定各传感器的测量参数是否来自同一个目标，对于测向交叉定位系统，该方法主要是利用前两个测站的测向交叉点和第三个测站的测向角度值进行匹配检测，消除虚假交叉点［10］。

对于双站测向交叉定位系统，王成等［11］基于双站定位模型推导出来源于同一目标的测向角所满足的唯一方程，基于该方程定义关联残差与关联度，以衡量每组测量数据来源于同一目标的真实程度，实现两个测站多目标测量数据关联；王鲲鹏［12］将多视约束引入到双站多目标跟踪匹配中，将同名点匹配搜索范围从整幅图像缩小至核线上，进行两站点目标成像数据关联。上述两种方法都基于对极几何核心原理。对极几何，作为同名像点对满足的几何约束条件，是值得红外弱小多目标匹配定位借鉴的重要方向，但文献中尚未提及误匹配与测量误差处理办法。赵庆璐等［13］基于两站所有可能定位结果对应的距离与方位信息，构建多目标观测数据关联矩阵，在此基础上采用静态和动态相结合的方法滤除虚假航迹点。该方法的整体框架值得借鉴，但其静态滤除准则依赖于测站最大探测距离这一先验知识，且静态滤除的虚假点数量较少，然后再对候选关联进行滑窗跟踪，实现动态滤除，这在对空间相距很近的多目标定位时可能会遇到一定困难，也尚未提及测量误差处理办法。

王俊迪等［14］针对机载红外双站定位系统，提出基于岭回归的红外协同定位优化算法，利用岭回归算法求解出定位精度较高的两组测量子集的目标位置估计值，用以提高单目标定位精度，但尚未提及多目标匹配定位情况。

盛卫东等［15］立足天基分布式被动光学跟踪系统的多目标三维跟踪问题，采用两个观测平面与参考平面之间的倾角差（Hinge Angle Difference，HAD）作为数据关联准则，判断两条角轨迹是否来自于同一个目标，实现双星关联。HAD本质上是双站观测的立体几何约束，但当目标分布密集而出现多目标位于某测站同一观测方向或观测面上时，他们与另一测站的各目标HAD关联值都相同，多目标数据关联性能下降，对关联算法要求提高［16］。

Yang Yu 等［17］针对异步测向交叉定位传感器网络，提出一种基于时间特征的传感器测量数据关联方法，可用于空中目标雷达监视网络系统。该方法搜索满足时间差阈值约束的测量数据，对目标进行交叉定位，论文指出其方法优于HAD 方法，但是依赖于测量时间这一附加信息。

基于此，本文提出基于航迹方向最大密度估计的红外运动多目标双站定位方法。首先基于双站测向射线高程差进行单帧多目标初匹配，然后针对测量误差可能引起目标误匹配或定位位置偏差较大这一问题，充分利用目标三维运动航迹点的时空分布特点，基于Mean Shift 算法［18］进行目标航迹方向最大密度估计，以此进行航迹点真假检验，抑制测量误差对目标定位结果的影响，提高红外多目标三维定位精度。

2 算法思想

基于测向交叉定位原理，当多个目标同时出现在两个测站视场中时，会产生许多虚假交叉点。假设双站定位系统两个测站的视场中同时出现n个目标，测站通过目标检测算法可获得当前图像中所有目标观测数据{Oij|(xij，yij)，i=1，2；j=1，2，…，n}，(xij，yij)表示目标j在测站i的像点位置；从每个测站中任取一个观测数据，构成双站观测数据集合{(O1j，O2k)|(x1j，y1j，x2k，y2k)，j=1，2，…，n；k=1，2，…，n}，基于双站定位模型，可定位出n2个可能的目标位置；其中{(O1j，O2k)|(x1j，y1j，x2k，y2k)，j=k=1，2，…，n}是n个目标的双站观测数据，可定位出n个真实目标位置；其余n2-n个双站观测数据{(O1j，O2k)|(x1j，y1j，x2k，y2k)，j=1，2，…，n；k=1，2，…，n，且j≠k}，定位出n2-n个虚假目标位置。因此，须设计多目标双站匹配定位算法，消除虚假交叉点，筛选出目标位置，实现多目标定位。

如图1 所示，空间中存在P1、P2、P3三个目标，基于测站S1、S2对目标的成像观测数据，可确定6条观测射线。根据光电成像几何原理可知，观测射线S1P1与S2P1在空间上相交于物点P1，其高程差（定义见3.1 节）ΔZ11=0；观测射线S1P1与S2P2、S2P3在空间上都不相交，高程差ΔZ12＞0，ΔZ13＞0；且大概率情况下，物点距离越远，该高程差值越大。可见理论上，基于最小高程差可实现单帧多目标初匹配。该方法的核心基础也是双站观测的立体几何约束关系，但相比于基于面面关系的HAD 匹配关联方法，本文方法基于线线关系进行匹配关联，在计算量以及处理“多对一”问题上更具优势。

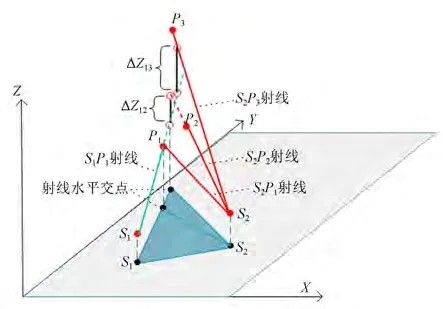
图1 双站多目标初匹配原理图Fig.1 Schematic of dual-station multi-target initial matching

实际应用中，由于测站定位、目标测向等各环节都会引入测量误差，这可能导致初匹配发生误匹配或定位结果偏差较大，进而影响目标三维位置估计与预测的准确性。假设测站定位、目标测向环节引入的噪声为独立的零均值高斯白噪声，以几何稀释精度（Geometric Dilution of Precision，GDOP［19］）为指标，对红外双站定位系统定位误差进行理论仿真，结果如图2 所示，图中星状离散点对应距离两站中心1.5 km 远处目标的定位误差，由此可知，该假设前提下，系统对1.5 km远处目标定位误差约1～1.4 m。此时对于空间距离约3 m 的两个物点，其对应的观测数据很可能发生误匹配，定位出目标虚假航迹点。因此，如何有效抑制测量误差，提高目标定位精度，是本文重点研究对象。

图2 本文双站定位系统GDOP 仿真结果Fig.2 Simulation result of GDOP for our dual-station positioning system

目标短时运动近似满足直线运动规律，尤其对处于非机动状态下的目标而言。假设通过连续多帧多目标匹配定位后，某目标形成N个参与三维航迹拟合的航迹点，其中M个航迹点为真实目标位置，N-M个航迹点为虚假目标位置（含误匹配点与定位偏差点，一般（N-M）≪M），则从M个真实目标航迹点中任取两点组成C2M个三维向量，其方位角与俯仰角大小接近，近似于目标实际三维航迹的方位角与俯仰角，分布比较集中；而从N个航迹点中任取其他两点组成(C2N-)个三维向量，其方位角与俯仰角大小不一，分布比较离散。 其中航迹点A(XA，YA，ZA)、B(XB，YB，ZB)，构成三维航迹向量，该向量的方位角θ、俯仰角β定义如下：

因此，基于目标三维航迹点这一时空分布特点，在多目标初匹配的基础上，对目标短时运动航迹方向进行估计；基于目标航迹方向估计结果，可对目标航迹点进行真假检验，采用最小二乘法对目标真实航迹点进行三维拟合［20］，结合目标运动特性即可对初匹配中定位误差较大的目标位置进行修正，以抑制测量误差对目标定位结果的影响，提高目标定位精度。

3 算法内容

3.1 双站多目标初匹配

对于三维空间中任意两条直线，本文定义它们在水平投影交点处的高程差为两直线的高程差。

双站定位系统中两站观测射线的高程差，只需在基于水平投影与左右测站俯仰模型［21］进行定位计算的基础上，增加一次线性运算与一次取绝对值运算：

首先，将测站S1对目标Pj以及测站S2对目标Pk成像观测的像点数据(x1j，y1j，x2k，y2k)转换成测向数据(θ1j，β1j，θ2k，β2k)［21］。其中，目标测向方位角θ限定为：水平投影平面中从正北方向偏移至观测方向的角度，取值范围为（-180°，180°］，顺时针方向偏移为正，逆时针方向偏移为负；

然后，基于水平投影模型，通过水平投影面上观测射线l1、l2求交，求得交点水平坐标（Xjk，Yjk)：

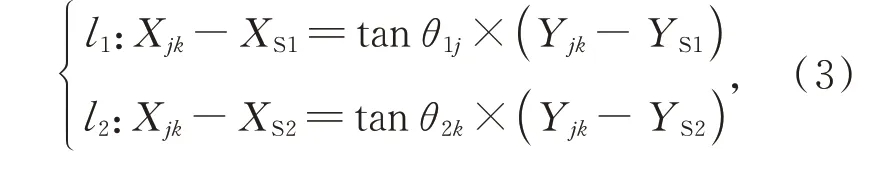
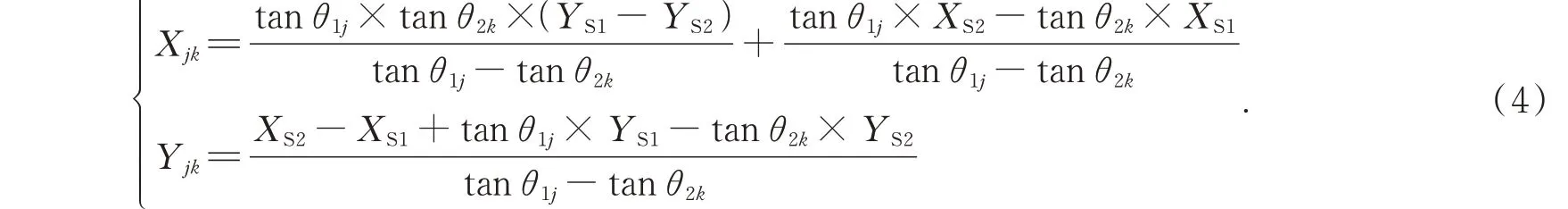
最后，基于左右测站的俯仰模型，获得水平投影交点对应左右测站观测射线上物点的高程值Z1j、Z2k，以及(O1j，O2k)匹配定位评价标准高程差ΔZjk：

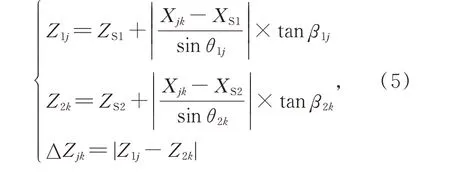
其中，(XSi，YSi，ZSi)是测站i在定位坐标系下的三维位置，由其GPS 坐标转换而来［22］。

本文基于观测射线高程差最小值搜索进行单帧双站多目标初匹配：假设两个测站同时对n个目标进行成像观测，对于测站S1的第j个目标观测数据，其与测站S2的n个观测数据依次进行匹配定位计算，得到n个高程差{ΔZjk|k=1，2，…，n}；搜索该高程差集合最小值，其对应的测站S2目标，即为测站S1目标j初匹配结果，记为jS2，则有：

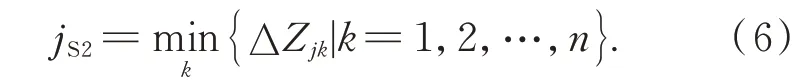
然而，实际应用中，测站定位、目标测向等环节都不可避免地引入测量误差，这使得即使观测像点对(O1j，O2k)来自同一个目标，也可能会出现Z1j≠Z2k，ΔZjk＞0；尤其在很多应用场景下，多目标空间位置接近，或者受相机透视变换的影响，多目标投影的像点位置相距很近甚至重叠，此时由于测量误差的存在，基于式（6）进行单帧多目标匹配定位很可能会出现误匹配点或定位偏差点。因此，如何有效抑制测量误差对初匹配定位结果的影响，提高多目标定位精度，是本文重点研究对象，抑制方法如后文3.2～3.4 节所述。

3.2 基于方向二维直方图的目标航迹方向初估计

本文基于目标短时运动三维航迹方向二维直方图，进行航迹方向初估计。从目标初匹配定位的航迹点中任取两点，构成三维航迹向量，将航迹向量的方位角θ、俯仰角β在取值范围内进行区间划分、统计，可获得目标三维航迹向量方向二维直方图。

若 将 (θ，β) 取 值 范 围（θ∈(-90，90]，β∈(-90，90]）均分为18×18 个统计区间，搜索该方向二维直方图最大值，记录该最大值对应的直方图索引为(ii*，jj*)，则其对应目标航迹方向估计范围如下式所示。

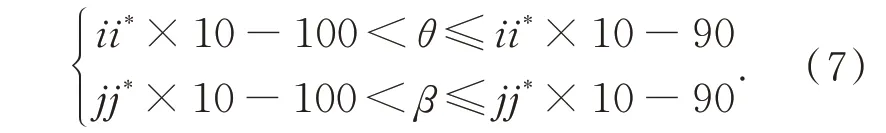
统计满足式（7）的目标所有航迹向量方向(θi，βi)的均值，即为目标航迹方向初估计结果(θc0，βc0)，如下式所示，K表示满足（7）的目标航迹向量数量。

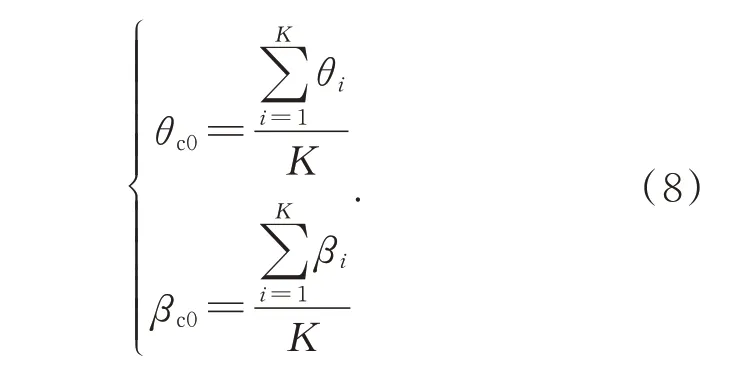
式（7）对应的方向区间在一定程度上描述了目标三维航迹方向最大密度分布区间，但是基于该区间直接进行定位误差抑制，存在两点局限性：

其一，当目标航迹向量方向集中分布在直方图两个区间交接处时，易将有效匹配点误判为虚假点。某目标三维航迹点及其方向二维直方图如图3 所示，其三维航迹方向分布图如图4 所示。目标航迹向量方向集中分布在直方图两个区间交接处，方向二维直方图上出现两个高峰，图4 中黑色矩形区域为该目标方向二维直方图最大值区间，图中红色点为该目标第1～10 个航迹点与其他航迹点组成的三维向量的方向角分布，绿色点、蓝色点分别为该目标第11、12 个航迹点和其他航迹点组成的三维向量的方向角分布。由于第11、12 个航迹点相应的方向角主要分布在目标方向二维直方图最大值区间以外，故它们均被判定为测量误差引起的虚假航迹点。而从图3 可以看出，目标第11 个航迹点是理想航迹点；

图3 某目标航迹及方向二维直方图Fig.3 Diagram of target track and 2D histogram of direction

其二，方向二维直方图最大区间搜索结果易受取值区间划分方式影响，不具备目标航迹方向平移不变性。若在θ∈( -85，85]，β∈(-90，90]取值范围内，进行17×18 个区间统计，则图4 所示目标第1～12 个航迹点都位于方向二维直方图最大值区间，导致目标第12 个定位误差较大的航迹点未被有效抑制。

可见，基于方向二维直方图最大值搜索不足以很好地描述目标三维航迹方向。如第2 节所述，考虑到目标真实航迹点构成的航迹向量方向角分布比较集中，而包含有较大定位误差的航迹点的航迹向量方向角分布比较分散，如图4 某目标三维航迹方向整体与局部分布图，红色与绿色点分布集中，而蓝色点分布离散，本文提出基于Mean Shift 的目标航迹方向最大密度估计方法，以此进行初匹配定位误差抑制。

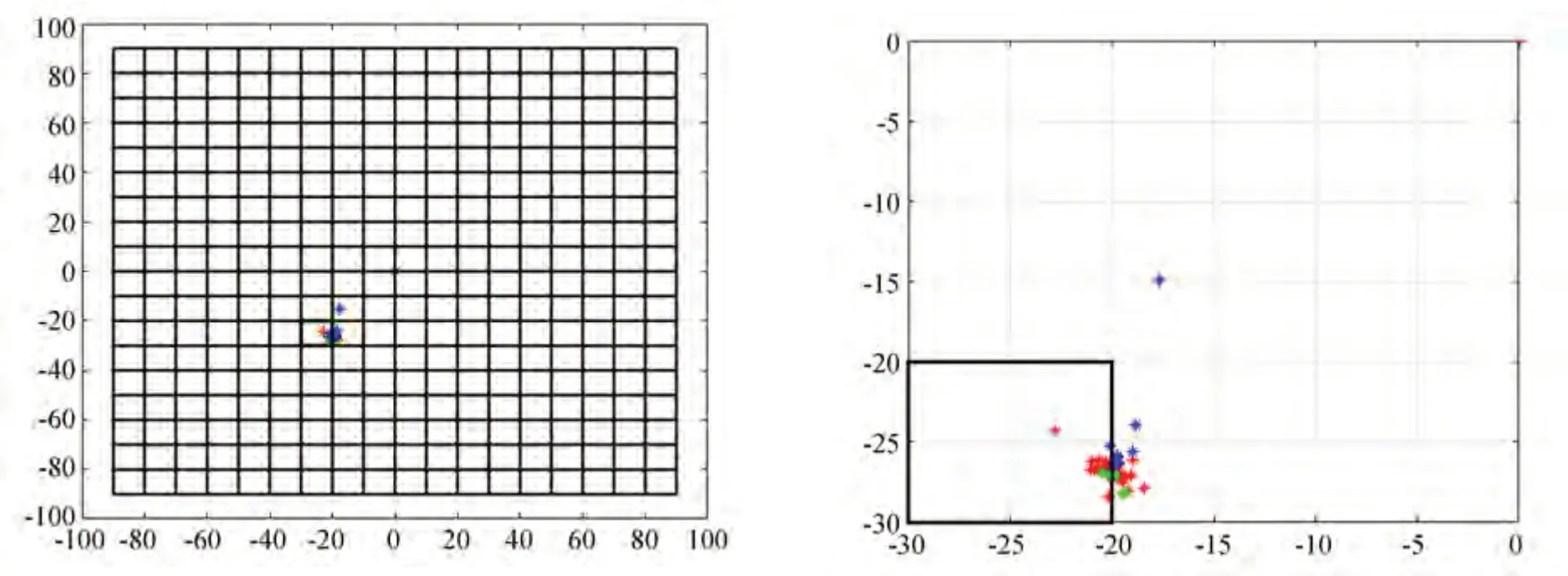
图4 某目标三维航迹方向分布图Fig.4 3D track direction distribution map of a target

3.3 基于Mean Shift 的目标航迹方向最大密度估计

Mean Shift 算法是一种基于密度梯度的无参数估计方法。本文提出基于Mean Shift 的目标航迹方向最大密度估计方法，该方法以方向二维直方图最大值搜索的目标航迹方向初估计结果(θc0，βc0)为起点，以保证算法收敛至全局最优解；以高斯核函数为权重进行Mean Shift 向量估计，给不同距离的方向样本分配不同的高斯权重，削弱远处方向样本的影响；经多次迭代，不断靠近目标三维航迹方向二维分布密度最集中的区域，最终搜索出目标航迹方向的最大密度区间(C，r)，其中C为最大密度区间样本中心(θc，βc)，r为区间半径（对应Mean Shift 算法搜索半径），则最大密度区间可描述为：

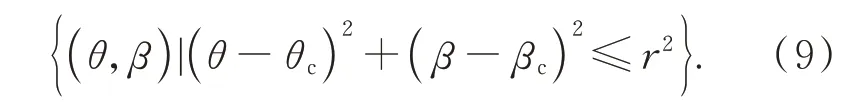
该算法流程可简单描述如下：

（1）参照式（10）进行Mean Shift 向量m(x)估计，其中k为Mean Shift 感兴趣区域内的方向样本数量；xi为感兴趣区域内的目标三维航迹向量方向样本；x为当前感兴趣区域中心，初始值为(θc0，βc0)；GH( )· 为权重高斯核函数，σ为高斯核因子；

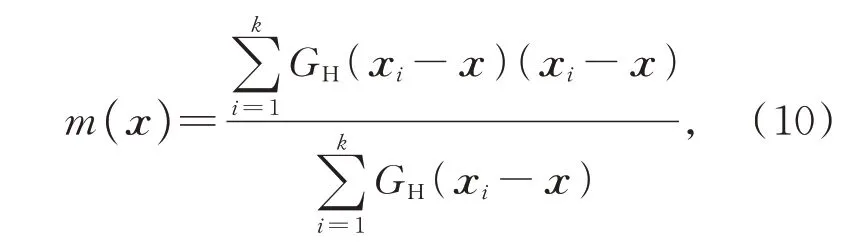
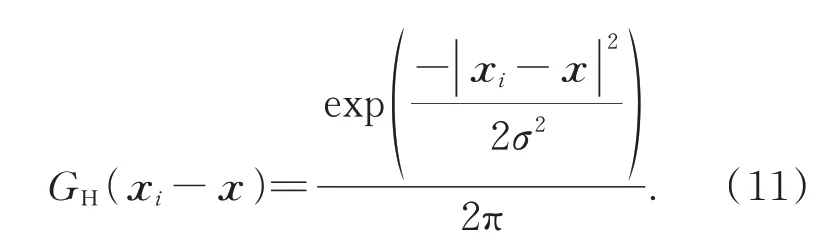
（2）将Mean Shift 窗口移动m(x)；

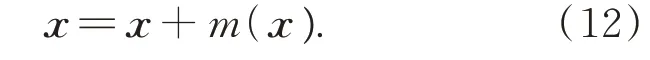
（3）返回（1），直到移动距离满足下述收敛条件。

3.4 基于航迹方向最大密度估计的误差抑制

对于目标航迹点P，若它与其他航迹点组成的三维航迹向量的方向角多数满足式（9），则判定P为目标有效的真实航迹点；反之，则判定P为无效的虚假航迹点。

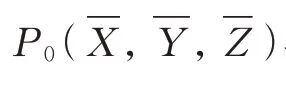
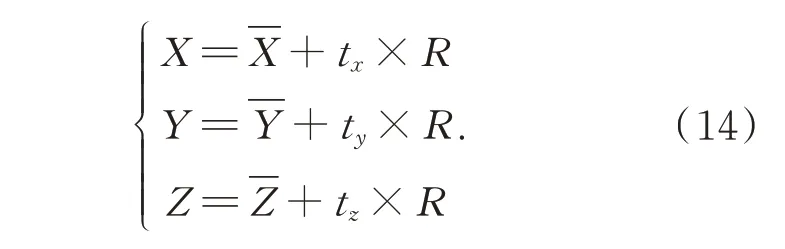
在此基础上，结合目标运动特性，修正虚假航迹点位置，提高目标估计及预测精度。比如，根据目标第m、n帧有效航迹点Pm(Xm，Ym，Zm)、Pn(Xn，Yn，Zn)，基于目标短时匀速直线运动假设，可估算出第k帧航迹点位置Pk(Xk，Yk，Zk)；基于地面高程Ze，可预测目标落点位置Pf(Xf，Yf，Zf)：

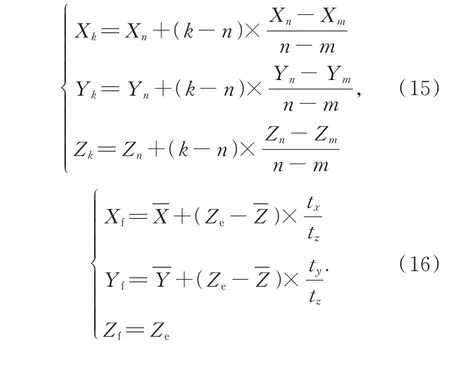
4 实验与结果

本文将图5 所示红外双站定位系统安装于某靶场两个观测塔上，对飞行打靶训练进行成像观测，获取多目标定位实验数据。其中两个红外相机均为320×256规格，测角精度均为0.33 mrad，测站S1（GPS（113.342 923 556°，40.819 074 233°，1 293.353 m），测站S2（GPS（113.309 160 893°，40.819 595 229°，1 285.775 m）），测向参考点GPS （113.322 337 925° ，40.808 994 975° ，1 255.81 m），参考点像点位置分别为S1（160，183）、S2（160，180）。

图5 红外双站定位系统Fig.5 Infrared dual-station positioning system

本文多目标定位对比实验流程图如图6，其中，直接法表示直接基于3.1 节初匹配结果对目标进行三维定位；直方图法表示基于方向二维直方图最大值搜索进行误差抑制（参照3.4 节）。本文不关注单站红外图像目标检测与关联算法，重点研究基于成像观测数据进行多目标匹配定位。

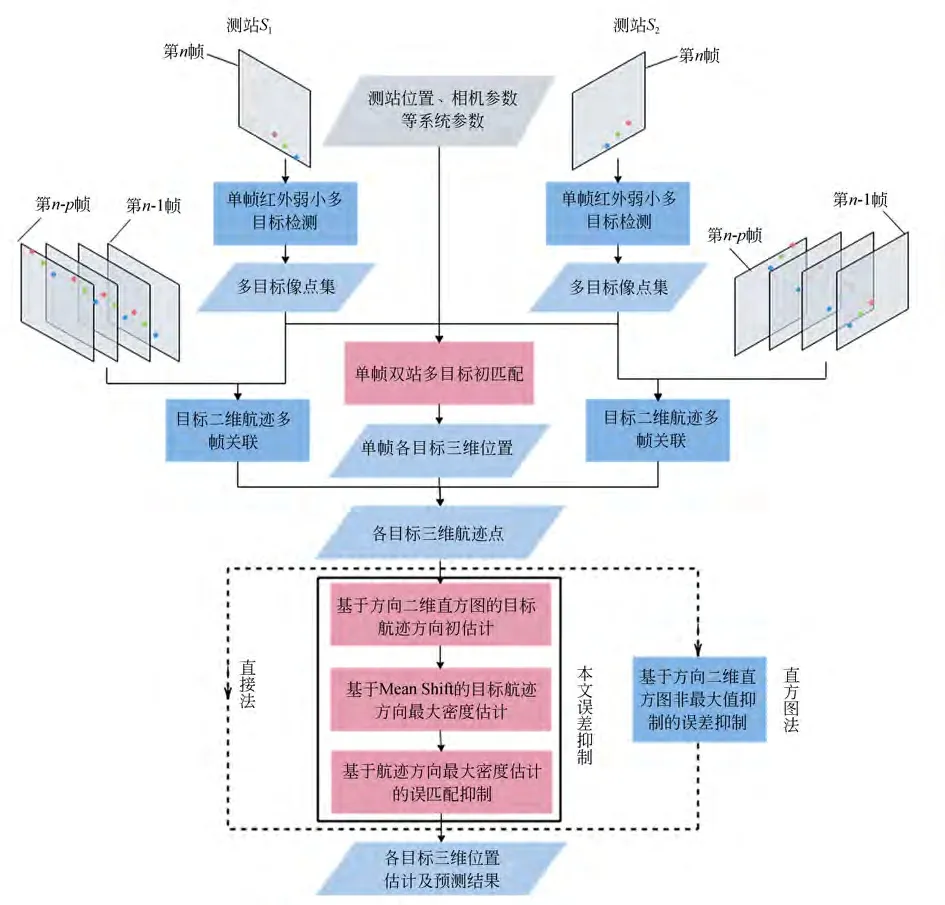
图6 实验流程图Fig.6 Flowchart of experiment

4.1 多目标初匹配

如图7 和表1 所示为定位系统对某一十弹连续打靶训练观测的两帧红外成像及目标观测数据，由图可知，目标10 在第12 帧已落地爆炸，导致其图像位置检测不准，引入较大测向误差。

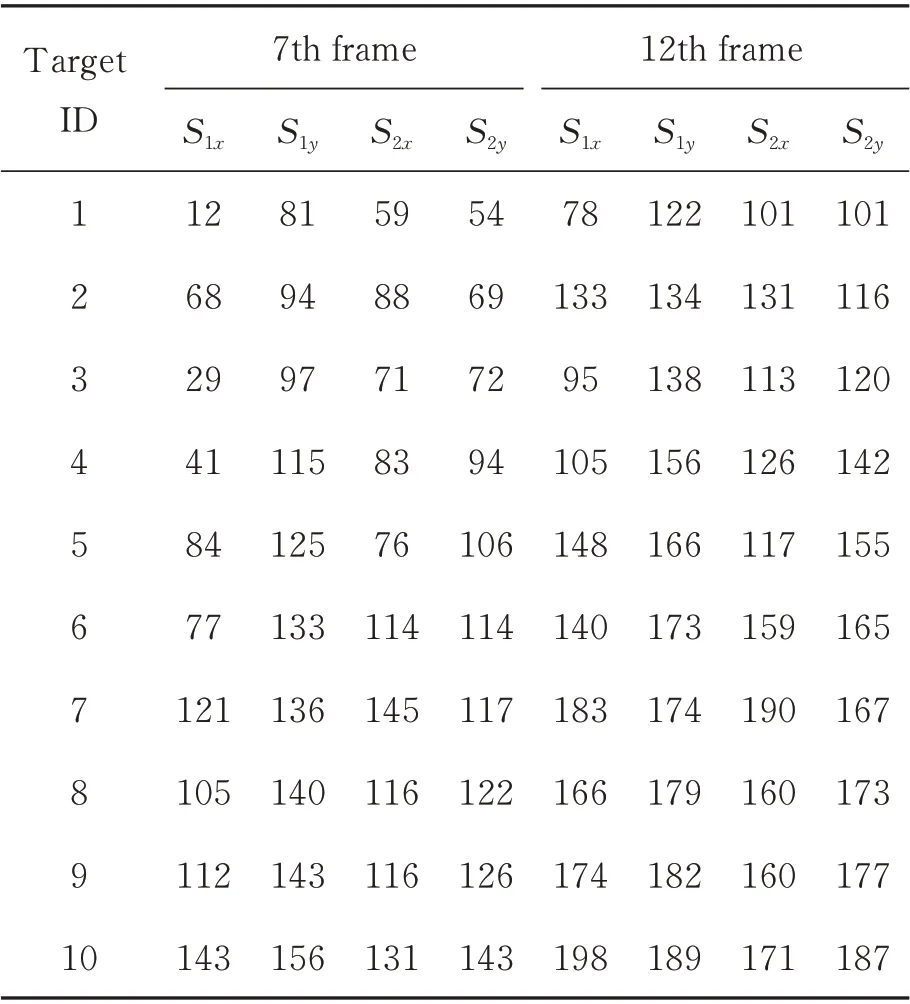
表1 多目标观测数据Tab. 1 Observation data of multi-target

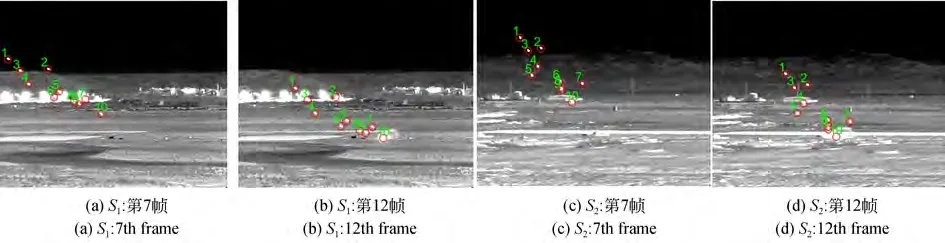
图7 多目标红外成像数据Fig.7 Infrared imaging data of multi-target

本文基于该定位系统连续17 帧成像观测数据进行多目标初匹配，获得各目标17 个航迹点初始定位位置，其中目标3、7 和10 的航迹点初始定位位置及其最小二乘拟合结果如图8 所示，图中蓝色离散点为目标航迹点；外加绿色小框的航迹点表示被判为有效的目标航迹点，参与目标航迹拟合；红色方框内是由某个测站观测数据缺失引起的明显奇异值点，不会参与目标航迹拟合，观测数据缺失原因可能是目标能量弱、被遮挡、已落地等。由图可知，目标3 无误匹配点或误差偏差较大的定位点，初匹配误差较小；目标7 第4、7个航迹点发生误匹配，它们的定位结果明显偏离目标运动航迹，引起拟合航迹偏离实际航迹位置；目标7 的第15 个航迹点与目标10 的第12 个航迹点，虽然没有发生误匹配，但由于落地后目标图像位置检测不准，引入较大测向误差，进而引起初匹配位置有较大偏差。

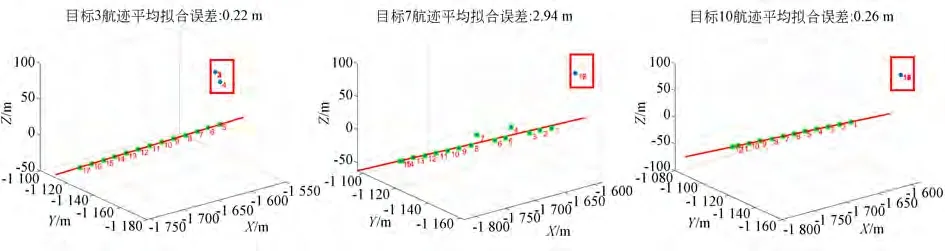
图8 目标3、7 和10 初匹配定位及航迹拟合结果Fig.8 Initial matching positioning and track fitting results of the 3rd，7th and 10th target

表2 为第7 帧S1站目标7、10 与S2站10 个目标匹配定位结果，可见基于式（4）进行初匹配时，S1站目标7 会错误匹配至S2站目标8；而目标10正确匹配，但因测向误差较大，其初匹配点成为误差偏差点。

表2 多目标匹配定位结果Tab.2 Positioning results of multi-target matching（m）

可见，目标3、7 和10 分别对应三类具有代表性的目标：无误匹配点或误差偏差较大定位点；既有误匹配点又有误差偏差较大定位点；虽没有无误匹配点但有误差偏差较大定位点。因此，为了提高目标三维位置估计与预测精度，须进一步进行误差抑制，降低测量误差对诸如目标7、10 的定位影响。

4.2 误差抑制

4.2.1 效果评价

现有实验条件下，无法获得目标运动航迹点真实位置，但目标短时运动航迹拟合结果是目标真实位置估计与预测的依据，其拟合精度也很好地反映了误差抑制效果。因此，本文从目标航迹拟合效果直观图和评价指标两方面进行误差抑制效果评估。

引入目标航迹点P拟合误差ε，描述P偏离拟合航迹(P0，T)的直线距离，计算如下：

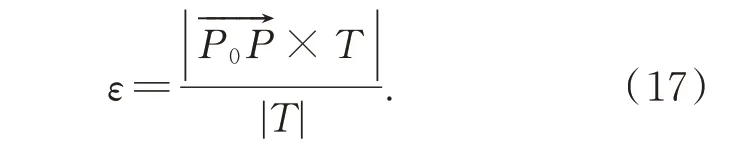
引入目标航迹平均拟合误差εˉ，描述所有参与航迹拟合的目标航迹点{P}偏离拟合航迹(P0，T)的平均直线距离，card(·)表示集合中元素个数，计算如下。

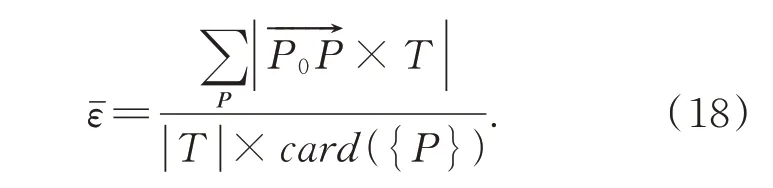
4.2.2 实验结果

首先，基于方向二维直方图进行目标航迹方向初估计。如图9 与图10 所示分别是目标3、7 和10 的方向二维分布图与二维直方图，在此基础上，参照3.2 节内容可实现航迹方向初估计。测量误差引入的位置偏差点，使目标10 直方图上出现两个明显峰。

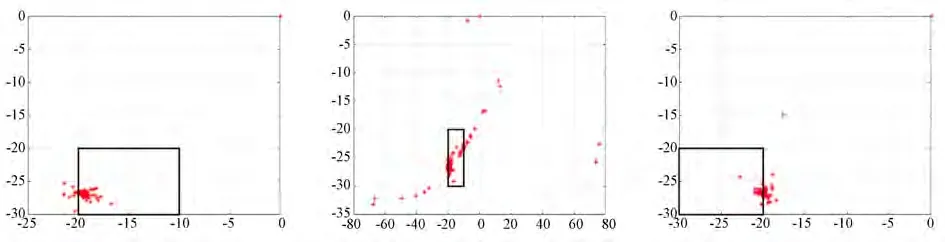
图9 目标3、7 和10 航迹方向二维分布及最大值区间Fig.9 2D distribution and maximum range of track direction of the 3rd，7th and 10th target

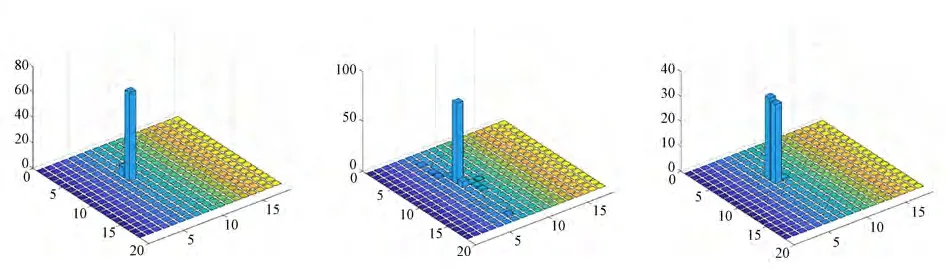
图10 目标3、7 和10 方向二维直方图Fig.10 2D histogram of direction of the 3rd，7th and 10th target

然后，进行基于Mean Shift的目标航迹方向最大密度估计。搜索半径0.8 m，迭代门限0.1 m，高斯核因子20，如图11 所示是目标3、7 和10 航迹方向最大密度区域估计结果，对应的收敛区间中心分别为（-19.460 1，-26.891 9），（-19.170 4，-26.561 3）和（-20.090 6，-26.730 4）。

图11 基于Mean Shift 的目标3、7 和10 航迹方向最大密度估计Fig.11 Maximum density estimation of track direction of the 3rd，7th and 10th target based on Mean Shift

最后，进行误差抑制对比实验及分析。直方图法及本文法误差抑制后航迹拟合效果分别如图12 与图13 所示，综合对比图8 直接法航迹拟合效果可知：两种算法都能很好地抑制误匹配点，其拟合航迹不再明显偏离真实航迹位置；但直方图法不能抑制误差偏差点，如目标7 的第15 个航迹点与目标10 的第12 个航迹点；而本文方法可以抑制误差偏差点，后续可基于航迹拟合结果，结合目标运动特性，修正误差位置偏差点，提高目标估计及预测精度，如图所示箭头所指位置为本文方法修正的落点位置，修正距离分别为3.1 m 和1.8 m。

图12 基于直方图法的目标3、7 和10 航迹拟合Fig.12 Track fitting of the 3rd，7th and 10th target based on method of histogram

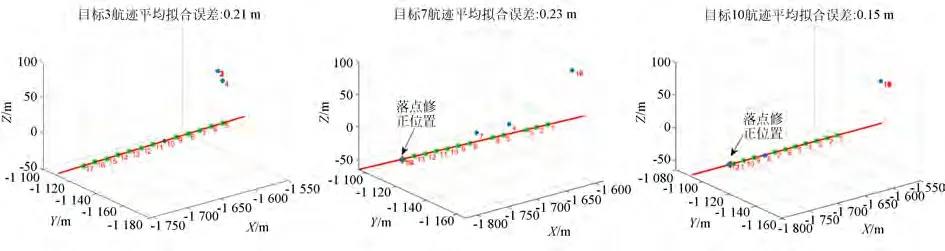
图13 基于本文方法的目标3、7 和10 航迹拟合Fig.13 Track fitting of the 3rd，7th and 10th target based on proposed method

如表3 所示为三种方法目标航迹拟合误差，表中-1.00 表示该航迹点被判定为奇异值点、误匹配点或误差偏差点等无效航迹点，不参与航迹拟合。由表中各航迹点拟合情况可知：直接法无法区分目标有效航迹点与误匹配点、误差偏差点，不能抑制测量误差；直方图法可以很好地抑制误匹配点，但不能有效抑制误差偏差点，如它没能抑制目标7 第15 个航迹点，同时，虽然它抑制了目标10 第12 个航迹点，但如前文3.3 节分析，若重新限定直方图区间范围，它也不能抑制该定位偏差点；本文方法既能抑制目标7 的两个误匹配点，也能抑制上述两个定位偏差点，误差抑制能力更强。由表中拟合误差可知：三种方法的目标最大拟合误差分别为11.10 m，1.05 m 和0.43 m，三种方法对最具代表性的目标7 的平均拟合误差分别为2.94 m，0.31 m 和0.23 m。

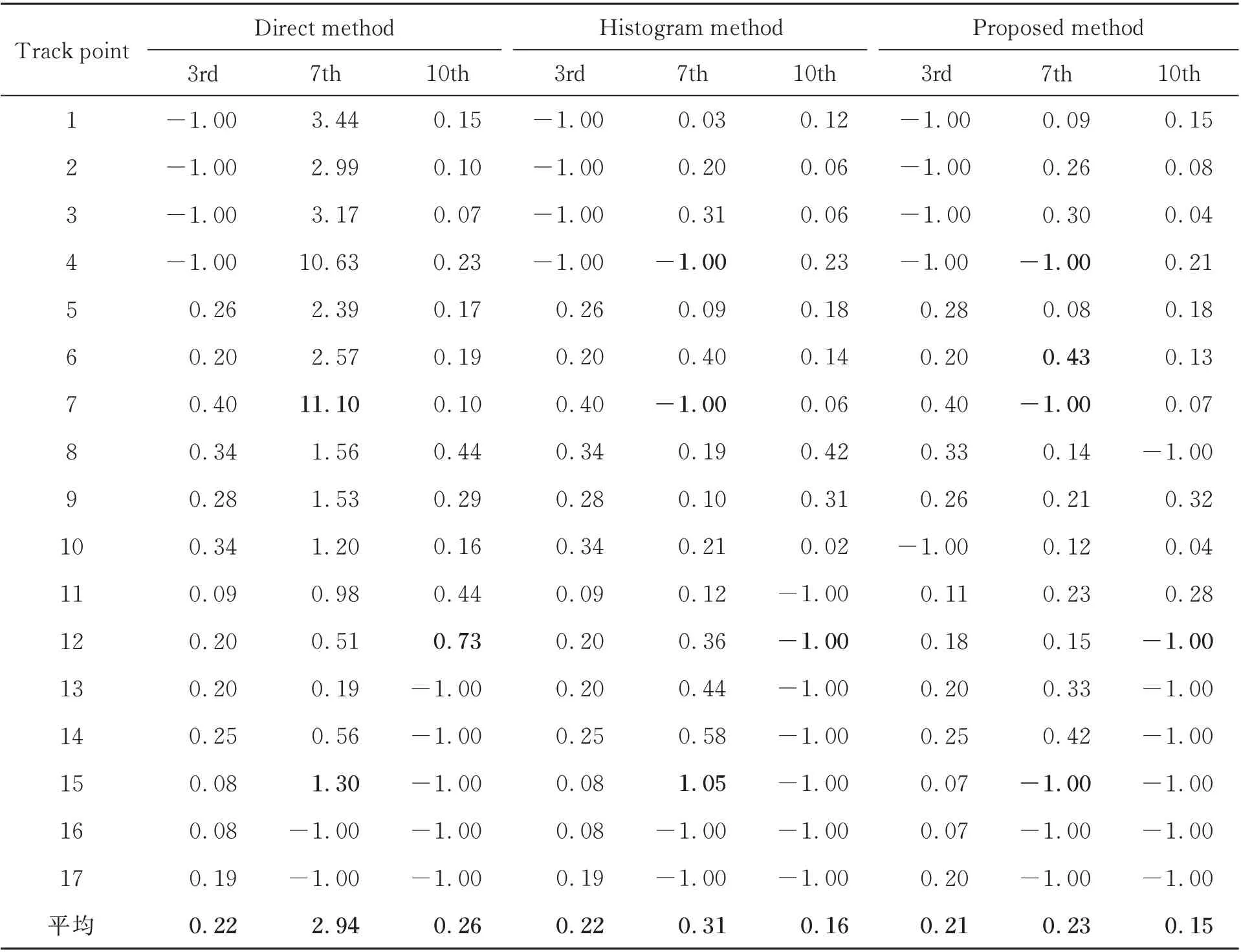
表3 各目标航迹拟合误差Tab.3 Fit error for each target track（m）

综上，本文提出的基于航迹最大密度估计的红外运动多目标双站定位方法，既能有效剔除误匹配点，又能抑制误差偏差点；相比于直方图法，本文方法最大拟合误差降低59%，平均拟合误差可降低26%，具有应用价值。

5 结 论

为了抑制测量误差对红外多目标双站定位的影响，本文充分利用目标三维运动航迹点的时空分布特点，提出了基于航迹最大密度估计的红外运动多目标双站定位方法。该方法首先基于双站测向射线高程差进行单帧多目标初匹配；然后，开展基于Mean Shift 的目标航迹方向最大密度估计，以方向二维直方图最大值搜索结果为起点，进行最大密度搜索估计，以避免直方图法局限性，且能保证Mean Shift 算法迭代收敛至全局最优解；最后，基于目标航迹方向估计结果，进行航迹点真假检验，采用最小二乘法对有效的目标真实航迹点进行三维拟合，结合目标运动属性进行目标三维位置估计与预测，抑制测量误差对目标定位结果的影响。实验结果表明：本文方法不仅能有效剔除误匹配点，而且能抑制误差偏差点；航迹最大拟合误差小于0.5 m，平均拟合误差小于0.3 m，优于其他算法；对于代表性强的目标7，直方图法航迹最大、平均拟合误差分别为1.05 m、0.31 m，而本文方法相应误差分别为0.43 m、0.23 m，最大拟合误差降低幅度大于50%，平均拟合误差降低26%。可见，本文方法能有效抑制定位误差，在空间碎片等目标三维定位及预测、发射任务中目标辐射特性跟踪反演、军事威胁目标甄别与对抗以及打靶训练评估等军民用领域具有重要价值。