机床主轴热误差通用型温度敏感点组合选取

（1. 西南交通大学机械工程学院，四川 成都 610031；2. 浙江大学流体动力与机电系统国家重点实验室，浙江 杭州 310027；3. 四川大学机械工程学院，四川 成都 610065；4. 重庆遨博智能科技研究院有限公司，重庆 400050；5. 衢州学院浙江省空气动力装备技术重点实验室，浙江 衢州 324000）

1 引 言

机床作为制造业生产的“母机”，其发展程度直接影响着国家工业的发展水平［1］。提高机床的加工精度，对发展高精密数控加工技术和制造业具有重要意义。影响机床加工精度的因素主要有以下几方面：由机床本身设计缺陷或零部件相对运动引起的几何误差、机床受热变形影响导致的热误差、加工过程中切削力变化导致的切削力误差以及其它误差［2］。在这些误差中，热误差是导致机械零部件几何误差的主要原因，约占总误差的40%～70%［3-5］。

热误差补偿法是提高机床加工精度的经济有效的手段，其核心在于建立具有强鲁棒性和高预测性能的热误差模型对热误差进行预测和补偿［6-9］。热误差模型以温度敏感点处测得的温度变量为输入，以热变形量为输出，其中温度敏感点组合的选取直接影响着模型的训练精度和预测效果。温度变量过多，会加大实验成本与工作量，同时温度变量间的耦合现象会影响建模精度；温度变量过少，则会由于缺乏引起热误差的关键信息而削弱模型的鲁棒性、降低模型的预测性能。因此，在热误差建模之前进行温度敏感点的选取是至关重要的一步［10］。

多种方法可用于温度敏感点的选取，Abdulshahed 等［11］基于灰色模型和模糊C-均值聚类算法，采用一种像素的局部平均模式从热图像中识别不同组的温度敏感点，从而提高模型输入的质量。Longstaff 等［12］采用自适应神经模糊推理系统将温度数据空间划分为多个矩形子空间，并根据灰色理论得出所有的温度传感器对热误差的影响排序，然后基于模糊C-均值聚类方法对各温度的影响权重进行分类。Tsai 等［13］首先采用奇异值分解方法过滤各温度测点，消除温度测点之间共线性的影响。然后根据主成分分析方法计算的温度点和热误差之间的相关系数进行排序和筛选得到温度敏感点组合。Tan 等［14］提出一种最小绝对收缩算子选择法直接选取温度敏感点集合。Liu 等［15］使用相关系数法选取温度敏感点组合，提升了热误差模型的鲁棒性与预测精度。

近年来，神经网络建模方法以其良好的非线性映射能力与较强的计算能力被广泛应用于热误差建模研究中，多种参数优化算法与神经网络相结合的热误差建模方法应运而生［16］。Ma 等［17］结合模糊聚类和相关分析对典型温度变量进行了分组优化，采用遗传算法和粒子群算法（Particle Swarm Optimization，PSO）对反向传播（Back Propagation，BP）神经网络参数进行优化。Santos 等［7］使用变分模式将误差数据分解为几个固有的模态函数组件，并使用灰狼算法对长短时记忆神经网络的超参数进行优化，经验证，提出的VMD-GW-LSTM 热误差模型具有较强的鲁棒性和较优的泛化能力；此外，Liu 等［18］利用遗传算法优化小波层数和乘积层数以及自回归小波神经网络的权值。Yin 等［19］人将物理模型与数据驱动模型相结合，从预测的温度场出发，设计了一种人工神经网络算法，以提高主轴热误差预测的精度。Liu 等［20］提出了使用深度信念网络和蒙特卡罗方法计算模型可靠性的方法，使用深度信念网络替代了隐函数，确定了单参数、多参数波动模型的可靠性和残差预测，并通过实验验证了模型的鲁棒性和所提出的可靠性计算方法的准确性。

上述温度敏感点选取方法普遍将温度变量优化至10 个以内，有效地精简了温度敏感点数量，提高了建模效率与预测精度。但其中温度敏感点数目皆凭借研究者的工程经验直接指定，难以自动确定。针对上述问题，本文以VMC850 五轴立式数控加工中心为对象进行热误差实验以及温度场与热误差的测量；提出一种通用性温度敏感点组合选取方法，从一系列包含不同聚类数目的温度变量组合中自动选取适用于热误差预测的最优的温度敏感点组合。经过验证，选取的最优温度敏感点同时适用于不同工况下主轴各项热误差的预测，且在不同的热误差模型中具有良好的通用性。首先介绍了温度敏感点组合选取的相关理论以及机床温度场和主轴热误差的测量实验，包括测量仪器的安装和数据的获取；其次提出了基于数目自动确定的通用型温度敏感点组合选取方法，并以某一工况下的实验数据为例选取最优温度敏感点组合；然后对最优温度敏感点组合在不同工况下主轴各项热误差的预测中的有效性进行验证，并建立RBF、SVM 与MLR 热误差模型，对最优温度敏感点在不同类型的热误差模型中的通用性进行验证。

2 温度敏感点选取相关理论与热误差实验

2.1 温度敏感点选取相关理论

2.1.1 K-Means 聚类算法

传统的K-Means 聚类算法因其在数据处理中的高效性而被广泛应用于数据聚类中，但该算法随机选取初始聚类中心的方式会导致聚类结果不稳定。针对这一情况，Arthur 等［21］首次提出一种改进的K-Means++聚类算法。相比于K均值算法，其最大的特点是初始聚类中心的选取方式不同：首先确定聚类数目K并随机选取一个数据点作为第一个初始聚类中心；其余初始聚类中心由剩余数据点与当前已有初始聚类中心的欧式距离决定，距离越远者被选作下一聚类中心的概率越大。这一改进有效提升了聚类结果的稳定性。本文采用K-Means++算法对温度测点进行聚类，主要步骤如下：

（1）指定聚类数目K并随机选取一个温度变量作为第一个初始聚类中心I1；

（2）计算每个温度变量离当前聚类中心的最远距离，用D（Xi，Ij）表示；采用轮盘法选取下一个聚类中心，D（Xi，Ij）越大，该温度变量越容易被选择为下一个聚类中心；

其中：Xit为温度变量，Ijt为当前距X最近的初始聚类中心，m为温度数据的样本数，i=1，2…29，j=1，2…k。

（3）重复（2），直至选出K个初始聚类中心｛I1，I2，…Ik｝。

（4）剩余算法步骤与标准的K-Means 算法一致。

2.1.2 相关性分析

相关系数反映了变量间的相关程度。本文采用皮尔逊（Pearson）相关系数来衡量各温度变量与热误差的相关程度。两个连续变量的皮尔逊相关系数等于它们之间的协方差除以它们各自标准差的乘积。系数的取值总是在-1 到1 之间，其绝对值越接近1，变量间的相关性越强。Pearson 相关系数的计算公式如下：

其中：RXY表示样本的Pearson 相关系数，SXY表示X与Y之间的协方差；SX表示温度样本X的样本标准差，SY表示热变形量样本Y的样本标准差，N为样本数量，Xˉ表示各温度变量的平均值，Yˉ表示各热误差变量的平均值。

2.1.3 BP 神经网络

BP 神经网络是一种按误差反向传播训练的多层神经网络。近年来，由于其具有任意复杂的模式分类能力和优良的多维函数映射能力在机床主轴热误差建模中应用广泛且效果较好［22-24］。从结构上来看，BP 神经网络由输入层、隐藏层和输出层组成。从算法本质上讲，BP 算法以误差为目标函数、采用梯度下降法来计算目标函数的最小值。本文将使用具有一层输入层，一层隐含层和一层输出层的BP 神经网络热误差模型进行最优温度敏感点的选取与最优温度敏感点组合有效性的验证，其网络结构如图1 所示，将敏感点温度数据和各项热误差作为输入X1，X2，…，Xn，经BP 神经网络训练，测试得到各项热误差预测结果Y1，Y2，…，Yk。

图1 反向传播神经网络结构图Fig.1 Structure diagram of BP neural network

2.2 热误差实验

热误差测量是热误差建模的前提和基础。本文的热误差测量实验在VMC850 五轴立式数控加工中心进行，参照ISO 230-3 中的五点法［25］进行测量仪器的布置安装与数据采集。图2 为VMC850 数控加工中心实验现场图。

图2 VMC850 加工中心实验现场Fig.2 VMC850 machining center test site

2.2.1 实验仪器布置

实验器材选用标准均按照ISO 230-3 国际标准中的热误差实验部分设定。采用PT100 温度传感器和DAM-PT16 温度采集板卡获取机床温度。为了完整地获取机床温度场信息，实验中将29 个温度传感器分布在机床的各个温度场区域，包括主轴区域、主轴箱区域、工作台区域与箱体区域，具体分布如表1 和图3（a）所示：T1、T2 与T4、T6 对称安装在主轴左右两边的上部与下部，T3 和T5 安装在主轴前后的中部；T7、T9～T13、T20～T22、T27 分布在主轴箱区域；T15、T17、T24 布置在箱体的后侧；T23、T28 安装在机床箱体左右两侧；T14、T16、T18、T19、T25、T26、T29 布置在工作台上的不同部位；T8 用于测量实验场地的环境温度。位移传感器采用Lion Precision 电容式位移传感器，安装位置如图3（b）所示。

图3 传感器布置Fig.3 Sensor location

表1 温度传感器具体分布Tab.1 Specific distribution of temperature sensors

2.2.2 实验数据获取

机床热特性试验中主轴转速类型可分为主轴转速变化图谱形式和与最大转速成一定比例的恒定转速形式［14］。为获取机床在多种工况下的热误差数据，实验按照设定转速进行热误差测量，实验工况设计如表2 所示。测量实验共分为四组，在主轴空转的状态下分别按照恒定转速2 000 r/min、2 500 r/min、3 000 r/min与5 000 r/min进行。在实验过程中温度测量值与主轴热变形量实时同步采集，采集时间从机床冷态开始至机床达到热平衡状态结束，采样间隔设置为5 s。本文主要针对实验中机床温升阶段进行研究。

表2 热误差实验工况设计Tab.2 Design of thermal error experimental conditions

图4（a）为2 500 r/min 转速下采集的某组数据的部分温度测量值变化趋势，图像呈现了机床在前210 min 内从冷态开始的温度升高阶段的部分温度传感器的数据，不同曲线代表不同区域的温度变化趋势。图4（b）为同转速下与温度数据同步采集的主轴5 项热变形数据。从图中可以看出，在开始测量的前210 min 内，主轴五项热误差都随着温度的升高而增大，其中Y2 和Z方向的热误差变化最明显。

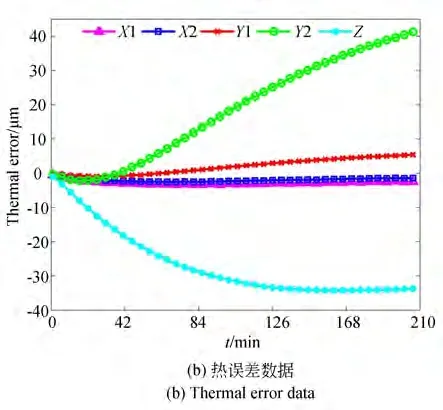
图4 2 500 r/min 转速下的部分温度数据与热变形Fig.4 Partial temperature data and thermal deformation at 2 500 r/min

3 基于数量自动确定的通用温度敏感点组合选取方法

本节详细介绍基于数量自动确定的通用温度敏感点组合选取方法，通过建立基于BP 热误差模型的绝对均方根误差与绝对残差均值评价指标从一系列不同数量的温度敏感点组合中自动选取性能最优的组合。以2 500 r/min 转速下采集的温度数据与Z向热误差数据为例对最优温度敏感点进行选取。

通用型温度敏感点组合自动选取法流程图如图5 所示。具体步骤如下：

图5 最优温度敏感点综合选取法流程图Fig.5 Flow chart of comprehensive selection method for optimal temperature sensitive points

（1）建立各温度变量与所有热误差项的绝对平均相关系数。

每个温度变量与五项热误差均存在一定相关性。若仅仅考虑温度变量与某一项热误差的相关性，可能会降低后期热误差模型预测性能的泛化性，故在进行相关性分析时应综合考虑各温度变量与五项热误差的相关程度。本文建立绝对平均相关系数（AR），即温度变量与五项热误差的皮尔逊相关系数的平均值表示该温度变量与五项热误差的相关程度。计算公式如式（3）所示。

其中：Rm，X1，Rm，X2，Rm，Y1，Rm，Y2，Rm，Z分别代表第m个温度变量与五项热误差的皮尔逊相关系数值，在本实验中m=1，2，3，…，29。

表3 所示为2 500 r/min 转速下29 个温度变量与五项热变形量的绝对平均相关系数计算结果。如表所示，在实验所布置的29 个温度传感器中，绝对平均相关系数最大值对应的温度变量为离加工区域较近的温度传感器T26，最小值对应箱体左侧区域的T23 传感器。

表3 2 500 r/min 转速下温度与热误差的绝对平均相关系数Tab.3 Absolute average correlation coefficient of temperature and thermal error data at 2 500 r/min speed

（2）设置温度传感器聚类数目范围［Kmin，Kmax］，根据绝对平均相关系数选取首个初始聚类中心，获取一系列K-Means++温度聚类组合。

根据机床机构特性的不同，参考ISO 230-7中热误差实验部分对温度传感器进行布置。为避免模型出现欠拟合现象，聚类数目不能过少；为有效消除温度传感器间的耦合现象以保证模型预测精度，聚类数目不能过多。本文根据实验中机床的温度场分布特性以及传感器布置情况，将最小聚类数设置为3，即Kmin=3。最大聚类数目分以下两种情况：当温度测点n的取值范围为（3，9）时，Kmax=n；当温度测点不小于9 个时，选取个位数最大值9 与（n/4）向下取整结果中的最大值为最大聚类数目，即Kmax=max｛9，E（n/4）｝。这一方式能够对最大聚类数进行合理取值。综上，本文K的取值范围如式（4）所示。

测量实验中布置了29 个温度传感器，因此K=［3，9］。

在设置好聚类数目K值范围后，使用KMeans++算法对温度变量进行聚类，得到一系列K值对应的温度变量初始聚类中心；在此过程中，由于K-Means++聚类算法中，首个初始聚类中心为随机方式选取，因此聚类结果会受到影响。为提高聚类结果的稳定性和有效性，选取绝对平均相关系数指标最大的温度变量作为首个初始聚类中心，此温度变量与五项热误差的平均相关性在所有温度变量中最大。结合表3 可知首个初始聚类中心I1=T26。表4 为2 500 r/min 转速下聚类数目K值为［3，9］对应的温度变量聚类结果。

表4 不同K 值对应的温度变量聚类结果Tab.4 Clustering results of temperature variables corresponding to different K values

（3）根据绝对平均相关系数确定各聚类中关键温度敏感点，获取一系列温度敏感点组合。

根据表3 中温度与热误差的绝对平均相关系数计算结果，将表格4 中各K值包含的K组聚类中绝对平均相关系数最大值对应的温度变量作为该类的温度敏感点，得到不同聚类数目对应的包含相同数目温度变量的温度敏感点组合，如表5 所示，K=3 对应的3 个温度敏感点精简为T26，T25，T15，以此类推。由于T26 作为K-Means 算法的首个初始聚类中心，与五项热误差的相关性最大，表格5 中每组温度敏感点组合均包含了温度点T26。

表5 2 500 r/min转速下不同K值对应的温度敏感点组合Tab.5 Combination of temperature sensitive points corresponding to different K values at 2 500 r/min speed

为综合评估模型对五项热误差的预测性能，提高最优温度敏感点组合的通用性，建立绝对均方根差AM与绝对残差均值AS评估指标即各项热误差预测结果的均方根差平均值与残差平均值，用于评价不同温度敏感点组合对应热误差模型的预测性能。AM与AS计算公式如下：

其中：N表示预测样本总样本数量；Pi和Mi分别表示第i个样本的热误差预测值与实际测量值；S表示热误差预测值与测量值的残差均值；M表示热误差预测值与测量值的均方根差，下标对应热误差项；AS为绝对均方根差，AM表示绝对残差均值。

（5）计算评估指标，选取预测性能最优模型对应的温度敏感点组合作为最优组合。

以表5 中不同K值对应的温度敏感点作为输入，对应五项热误差为输出建立BP 神经网络对热误差进行训练和预测。其中训练集为计算绝对平均相关系数所用的某组2 500 r/min 数据的前80%数据，预测集为后20%数据。不同温度敏感点组合对应BP 热误差模型的预测性能评估指标计算结果如表6 所示。其中AS的范围为2.642～2.796 μm，AM的范围为2.677～2.855 μm，K=4 时两者最小，表示此时的热误差模型预测性能最优。为避免图像中曲线过多显得繁琐复杂，同时在保证不影响图像分析结果的前提下，文中的图像均只展示包含最优K值在内的均方根差与残差均值评估结果相差不大的部分K值对应的残差或预测曲线。图6 所示为K=3，4，5，6，7，8，9 对应的温度敏感点组合作为输入时各模型对随机选取的X2 项热误差预测的残差曲线。其中K=4 对应的残差曲线整体更接近于0，表明该曲线对应的预测效果最佳。最终选取K=4时包含的T1，T15，T25，T26 为最优温度敏感点组合。

表6 绝对残差与绝对均方根差计算结果Tab.6 Absolute residual and absolute root mean square deviation calculation results（μm）

图6 2 500 r/min 转速下不同K 值对应的X2 项热误差残差曲线Fig.6 Thermal error residual curve of X2 corresponding to different K values at 2 500 r/min

4 最优温度敏感点组合有效性验证

4.1 相同工况下不同误差项有效性验证

使用最优敏感点组合选取所用的相同工况下采集的2 500 r/min 转速数据对最优温度敏感点组合进行相同工况不同误差项的有效性验证。以表5 中不同K值对应的温度敏感点组合作为输入，建立BP 热误差模型对X1、X2、Y1、Y2 项热误差项进行预测。均方根差M与残差均值S用于评估不同温度敏感点组合对应模型的预测性能。图7（a）～7（d）分别展示了不同温度敏感点组合对应的BP 模型对X1、X2、Y1、Y2 项热误差的预测评估结果。如图所示，在对各方向热误差的预测性能评估结果中，柱形图均在K=4 时达到最低点。表明在不同温度敏感点组合中，K=4 代表的温度敏感点组合对应的热误差模型对各项热误差的预测性能最优。

图7 BP 模型对各项热误差的预测性能评估结果Fig.7 Prediction performance evaluation results of various thermal errors of BP model

表7 详细展示了图7（a）中不同温度变量组合对应的X1 项热误差的预测性能评估值计算结果。如表所示，均方根差M的最小值为0.088 μm，最大值为0.227 μm；残差均值S的最小值为0.075 μm，最大值为0.162 μm。其中M与S最小值对应的输入均为K值为4 对应的温度敏感点组合。图8 描述了K=3，4，5，6 时，对X1方向热误差的预测残差。从图中可以看出，K=4代表的残差曲线相较于其他三条曲线整体更收敛接近于0，此时的热误差模型预测性能相对更优。以上表明选取的温度敏感点组合在相同工况不同误差项中同样有效。

表7 X1 项热误差的预测性能评估结果Tab.7 Prediction performance evaluation results of thermal error of X1（μm）

图8 2 500 r/min 转速下部分K 值对应X1 项热误差预测残差Fig.8 Thermal error prediction residual of X1 corresponding to part of K values at 2 500 r/min

4.2 不同工况下同一误差项有效性验证

在机床实际加工工程中往往包含多种工况，本节验证最优温度敏感点组合在不同工况下同一热误差项中的有效性。分别以表5 中不同温度敏感点组合对应的三组不同工况下的采集数据作为输入，建立BP 热误差模型对Z向热误差进行预测。同样，均方根误差M与残差均值S用于评估不同温度敏感点组合对应模型的预测效果。

4.2.1 2 000 r/min 转速下有效性验证

首先，对2 000 r/min 转速下的热误差数据的最优温度敏感点组合进行有效性验证。按照表5中不同温度敏感点组合在2 000 r/min 转速下采集的前80%数据作为BP 模型的输入，相应的Z向热误差数据作为输出进行训练，预测后20%的Z向热误差。不同K值温度敏感点组合对应的BP 热误差模型预测性能评估结果如表8 所示。

法国强调艺术与文化教育的公平性，认为不应该让艺术与文化教育成为只是为社会中部分阶层孩子服务的“奢侈品”，而是所有孩子都能学习的基础内容之一。家庭文化艺术教育的政策应该确保所有的孩子，包括身体残疾、住院医疗，以及家庭条件差的孩子。特别是社会困难阶层的孩子，由于父母文化知识的局限，缺乏文化生活习惯，往往使其子女远离艺术文化环境。由于资源本身的平等性（如免费政策）并不能保证资源获取的平等性，法国更强调要保证100%的孩子能够“平等”地获得艺术与文化教育资源。

表8 2 000 r/min 转速下Z项热误差的不同K值评估结果Tab.8 Evaluation results of different K values of thermal error of Z at 2 000 r/min（μm）

从表8 中可以看出，在不同温度敏感点组合对应的评估结果中，M的最小值为0.149 μm，最大值为1.844 μm；S的最小值为0.122 μm，最大值为1.615 μm。其最小值对应的K值均为4。图9 展示了2 000 r/min 转速下，K=3，4，5，6，7，8，9 时对应的Z向热变形值的残差曲线。观察图9 可知，在所有残差曲线中K=4 的对应的残差曲线整体更加平缓与收敛，预测结果相对于其他曲线更优，表明最优温度敏感点组合在2 000 r/min转速热误差数据有效性良好。

图9 2 000 r/min 转速下不同温度敏感点组合对应Z 项热误差预测结果Fig.9 Thermal error prediction result of Z corresponding to the combination of different temperature sensitive points at 2 000 r/min

4.2.2 3 000 r/min 转速下最优温度敏感点组合有效性验证

同样，使用3 000 r/min 转速下采集的实验数据，以不同温度敏感点组合数据为输入，对应的Z向热误差数据为输出建立BP 模型，验证最优K值温度敏感点组合的有效性。数据的前80%用于训练，后20%用于预测。不同K值温度敏感点组合对应的BP 神经网络热误差模型的预测评估结果如表9 所示。分析表9 内容可知，在不同K值温度变量组合对应的热误差模型预测性能评估结果中，评估值M与S在K=4 处最低，分别为0.129 μm 与0.107 μm；在K=8 处最高，分别为0.268 μm 与0.247 μm。同时，图10 展示了K=3，4，5，6 对应的BP 模型的预测残差曲线。如图所示，K=4 代表的残差曲线整体更靠近零，表明此时对应的热误差模型的总体预测性能相对最优。最优温度敏感点组合在3 000 r/min 转速下采集的数据中同样适用。

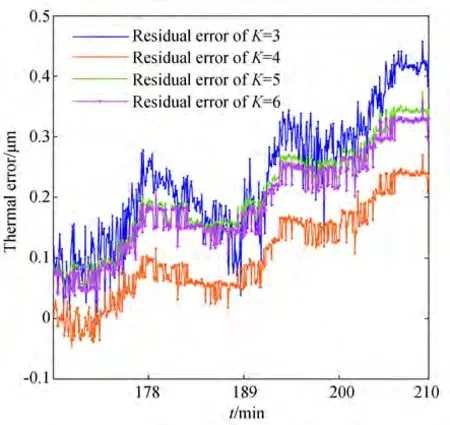
图10 3 000 r/min 转速下部分温度敏感点组合对应Z 项热误差的预测残差Fig.10 Prediction residual of thermal error of Z corresponding to part temperature sensitive points combination at 3 000 r/min

表9 3 000 r/min 转速Z 向热误差不同K 值评估结果Tab.9 Evaluation results of different K values of Z directions at 3 000 r/min（μm）

4.2.3 5 000 r/min 转速下最优温度敏感点组合有效性验证

验证最优温度敏感点组合在5 000 r/min 转速下的有效性。本组数据的采集样本数为2 334，采集时间约为3.2 h。以不同K值温度敏感点组合对应的温度数据作为输入，Z向热误差作为输出建立BP 热误差模型。数据的前80%作为训练集，后20%作为测试集。5 000 r/min 转速下不同K值对应的Z向热误差预测结果评估结果如表10 所示。其中均方根差M的最小值为0.157 μm，残差均值的最小值为0.137 μm，对应的K值均为4。图11 为不同K值对应的BP 神经网络预测Z向热误差的残差曲线。从图中可以看出，K=3 与K=4 对应的残差曲线整体更接近于0，预测效果较其他组合更优。结合表10 中的评估指标与图10 中不同温度敏感点组合对应的残差曲线，可知K=4 对应的温度敏感点组合预测效果最优。最优温度敏感点组合在5 000 r/min 转速下仍然有效。

图11 5 000 r/min 转速不同温度敏感点组合对应Z 项热误差预测残差Fig.11 Prediction residual of part temperature sensitive point combination corresponding to thermal error of Z at 5 000 r/min

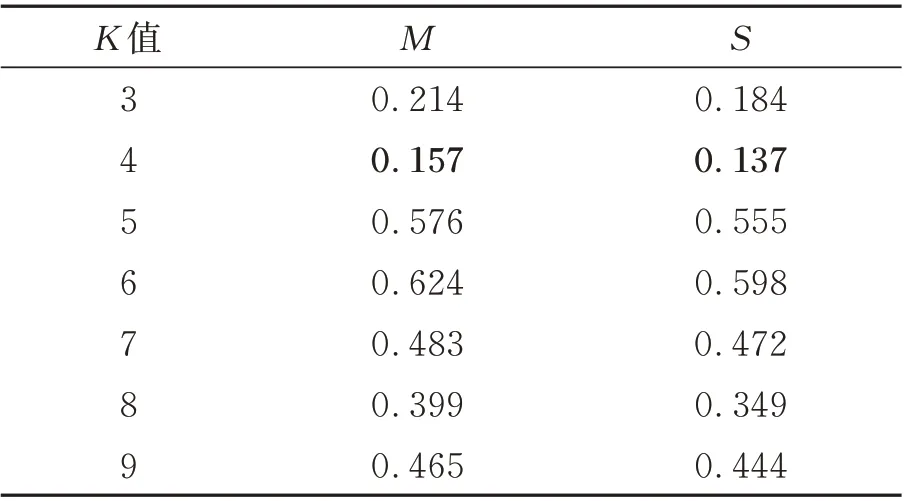
表10 5 000 r/min 转速下Z 项热误差不同K 值评估结果Tab.10 Evaluation results of different K values of thermal error of Z at 5 000 r/min（μm）

综上所述，使用由本文提出的最优温度敏感点综合选取法在2 500 r/min 工况下选取的最优温度敏感点组合在相同工况下不同误差项以及不同工况下同一误差项中同样有效。

5 最优温度敏感点组合通用性验证

验证最优温度敏感点组合在不同热误差模型中的通用性。使用2 500 r/min 转速下采集的数据，以表格5 中不同K值对应的温度敏感点组合作为输入，以变化最明显的Z方向的热误差数据作为输出，分别建立RBF 神经网络、SVM 模型与MLR 热误差模型。数据的前80%用于模型的训练，后20%用于预测。均方根误差M与残差均值S用于评估不同温度敏感点组合对应的热误差模型对Z向热误差的预测效果。为更方便地对比以及分析不同温度敏感点组合对应模型的预测效果，图12～14 仅呈现了K=4，5，6，7 对应的部分残差曲线或预测值曲线，由于其它K值的均方根误差与残差均值评估结果与这四组结果相差较大，故不在图中呈现。

图12 2 500 r/min 转速下部分温度敏感点组合对应RBF 模型的Z 项热误差预测结果Fig.12 Thermal error predictive results of thermal error of Z of RBF model corresponding to part of sensitive temperature points at 2 500 r/min

图12（a）展示了K=4，5，6，7 对应的RBF 模型对Z向热误差的预测结果，其中K=4 对应的Z向热误差预测曲线与实验测量曲线整体更为接近；图12（b）为图12（a）中预测结果对应的残差曲线，其中K=4 对应的残差曲线相对于其余三条曲线整体更靠近0。表11 所示为不同K值温度敏感点组合作为输入对应的RBF 模型预测性能评估结果，其中M与S的最小值分别为0.357 μm 与0.323 μm，对应的K值为4；最大值分别为1.824 μm 与1.625 μm，对应的K值为3。结合图12 与表11 可以看出K=4 代表的温度敏感点组合对应的RBF 热误差模型预测效果最佳。

表11 2 500 r/min 转速下不同K 值对应RBF 模型预测性能评估结果Tab.11 Evaluation results of RBF model prediction performance corresponding to different K values at 2 500 r/min（μm）

表12 与图13，表13 与图14 分别展示了不同K值对应的温度敏感点组合作为输入时SVM 与MLR 热误差模型的评估结果。同理分析，K=4对应的M与S在不同的热误差模型中均为最小，对应的模型预测性能仍为最优。表明本文选取的最优温度敏感点组合对热误差模型的依赖性较弱，在不同的热误差模型中具有良好的通用性。

图13 2 500 r/min 转速下部分温度敏感点组合对应SVM 模型的Z 项热误差预测结果Fig.13 Thermal error predictive results of thermal error of Z of SVM model corresponding to part of sensitive temperature points at 2 500 r/min

图14 2 500 r/min 转速下部分温度敏感点组合对应MLR 热误差模型Z 项热误差预测结果Fig.14 Thermal error predictive results of thermal error of Z of MLR model corresponding to part of sensitive temperature points at 2 500 r/min

表12 2 500 r/min 转速下不同K 值对应SVM 模型预测性能评估结果Tab.12 Evaluation results of SVM model prediction performance corresponding to different K values at 2 500 r/min（μm）

表13 2 500 r/min 转速下不同K 值对应MLR 模型预测性能评估结果Tab.13 Evaluation results of SVM model prediction performance corresponding to different K values at 2 500 r/min（μm）

6 结 论

本文提出了一种数量自动确定的热误差通用型温度敏感点组合选取方法。所选择的最优敏感点组合适用于不同工况下的热误差预测且对模型的依赖性不大，在不同热误差模型中的通用性良好。

首先，计算各温度变量与五项热误差之间的绝对均相关系数。其次，选取绝对均相关系数最大的温度点作为K-Means++算法的首个初始聚类中心并设置K值的范围对各温度变量进行聚类。选择各聚类中绝对相关系数最大的关键温度变量，得到对应不同聚类数目的温度敏感点组合。然后，建立BP 神经网络热误差模型，并提出绝对均方根误差与绝对残差均值评估指标来获取预测性能最优的温度敏感点组合。

最后，在VMC850 数控机床上对本文所提的方法进行验证。通过对不同工况相同误差项和相同工况不同误差项的预测验证了最优温度敏感点组合的有效性；通过建立三种热误差模型验证了最优温度敏感点组合在不同热误差模型中的通用性。