考虑道路抢修和负荷恢复的电动汽车分层调度策略

苏 粟，韦存昊，陈奇芳，李泽宁，夏明超

（北京交通大学电气工程学院，北京市 100044）

0 引言

近年来，极端灾害（如地震、台风、洪水等）造成的停电事故屡有发生［1-2］，对人身及财产安全造成了巨大损失［3］。因此，研究者们十分关注如何在灾后快速地恢复重要负荷并尽量延长其供电时间，从而提高灾后配电网的韧性［4］。

“双碳”目标使得电动汽车（electric vehicle，EV）的数量快速增长［5］，也为负荷恢复提供了新的思路。配置大量闲置且利用率低的分布式电源（distributed generator，DG）必然会造成资源浪费和成本过高［6］。而EV 可视为能灵活调配的供电资源，能根据配电网的需要进行统一控制与调度［7］。因此，在紧急情况下调度EV 为重要负荷供电是一种经济且灵活的负荷恢复方法［8-9］。

在上述背景下，本文聚焦于如何在极端灾害后合理地利用EV 参与负荷恢复服务。文献［10-13］合理利用了闲置的EV 能量恢复电力负荷。但上述文献仅将EV 视为供电源，交通网和配电网的耦合涉及较少。而EV 作为配电网和交通网的耦合点，不仅需要考虑其源荷特性，还需要考虑其在交通网内的空间行为特性［14］。文献［15-16］聚焦于EV 的空间调度，求解EV 能量在各充放电站的最优配置方案，但文献［15］仅采用配电网拓扑而非具体的交通网研究路径规划，忽略了很多实际因素，文献［16］没有讨论EV 能量在时间尺度上的优化利用。文献［17］中电动公交的目的地是固定的，没有通过策略来确定各电动公交的最优放电站点，因此无法充分发挥电动公交的地理灵活性。

此外，极端灾害往往伴随着对电网元件或交通道路的破坏。文献［18-21］均涉及了电网维修人员的修复次序及修复路径的协同规划，以此提升恢复效果，但文献［18］没有考虑配电网和实际交通路网的耦合，文献［19］没有考虑极端情况下可用能源的有限性，其DG 被视为故障周期内能量相对充足的供电源，文献［20-21］中人员在故障点间的行驶时间分别为随机生成和仅以距离参数衡量，缺乏完善的路径规划模型。上述文献除了前文所提的局限外，都只聚焦于各故障元件的维修顺序问题，没有在实际路网中讨论路径规划问题，忽略了不同路段的通行速度差异，也没有考虑交通道路的损坏或供电EV 的行驶能耗对负荷恢复的影响。

极端灾害后，部分道路会因为地面塌陷、树木倒伏等情况影响车辆的通行。为了减小对社会的影响，道路抢修队会优先对重要损坏道路进行紧急抢修。因此，EV 的路径规划也需要充分考虑损坏道路和道路抢修产生的影响。文献［22］简单考虑了实际路网中某条道路损坏后的电网维修队与供电EV 的调配问题，但没有引入对损坏道路的抢修，供电EV 停下并等待抢修完成或选择绕路的决策问题也就没有得到充分的探讨，道路抢修对负荷恢复的辅助作用没有得到深入研究。上述文献对本文道路抢修队调配问题的建模提供了一定的参考价值，但仍与本文研究具有本质区别。在国内的灾后应急响应机制下，考虑各政府救灾部门之间的行动影响具有一定的现实意义。

针对上述研究内容，本文所提策略考虑了道路的损坏及抢修对电动汽车路径的影响，并对道路抢修队和电动汽车在交通网内的行动轨迹进行了统筹优化。同时，基于配电网与交通网的耦合，充分发挥了电动汽车能量在时空尺度上的灵活性优势，进而提升停电期间的负荷恢复效果。

1 城市道路抢修辅助重要负荷恢复的框架与建模

1.1 计及道路抢修的重要负荷恢复框架

计及道路抢修辅助作用的两网耦合恢复框架如图1 所示，主要分为交通层和电网层。由于电动汽车既具有交通属性，也具备电气特性［23］，因此，充放电站被视为交通层和电网层的耦合点。本文具体采用电动公交进行分析，因为其具有电池容量大、利于负荷恢复、方便统一调度的优点。

图1 计及道路抢修的重要负荷恢复框架Fig.1 Framework of critical load restoration considering road repair

基于该框架，本文提出了一种电动汽车能量时空调度策略。首先，灾后能量管理系统（postdisaster energy management system，PDEMS）收集配电网的故障情况，并从交通部门获取道路损坏状况和道路通行速度等数据信息［24］，通过评估灾害的影响程度和范围，对配电网恢复主网供电的时间进行预测。然后，PDEMS 统筹规划网内可用供电资源和待恢复的负荷需求，合理决策各电动公交的目标站点，同时协调道路抢修队的抢修行动进行配合。电动公交到站后通过电动汽车与电网互动（vehicle-to-grid，V2G）技术进行供电服务。有限供电资源采用多时段协同的多源供电方式，尽可能地延长较重要负荷的持续供电时间。

1.2 道路抢修队模型

每支道路抢修队的第1 个起讫点（origindestination，O-D）对均为从道路抢修站到第1 条抢修道路，最后一个O-D 对是从最后一条抢修道路返回道路抢修站，各O-D 对均以行驶时间最短为目标分别进行规划。任一O-D 对的行驶模型可表示为：

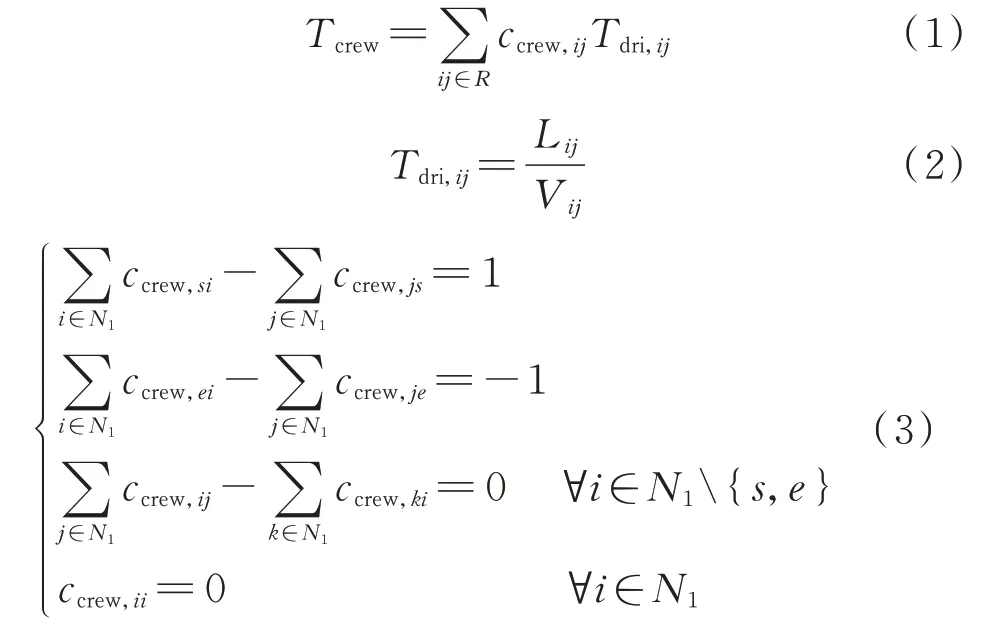
式中：R和N1分别为交通路网中的道路集合和节点集合；Tcrew为道路抢修队以出发点s、目的地点e为O-D 对的行驶总时间；Tdri，ij、Lij、Vij分别为道路ij的行驶时间、道路长度和通行速度；ccrew，ij为该抢修队的行驶路径是否经过道路ij的布尔变量，取值为1表示该抢修队经过道路ij，取值为0 表示该抢修队不经过道路ij；ccrew，ii为抢修队是否停留在节点i的布尔变量，取值为1 表示抢修队停留在节点i，取值为0 表示抢修队不停留在节点i；下标k表示节点。式（3）保证了所求路径是以s点为起点、e点为终点的连通路径。

式（4）至式（7）为道路维修队整个维修工作周期内的行动轨迹模型。

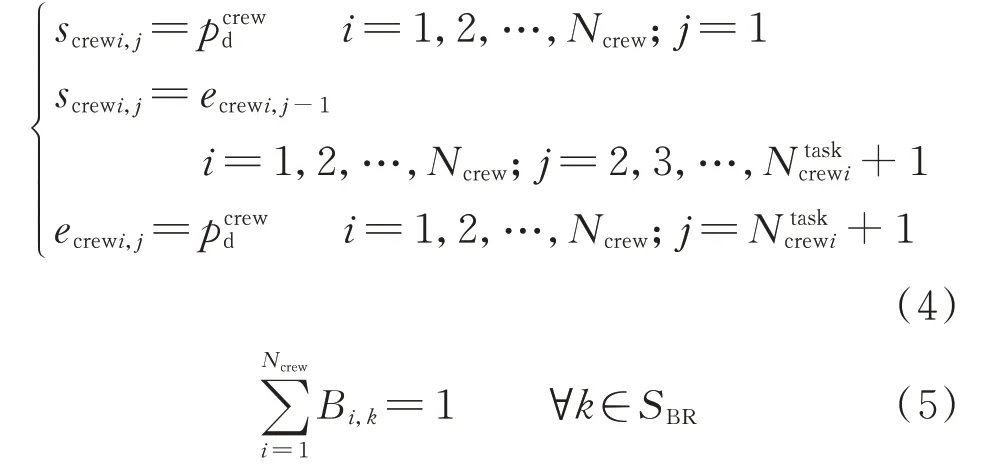
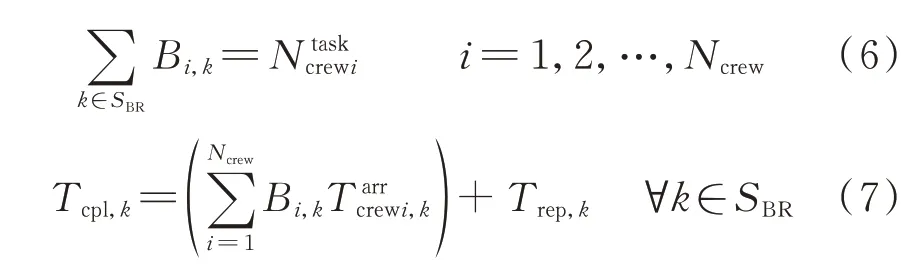
1.3 电动公交模型

在所提策略中，每辆电动公交只有一个O-D对，出发点s均为电动公交场站，目的地点e为策略所分配的充放电站点。

电动公交通过路段ij的总时间Tij如式（8）所示，此处的路段ij行驶时间Tdri，ij与道路抢修队中的定义相同，但在总通行时间中引入了等待时间Twait，ij。

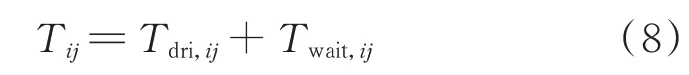
特定速度下路段ij的电动汽车能耗Econs，ij如式（9）所示［25］，其对负荷恢复效果的影响在1.4.3 节进行说明。

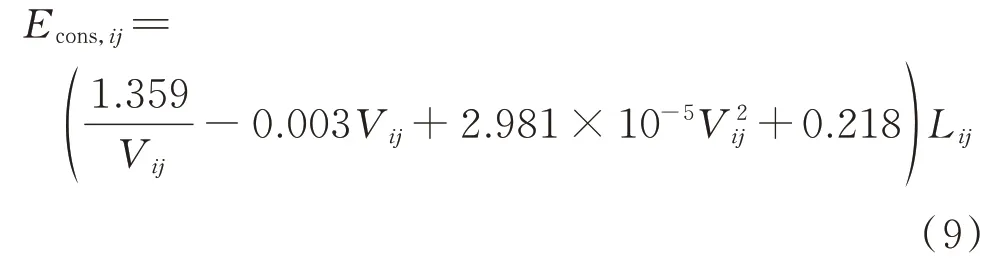
电动公交经过某道路时停下等待的时间如式（10）所示。

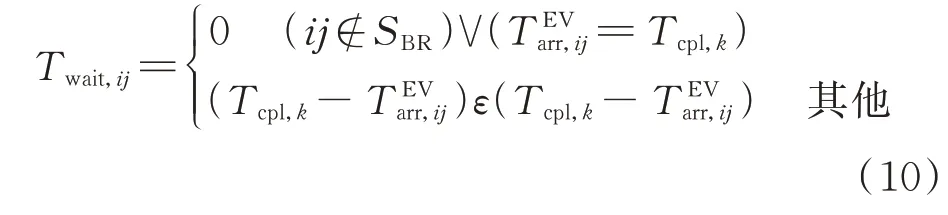
式中：ε(·)为单位阶跃函数；TEVarr，ij为电动公交到达损坏道路ij的时间，此处定义到达道路两端的任一节点即为到达该道路。非损坏路段或已抢修完成的损坏路段的等待时间为0。因此，道路抢修队和电动公交到达损坏道路的先后顺序及时间差对其行为决策具有一定的影响。

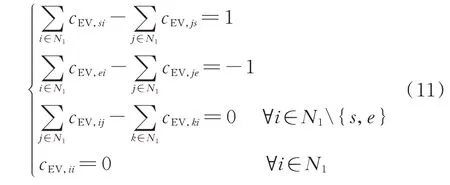
式中：cEV，ij为电动公交的行驶路径是否经过道路ij的布尔变量；cEV，ii为电动公交是否停留在节点i的布尔变量。式（11）保证了求解出来的电动公交的行驶路径是以s点为起点、e点为终点的连通路径。

1.4 多时段协同负荷恢复模型

本文采用支路潮流模型（branch flow model，BFM）分析配电网侧具体的负荷恢复细节。

1.4.1 配电网的辐射状拓扑

根据辐射状网络的充要条件［26］，建立如下所示的配电网拓扑模型。

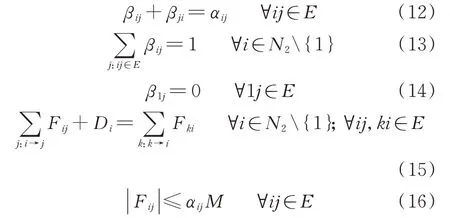
式中：E和N2分别为配电网中支路和节点的集合；j：ij表示能与节点i构成支路的所有节点；j：i→j表示节点i所有的下游节点j；βij和αij分别为支路连通状态的布尔变量和节点间父子关系的布尔变量，βij=1 表示支路ij连通，βji=0 且αij=βij=βji=0表示节点i为节点j的子节点；Fij为支路ij的虚拟潮流；Di为节点i的虚拟负荷；M为值很大的正实数。式（12）描述了支路连通状态和节点父子关系变量之间的关系；式（13）至式（15）表示除根节点外的其他节点均只有一个父节点，且能保证虚拟潮流的平衡；式（16）保证了若支路ij不连通，其虚拟潮流为0。

1.4.2 配电网的运行潮流方程

基于BFM 的配电网运行数学模型由以下潮流方程描述。

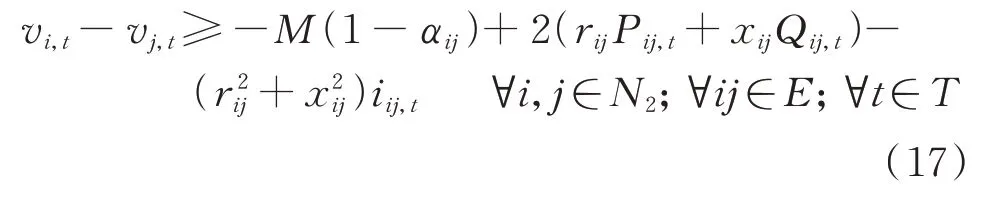
式中：T为停电周期内的时段集合；vi，t为节点i在t时段的电压幅值的平方；iij，t为支路ij在t时段的电流幅值的平方；Pij，t和Qij，t分别为支路ij在t时段的有功和无功功率；rij和xij分别为支路ij的电阻和电抗。式（17）和式（18）描述了2 个节点电压之间的平方差关系。式中：Shi，t为支路hi在t时段的复功率；zhi为支路hi的阻抗；s、s和si，t分别为节点i在t时段的出力复功率、负荷复功率和注入配电网的复功率；γi，t为节点i在t时段的负荷状态，若该节点的负荷得以恢复，其值为1，否则为0。式（19）保证了每个节点的复功率平衡，而式（20）为节点注入复功率的计算公式。

式（21）给出了电压、电流和功率之间的关系，而式（22）为t时刻系统网损Ploss，t的计算公式。

由于式（19）为一个含布尔变量的非线性方程，需要通过分段线性化方法转化为线性约束后再进行求解。通过添加如下约束，式（19）中的3 个非线性项分别转化为了λij，t、λhi，t和yhi，t这3 个线性项。

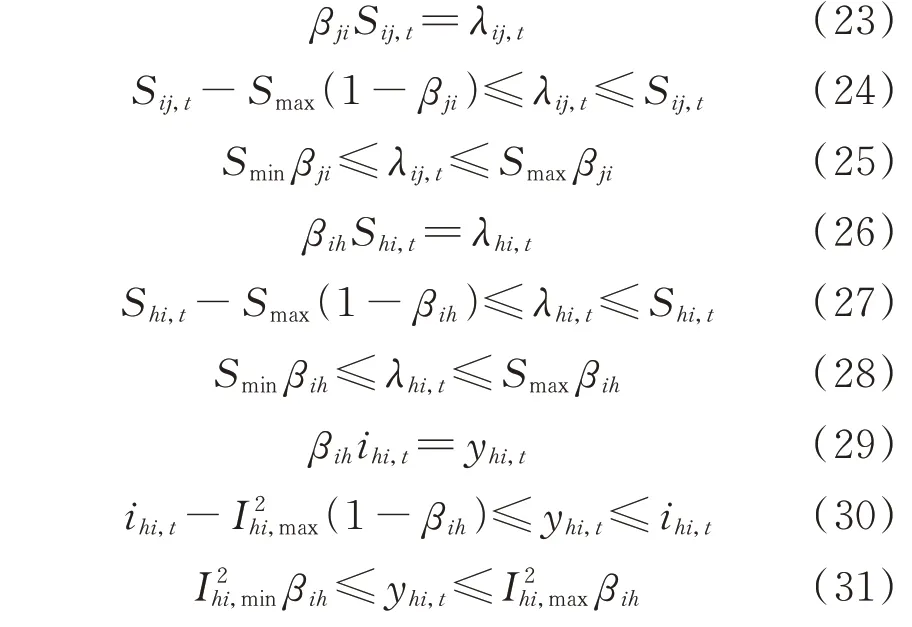
式中：Smax、Smin和Ihi，max、Ihi，min分别为对应支路所允许的复功率上、下限和电流幅值上、下限。重复使用该方法，可以将整个模型内其他含布尔变量的类似非线性项均转化为线性项，以保证所建立模型的可求解性。

式（21）为一个不含布尔变量的非凸非线性约束，也需要采用特定的方法对其进行转化。通过二阶锥松弛（second-order conic relaxation，SOCR）法，式（21）将被转化为：

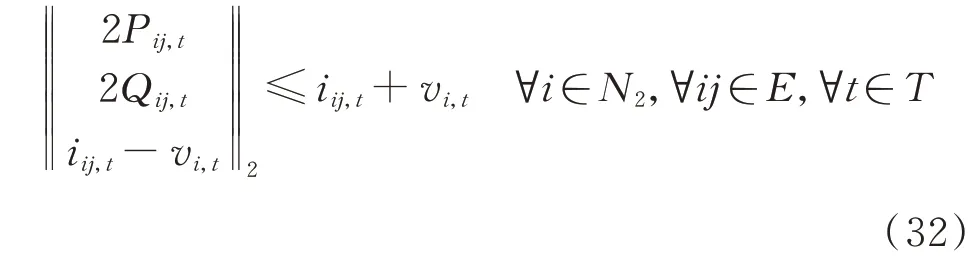
文献［27］证明了在BFM 中采用SOCR 法松弛电力系统潮流方程足以满足精确度要求。因此，原问题已被转化为混合整数二阶锥规划问题，从而简化了求解过程。具体的SOCR 误差分析将在3.2.1节展示，以此验证所建立模型的优化准确性。松弛后支路ij在t时段的偏差Δ为：

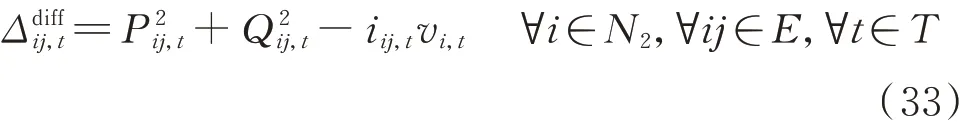
1.4.3 各供电源的能量限制

用于紧急情况负荷恢复的分布式发电机多为柴油机或燃气轮机，其可用能量取决于储备的柴油或燃气量。式（34）限制了分布式发电机的出力之和不能超过其能量储备。

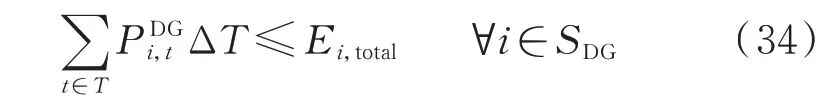
式中：SDG为含分布式发电机的配电网节点集合；P和Ei，total分别为分布式发电机节点i在t时段的出力及其储备能量；ΔT为每个时段的时长。

而电动汽车充放电站的可用能量则取决于其站内的电动公交数量及其剩余荷电状态（state of charge，SOC）。

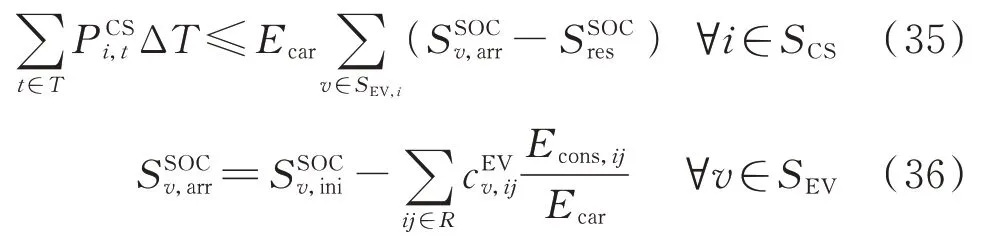
式中：SCS为含充放电站的配电网节点集合；SEV和SEV，i分别为所有电动公交集合和前往位于节点i的充放电站的电动公交集合；P为电动汽车充放电站节点i在t时段的出力；Ecar为电动公交的电池容量；分别为电动公交v的初始SOC、到达指定充放电站时的SOC 和需要为电动公交预留的SOC；c为电动公交v是否经过路段ij的布尔变量，取值为1 表示经过。式（35）描述了集成电动公交的充放电站的供电能力；式（36）表示电动公交到达指定充放电站时的SOC 等于其初始SOC 减去行驶途中的能耗。式（35）和式（36）体现了电动公交的行驶能耗对负荷恢复产生的影响。

为了保证用户具有良好的用电体验，此处要求一旦某节点的负荷得到恢复，将不能被再次切断，具体的约束可表示为：

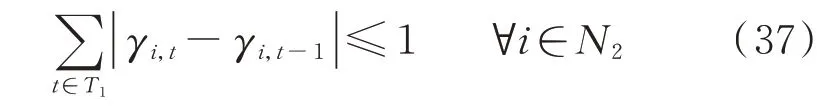
式中：T1为除去第1 时段后的停电周期时段集合。

2 城市道路抢修辅助重要负荷恢复的电动汽车能量时空分层调度方法

2.1 目标函数

2.1.1 确定能量在空间尺度上的优化配置

重要负荷恢复策略的主要目的是在停电过程中尽可能延长更多的重要负荷的供电时间。第1 阶段以此为优化目标，在假设路网中没有损坏道路的情况下，同时考虑电动公交路径规划模型和多时段协同负荷恢复模型，确定电动公交的优化分配结果，目标函数可表示为：

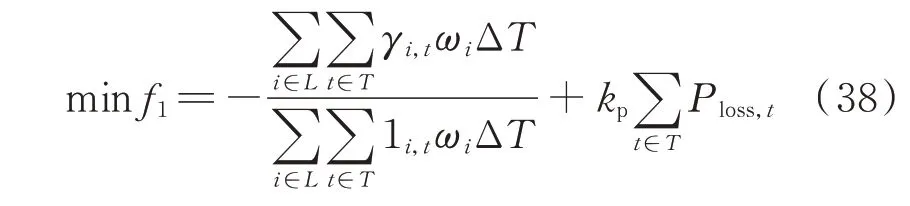
式中：L为含有重要负荷的配电网节点集合；ωi为节点i的负荷权重系数，表征其重要程度；1i，t表示节点i在t时段的负荷状态为1，即已被恢复；kp为惩罚系数。该目标函数的第1 项考虑了各节点负荷的重要程度，旨在最大化故障配电网的加权负荷供电时间；第2 项为系统总网损的惩罚项，为保证SOCR 的准确性而引入［28］。由于恢复重要负荷才是本策略的主要目标，惩罚系数kp的取值应较小。

2.1.2 确定道路抢修队和电动公交的行动轨迹

第2 阶段考虑道路损坏的情况以及第1 阶段求解的电动公交分配结果，协调道路抢修队的行动来配合电动公交，以最小化所有电动公交前往充放电站的时间、距离之和为主要目标，确定损坏道路的抢修顺序、抢修队与电动公交的行驶路径，并输出电动公交到达充放电站的时间与剩余SOC，具体的目标函数可表示为：

1.在构建安居乐业、文明祥和的社会生活共同体上，社会环境更加和美幸福。加快形成“社会安全”得以全面维护的“平安”环境，即社会矛盾得以化解，社会冲突得以调适，社会正义得以伸张，社会公平得以体现，社会富裕得以保障，社会和美得以实现，使以“安定”为基本目标的“治安”、“稳定”转向以“安康”为目标的“平安”、“和美”。

式中：Lbase和Tbase分别为行驶距离和行驶时间的基底，分别等于路网所有道路的长度之和以及行驶时间之和；NCS为电动汽车充放电站的数量；N为分配至第m个充放电站的电动公交数量，由第1 阶段求解得出；cEVm，ij为前往第m个充放电站电动公交车队是否经过道路ij的布尔变量，取值为1 表示经过；q表示损坏道路；σ为权重系数。此处将前往同一充放电站的若干电动公交统一视为一个车队，因为其具有相同的起讫点和行驶路径。该目标函数旨在通过决策道路抢修队的抢修顺序和路径来实现电动公交行驶路径的优化。而在该目标函数中引入所有道路抢修完成的时间（即目标函数的第2 项）是为了在保证电动公交的行驶时间、距离之和取最小值且具有多个抢修顺序和路径的最优解的情况下，求解出一组能最快抢修完成所有道路的最优解，因此，权重系数σ取值应较小，避免影响主要的优化目标。

2.1.3 确定能量在时间尺度上的优化配置

本阶段综合考虑上一阶段输出的可用资源总量和各供电源可以开始供电的时间，以及待恢复负荷的权重和功率，仍以最大化加权负荷供电时间为主要目标，统筹规划每个时段的各供电源出力，并确定各时段得以恢复供电的重要负荷，具体的目标函数可表示为：

上述分层调度方法实现了电动汽车能量在时空尺度上的优化配置，也实现了道路抢修队辅助性协助作用的有效利用，为本文负荷恢复策略所具有的优越性提供了基础。

2.2 约束条件

式（41）和式（42）将电压和电流幅值限制在允许的范围内。

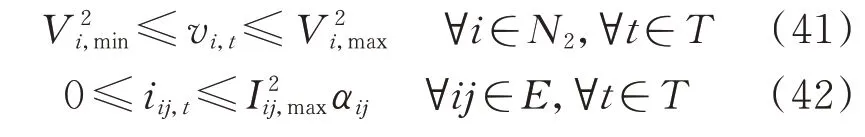
式中：Vi，max和Vi，min分别为节点i的电压幅值上、下限；Iij，max为支路ij所允许的电流幅值最大值。

式（43）说明了若支路ih没有连通，该支路的复功率为0。

式（44）限制了分布式发电机节点的输出功率。

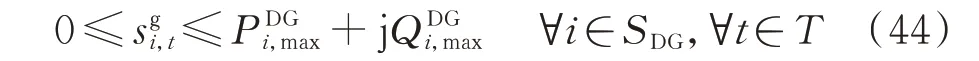
式中：P和Q分别为位于配电节点i的分布式发电机的有功出力最大值和无功出力最大值。

式（45）说明了充放电站的输出功率受其电动公交数量的影响。

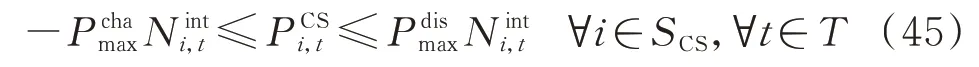
式中：P和P分别为每辆电动公交充、放电功率的最大值；N为充放电站配电节点i在t时段所接入的电动公交数量。

综上所述，该模型第1 阶段以式（38）为优化目标，式（8）至式（20）、式（22）至式（32）、式（34）至式（37）、式（41）至式（45）为约束条件，确定各充放电站分配到的电动公交数量；第2 阶段以式（39）为优化目标，式（1）至式（11）为约束条件，确定各电动公交车队到达指定充放电站的时间和剩余SOC；第3 阶段以式（40）为优化目标，式（12）至式（20）、式（22）至式（32）、式（34）至式（37）、式（41）至式（45）为约束条件，输出各时段的各供电源出力和负荷恢复情况。

2.3 求解流程

通过在MATLAB-Yalmip 仿真平台上调用Gurobi 工具箱对前文所建立的模型进行求解。仿真环境的操作系统为Win10 64 bit，硬件环境为Intel i7-9700HQ CPU 3.00 GHz，16 GB RAM，所用版本为MATLAB R2016b。

本文模型的求解流程如附录A 图A1 所示，具体的步骤见附录A。

3 仿真与算例分析

3.1 场景设定

本节算例所基于的配电网和城市交通路网的拓扑及相关说明见附录B［29-30］。电动公交的最大充放电功率为100 kW，电池容量为135 kW·h，初始SOC和预留SOC 分别为0.9 p.u.和0.2 p.u.。假设对灾害的影响范围和程度进行评估后得知，2 h 后才能清除所有配电线路的故障并恢复主网对配电网的供电。每一时段的时长ΔT设为4 min，共有30 个时段。

3.2 结果分析与讨论

3.2.1 场景1 下不同策略的调度结果

本节将对3 种不同策略（S1、S2、S3）的调度结果进行对比分析，以验证本文所提策略的有效性与优越性。3 种策略的详细说明见附录B，其具体差异如表1 所示。

表1 3 种策略间的差异Table 1 Differences among three strategies

在该故障场景下，3 种策略的开关动作如附录B图B4 所示。为了进一步对比3 种策略的调度效果，本节将被恢复负荷的加权数量NW作为衡量重要负荷恢复效果的指标：

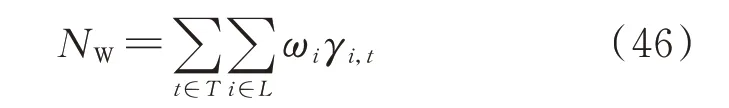
S1、S2、S3 的NW分别为9 233.2、9 500.0、9 520.6。可见S3 的负荷恢复效果最优，S1 的负荷恢复效果最差，因为各充放电站的最大输出功率与可用能量均取决于其电动公交数量。而S1 和S2 没有对有限的电动公交数量进行优化分配，电动公交被平均分配至3 个充放电站，因此，这2 个策略中的充放电站点无法得到最优的功率和能量配置，电动公交的能量没有得到空间上的优化调度，导致其负荷恢复效果较S3 而言有所下降。S1 还采用了单时间断面的负荷恢复策略，使得其负荷恢复效果在S2的基础上进一步下降。单时间断面的负荷恢复策略并未考虑能量在时间尺度上的优化配置，每一时段都恢复尽可能多的重要负荷，不具备对有限能量进行合理留存的能力。

图2 展示了每一时段被恢复的重要负荷的数量和总功率，不同颜色的柱形代表着不同等级的重要负荷，且不互相遮挡。

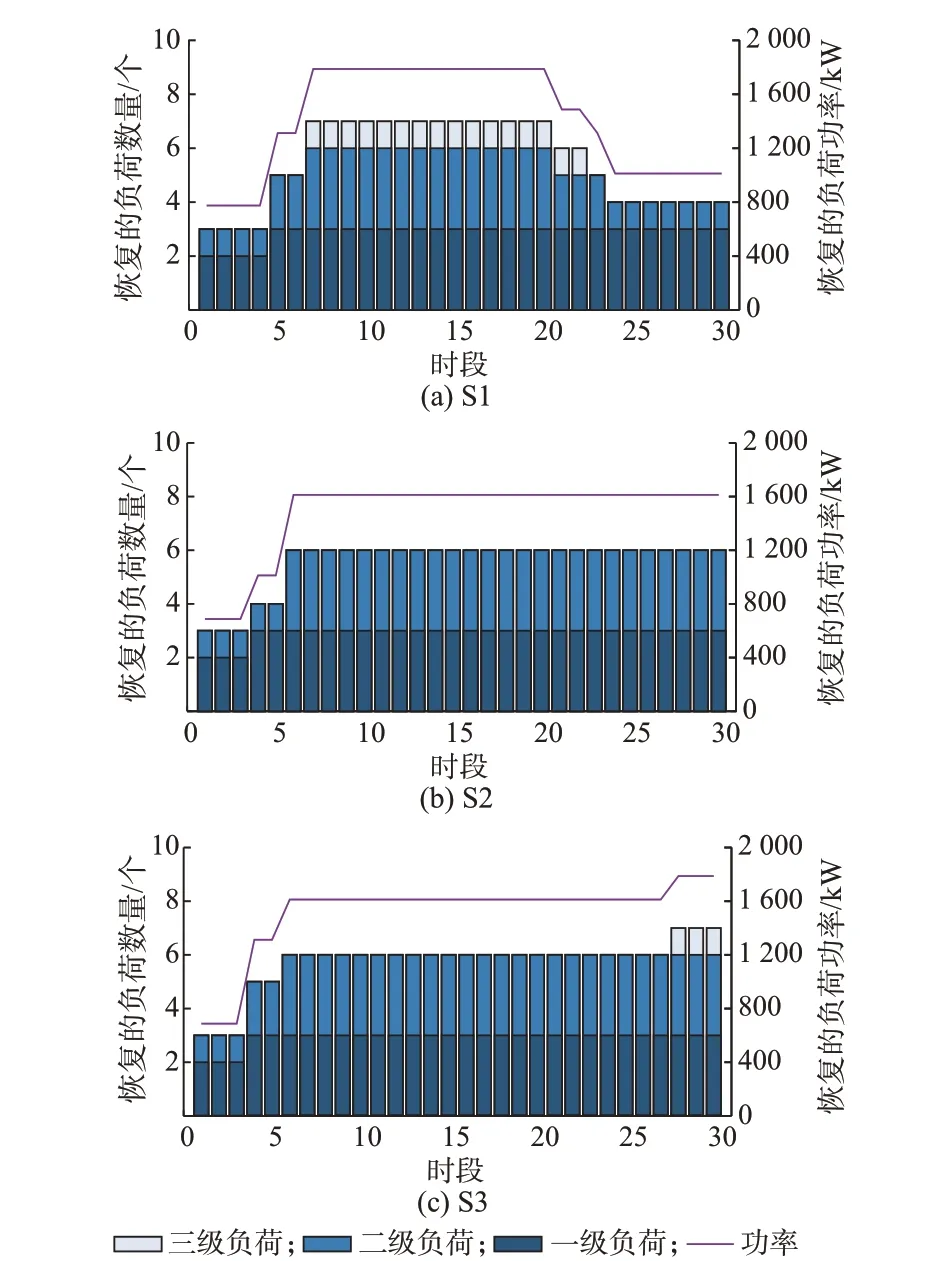
图2 重要负荷的恢复情况（场景1）Fig.2 Restoration situation of critical loads（scenario 1）

以图2（a）为例，在第15 时段共有3 个一级负荷、3 个二级负荷和1 个三级负荷得以恢复。从图2（a）可以看出，随着电动公交逐渐到达各充放电站，大部分的重要负荷均得到了恢复。但由于S1 的单时间断面负荷恢复策略，其部分充放电站的能量被过快地消耗，导致后几个时段无法支撑全部的二级负荷，因此S1 的NW较小。从图2（b）、（c）可以看出，电动公交逐渐到达充放电站后，一级和二级负荷可以持续地得到能量供应直至停电结束，这是因为S2 和S3 采用的多时段协同负荷恢复策略可以较好地规划能量的使用，从而延长权重较大负荷的持续供电时间。与S2 相比，更多的二、三级负荷在S3 中得到恢复，因为其电动公交的地理灵活性得到了充分的发挥，从而提升了负荷恢复的效果。图2 同时还展示了每一时段被恢复负荷的总功率，S1 的功率曲线因为能量的消耗在后期有所下降，部分负荷出现了恢复供电后又被切断的情况，对用户的用电体验产生了不良的影响。而S2 和S3 的功率曲线随着电动公交的到站而升高，并在调度后期保持着相对稳定。

附录B 图B5 展示了S3 中所有节点的电压均可时刻保持在0.95 p.u.以上，在一定程度上支撑了所提策略的可行性。S3 的误差散点图如图B6 所示，可知各支路的误差均小于10-7，验证了本文模型的准确性以及仿真结果的可靠性。

道路抢修队与电动公交的最优行驶路径如图3所示。图中：Crew1 和Crew2 表示2 支道路维修队；EV1、EV2、EV3 表示3 支电动公交车队，这里将前往同一充放电站的电动公交视为一支车队；CS1：7表示充电站CS1 分配到7 辆电动公交，CS2：10 表示充电站CS2 分配到10 辆电动公交，CS3：1 表示充电站CS3 分配到1 辆电动公交。对道路抢修队进行路径规划可以提前其到达损坏路段的时间，使损坏路段更早地得到修复。而对电动公交进行路径规划可以在行驶路径受损坏道路影响的情况下替每支车队决策是选择绕路还是选择等待道路抢修完成，使其以较短的行驶时间和能耗到达指定的充放电站，以此协助重要负荷的恢复。

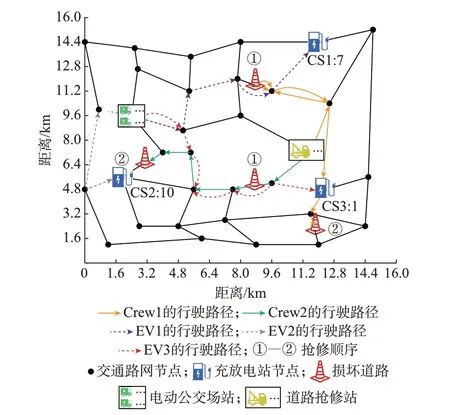
图3 S3 中道路抢修队和电动公交的最优路径(场景1)Fig.3 Optimal routes of road repair crews and electric buses in S3 (scenario 1)

如图4 和附录B 表B1 所示，2 支抢修队均优先抢修了电动公交需要经过的损坏路段，其中没有选择优先抢修道路B2 是因为B2 离道路抢修站较远，抢修队需要花费较长时间赶到B2，但电动公交场站离CS2 较近，选择绕路比等待抢修花费的额外行驶成本更少。因此，2 支抢修队优先保障EV1 和EV3的通行。EV1 到达损坏路段B1 的时间与该道路抢修完成的时间较为接近，因此选择原地等待B1 道路抢修完成，再继续行驶。EV2 需要经过的道路B2 抢修顺序靠后，因此选择绕路前往CS2。而EV3 到达道路B3 时，该道路的抢修工作已经完成，EV3 无须等待即可顺利通行。而损坏道路对电动公交的行驶路径造成的具体影响如表2 所示，由于道路的损坏，电动公交的行驶时间和能耗均会受到不利影响。但本文所提策略为电动公交合理地决策了绕路和等待行为，尽可能地降低了道路损坏对电动公交通行造成的不利影响。

表2 S3 中电动公交行驶情况(场景1)Table 2 Traveling situation of electric buses in S3 (scenario 1)

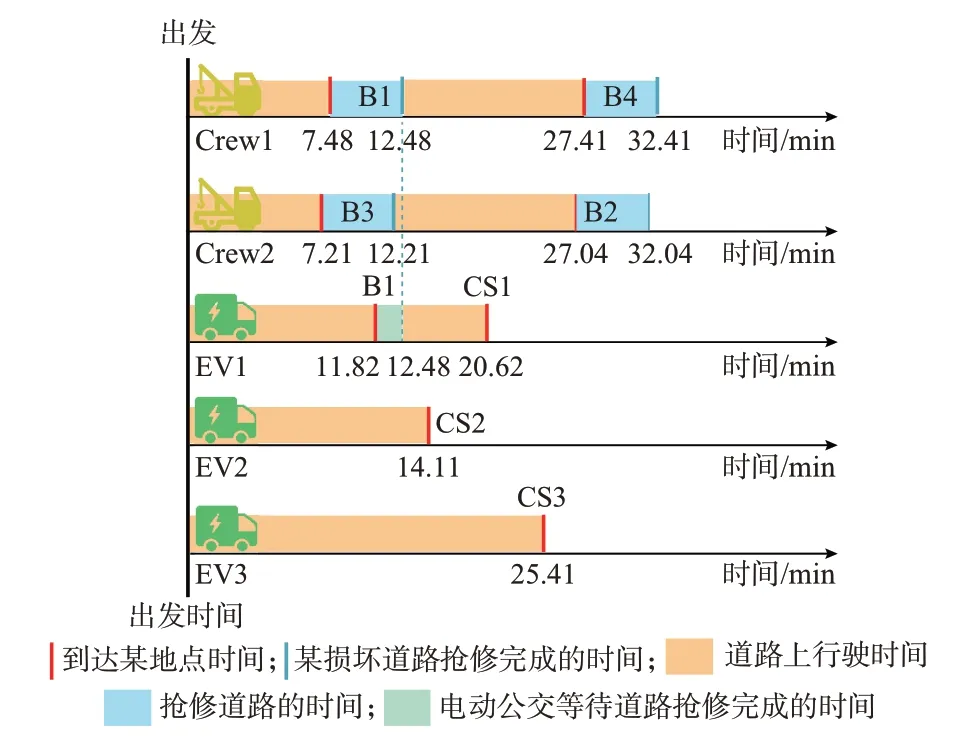
图4 S3 中道路抢修队和电动公交的行动时序图(场景1)Fig.4 Action sequence diagram of road repair crews and electric buses in S3 (scenario 1)

3.2.2 场景2 下不同策略的调度结果

为了验证本文所提策略在多种情形下的适用性，本节采用规模较大的系统，并改变线路故障和损坏道路的数量和位置，将其作为场景2 进行重复的实验论证。场景2 相关设定与说明详见附录C。

在该故障场景下，S1、S2 和S3 开关动作后的配电网拓扑均如附录C 图C3 所示，被恢复负荷的加权数量NW分别为11 883、13 626、14 642，而具体的负荷恢复情况如图C4 所示。系统规模的扩大以及故障线路和损坏道路数量的增加使3 种策略的效果差异更加明显，但仍可以得出与上文相似的结论，验证了本文所提策略在不同规模的系统以及多种情形下的适用性与有效性。场景2 的其余仿真结果详见附录C。

3.2.3 探究道路抢修对负荷恢复效果的辅助作用

本节将探究是否计及道路抢修的协调配合所造成的负荷恢复效果的差异，以此验证将道路抢修和电动公交能量的时空调度进行耦合考虑对负荷恢复的重要性。增设S4 为负荷恢复部分和道路抢修部分各自独立决策的对照策略，该策略以2 支抢修队完成各自的抢修任务并返回抢修站所需的时间之和最小为目标函数确定抢修顺序，不顾及配电网方的需求，即道路抢修服务并不辅助负荷恢复服务。S4与本文所提策略的对比如图5 和表3 所示。

图5 S3 和S4 的重要负荷恢复情况对比Fig.5 Comparison of critical load restoration situations in S3 and S4

从表3 中NW的数值和图5 可以看出，2 种场景下的S3 都比S4 具有更好的负荷恢复效果。这是因为S3 中的道路抢修队以协助电动公交尽快到达指定充放电站为目标决策道路的抢修顺序，而S4 中的道路抢修队以自身完成任务并返回的时间最短为目标决策道路的抢修顺序，导致S4 中的电动公交受损坏道路的影响较大，到达充放电站的时间较晚，进而对负荷恢复效果产生不利影响。虽然S4 可以在一定程度上缩短道路抢修队的总花费时间，但在极端灾害发生后，应当以恢复重要负荷的电力供应为首要目标。因此，在负荷恢复过程中计及道路抢修队的行为决策，耦合考虑道路抢修的辅助作用，可以在特殊时期统筹规划各救灾部门之间的协调配合，提升负荷供电恢复能力，具有一定的优越性与重要性。

表3 S3 与S4 的数值对比Table 3 Numerical comparison of S3 and S4

4 结语

本文提出了一种城市道路抢修辅助重要负荷恢复的电动汽车能量时空分层调度策略。基于配电网和交通路网耦合的场景，验证了该策略在不同规模的系统，以及不同线路故障和道路损坏的情形下的适用性。通过不同策略的对比分析，论证了本文策略的有效性和优越性，得出的结论可总结如下：

1）在负荷恢复的过程中，使用多时段协同负荷恢复模型可以充分发挥能量在时间尺度上的灵活性，将有限的能量合理地分配在各个时段，使得权重较高的负荷可以优先获得更长时间的供能，因此S2比S1 具有更好的负荷恢复效果。

2）通过预先的优化决策将电动汽车合理地分配至各个充放电站点可以充分发挥电动汽车所具有的空间灵活移动特性，优化各充放电站的功率和能量配置，实现了电动汽车能量的空间优化调度，因此S3 比S2 的负荷恢复效果更好。

3）在负荷恢复过程中计及道路抢修的辅助作用可以统筹规划各救灾部门之间的行动，优先抢修电动汽车需要经过的路段，节省了电动汽车行驶途中花费的时间与能耗，因此S3 比S4 具有更好的负荷恢复效果。

由于本文以重要负荷的供电恢复为主要研究目标，道路抢修部门的利益并未得到顾及，其行为决策仅以配合供电部门为目标进行优化。而且模型中的不确定性因素也没有得到考虑，分阶段的优化方法还会影响结果的最优性。在未来的研究中，将深入研究极端灾害过后配电网和交通网之间的双向影响，兼顾道路抢修部门和配电恢复部门双方的利益，实现两者间的协同优化决策。同时，深入考虑道路通行速度、道路损坏情况等不确定性因素，进而建立一个考虑城市道路和电力负荷协同恢复的统一随机优化模型。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。