“车-路-网”模式下电动汽车充放电时空灵活性优化调度策略

郑远硕，李 峰，董九玲，罗劲瑭，张 敏，阳小龙

（1. 北京科技大学计算机与通信工程学院，北京市 100083；2. 国网四川省电力公司经济技术研究院，四川省成都市 610041）

0 引言

电动汽车（electrical vehicle，EV）作为负荷侧灵活性资源，不仅有助于新型电力系统建设，还是实现“碳达峰、碳中和”目标的重要工具［1］。EV 兼具交通工具和电力负荷属性，随着EV 保有量规模的扩张，其行驶行为和充电习惯将对路网的交通流量和电网的运行状态带来一定的影响［2］。因此，采取有效的调控策略对EV 的充电行为进行合理的引导，可以缓解EV 行驶和充电过程对路网和电网的冲击作用［3］。

针对EV 与电网交互的调控策略研究［4］，文献［5］制定了智能充电策略，在满足EV 充电需求的同时对系统负载曲线和充电成本进行优化。文献［6］提出了最优双层调度的混合整数规划数学模型，在潮流和EV 出行需求约束下使配电网整体的负荷方差最小。文献［7］提出了EV 移动储能与可再生能源协同电动汽车与电网互动（V2G）策略，实现对可再生能源的合理消纳，平抑等效负荷波动性。文献［8］提出了基于V2G 辅助服务的配电网日前调度方法，该方法可有效降低负荷峰谷差和系统网损，缓解线路的电压越限状况。文献［9］从电网运营商、EV用户和聚合商的角度对最新的EV 分布式充电控制方案进行了探讨，为分布式优化算法的研究提供参考。

针对EV 与路网交互的调控策略研究［10］，文献［11］提出了一种基于实时群智感知技术的EV 最优路径选择策略，以减少EV 行驶时间和总充电成本［11］。文献［12］利用Dijkstra 算法为EV 规划耗时最短的行驶路径，并运用模糊控制方法对V2G 响应功率和容量进行了评估。文献［13］构建了实时动态路况能耗预测模型，结合交通路况的时变性规划EV 的充电路径。文献［14］提出了下一目的地导向下的EV 充电导航策略，在降低EV 行驶时间成本和距离成本的同时实现了充电站间的设备利用率均衡分布。文献［15］提出了综合考虑交通网、充电站、配电网信息的EV 充电路径规划方法，该方法可有效规划前往充电站的车辆数目，在提高充电设施利用率的同时缩短EV 充电等待时间。

但上述两类充电调度策略仅限于EV 与电网或路网间的交互场景，并未协同考虑EV、充电站、路网以及电网间的交互影响［16］。因此，文献［17］提出了基于路-电耦合网络的电动出租车快速充电引导及其定价策略，在合理调控充电负荷的同时降低了充电站的内部拥堵率。但其在为EV 规划路径时假设EV 位于某个节点上，而实际上，EV 大概率处于路网节点之间，未能根据实时位置给EV 提供导航。文献［18］在深入研究“车-站-路-网”系统模型的基础上提出了时空分布电价优化策略，通过对EV 充电行为的调控来减小电力网损耗和电压偏移，但未分析该策略对EV 用户充电成本的影响。文献［19］从充电网络运营商的角度构建城市交通网和配电网耦合的双层优化模型，分析了电价调控策略对配电网、交通网和EV 用户收益的影响，但模型中并未考虑行驶时间成本对EV 用户充电决策的影响。

因此，本文提出基于“车-路-网”交互的EV 充放电时空灵活性优化调控策略。首先，构建动态路网模型并结合改进的Floyd 算法精确模拟EV 的行驶路径。其次，结合EV 出行时刻及初始电量信息预测EV 充电负荷时空分布情况。然后，提出计及EV出行时间成本的主从博弈模型对EV 充电负荷的时空分布情况、充电站周围路网的交通流量和EV 用户的收益进行多目标优化调控。最后，以中国北京市某区域路网为例，分析EV 充电行为对路网、配电网、充电站和EV 用户的影响，验证本文模型的有效性。

1 “车-路-网”交互模型

1.1 路网模型

1.1.1 动态路网模型

在“车-路-网”交互模式中，路网一般采用静态模型，交通流量为非时变的。为了反映路网动态变化的特点，本文构建动态路网模型，以1 h 为单位更新各路段流量，动态路网模型可表示为：

式中：G为路网集合；V为路网中所有节点的集合，共有u个；E为路网中路段的集合；H为划分的时间段集合，即将全天划分为T个时间段；W为路段权值的集合；vi为第i个路网节点；vij为连接第i个和第j个路网节点的路段；wij(t)为t时段路段vij的权值。路网集合G中各节点间的连接关系用邻接矩阵D来描述。矩阵D的元素dij(t)的表达式为：

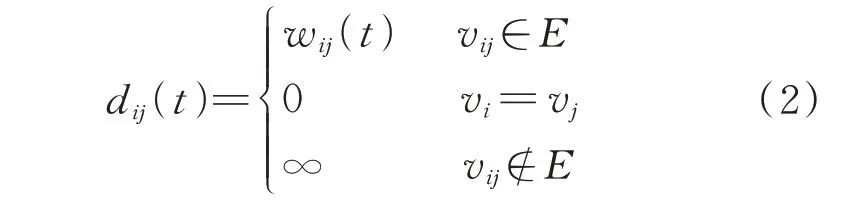
1.1.2 城市道路路阻模型

行程时间为EV 用户出行最关心的路阻因素，因此，本文选择行程时间作为道路路阻进行建模分析。行程时间由道路长度与行驶速度决定，而行驶速度又受到道路容量和车流量影响，故本文引入速度-流量模型计算车辆实时行驶速度，进而得出EV用户的行程时间。EV 行驶速度υij(t)的数学表达式为［20］：

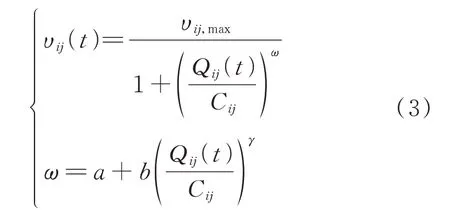
式中：υij，max为路段ij自由流速度；Cij为路段ij的道路通行能力；Qij(t)为t时段路段ij的车流量；a、b、γ为道路等级自适应系数。路阻模型表达式为：

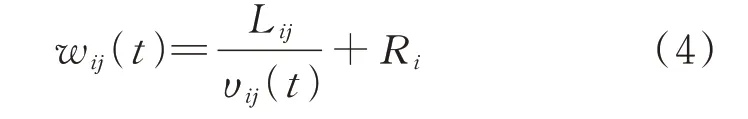
式中：Lij为路段ij的长度；Ri为路口i的信号灯等待时长。

1.2 配电网模型

本文基于IEEE 33 节点标准配电网模型。本文的重点在于探究海量EV 的充电行为对电网的负荷时空分布、路网的交通路况以及充电站和EV 用户的收益带来的影响。因此，配电网将作为电能供应商与充电站通过电能的双向交易进行互动。第g个配电网节点的模型表达式为：

式中：GP和CP分别为源节点的位置和容量信息。

1.3 EV 电价响应度模型

一般情况下，EV 用户会选择距离其最近的充电站进行充电，但这样可能会引起某个充电站在某个时间段的负荷越限，严重影响配电网的稳定运行。此外，在充电高峰期位于路网节点密集区域的充电站周围路段的交通流量会增大，可能引发交通拥堵。因此，需要制定合理的调控策略引导EV 用户的充电行为，以均衡各个充电站的负荷分布情况，改善充电站周围路段的交通流量情况。调控机制如附录A 图A1 所示。

1.3.1 充电电价响应度模型

EV 用户参与调控存在价格启动阈值和饱和阈值。充电站间的电价差高于启动阈值时EV 用户接受调控，改变对充电站的原有选择；若电价差高于饱和阈值时再持续增大，响应充电调控的EV 用户不再增加。 EV 用户需求响应度λc的数学表达式为［21］：

式中：Δck，m(t)为t时段第k个充电站与第m个充电站的电价差值；λc(t)为t时段的需求响应度；λc，max为最大需求响应度；lk，m和hk，m分别为EV 用户对第k个充电站与第m个充电站之间电价差额的需求响应的启动阈值和饱和阈值。当电价差低于lk，m时，EV用户不愿参与需求响应；当电价差超过hk，m时，EV用户响应度达到最大；当电价在[lk，m，hk，m]区间时，EV 用户响应度呈线性增长。

1.3.2 放电电价响应度模型

EV 作为灵活的调度资源，可通过V2G 技术与电网进行电能的双向交易，在缓解电网用电压力的同时提高EV 用户的收益。因此，本文根据电量需求制定放电价格策略，引导EV 用户在用电高峰期放电。EV 用户放电响应度与放电价格的关系为：

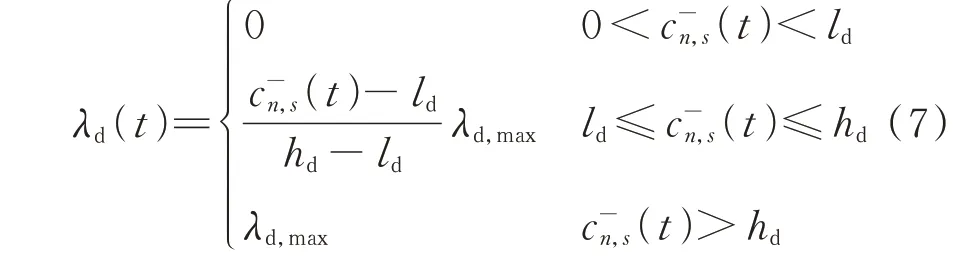
式中：λd(t) 为EV 用户对放电电价的响应度；(t) 为t时段第n辆车在第s个充电站的放电电价；ld和hd分别为放电响应的启动阈值和饱和阈值；λd，max为最大放电响应度。

1.4 “车-路-网”交互机理

“车-路-网”之间的交互主要通过充电站作为接口，交互模式如附录A 图A2 所示。EV 的充电行为与电网对充电站的供电行为作为交互过程。充电站作为电网与路网的交互媒介（假设其与路网节点i和电网节点g连接），则在t时段充电站s的总充电负荷Ps(t)可表示为：

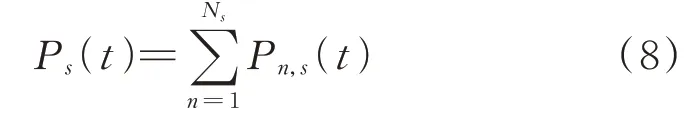
式中：Pn，s(t)为t时段第n辆EV 在第s个充电站的充电负荷；Ns为第s个充电站进行充电的EV 总数。

2 EV 充电负荷时空预测模型

2.1 EV 充电负荷影响因素

2.1.1 充电行为特性

EV 用户根据充电触发阈值判断此时EV 是否需要充电。当电量低于充电触发阈值时，EV 用户选择就近充电，当电量达到EV 用户的期望值后继续行驶。

2.1.2 出行时段信息

EV 的起始充电时段是影响充电负荷的关键因素。EV 的出行会出现早、晚高峰等多峰分布的情况，普通的正态分布无法对EV 的出行时段分布情况进行实际的刻画。因此，本文采用高斯混合模型对EV 的出行时段分布进行拟合。EV 出行的概率分布函数p(x|Θ)的表达式为［22］：

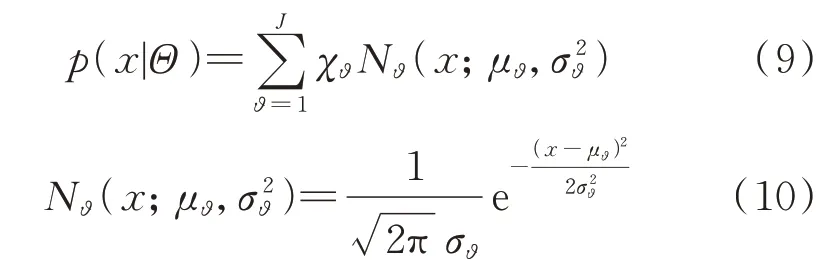
式中：Nϑ(·)为第ϑ个高斯分量函数；J为高斯分量的个数；χϑ为第ϑ个高斯分量的权重；Θ={θ1，θ2，…，θϑ，…，θJ}为元素集合；μϑ为平均值；σ2ϑ为方差。

2.1.3 EV 初始荷电状态（SOC）信息

假设EV 的SOC 随行驶距离线性下降，则EV接入电网时的SOC 为：

式中：E0为EV 的初始SOC，且E0∈(0，1)；d为EV每天的行驶距离，其服从对数正态分布［23］；τ为EV充电后的行驶天数；dR为EV 最大行驶路程。

EV 初始SOC 的概率密度函数Pd(E0；ψ，σ)的表达式为：

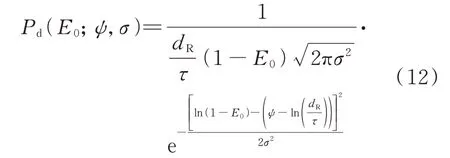
式中：ψ为日行驶里程均值；σ为概率函数的标准偏差。

2.2 基于改进Floyd 算法的EV 充电负荷预测模型

EV 充电需求预测是研究“车-路-网”互动的重要前提［24］。本节对理想状态下EV 用户的充电负荷进行预测，为第3 章的EV 充放电优化调控策略提供先验知识。在此背景下，不考虑路阻对EV 的影响，且EV 均选择距离自己最近的充电站进行充电。预测步骤见附录B，预测流程如附录B 图B1 所示。

3 EV 充放电需求时空灵活性优化调控模型

3.1 基于主从博弈的充电站-EV 多目标优化模型

使用价格响应的方式来引导EV 充放电可以避免变量维数灾难问题，EV 根据不同充电站发布的电价选择对自己收益最大的充电站进行充电。充电站与EV 之间自然地构成了主从博弈，其中充电站为领导者，EV 为追随者。充电站作为领导者，其决策变量为t时段第n辆EV 在第s个充电站的充电电价(t)和放电电价(t)；EV 作为追随者，其决策变量为t时段第n辆EV 在第s个充电站的充电功率(t)和t时段第n辆EV 在第s个充电站的放电时长ΔTdis，n，s(t)。

3.1.1 充电站目标函数

充电站的目标为最大化自身的收益，其收益由2 个部分组成：一是充电站与EV 间的充放电收益；二是充电站和电网间的购电、售电收益。综上，充电站目标函数的表达式为：

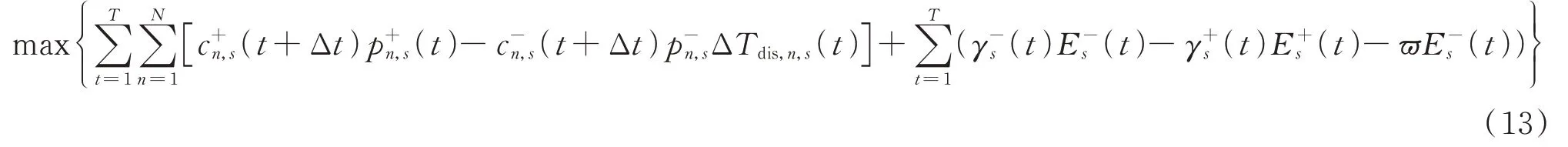
式中：N为在充电站进行充电的EV 总数；Δt为EV在行驶过程中因路阻造成的延误时长；p为第n辆EV 在第s个充电站的放电功率(t)、(t)、(t)和(t)分别为t时段第s个充电站与电网的购电电价、售电电价、购电电量和售电电量；ϖ为充电站与电网进行放电时电池退化费用率。

3.1.2 EVCS 约束条件

1）充电电价约束

2）放电电价约束

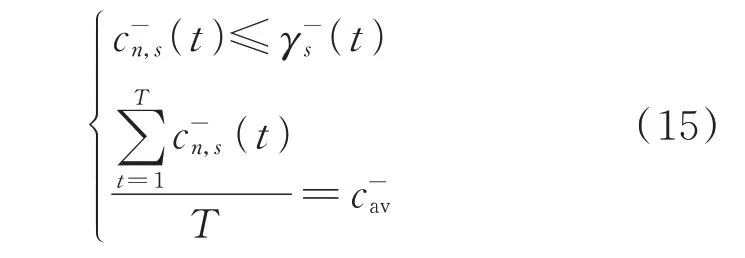
3）充电站负荷约束

式中：Ps(t)为第s个充电站在t时段的负荷；Ps，max(t)为第s个充电站在t时段的最大负荷。

4）充电站日前购电量、实时购售电量约束

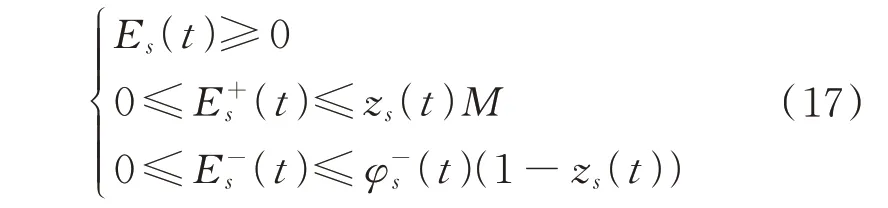
式中：Es(t)为第s个充电站在t时段的日前购电量；zs(t)为第s个充电站在t时段的布尔变量；M为一个充分大的正数；(t)为第s个充电站在t时段储能的放电量。

5）能量平衡约束

6）储能充放电量约束

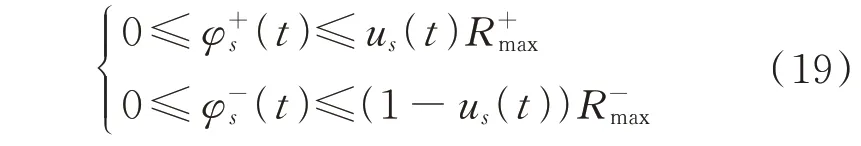
式中：us(t)为t时段第s个充电站的布尔变量；R和R分别为储能最大充电功率和最大放电功率。

7）储能电量约束

式中：S(t)为t时段充电站的储能电量；η+和η-分别为储能充电效率和放电效率；Smax为储能设备最大容量。

8）EV 参与调度条件

不同充电站电价差大于需求响应启动阈值时EV 参与调度，则有

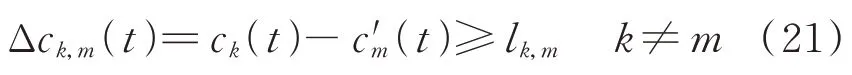
式中：ck(t)为EV 参与调度前第k个充电站t时段的分时电价；c′m(t)为EV 用户参与调度后第m个充电站t时段的分时电价。

3.1.3 EV 目标函数

EV 的目标函数由4 个部分组成：1）EV 向充电站放电的收益以及EV 的充电成本；2）EV 放电引起的电池退化成本；3）EV 充、放电过程中电能传输损耗成本；4）由于路阻引起的时间延误造成EV 用户的经济损失。综上，EV 目标函数为：

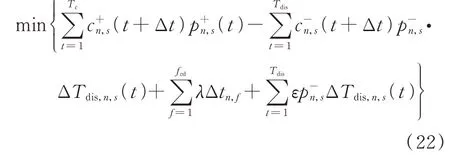
式中：Tc为EV 充电时段；Tdis为EV 放电时段；ε为EV 电池退化费用率；Δtn，f为第n辆EV 在第f次充放电行程中由于路阻引起的延误时长；fcd为EV 充放电次数；λ为时间成本系数。

3.1.4 EV 约束条件

1）EV 电池荷电水平约束

EV 的充电量应使电池达到相应的荷电水平，约束条件为：

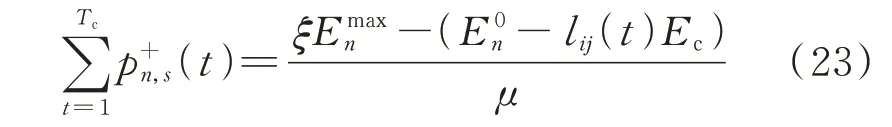
式中：ξ为EV 用户期望的荷电水平，考虑到对电池的保护作用，令ξ=0.9；Emaxn为第n辆EV 的电池容量；E0n为第n辆EV 电池的初始电量；lij(t)为t时段EV 发出充电请求的路网节点i到其选择的充电站的路网节点j之间的距离；Ec为EV 每千米的耗电量；μ为EV 的充放电效率。

2）充电功率约束

接入电网的EV 充电功率不应超过其最大充电功率的限制，约束条件为：

3）放电时长约束

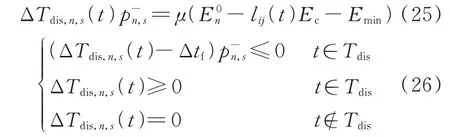
式中：Δtf为峰值时间；Emin为EV 荷电量最小值。

本节采用KKT 条件将充电站-EV 多目标优化模型转化为混合整数线性规划模型并进行求解，具体的求解过程见附录C 第C1 章。

3.2 EV 充放电优化调控策略

结合EV 电价响应度模型、EV 充电负荷时空分布预测模型和充电站-EV 多目标优化模型，提出基于“车-路-网”交互的EV 充放电优化调控策略，调控流程如图1 所示，调控步骤见附录C 第C2 章。

图1 EV 充放电优化调控流程图Fig.1 Flow chart for optimal dispatch and control of EV charging and discharging

4 算例分析

4.1 算例设置

本文采用北京市某区域路网结合IEEE 33 节点配电系统对上述模型进行算例分析。其中，区域周长为42.5 km，面积约为100 km2，道路数量为106 条，道路平均长度为1.44 km，路网节点数为70 个。该区域共配置3 个10 kV 配电网。单个10 kV 配电网不能从规模上与路网匹配，因此，使用3 个配电网覆盖充电站及其周围区域［25］。参考充电设施规划，共建立15 个充电站，分布于3 个10 kV 配电网内，充电站节点编号为51 至55 和61 至70。结合2020 年人口普查结果，针对该区域的人口数量以及拥有的车辆数，引入10 000 辆EV，考虑到EV 用户可能会存在“里程焦虑”的情况，结合SOC 的分布情况，设置参与充电的车辆数为1 890 辆［26］。算例分析环境为MATLAB 2021a，使用CPLEX 求解器进行求解。路网参数及其他实验参数见附录D 表D1 和表D2。

4.2 算例结果及分析

4.2.1 不同交通状态对EV 行驶路径的影响

路网的交通流量状况会影响EV 用户的路径选择，如图2 所示。绿色线条为不考虑路阻影响时EV的行驶路径，此时，EV 用户将选择距离最短的路径行驶。红色线条为模拟实际路网交通状态下利用改进的Floyd 算法为EV 用户规划的行驶路径。在路阻的影响下，距离最短路径与时间最短路径不一定相同。因此，为了节约时间成本，EV 用户将会选择时间最短路径进行行驶。当EV 行驶到某一位置时（EV 位于两节点间），其电量下降到充电触发阈值，EV 发出充电请求，如图2 中橙色节点所示。本文算法可以对EV 进行精确寻址而不局限于假设其位于路网节点上，减小估计EV 所需充电量的误差，提高对EV 用户收益估算的准确度以及对充电站充电负荷预测的精度。然后利用改进的Floyd 算法为EV用户规划到充电站的时间最短路径，满足EV 的充电需求。综上，利用改进的Floyd 算法可以在实际的路网交通状况下最小化EV 用户的行驶时间，且可以实现对EV 的精确寻址，验证了本文改进的Floyd 算法的有效性。

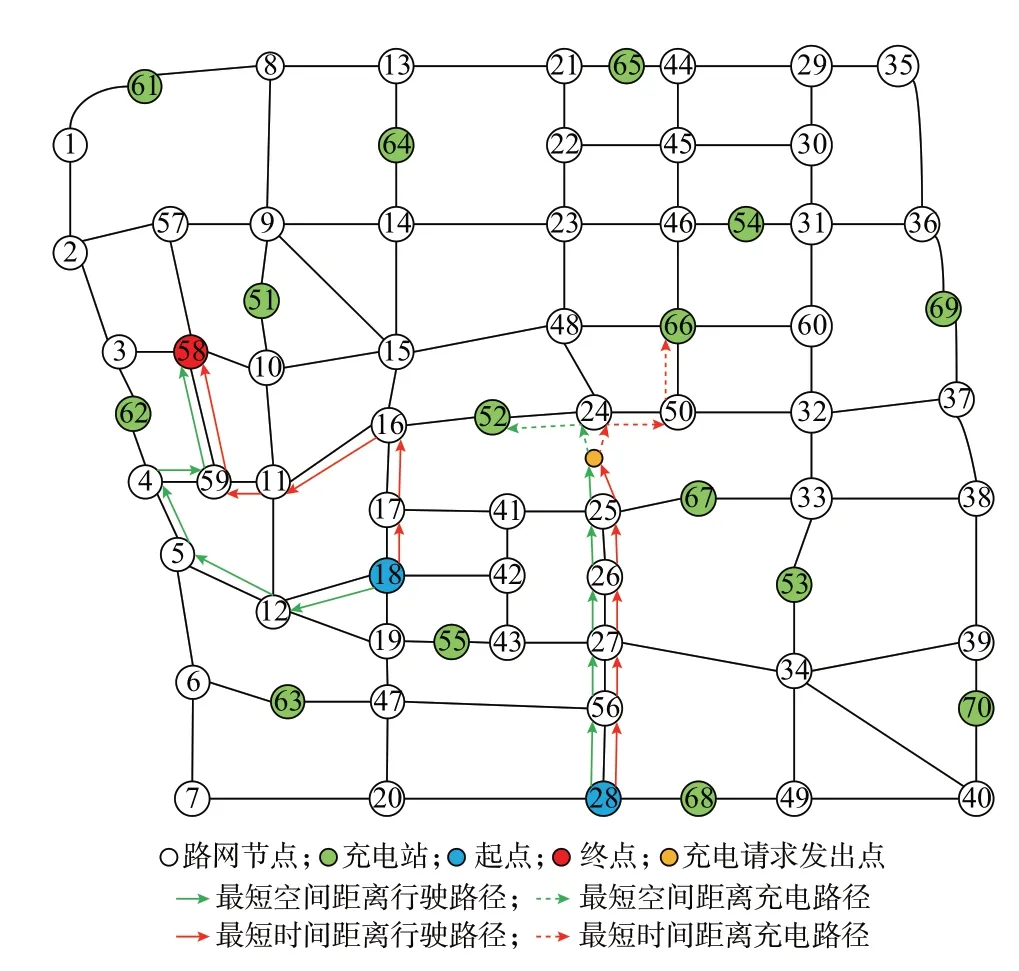
图2 不同交通状况下EV 用户的行驶路径选择Fig.2 Driving path selection for EV users under different traffic conditions

4.2.2 充电负荷预测结果

大多数EV 用户通常会根据自己的出行需求并结合车辆的SOC 选择是否需要充电。由于EV 的移动特性使得充电负荷具有时空交互性。充电负荷预测是负荷调控的基础，因此，需要利用2.2 节的预测模型对EV 用户的充电负荷时空分布情况进行预测。为了验证预测结果的准确性，将预测结果分别与EV 用户的出行规律模拟曲线及EV 充电数据拟合曲线进行对比，如附录D 图D1 和图D2 所示。在图D1 中，EV 充电负荷预测结果的包络线与EV 用户的出行规律曲线基本吻合，可从定性角度验证预测结果的准确性。为了进一步验证预测结果的准确性，本文结合EV 充电数据对预测结果进行定量分析。对图D1 中充电负荷预测结果进行拟合，得到图D2 中预测结果的拟合曲线。由图D2 可以看出，充电负荷预测结果拟合曲线与EV 充电数据拟合曲线的走势相似度较高，充电高峰期均出现在08：00—09：00 时段，预测结果拟合曲线的峰值为9.56 MW，EV 充电数据拟合曲线的峰值为9.13 MW。

在对EV 总负荷预测的基础上，本文进一步利用预测模型分析EV 充电负荷的时空分布特征，为后续的充放电调控工作提供参考。图3 给出15 个充电站充电负荷的时空分布情况。

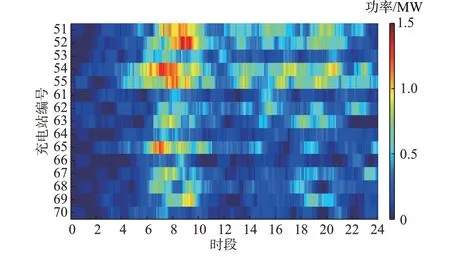
图3 EV 充电负荷时空分布特征Fig.3 Spatio-temporal distribution characteristics of EV charging load

结果表明：1）充电站节点53、61、64 和66 的负荷相对较低，充电站节点51、52、54、55 和65 的负荷较高。由图2 路网的拓扑结构可知，充电站节点51、52、54、55 和65 位于路网中心或路网节点较为密集区域，车流量较大，充电负荷较高；2）充电站节点51、52、54、55 和65 的充电高峰期出现在07：00—10：00 时段，与附录D 图D1 中EV 用户的出行规律曲线和图D2 中EV 充电数据集曲线的高峰期的出现时段较为吻合。

4.2.3 调控结果对配电网的影响

根据4.2.2 节对充电站的负荷时空分布情况预测结果，利用本文所提的优化调控策略对EV 的充电行为进行合理引导。在调控过程中，不仅要考虑到充电站负荷的时间分布特性，还要结合EV 用户的充电便利性考虑充电站的空间分布特性。由图3 可知，充电站节点51 的深颜色区域出现在07：00—10：00 和18：00—21：00 时段，由图2 的路网拓扑结构可知，距离充电站节点51 路程较短且同一时段充电负荷较低的为充电站节点61。同理，利用本文所提的优化调控策略对其余充电站EV 充电的行为进行合理的引导，调控信息如表1 所示，调控后EV 充电负荷时空分布状态如图4 所示，调控前后充电站负荷变化情况如附录D 图D3 所示。

表1 EV 充电行为调控信息Table 1 Dispatch and control information for EV charging behavior

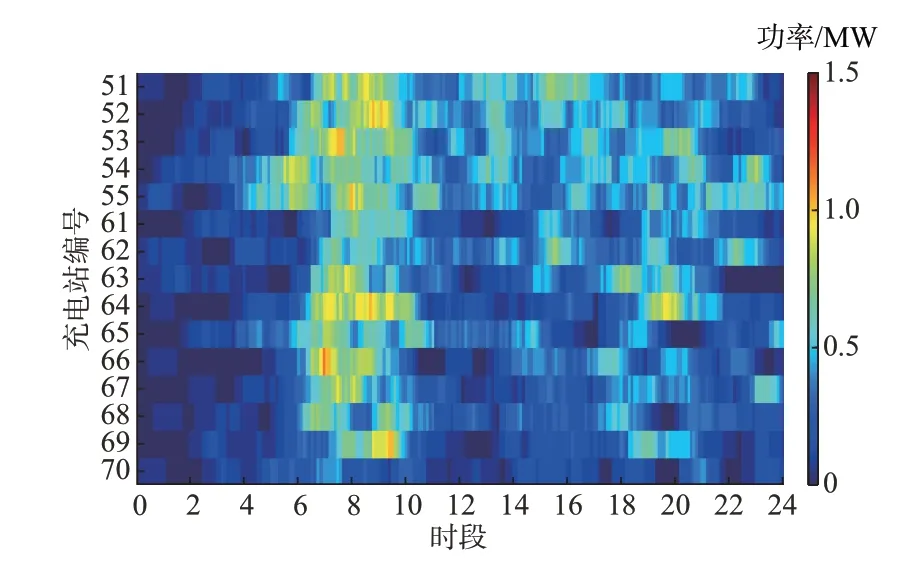
图4 调控后EV 充电负荷时空分布Fig.4 Spatio-temporal distribution of EV charging load after dispatch and control

由表1 可以清楚地了解到充电站间EV 数量和充电负荷的转移情况，图4 直观地呈现参与调控的充电站优化后负荷的发布情况。与调控前EV 充电负荷时空分布情况（图3）相比，充电站节点51、52、54、55、65 的负荷在调控时段有所降低，对应的区域颜色由深变浅，充电站节点53、61、64、66 的负荷在调控时段有所提高，通过负荷的转移实现充电站间负荷均衡分布。附录D 图D3 直观地反映充电站调控前后负荷的升高或降低情况。充电站节点51 在07：00—10：00 时段和18：00—21：00 时段负荷降低，对应的充电站节点61 在这2 个时段负荷提高，与表1 的调控充电站和调控时段吻合，分析其他参与调控的充电站可得到一致的结论。

最后，为评估EV 充电负荷对配电系统运行的影响，本文以配电网功率潮流分布特性为例，在无序和有序（利用本文所提的调控策略）场景下进行分析，结果如图5 所示。结果表明：1）配电网功率潮流分布曲线在负荷早高峰（07：00—09：00）时段涨幅较大，与附录D 图D1 中的EV 出行规律分布相似，说明本文潮流分布规律符合EV 充放电负荷对配电网系统的影响；2）经过有序调控后配电网潮流分布在高峰处被分流，低谷处被填充，相比于无序情况，有序调控后配电网功率潮流分布曲线相对平缓，对配电网的安全稳定运行起到一定的保障作用。

图5 不同场景下配电网功率潮流的分布特性Fig.5 Distribution characteristics of power flow for distribution network in different scenarios

4.2.4 调控结果对路网的影响

为分析调控结果对路网的影响，本节以充电站节点52 和64 为例对2 个充电站所处路段的车流量情况进行分析，如图6 所示。充电站节点52 所在路段调控后相比于调控前车流量显著降低，该路段拥挤程度有所改善，在车流量最大的时刻（08：00），EV数量由98 下降到87，降低了11%，这是因为调控策略引导部分车辆前往充电站节点64 进行充电。充电站节点64 所在路段车流量相比调控前明显增大，在08：00 时，EV 数量由19 上升到33，增加了42%。综上，调控策略起到了分流的作用，在一定程度上缓解了充电站所处路段的拥挤状态。

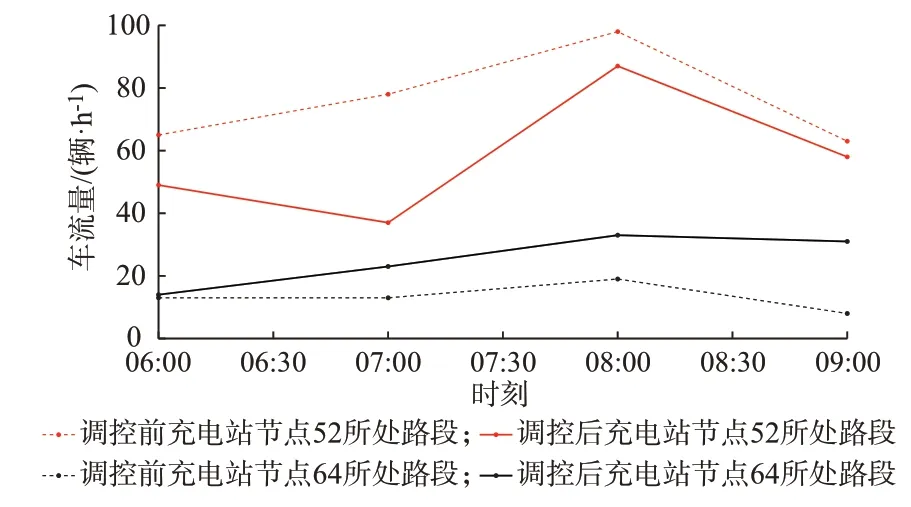
图6 调控前后充电站所在路段EV 数量的变化Fig.6 Changes in number of EVs on road sections where charging stations are located before and after dispatch and control

4.2.5 调控结果对充电站的影响

为了了解不同电价调控策略对充电站收益的影响，本节对2 种电价方案下15 个充电站的总收益进行分析，如表2 所示。方案1 为基于主从博弈模型的充电响应度模型优化电价（本文调控策略采用的电价方案）；方案2 为利用充电响应度模型对日前电价（充电站向电网购电的价格）进行调整得到的电价。结合日前电价可计算出充电站向电网购电的成本为96 282 元，采用不同方案充电站的营收情况如表2 所示。方案1 电价和方案2 的日前电价［27］分别如附录D 表D3 至表D13 所示。采用方案1 充电站盈利1 420 元，采用方案2 充电站亏损822 元，由此验证本文所提模型的有效性和可行性。

表2 不同电价方案下充电站营收情况统计Table 2 Statistics on electricity trading of charging stations with different electricity price schemes

4.2.6 调控结果对EV 用户的影响

结合本文所提的调控策略对EV 用户的充电行为进行引导，调控前EV 用户的充电成本为98 907 元，调控后EV 用户的充电成本为97 702 元，调控后EV 用户的充电成本降低了1 205 元。

为了缓解电网高峰期的用电压力，本节结合1.3.2 节中的放电电价响应度模型合理引导EV 用户参与V2G 交易。在此过程中，EV 用户也可获得相应的收益。结合附录D 图D1 中EV 充电负荷预测结果以及图3 充电站负荷的分布情况可知，充电高峰期出现在07：00—10：00，对应的充电站节点为52、54 和55，因此，将这3 个充电站作为放电目标充电站。放电情况如表3 所示，放电电价及相关参数见附录D 表D14 和表D15。

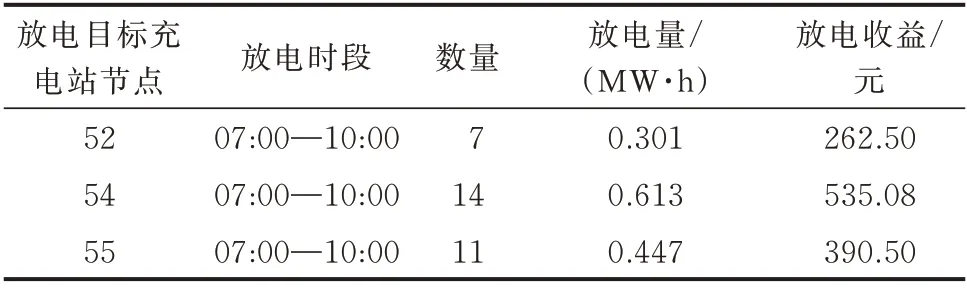
表3 EV 放电情况统计Table 3 Statistics of EV discharging

此外，在构建主从博弈模型时，考虑到EV 用户出行成本对EV 充电成本的影响，调控前后EV 用户的出行时间分别为351.35 h 和331.03 h，出行时间减少了20.32 h。文献［28］中出行时间成本系数的取值为50.944 元/h，因此，总出行时间成本减少了1 035.18 元。

5 结语

为充分发挥EV 作为灵活性资源的潜力，本文提出“车-路-网”模式下电动汽车充放电时空灵活性优化调控策略以合理引导EV 的充放电行为。该策略可对EV 负荷的时空分布情况、充电站附近路网的交通流量情况以及EV 用户的收益进行多目标优化。最后结合IEEE 33 节点配电系统，以北京市某区域为例对该模型进行验证，实验结果表明：

1）本文提出改进的Floyd 算法可精确模拟EV的行驶路径，为预测EV 充电负荷分布特性提供实验基础。

2）本文提出的调控策略可实现充电站间电量转移共计10.114 8 MW·h，通过负荷的转移实现充电站间负荷分布均衡。

3）本文提出的调控策略在车流量最大的时刻通过分流缓解了充电站所处路段的拥挤情况。

4）本文所提调控策略使充电站盈利1 420 元。

5）本文所提调控策略可降低EV 用户的充电成本为1 205 元，此外，EV 用户的放电收益为1 188.08 元。

“车-路-网”的交互主要通过充电站作为接口。因此，后续的研究工作将重点关注充电站布局的优化问题，找到既能满足路网通行效率和配电网运行效率最高，又能使出行者自身出行效用最大化的充电站布局。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。