扭王字块体护面斜坡堤胸墙受力的数模试验研究

孙大鹏，刘 飞，修富义，王 键，赵沛泓，董 胜

(1.大连理工大学 海岸和近海工程国家重点实验室，大连 116024；2.长春中海地产有限公司，长春 130000；3.沈阳龙湖新北置业有限公司，沈阳 110000；4.中交第一航务工程勘察设计院有限公司，天津 300222；5.中国海洋大学，青岛 266100)

在波浪的作用下，斜坡堤的胸墙易发生损坏，而水平波浪力是胸墙损坏的主要原因。对于斜坡堤胸墙水平波浪力的确定方法，大致分为物模试验和数值模拟两种。而相较于物模试验方法，数值模拟有着成本低、易操作性强、不受比尺因素影响等优点，故众多学者对波浪与斜坡堤相互作用展开了数值模拟研究。李雪艳[1]应用BFC-VOF方法模拟胸墙结构所受波浪力的不同特性。LU Y J[2]采用细化局部网格方式精确求解斜坡堤胸墙受力值，为FLUENT数值模拟胸墙受力做出了重要贡献。Kobayashi[3]和Hu[4]曾在斜坡堤数值模拟方面有过突出贡献，借助数值模型进行无块体护面条件下波浪与斜坡堤相互作用的全过程模拟计算。Losada[5]和Guanche[6]为了验证COBRA-UC模型的有效性，先期开展物模试验，并在此基础上进行斜坡堤胸墙水平波浪力的数模研究，并经过有效的数据比对，最终确定使用COBRA-UC模型的方法有效；张九山[7]为解决护面块体数值模型问题，引入多孔介质区，创新性的将动量源项加入N-S方程，并基于数模与物模的一致性，最终表明在数值模型中引入多孔介质区可以有效模拟护面块体；王鹏[8]应用FLUENT数值模拟，通过添加多孔介质区，数值模拟块体护面斜坡堤与波浪的作用过程，建立了糙渗系数与惯性阻力系数的关系。孙大鹏[9]借助FLUENT软件平台，展开扭王字块体护面斜坡堤越浪量的数模试验研究，结合物模试验结果，给出斜坡堤越浪量的数模计算经验公式。上述学者的数模实践通常把斜坡堤上的护面块体概化成多孔介质，并借助物模试验确定多孔介质区的特征参数(如惯性阻力系数或糙渗系数等)，进而实现胸墙水平波浪力的数值模拟。由于确定多孔介质区的特征参数是建立数值模式的前提条件，而如上的研究历程表明数值试验成为一种依附于物模试验而非独立的研究手段，且研究成果具有局限性而难于推广应用。

本文针对坡度系数m=1.5的扭王字块体护面斜坡堤，综合考虑相对块体尺寸、相对水深、相对胸墙高度、波陡、相对坡肩宽度和相对堤顶超高影响因素，先期完成胸墙波浪水平力的物模试验[10-11]，并以胸墙波浪水平力的物模试验值为基准，应用FLUENT软件，寻求相应工况下数值模式中惯性阻力系数的对应值，通过多元回归分析，给出以上六种影响因素下的扭王字护面块体惯性阻力系数计算公式。应用该公式，使得斜坡堤胸墙受力可以独立在FLUENT软件进行数值模拟，为斜坡堤胸墙受力的数值研究探寻了一条新途径。

1 数值波浪水槽

1.1 水槽概况

本文基于唐蔚[12]和王键[13]波浪数值水槽的造波方式，采用主动吸收式造波来消除二次反射，建立了数值波浪水槽(图1)，其中造波边界设置在水槽左侧，将6 m长的消波区设置在水槽末端，水槽全长25 m、高0.8 m。为进行精确的斜坡堤胸墙受力数值模拟，斜坡堤堤角位置设置在距造波端边界5～6倍波长以外，以保证入射波浪的稳定性。

图1 数值波浪水槽(单位：m)Fig.1 Numerical wave tank

1.2 数值波浪水槽性能验证示例

采用JONSWAP谱不规则波(γ=3.3)，在水槽中距造波边界15.0 m和19.0 m两处设置波面采集仪，用采集到的波面信息验证数值水槽的有效性，靶谱与模拟谱对比见图2，对比模拟波浪与目标波浪的统计波浪要素见表1。其中：d为水深,m；Hs为有效波高，m；Tp为谱峰周期，s。

表1 波浪要素值比对Tab.1 Wave element value comparison

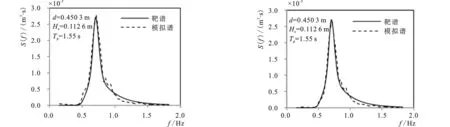
2-a 距造波边界15.0 m 处2-b 距造波边界x=19.0 m处图2 数值水槽性能验证Fig.2 Performance verification of numerical tank

由表1和图2可以看出，在频谱与波要素方面，目标波浪与模拟波浪具有很好的一致性，验证构建的数值水槽能够满足本文数值模拟要求。

2 多孔介质区中惯性阻力系数C的率定

2.1 数模工况组合

采用FLUENT进行数值模拟计算，应用本文构建的数值波浪水槽，在水槽试验段摆放带有胸墙的扭王字块体护面斜坡堤模型(坡度系数m=1.5)，引入多孔介质区模拟扭王字护面块体，参照王鹏[8]的边界条件与数值计算方程，选用三种重量的扭王字块体(均满足稳定性要求)，并将不同重量的扭王字块体以块体尺寸h进行区别，块体尺寸h如图3所示，h依次是4.2 cm、6.0 cm、7.8 cm。

图3 扭王字块体尺寸图Fig.3 Shape of accropode blocks

在满足波浪不破碎的条件下，数值模拟工况组合如表2。

表2 试验工况组合Tab.2 Combination of experimental conditions

2.2 惯性阻力系数C与胸墙水平波浪力的关系

采用表2中15种工况组合，分别模拟计算三种重量的扭王字块体护面情况下斜坡堤胸墙受力过程。本文的研究内容主要围绕数值模拟计算中惯性阻力系数C的确定，如何构建惯性阻力系数C的计算体系，本文采用了下述方法：

以表2中工况1条件下块体尺寸为4.2 cm的C值计算过程为例。应用单一变量控制方法，对惯性阻力系数C值进行率定计算。将C值取为0.1、0.5、1.0、2.0、5.0进行数值模拟计算，获得不同C值计算的胸墙水平波浪力计算值，给出胸墙水平波浪力计算值与C值的拟合曲线(指数型函数)，如图4-a所示。进而以胸墙水平波浪力物模试验值[10]为指针，在图4-a中读出第1种试验顺序条件下h=4.2 cm的扭王字块体的C值。其他数值模拟试验采用相同方式，当h=4.2 cm时，C值的率定结果如图4-a～4-o所示。采用同样方法，分别确定出h=6.0 cm和h=7.8 cm时C值的率定结果。

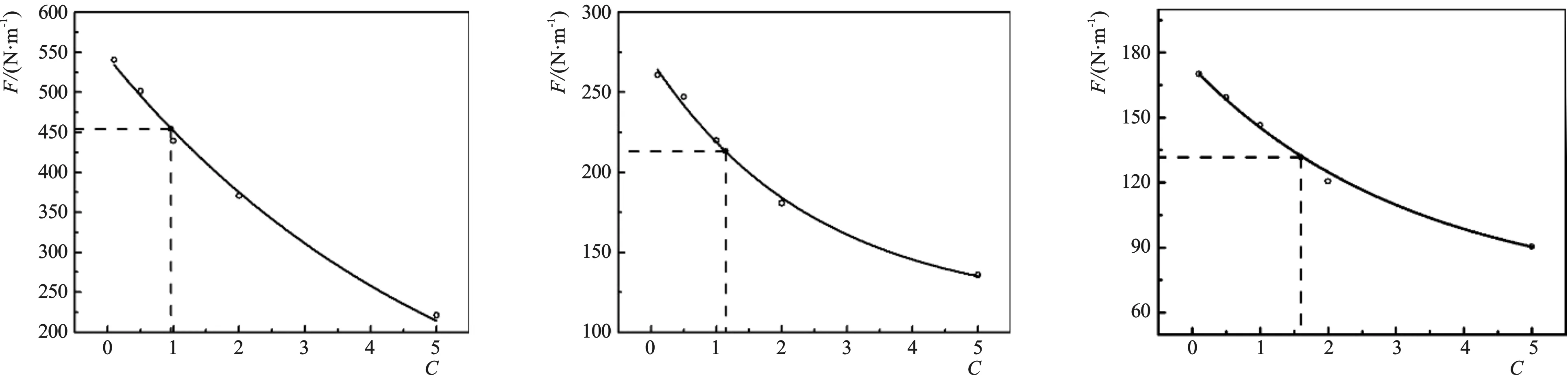
4-a 试验顺序14-b 试验顺序24-c 试验顺序3

采用上述方法确定的惯性阻力系数C值，数值模拟得到的胸墙水平波浪力的计算值和物模试验值的对比如表3所示。

表3 数值计算结果(h=4.2 cm、6.0 cm、7.8 cm)Tab.3 Numerical results(h=4.2 cm，6.0 cm，7.8 cm)

为了验证该数值模拟方法的有效性以及确定C值的准确性，将表3中给出的C值分别代入相应的数值模型中计算各工况下的胸墙水平力值，数模计算值与物模试验值[10]对比如图5所示。

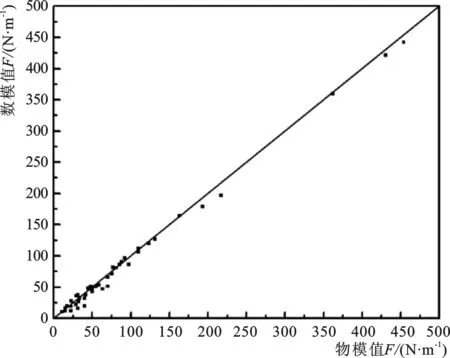
图5 胸墙水平力数模计算值与物模试验值的对比Fig.5 Comparison between numerical results and physical model results of horizontal force on breast wall

如图5所示，数模计算值与物模试验值具有较高的一致性，表明合理引入多孔介质区可以有效模拟扭王字块体在斜坡堤面的作用，同时表明扭王字块体护面斜坡堤胸墙水平波浪力的数值模拟计算值可以通过多孔介质区的惯性阻力系数C值确定。

3 扭王字护面块体惯性阻力系数C的计算公式

(1)

3.1 Hs/L与C值的相关关系

该无因次表达式共计6个影响因素，调整Hs/L的值，控制其他影响因素不变时，C值试验结果如图6所示。从图中可以看出，C值随Hs/L增加而增加，呈线性相关关系，采用线性函数进行拟合。

图6 C与Hs/L的关系Fig.6 Relational graph of C versus Hs/L图7 C与d/Hs的关系Fig.7 Relational graph of C versus d/Hs

3.2 d/Hs与C值的相关关系

该无因次表达式共计6个影响因素，调整d/Hs的值，控制其他影响因素不变时，C值试验结果如图7所示。从图中可以看出，随着d/Hs的变化，C值走向呈二次曲线趋势，采用二次函数进行拟合。

3.4 b1/Hs与C值的相关关系

该无因次表达式共计6个影响因素，调整b1/Hs的值，控制其他影响因素不变时，C值试验结果如图9所示。从图中可以看出，C值随b1/Hs增加而增加，采用指数函数进行拟合。

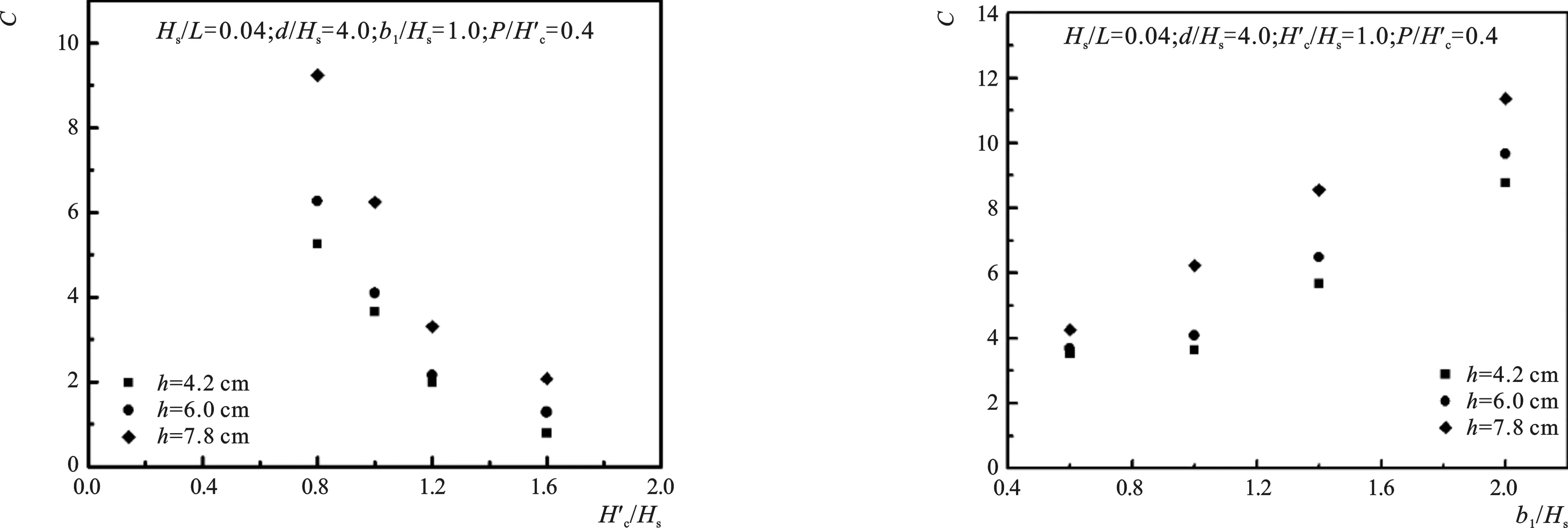
图8 C与H′c/Hs的关系Fig.8 Relational graph of C versus H′c/Hs图9 C与b1/Hs的关系Fig.9 Relational graph of C versus b1/Hs

3.6 h/Hs与C值的相关关系

该无因次表达式共计6个影响因素，调整h/Hs的值，控制其他影响因素不变时，C值试验结果如图11所示。从图中可以看出，C值随h/Hs增加而增加，采用指数函数进行拟合。

图10 C与P/H′c的关系Fig.10 Relational graph of C versus P/H′c图11 C与h/Hs的关系Fig.11 Relational graph of C versus h/Hs

3.7 扭王字护面块体惯性阻力系数C的计算关系式

根据3.1～3.6节单一变量分析结果，采用多元回归方法对惯性阻力系数C进行非线性拟合，给出坡度m=1.5时，扭王字块体护面斜坡堤C值的计算公式为

(2)

表4 惯性阻力系数的公式(2)计算值Tab.4 Formula calculated value of C

上式相关系数R>0.90，满足非线性拟合要求。经上述拟合公式计算，分别得到h=4.2 cm、h=6.0 cm和h=7.8 cm扭王字块体C值的公式(2)计算值，如表4所示。再应用表4中的公式计算值进行数模计算，得到相应45种工况下的胸墙水平波浪力值。相应的数模计算值与物模试验值对比结果如图12所示，两者具有较高的一致性，表明公式(2)具有较好的计算精度。

图12 采用公式(2)惯性阻力系数的胸墙波浪水平力数模值与物模值对比Fig.12 Comparison between numerical results and physical model results of horizontal wave force on breast wall

4 结论

(1)借助FLUENT软件，通过建立斜坡堤胸墙波浪水平力与惯性阻力系数关系曲线，并依据胸墙波浪水平力的物模试验值，确定不同工况下的惯性阻力系数，在此基础上运用非线性拟合分析，进而得到了惯性阻力系数的计算公式。由于惯性阻力系数的计算公式中，综合考虑了波陡、相对水深等水动力因素和相对块体尺寸、相对胸墙高度、相对堤顶超高、相对坡肩宽度等斜坡堤结构因素，使得该公式适用性较强。

(2)采用本文公式(2)计算的惯性阻力系数C值，扭王字块体护面斜坡堤胸墙受力的数模计算值与物模试验值吻合良好，表明本文应用的数值模拟方法合理且有效，创新开展了FLUENT软件模拟计算扭王字块体护面斜坡堤胸墙受力的方法，使得数值模拟扭王字块体护面斜坡堤胸墙受力成为一种无需依附于物模试验的独立的试验手段，为扭王字块体护面斜坡堤胸墙受力的深入研究开辟了一条新的途径。