超压强化TP2铜材抗拉强度的工程应用性研究
杨 帆 张 磊 陈 帆 陈 刚 张红卫 范有雄 刘小宁
(武汉软件工程职业学院 湖北 武汉:430205)
0 引言
铜材具有耐腐蚀、抗低温及传热性好的优点,在日常生活与工业生产中得到大量应用。例如,铜管可用于输送有一定压力的流体,耐腐蚀铜制压力容器、低温铜制压力容器与铜制换热器在工程实践中也得到一定应用[1-2]。我国铜贮藏量不足世界总贮藏量的10%,节约用铜是我国学术界与工程界值得探索的课题。
铜制承压设备(管道)的壁厚往往是由铜材的机械强度指标确定[1-2],其中,铜材的抗拉强度是机械强度的主要指标之一;在保证安全性的前提下,稳定地提高铜材的抗拉强度,就能减小铜制承压设备(管道)的壁厚,达到节约用铜。对于尺寸与材料等条件相同的铜制承压管道与设备,爆破压力大小是其材料抗拉强度的表征。基于奥氏体不锈钢容器室温与液氮温度下的应变强化研究[3-7],可认为9%预应变可提高其抗拉强度。对尺寸与材料等条件相同的软态TP2铜管,若其预处理压力不低于其屈服压力,试验表明[8],与非预处理铜管相比,预处理铜管的爆破压力得到提高,表明当铜管预处理压力不低于其屈服压力时,铜管的爆破压力得到提高,铜材的抗拉强度得到强化。超压强化TP2铜材抗拉强度的工程应用性,是指软态TP2铜材抗拉强度强化效果的工程实用性,从工程实用的角度,必须考虑如下几个方面的内容:①软态TP2铜抗拉强度的强化效果与预处理压力大小存在怎样的联系;②抗拉强度提高的强化效果在铜材贮存或者工作条件下的持久性[9-10];③常用的铜光管与铜内螺纹管这两种结构对强化效果是否存在影响[11-12]。
针对上述3个问题,文中以软态TP2铜管的抗拉强度为研究对象,在预处理压力分别为0、4.60MPa与16.50MPa时,基于强化铜管自然时效时间分别为0、半年、1年与2年的79个爆破压力试验数据,应用数理统计方法与概率论知识[13-22],研究了强化软态TP2铜材抗拉强度的工程应用性。
1 基本方法
1.1 随机变量的构建
虽然爆破压力是铜制承压设备(管道)强度的直观表征,但是,在其他条件相同时,爆破压力的大小与管道与设备的尺寸有关,而抗拉强度反映了材料强度的本质,其大小与尺寸无关,因此,文中将一定条件下的铜材抗拉强度视为随机变量。
铜制圆筒形设备(管道)的爆破压力计算公式为[1,12]
(1)
式中,R为铜材抗拉强度,MPa;p为圆筒形设备(管道)爆破压力,MPa;K为圆筒形设备(管道)的径比,K=Do/Di=1+2t/Do;Do,Di分别为圆筒形设备(管道)的外直径与内直径,mm;t为管道或容器的壁厚,mm。
当Do与t为已知时,式(1)的等价形式为[12]
(2)
1.2 总体与样本
随机变量的主要性质包括分布规律与参数[13-15],随机变量是总体,它由无数个符合一定条件的样本或者个体构成,虽然刻划随机变量这个总体的性质需要无数个符合一定条件的个体或者样本才能得到,但是,可以通过获得尽量多的有限个符合一定条件的个体或者样本,在一定置信度时,对刻划随机变量这个总体的性质进行估计或者预测。获得个体或者样本的方法可能有所不同,但是基本要求是满足与建立总体的条件相同。一方面,可以通过有限个样本或者个体对随机变量这个总体的性质进行估计,另一方面,可以通过随机变量这个总体的分布规律对样本或者个体的有效性与同质性进行分析。
样本的有效性是指条件相同时,样本必须与总体同时具有相同性质。样本的同质性是指两组条件不同的有效样本,能同时反映某一随机变量的性质,表明条件不同对性质的影响不大。有效性是选择样本的基础,而同质性是合并样本的前提。
在处理具体问题时,刻划随机变量这个总体的性质(包括分布规律与分布参数)都是未知的,从工程实践的角度,可以基于获得的与随机变量对应总体的有效样本,通过假设检验确定随机变量的分布规律,通过似然分析得到随机变量的分布参数的区间估计。当一定的条件发生变化时,随机变量的性质是否发生变化,必须通过获得个体或者样本进行检验,一般会出现如下3种情况:1)随机变量分布规律没有发生变化,而分布参数发生变化,表明随机变量分布规律对条件发生变化不敏感,而分布参数对条件发生变化敏感;2)随机变量分布规律与分布参数都没有发生变化,表明随机变量的性质对条件发生变化不敏感;3)随机变量分布规律与分布参数都发生变化,表明随机变量的性质对条件发生变化敏感。
1.3 两个随机变量分布参数的估计
每个符合正态分布随机变量分布参数包括3个,即均值、标准差与变异系数。为了研究强化TP2铜管抗拉强度分布规律与稳定性,假设A与B条件下,抗拉强度分别为RA与RB,且均符合正态分布,其均值、标准差与变异系数分别为μA和μB、σA和σB与CA和CB。
1.3.1 随机变量RA的分布参数
①样本的有效性及统计。在A条件,RAi(i=1,2,…,nA)为获得的nA组样本,其平均值与精密度分别为:
(3)
(4)
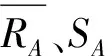
在双侧置信度为(1-0.5α)时,有效样本的判别指标
(5)
判据为
|tAi|≤t1-0.5α,nA-1
(6)
式中,t1-0.5α,nA-1为t分布系数,由单侧置信度(1-0.5α)与自由度(nA-1)与查得。文中所用t分布系数见表1[23]。

表1 分布系数
若样本RAi满足式(6),表示其为有效,如果不满足,则RAi为无效样本,需要删除后再重新统计。
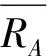
均值μA在双侧置信度为(1-α)时的估计区间为
μA∈[μAmin,μAmax]
(7)
其中
(8)
(9)
式中,μAmin与μAmax分别是单侧置信度为(1-0.5α)时RA均值μA的最小与最大值。
标准差σA在双侧置信度为(1-α)时的估计区间为
σA∈[σAmin,σAmax]
(10)
其中
(11)
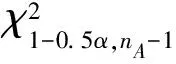
取α=0.05,文中所用的χ2分布系数见表1[24]。
变异系数CA在双侧置信度为(1-α)时的估计区间
CA∈[CAmin,CAmax]
(12)
其中
(13)
1.3.2 随机变量RB的分布参数
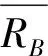
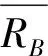
②随机变量分布参数估计。均值μB的估计区间。令式(7)~式(9)A→B,可得μB在双侧置信度为(1-α)时的最小值μBmin与最大值μBmax,μB的估计区间为
μB∈[μBmin,μBmax]
(14)
标准差σB的估计区间。令式(10)与式(11)中A→B,可得σB在双侧置信度为(1-α)时的最小值σBmin与最大值σBmax,σB的估计区间为
σB∈[σBmin,σBmax]
(15)
变异系数CB的估计区间。双侧置信度为(1-α)时,令式(12)与式(13)中A→B,可得CB的最小值CBmin与最大值CBmax,其估计区间为:
CB∈[CBmin,CBmax]
(16)
其中
(17)
随机变量样本的同质性及统计。如果样本RAi与RBi对应的随机变量RA与RB基本符合正态分布,当由样本RAi与RBi估计的分布参数标准差与均值分别无显著差异时,表明RA与RB相同,即可将样本RAi与RBi合并,用其估计同一随机变量的性质。
1.4 两个随机变量分布参数的比较
在双侧置信度为(1-α)时,可利用样本RAi与RBi的平均值和精密度,对两个随机变量RA与RB分布参数估计区间进行比较,如果分布参数的均值、标准差与变异系数分别无显著差异,表明随机变量RA与RB相同,即分布参数对条件变化无影响。
两个随机变量同一参数有显著差异是指其估计区间无共同部分,无显著差异是指其取值区间有共同部分,从其共同部分的关系可分析变化趋势;当条件从A变化为B时,同一参数的比较判据与结论见表2。
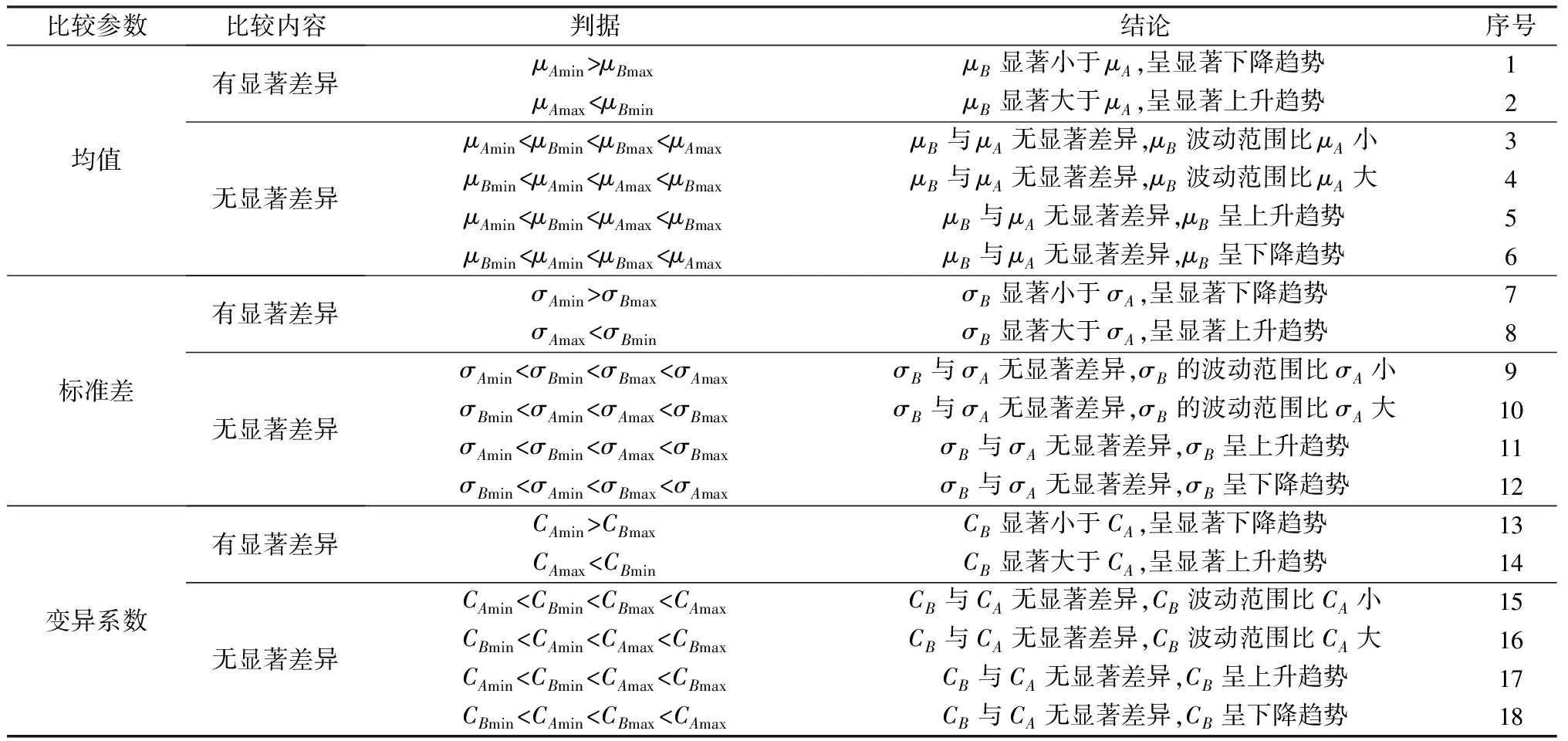
表2 条件变化时两个随机变量同一参数的比较判据
1.5 分布系数稳定性比较
分布参数稳定性是指波动范围的大小,波动范围小表明稳定性好。双侧置信度为(1-α)时,RA均值、标准差与变异系数的波动范围分别为
ΔμA=μAmax-μAmin
(18)
ΔσA=σAmax-σAmin
(19)
ΔCA=CAmax-CAmin
(20)
在式(18)~式(20)中令A→B,可得到随机变量RB均值、标准差与变异系数的波动范围。
稳定性好与差可采用分布参数波动范围的绝对值进行判别:比较均值、标准差与变异系数波动范围,波动范围小的绝对值表明对应参数的稳定性好。
2 试验数据与统计
2.1 试验数据及条件分类
对符号下标说明如下:A、B与D,分别对应预处理压力py为0、4.60MPa与16.50MPa,g与l分别对应铜光管与铜内螺纹管。在2年自然时效时间年,文献[8,11-12]提供了79个软态TP2铜管的爆破试验数据。
2.1.1 预处理压力与自然时效时间为零,铜管结构不同
文献[11]在预处理压力与自然时效时间为零时,基于有关企业与自测的爆破试验,提供了几何尺寸不同的13个铜光管与11个铜内螺纹管爆破压力的有效试验数据,见表3。
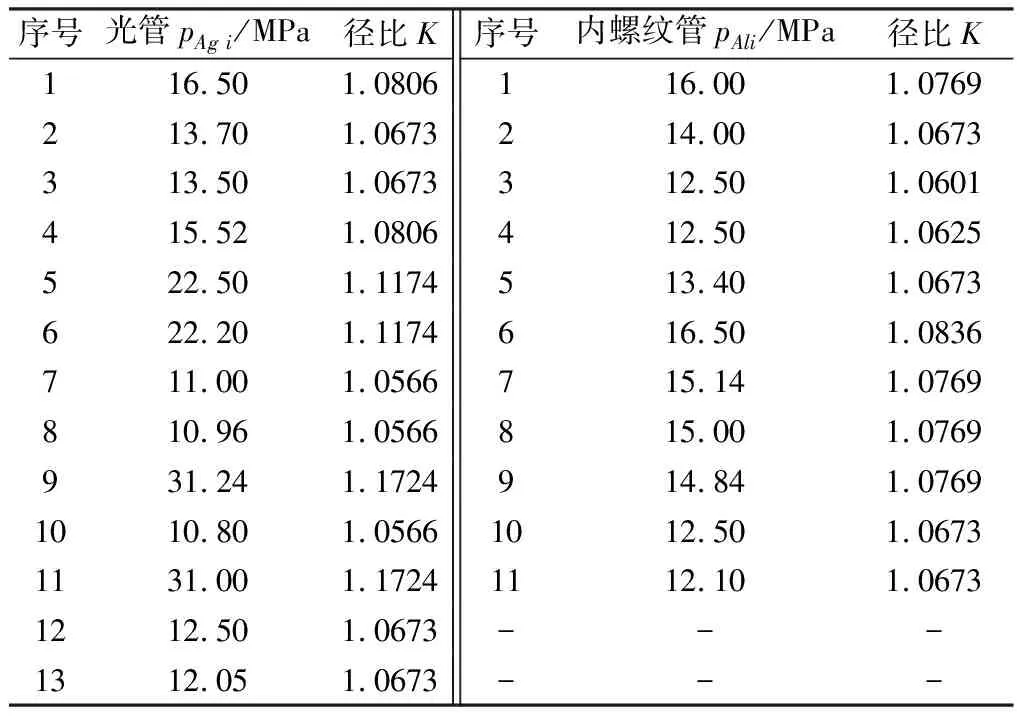
表3 预处理压力为零的铜管实测爆破压力试验数据[11]
根据式(1),将表3中爆破压力转换为相同条件下软态TP2铜材的抗拉强度,再按式(3)与式(4)得到统计数据,一并列入表4。

表4 预处理压力为零的软态TP2铜材抗拉强度统计
2.1.2 预处理压力、自然时效时间与铜管结构分别不同
爆破试验采用软态TP2铜制成的铜光管与铜内螺纹管,铜光管的原始尺寸为Φ9.52×0.30(外直径×壁厚),铜内螺纹管的原始尺寸为Φ9.52×0.30×0.20(外直径×壁厚×齿高);两种结构不同铜管的径比K均为1.0673。经过预处理的铜管放置于自然环境,在相应的自然时效时间进行爆破试验。经预处理的铜管已开始变形,因此,将铜管爆破压力转换为相同条件下软态TP2铜材抗拉强度计算中尺寸,采用的是铜管原始尺寸。
①当预处理压力为4.60MPa,自然时效时间为0时,文献[8]提供了3个铜光管与3个铜内螺纹管爆破压力试验数据;自然时效时间分别半年、1年与2年时,基于软态TP2铜管的爆破试验,本研究分别获得了3个铜光管与3个铜内螺纹管爆破压力试验数据,见表5。根据式(1)或(2),按铜管的原始尺寸,将爆破压力转换为相同条件下铜材的抗拉强度,列入表6。
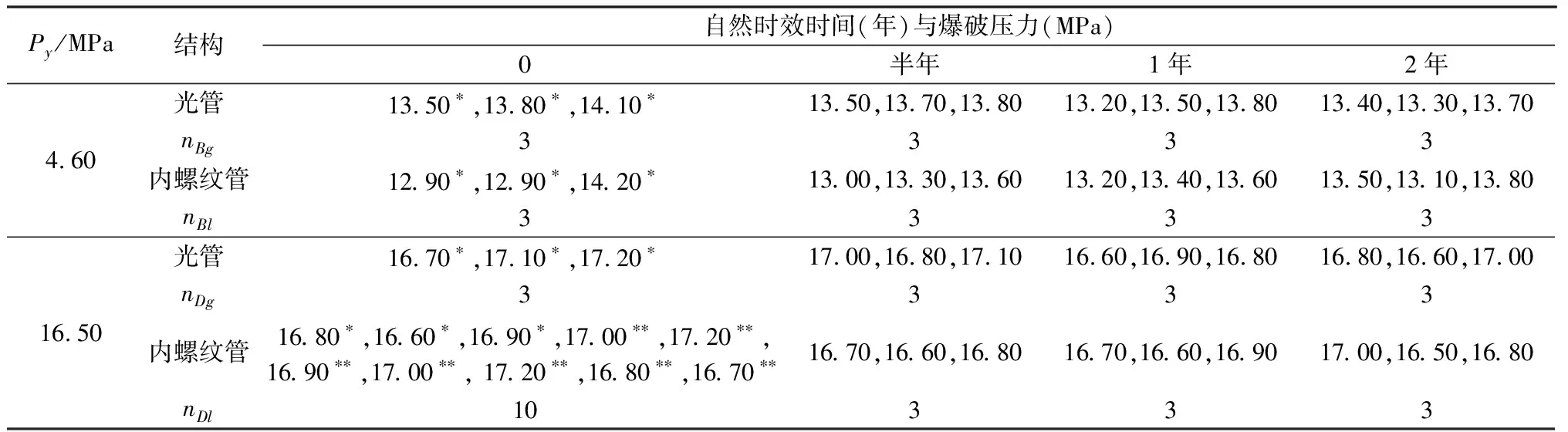
表5 不同预处理压力与自然时效时间时铜管爆破压力试验数据
②基于预处理压力为16.50MPa的软态TP2铜管爆破试验,自然时效时间为0时,文献[8,12]共提供了3个铜光管与10个铜内螺纹管爆破压力试验数据;在自然时效时间分别为半年、1年与2年时,根据本研究获得了3个铜光管与3个铜内螺纹管爆破压力试验数据,也列入表6。根据式(1)或式(2),按铜管的原始尺寸,将爆破压力转换为相同条件下软态TP2铜材的抗拉强度,一并列入表6。
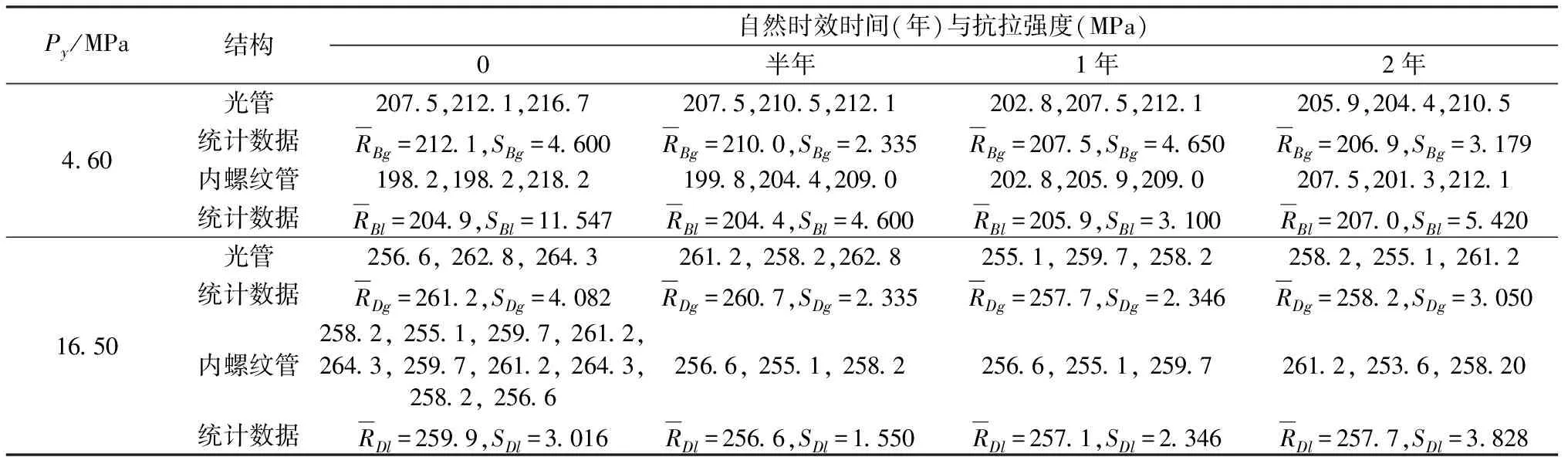
表6 不同预处理压力与自然时效时间时软态TP2铜材抗拉强度及统计
2.2 试验数据的有效性
在双侧置信度为95%时,分析软态TP2铜材抗拉强度的有效性。
2.2.1 预处理压力为0
对表4中由13个铜光管爆破压力得到的抗拉强度数据,按式(5)得到有效样本的判别指标tAi=-1.986~1.746,满足判据式(6):|tAgi|≤t0.975,12=2.179,表明由13个铜光管爆破压力得到的抗拉强度数据有效。
对表4中由11个铜内螺纹管爆破压力得到的抗拉强度数据,按式(5)得到有效样本的判别指标tAli=-1.993~1.253,满足判据式(6):|tAli|≤t0.975,10=2.228,表明由11个铜内螺纹管爆破压力得到的抗拉强度有效。
2.2.2 预处理压力为4.60MPa
当自然时效时间分别0、半年、1年与2年时,对表6中由3个铜光管爆破压力得到的抗拉强度数据,按式(5)得到样本的判别指标分别为tBgi=-1.000~1.000,-1.071~0.899,-1.011~0.989与-0.786~1.132;由3个铜内螺纹管爆破压力得到的抗拉强度数据,按式(5)得到样本的判别指标分别为tBli=-0.580~1.152,-1.000~1.000,-1.000~1.000与-1.052~0.941;判别指标均满足判据式(6):|tBgi|≤t0.975,2=4.303与|tBli|≤t0.975,2=4.303,表明由铜光管与铜内螺纹管爆破压力得到的抗拉强度数据均分别有效。
2.2.3 预处理压力为16.50MPa
当自然时效时间分别为0、半年、1年与2年时,对表6中由3个铜光管爆破压力得到的抗拉强度数据,按式(5)得到样本的判别指标分别为tDgi=-1.127~0.759,-1.071~0.899,-1.108~0.853与-1.016~0.984,满足判据式(6):|tDgi|≤t0.975,2=4.303,表明由铜光管爆破压力得到的抗拉强度数据分别有效。
当自然时效时间为0,对表6中由10个铜内螺纹管爆破压力得到的抗拉强度数据,按式(5)得到样本的判别指标为tDli=-1.592~1.459,满足判据式(6):|tDli|≤t0.975,9=2.262,表明由10个铜内螺纹管爆破压力得到的抗拉强度数据有效。
当自然时效时间分别为半年、1年与2年时,对表6中由3个铜内螺纹管爆破压力得到的抗拉强度数据,按式(5)得到样本的判别指标分别为tAi=-0.968~1.032,-0.853~1.108与-1.071~0.914,满足判据式(6):|tDli|≤t0.975,2=4.303表明在自然时效时间分别为半年、1年与2年时,由3个铜内螺纹管爆破压力得到的抗拉强度数据分别有效。
3 预处理压力与强化效果
假设预处理压力相同,相同自然时效时间的由相同结构铜管得到的铜材抗拉强度分别符合正态分布,根据表4与表6数据,按式(7)~式(13),可得到分布参数在双侧置信度为95%时的估计区间,见表7。
3.1 预处理压力、自然时效时间与管结构相同
预处理压力为0时,不同结构结构铜管的自然时效时间也为0,为分析相同自然时效时间时,铜管结构对数据同质性的影响,应从预处理压力比较大的开始,比较的思路是,先将自然时效时间为0的分布参数估计区间,与自然时效时间分别为半年、1年与2年时的分别比较,再将自然时效时间为半年的与自然时效时间分别为1年与2年时的比较,再将自然时效时间为1年的与自然时效时间分别为2年时的比较;如果相同结构铜管在任意两个自然时效时间的3个分布参数估计区间均存在重合,表明3个分布参数分别无显著差异,即在0~2年自然时效时间,相同结构铜管的强化效果持久性好,可将有关数据合并后重新进行分布参数区间估计;若3个分布参数估计区间有1个不重合,则表明分布参数存在显著差异,即自然时效时间对分布参数存在显著影响。
①对预处理压力为16.50MPa的铜光管,横向比较表7中铜光管铜材在自然时效时间分别在0、半年、1年与2年时的任意两个时间抗拉强度分布参数估计区间,可以发现任意两个自然时效时间的3个分布参数估计区间分别都有重合,表明其无显著差异,即由铜光管爆破压力得到的抗拉强度,在2年自然时效时间保持稳定,因此,对于铜光管而言,预处理效果的持久性好,可将其在2年自然时效时间的数据合并,进行分布参数的区间估计。
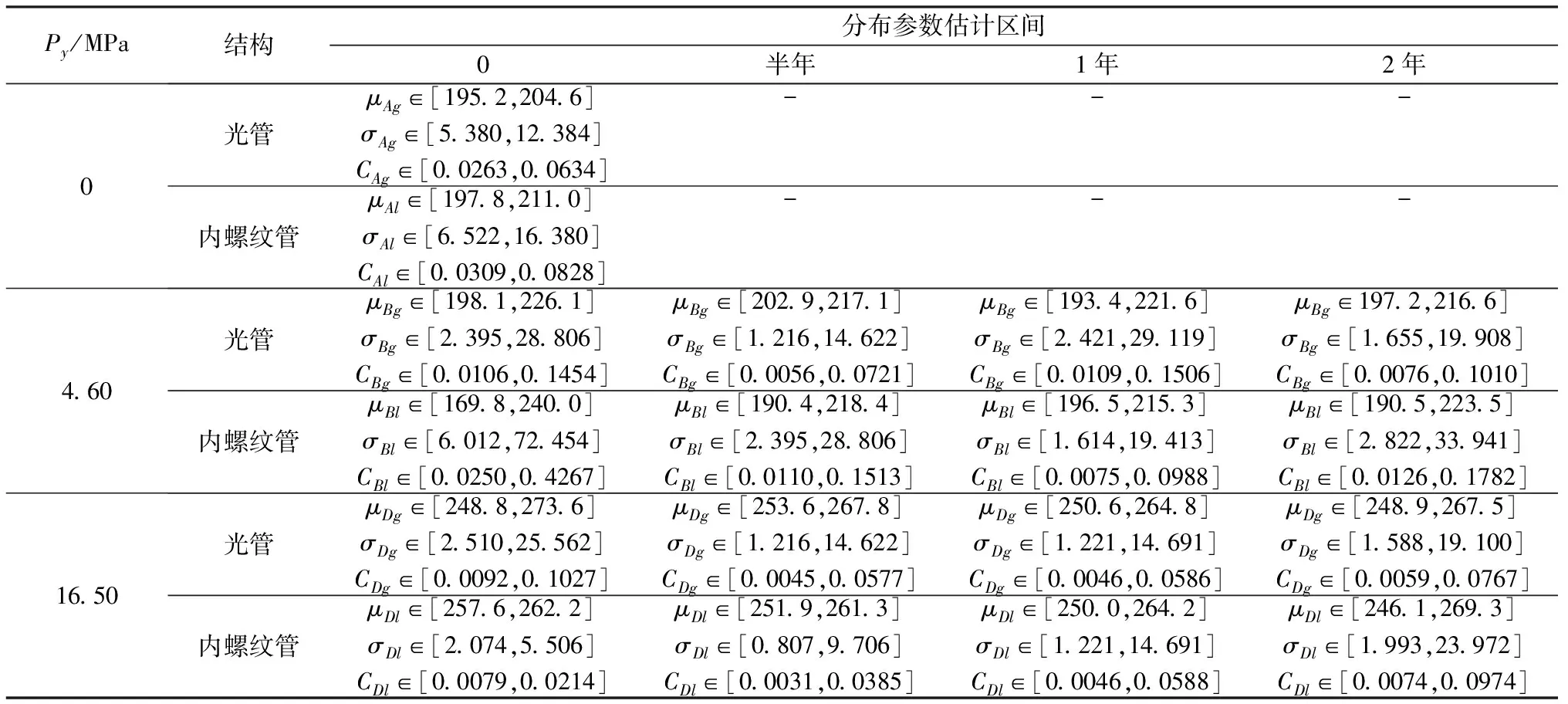
表7 不同预处理压力与自然时效时间时TP2铜材抗拉强度分布参数估计区间
对预处理压力为16.50MPa的铜内螺纹管,横向比较表7中光管铜材在自然时效时间分别为0、半年、1年与2年时的任意两个时间抗拉强度分布参数估计区间,可发现3个分布参数估计区间分别都有重合,表明其无显著差异,即由内螺纹管爆破压力得到的抗拉强度,在2年自然时效时间保持稳定,因此,对于内螺纹管而言,预处理效果的持久性好,将其在2年自然时效时间的数据合并,进行分布参数的区间估计。
②对预处理压力为4.60MPa的铜光管,横向比较表7中铜光管铜材在自然时效时间分别在0、半年、1年与2年时的任意两个时间抗拉强度分布参数估计区间,不难发现任意两个自然时效时间的3个分布参数估计区间分别都有重合,表明其无显著差异,即由铜光管爆破压力得到的抗拉强度,在2年自然时效时间保持稳定,因此,对于铜光管而言,预处理效果的持久性好,可将其在2年自然时效时间的数据合并,进行分布参数的区间估计。
对预处理压力为4.60MPa的铜内螺纹管,横向比较表7中铜内螺纹管铜材在自然时效时间分别在0、半年、1年与2年时的任意两个时间抗拉强度分布参数估计区间,也可发现3个分布参数估计区间分别都有重合,表明其无显著差异,即由铜内螺纹管爆破压力得到的抗拉强度,在2年自然时效时间保持稳定,因此,对于铜内螺纹管而言,预处理效果的持久性好,可将其在2年自然时效时间的数据合并,进行分布参数的区间估计。
根据以上分析,双侧置信度为95%时,如果预处理压力相同,由铜光管与铜内螺纹管获得的抗拉强度,在自然时效时间为2年时,其强化效果无显著差异,表明强化效果持久性好,可将铜光管与铜内螺纹管获得的抗拉强度分别合并,进行分布参数区间估计。
3.2 预处理压力、自然时效时间相同而管结构不同
①对预处理压力为16.50MPa的铜光管与铜内螺纹管,根据表7,在自然时效时间分别在0、半年、1年与2年时,分别比较铜材的分布参数估计区间,可发现3个分布参数估计区间分别存在重合,表明3个分布参数分别无显著差异。
②对预处理压力为4.60MPa的铜光管与铜内螺纹管,根据表7,在自然时效时间分别在0、半年、1年与2年时,比较铜材的分布参数估计区间,不难发现3个分布参数的估计区间分别存在重合,表明3个分布参数分别无显著差异。
③对预处理压力为0的铜光管与铜内螺纹管,根据表7,自然时效时间为0时,纵向比较铜材的分布参数估计区间,不难发现3个分布参数的估计区间分别存在重合,表明3个分布参数分别无显著差异。
根据以上分析,双侧置信度为95%时,如果预处理压力相同,由铜光管与铜内螺纹管获得的抗拉强度,在自然时效时间为2年时,其强化效果基本相同,可将铜光管与铜内螺纹管获得的抗拉强度合并,进行相同预处理压力铜材抗拉强度分布参数区间估计。
综上所叙,在相同预处理压力,2年自然时效时间,由铜光管与内螺纹管获得的抗拉强度具有同质性,可将相同预处理压力且2年自然时效时间的铜光管与铜内螺纹管试验数据合并,估计抗拉强度分布参数区间。
3.3 预处理压力不同
将表3与表6中相同预处理压力且2年自然时效时间内的铜光管与铜内螺纹管试验数据合并统计,得到表8,然后根据式(7)~式(13),可得到分布参数在双侧置信度为95%时的估计区间,也列入表8。
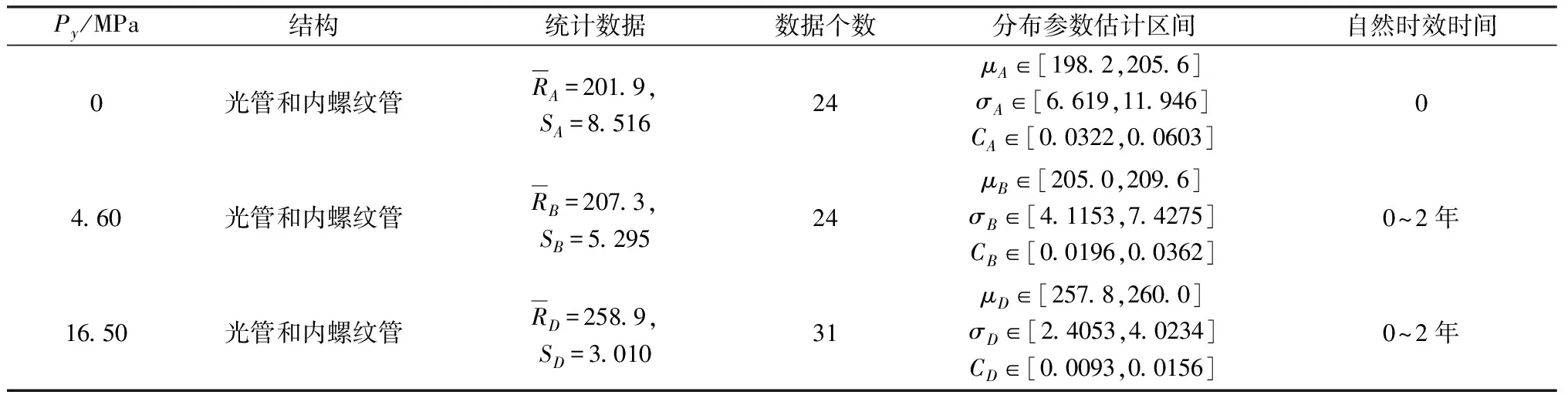
表8 不同预处理压力的TP2铜材抗拉强度统计与分布参数估计区间
根据表2判据比较表8数据可知:
①当预处理压力由4.60MPa增至16.50MPa,由表8可知,两个均值估计区间满足表2第2个判据:μBmax<μDmin,表明均值μB呈显著增大趋势;两个标准差估计区间也满足表2第7个判据:σBmin>σDmax,表明标准差σB呈显著降低趋势;两个变异系数估计区间满足表2第13个判据:CBmin>CDmax,表明变异系数CB呈显著降低趋势。
②当预处理压力由0增至16.50MPa,由表7可知,两个均值估计区间满足表2第2个判据:μAmax<μDmin,表明均值μD呈显著增大趋势;两个标准差估计区间满足表2第7个判据:σAmin>σDmax,表明标准差σD呈显著降低趋势;两个变异系数估计区间满足表2第13个判据:CAmin>CDmax,变异系数CD呈显著降低趋势。
以上分析表明,如果预处理压力足够大,预处理压力会引起抗拉强度分布参数发生显著变化,均值呈显著上升,标准差与变异系数呈显著下降。
③当预处理压力由0增至4.60MPa,由表8可知,两个均值估计区间满足表2第5个判据:μAmin<μBmin<μAmax<μBmax,表明均值μB呈无显著差异的上升趋势;两个标准差估计区间满足表2第12个判据:σBmin<σAmin<σBmax<σAmax,表明标准差σB呈无显著差异的下降趋势;两个变异系数估计区间满足表2第18个判据:CBmin 值得注意的是,预处理压力4.60MPa为试验铜管Φ9.52×0.30或者Φ9.52×0.30×0.20的屈服压力,表明采用屈服压力作为预处理压力,可使铜材抗拉强度得到一定程度强化。 综合以上分析,若预处理压力足够大,预处理压力引起抗拉强度分布参数发生显著变化,均值呈显著上升,标准差与变异系数呈显著下降。若预处理压力不低于铜管屈服应力,也可使铜材的抗拉强度得到强化,均值呈上升趋势,标准差与变异系数呈下降趋势。 将表8数据代入式(18)~(20),得不同预处理压力时抗拉强度分布参数稳定性的比较判据,见表9。 由表9可知,随着预处理压力由0增加到4.60MPa,再增加到16.50MPa时,软态TP2铜材抗拉强度分布参数的波动范围越来越小,表示分布参数越来越稳定。 表9 不同预处理压力时抗拉强度分布参数的波动范围比较 假设不同预处理压力时软态TP2铜材抗拉强度符合正态分布,是上面分析与讨论的基础;软态TP2铜材抗拉强度是否符合正态分布,还需要检验。 4.1.1 预处理压力分别为0与4.60MPa时 表10 不同预处理压力时TP2铜材抗拉强度的皮尔逊统计量 4.1.2 预处理压力为16.50MPa时 假设预处理压力为16.50MPa时,软态TP2铜材抗拉强度符合正态分布;由于1+3.3log31=5.9,故先将样本分为6个组,然后将其中的第1与第2组合并为1个组,重新构成5个组[13,18],每组样本的实际频数、理论概率、理论频数、实际频数与理论频数差异的的皮尔逊统计量之和,也列入表10中。 由表10可知,每个区间实际频数与理论频数差异的皮尔逊统计量之和为4.720,小于临界值5.991,表明在显著度为0.05时,软态TP2铜材抗拉强度基本符合正态分布,假设成立。 预处理压力分别为0、4.60MPa与16.50MPa时,软态TP2铜材抗拉强度基本符合正态分布,分布参数的估计区间见表8。显然,在其他条件相同时,分布参数的估计区间与预处理压力大小显著相关。 基于不同预处理压力软态TP2铜管在2年自然时效时间内的79个爆破压力试验数据,应用数理统计知识与概率论,在双侧置信度为0.95时,分析了不同条件时超压强化TP2铜材抗拉强度的有效性与同质性,讨论了抗拉强度的工程应用性,得到如下结论。 ①自然时效时间不超过2年,将铜管预处理压力从0增至4.60MPa,软态TP2铜材抗拉强度得到一定程度强化,均值呈上升趋势,标准差与变异系数呈下降趋势,分布参数波动范围逐步变小;将铜管预处理压力从4.60MPa增至16.50MPa,软态TP2铜材抗拉强度得到明显强化,分布参数发生显著变化,均值呈显著上升趋势,标准差与变异系数呈显著下降趋势,且分布参数波动范围明显变小趋于稳定,表明强化效果明显且在自然时效时间不超过2年时能持久保持。 ②当预处理压力分别为0、4.60MPa与16.50MPa,且自然时效时间不超过2年,可认为自然时效时间、铜光管与铜内螺纹管的结构对软态TP2铜材抗拉强度强化效果无显著影响,即强化效果没有受到自然时效时间和铜管结构的明显影响。 ③显著度为0.05,当预处理压力分别为0、4.60MPa与16.50MPa,且自然时效时间不超过2年,强化软态TP2铜材抗拉强度基本符合正态分布,分布参数与不同预处理压力有关,分别得到3种不同预处理压力时,强化TP2铜材抗拉强度分布参数的估计区间。 ④合适的预处理压力是强化软态TP2铜管有效方法,能显著提高强化软态TP2铜材的抗拉强度,显著降低其分布参数波动范围,可用于工程实践。3.4 不同预处理压力时抗拉强度分布参数的稳定性

4 抗拉强度的分布规律与分布参数
4.1 分布规律
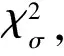
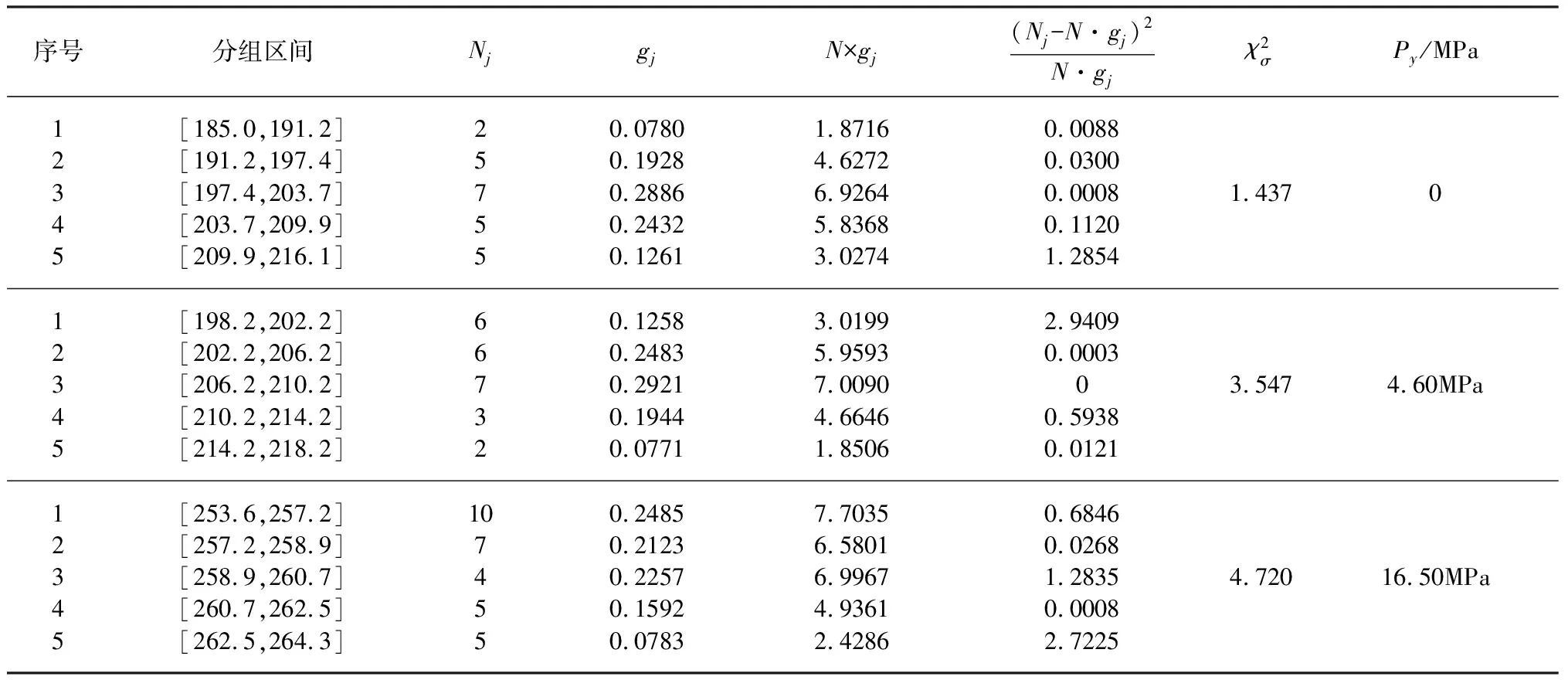
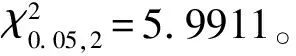
4.2 分布参数
5 结语

