一种Petri网最优控制序列的高效设计方法
邹岷强,马子玥
(西安电子科技大学 机电工程学院,陕西 西安 710071)
在现代柔性可重构自动控制系统中[1-4],系统需要在多个生产模式之间进行切换。由于模式切换往往需要系统处在某些特定的安全状态下才能进行,因此在收到指令时,相应的控制器会被激活并接管系统,并通过执行一组控制序列将系统驱动至安全状态以进行模式切换。通常情况下,系统中事件的执行会产生一定的成本(例如物料或时间的消耗等),因此人们往往期望能够使用低成本的控制序列实现系统状态的切换。在所有合法的控制序列中,成本最低的序列被称为“最优控制序列”。近些年来,如何高效在线计算最优控制序列得到了人们的广泛关注[5-6]。
Petri网作为离散事件系统的基本模型之一,已经被用于包括柔性制造系统、无人仓储、航电控制系统等各类可重构自动控制系统的建模与分析[1-15]。因此,近年来人们对Petri网中的控制序列设计问题进行了广泛研究[5-10],提出了许多设计最优控制序列的方法,例如广泛使用的模型预测控制[7]的搜索算法等。但是,此类搜索算法都是基于Petri网可达空间的穷举搜索,因此不可避免地遇到状态爆炸问题,使其在线计算效率低。另一方面,部分研究者提出的一些贪婪算法[8]和整数规划[9-11]虽然计算速度较快,但是其得到的控制序列不能保证最优,或是在线计算复杂度较高,往往不适用于实际情况。
近年来,CABASINO等[16]和MA等[17]提出了一种利用基本标识来对Petri网可达空间进行无损压缩的方法,从而避免对状态空间进行穷举,大幅减少了计算量。通过将基本标识分析方法和Dijkstra搜索算法[18]相结合,笔者提出一种高效求解Petri网最优控制序列的方法。算法将Dijkstra搜索的范围限定在被控网的基本标识空间中,从而在很大程度上缓解了穷举可达空间带来的状态爆炸问题。同时,通过选择合适的显式变迁集合来构建基本标识空间,使得搜索过程中无需求解整数规划。该算法具有在线计算量小、求解速度快的优点,适用于受控系统需要对重构请求作出快速响应的场合。
1 基本定义
文中的Petri网由四元组N=(P,T,Pre,Post)表示。其中P为m个库所的集合{p1,…,pm},T为n个变迁的集合{t1,…,tn}。Pre与Post为N的输入矩阵与输出矩阵,分别为m行n列的非负整数矩阵。Petri网N的关联矩阵定义为C=Post-Pre。
给定Petri网N=(P,T,Pre,Post),其标识M是一个m维的非负整数向量。若对于某一变迁t∈T,标识M满足M≥Pre(·,t),则称变迁t在标识M下使能,记作M[t>。使能的变迁t在M下可以发射,记作M[t>M′,其中M′是系统经变迁t发射后到达的标识,其满足状态方程M′=M+Post(·,t) - Pre(·,t)=M+C(·,t)。对于一组标识M、M′,若存在一组变迁序列σ=t1t2…tn,满足M[t1>M1,M1[t2>M2,…,Mk-1[tk>M′,则称标识M′从标识M可达,记作M[σ>M′,σ=t1t2…tn。用〈N,M0〉表示带有初始标识M0的Petri网N,称为初始化的网系统。〈N,M0〉的可达空间定义为所有从M0可达的标识组成的集合,记为R(N,M0)。
文中用T*表示T上所有由变迁组成的有限长度序列的集合,其上标*为Kleene星号运算符。
2 基本标识空间
定义1给定Petri网N,其变迁集合为T。若T的两个子集TE和TI满足(1)T=TE∪TI,TE∩TI=φ,且(2)TI导出的子网无环,则称TE、TI为网变迁集合T的一个基本划分,记为(TE,TI)。TE和TI分别称为显式变迁集合和隐式变迁集合。
定义2给定标识M和一个显式变迁t∈TE:
(2) 给定Σ(M,t)时,定义Y(M,t)={yσ|σ∈Σ(M,t)},为t在标识M下的解释向量集合;
(3) 给定Y(M,t)时,定义Ymin(M,t)=minY(M,t),为t在标识M下的最小解释向量集合。
定义3给定Petri网〈N,M0〉和其变迁的一个基本划分(TE,TI),其基本标识空间Mbasis递归定义为:① 初始标识M0∈Mbasis;② 若M∈Mbasis,则对所有t∈TE,所有y∈Ymin(M,t),M′=M+C·y+C(·,t)∈Mbasis。
定义4给定Petri网〈N,M0〉和其变迁的基本划分(TE,TI)。标识M的隐可达标识集合定义为
RI(M)={M′|M[t1t2…tn>M′,t1,t2,…,tn∈TI} 。
定理1若Petri网中M0[σ>M,则存在一组基本标识M0-M1- … -Mn且M∈RI(Mn)。
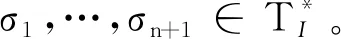
M0[σ1t1>M1[σ2t2>M2…Mn-1[σntn>Mn[σn+1>M,
其中,M0是基本标识。由于隐式变迁导出的子网无环,根据文献[15]中定理3,如果σ1所对应的发射向量y1不是M0下t1的最小解释向量,则一定可以将σ1拆分为两部分σ1′、σ1″,满足M0[σ1′t1>M1′[σ1″σ2t2>M2,且σ1′所对应的发射向量是M0下t1的最小解释向量。那么前式可改写为
M0[σ1′t1>M1′[σ1″σ2t2>M2…Mn-1[σntn>Mn[σn+1>M,
其中,M1′是基本标识。将M1′视为新的初始标识,可以反复应用上述变迁拆分重排规则,最终得到发射序列:
其中,M0,M1′,…,Mn′都是基本标识。因此M∈RI(Mn′),定理成立。
根据定理1,无论如何选择显式变迁集合和隐式变迁集合,所有基本标识均可由初始标识到达,即满足Mbasis⊆R(N,M0),基本标识集合一定是可达集合的子集。文献[15-17]中的大量仿真结果表明,在合理选择显式变迁集合TE的情况下,一般有|Mbasis|≪|R(N,M0)|,即基本标识集合的规模远远小于可达集合。
3 最优控制序列设计
在Petri网的最优控制序列设计问题中,控制器需要计算出一个称为“控制序列”的变迁序列,使得系统在源标识Ms下执行该控制序列可以到达某个属于目标标识集合Mtarget的标识。在现实情况下,执行控制序列的目标通常是为了将部分子系统的局部资源清空,从而对其进行重构。这种情况下,期望的目标标识可由包含“≤”的不等式进行描述。因此,为了简化问题,笔者考虑系统目标标识集合Mtarget由广义互斥约束描述的情况。
假设1系统中的目标标识由一组广义互斥约束[19](w,k)表示,即Mtarget={M|wTM≤k}。
定义5给定Petri网〈N,M0〉,N=(P,T,Pre,Post)。令Ms∈R(N,M0)为源标识,Mtarget为目标标识集合,若满足Ms[σ>M∈Mtarget,则称该控制序列σ合法。合法控制序列的集合记作П(Ms,Mtarget)。
为了快速响应控制需求,人们希望设计出有效算法,能够高效地计算得到所需的合法控制序列。同时,变迁的发射存在一定成本,例如执行相应事件时发生的材料或时间的消耗。因此,人们希望得到的控制序列总成本(即该序列所包含的所有变迁的成本之和)尽可能低。
定义6定义成本向量c=[c(t1),…,c(tn)]T≥ 0,为n维实数向量,其中c(t)为变迁t的单次发射成本。控制序列σ的发射成本定义为cTyσ。
定义7给定Petri网〈N,M0〉,成本向量c,源标识Ms∈R(N,M0),目标标识集合Mtarget=S(w,k),若控制序列σ∈П(Ms,Mtarget)的成本cTyσ最小,则称其为最优控制序列,用σmin表示。
注意到定理1虽然保证了M必然属于某个基本标识Mn′的隐式可达标识,但是满足M∈RI(Mn′)的基本标识Mn′(可能不惟一)并不能预先求得。因此,需要对基本标识集合Mbasis中的每一个基本标识都进行一次判断。
在文献[17]中,通过求解整数线性规划来判断相应的隐式变迁序列是否存在,因此需要求解大量的整数规划问题,其实际计算效果并不理想。为规避整数线性规划的求解,此处笔者提出一个关于选择显式变迁集合的条件。在该条件下,M∈RI(Mn′)的判定可以通过代数方法简单计算完成,无需求解整数规划问题。
定理2给定初始标识为M0的Petri网N,成本向量c,源标识Ms∈R(N,M0),目标标识集合Mtarget=S(w,k)。若П(Ms,Mtarget)不是空集且变迁基本划分(TE,TI)满足:对所有隐式变迁t,满足wTC(·,t)≥0,则一定存在一个最优控制序列σmin=σ1t1σ2t2…σntn,满足:Ms[σ1t1>M1[σ2t2>M2,…,Mn-1[σntn>Mn∈Mtarget,其中,Ms,M1,…,Mn均为基本标识。
证明:假设σ∈П(Ms,Mtarget),为一个最优控制序列,则有cTyσ=cmin。根据定理1,可以将σ中的变迁进行重新排列,得到序列σ′=σ1t1σ2t2…σntnσn+1∈П(Ms,Mtarget),使得Ms[σ1t1>M1[σ2t2>M2…Mn-1[σntn>Mn[σn+1>Mt∈Mtarget。其中,Ms,M1,…,Mn均为基本标识。由于序列σ′是由σ调整变迁顺序得到,因此cTyσ′=cmin,即σ也是一个最优控制序列。由于Mt∈Mtarget意味着wTMt≤k,且所有隐式变迁t均满足wTC(·,t) ≥ 0,因此wTMn≤wTMt≤k,即Mn∈Mtarget。由于变迁的发射成本均非负,因此从序列σ′中删去最后一段σn+1,得到的序列σ″=σ1t1σ2t2…σntn,也是合法的控制序列,且cTyσ″≤cTyσ′。由于cTyσ′已经是最小,等号必然成立,即cTyσ″=cmin。这表明σ″=σ1t1σ2t2…σntn是一个最优控制序列,定理得证。
定理2表明,若选择基本划分确保所有满足wTC(·,t)≥0的变迁t都属于隐式变迁集合TI(等价地,所有满足wTC(·,t)<0的变迁t都属于显式变迁集合TE),且合法控制序列集合不为空,则始终存在一个以显式变迁结束的最优控制序列。因此,在从Ms到Mn的每一步搜索中,都不需要通过求解整数规划来验证基本标识Mi是否可以通过发射隐式变迁到达Mtarget,而只需要验证Mi自身是否属于Mtarget即可。根据假设1,这一条件可以通过检查Mi是否满足wTM≤k来直接验证。在此情况下,无需求解整数规划问题即可快速确定目标集合的隐式可达性。
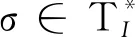
算法1Petri网最优控制序列设计。
输入:Petri网〈N,M0〉,N=(P,T,Pre,Post),成本向量c,源标识Ms,目标标识集合Mtarget=S(w,k)。
输出:一个最优控制序列σ。
① 选择一个满足条件的显式变迁集合;
② 初始化π={v0}其中v0=(Ms,0,Φ,Φ,Φ)并将其标记为new;
③ 令cmin=∞,vmin=v0;
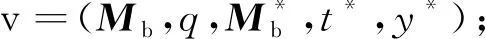
⑤ 对所有显式变迁t∈TE求解出其对应的Ymin(M,t);
⑥ 对Ymin(M,t)中的各个最小解释向量y:
⑦ 令Mb′=Mb+Cy+C(·,t);
⑧ 令q′=q+cTy+c(t);
⑨ 令v′=(Mb′,q′,Mb,t,y);
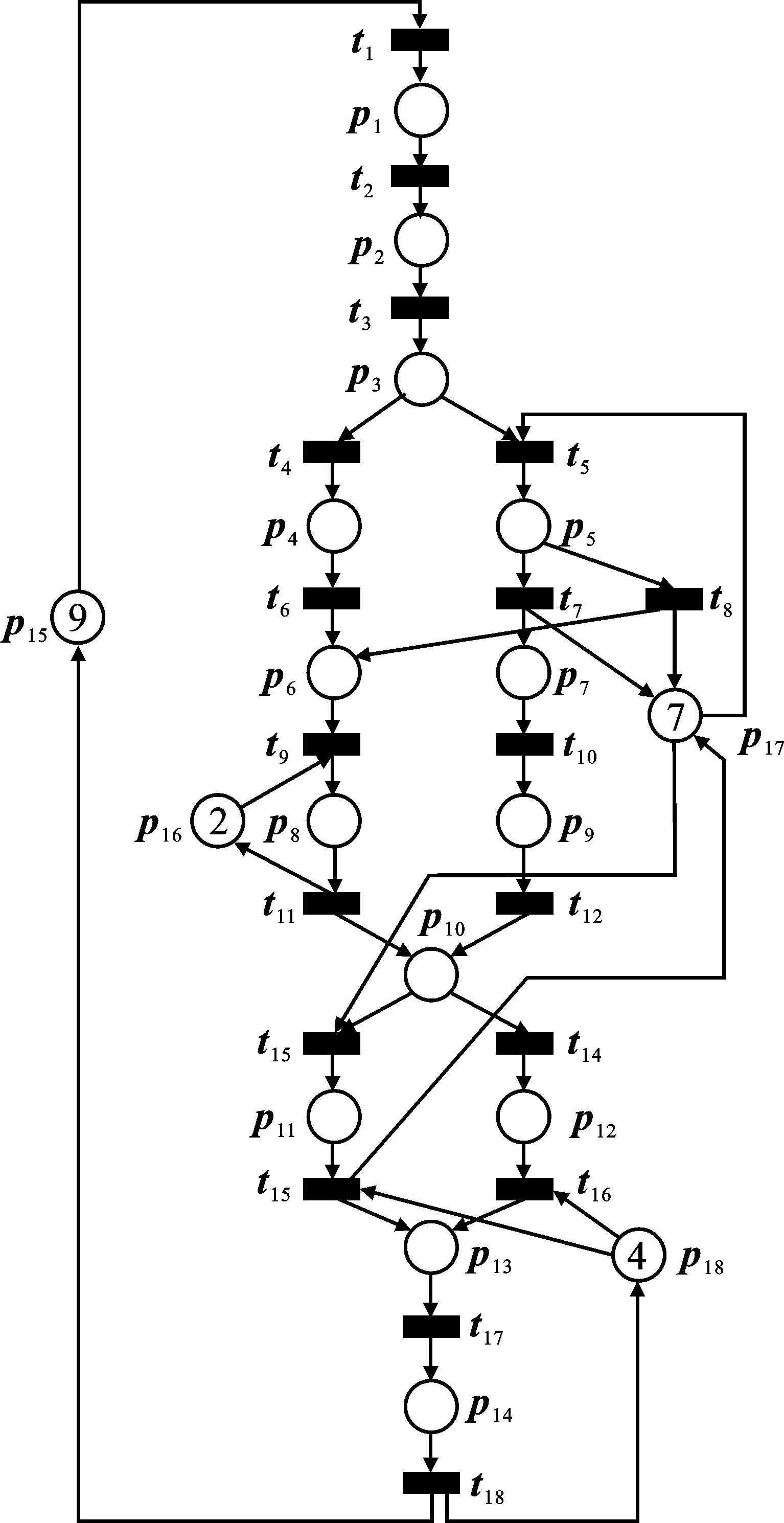
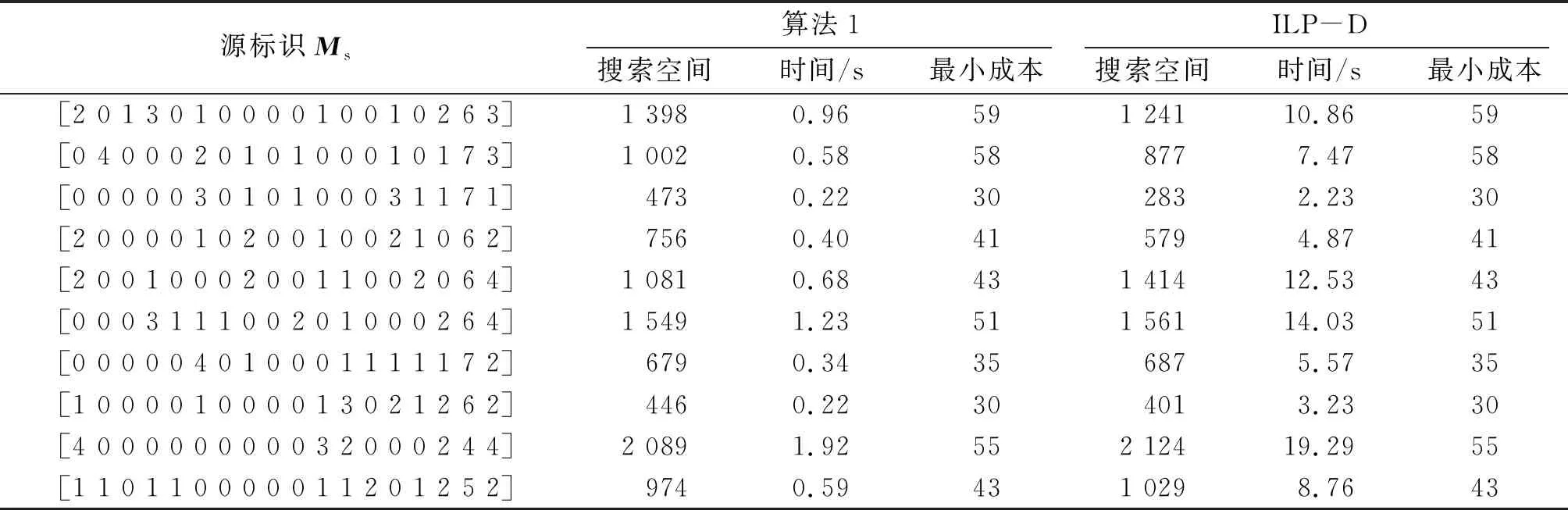
⑩ 若q′ 算法1将从Ms开始逐步探索基本标识空间,对每个已知结点Mi(即基本标识Mi)赋以非负实数D(i)以记录从源结点Ms到该结点的当前已知最短路径长度,称为Ms到Mi的“距离”。在每次迭代时,选择最接近源结点的未经检查的结点(即D(i)值最小的结点)进行下一步检查,并更新该结点的后继结点的距离D(j),称为“松弛”。算法1的复杂度为|Mbasis||T|,即其时间复杂度与基本标识空间的大小与变迁的数量分别呈线性关系。 定理3算法1输出的控制序列σ为最优控制序列。 考虑图1所示的智能制造系统。其中生产线I:p1t2p2t3p3负责对待加工产品进行预处理,生产线II:p4t6p6t9p8和生产线III:p5t7p7t10p9分别负责生产半成品A和B,经p10集散分配后分别发往p11和p12进行产品所需的表面工艺处理,之后经过p13t17p14进行组装得到成品,成品校验合格后进入库房。库所p15的容量为9,即整个系统能容纳的最大产品数量为9。 图1 智能制造系统Petri网模型 该系统的初始标识为M0= 9p15+2p16+7p17+4p18,即此时系统中各生产线处于空闲状态。假设系统已经运转了一段时间,现突发故障,需执行紧急重启,必须在系统关闭之前尽快从生产线上卸下所有正在加工的产品,即目标标识集合Mtarget={M|M(p15)≥ 9}。为简化问题,这里假定所有变迁的发射成本相等。 为了模拟上述调度问题,从系统的可达空间中随机选取10组标识作为调度源标识,代表系统在运行了一段时间后所处的状态。实验程序基于Python 3.7.6编写,在一台配备Intel Core i7-10750H 2.60/2.59 GHz CPU,16 GB RAM的笔记本上进行,使用的整数规划求解器为Gurobi Optimizer 9.0.3学术版。分别使用算法1和基于整数线性规划的Dijkstra方法(ILP-D)进行求解,仿真结果如表1。其中,ILP-D方法是基于文献[17]中的整数规划求解方法,选取显示变迁集合TE={t5,t11,t15,t17}。算法1考虑了显式变迁集合的选择条件,将满足wTC(·,t) < 0的变迁加入,选取TE={t5,t11,t15,t18}。 由表1中的结果可知: 表1 不同源标识下算法1与ILP-D方法的求解结果对比 (1) 在控制序列成本方面,算法1求解得到的控制序列成本与基于文献[17]的ILP-D方法求解得到的结果一致,表明算法1得到的控制序列成本是最小的,印证了算法1的正确性。 (2) 在算法的搜索空间方面,算法1与ILP-D方法求解得到的搜索空间大小相仿,其中搜索空间最大约2 000个标识。这一搜索空间规模远小于系统的可达空间规模(该系统的可达标识数为763 428)。这是由于上述两种算法均在基本标识空间内进行Dijkstra搜索,而基本标识空间通常比相应的可达空间小很多。因此与传统方法在可达空间中进行穷举相比,算法1能够有效地缓解状态爆炸问题。 (3) 从求解时间上看,针对同一源标识求解最优控制序列时,算法1所需的求解时间仅是ILP-D方法的10%甚至更低。这是由于算法1结合文中所述的基本标识分析(定理2)合适地选取了显式变迁集合,使得无需求解整数规划即可快速确定目标集合的隐式可达性,从而规避了繁复的整数规划求解问题。因此,与文献[17]中方法需反复求解整数规划问题相比,算法1具有更低的计算复杂性与更高的求解效率。 笔者提出了一种基于基本标识分析的Petri网最优控制序列设计算法。该算法在Petri网的基本标识空间中进行Dijkstra搜索,可有效地缓解传统方法穷举完整状态空间导致的状态爆炸问题。同时,笔者还提出了一种变迁选取规则,通过选择符合要求的显式变迁集合,使得无需求解整数规划即可快速确定目标集合的隐式可达性,规避了繁复的整数规划求解。与基于整数规划的Dijkstra方法相比,笔者提出的方法在线计算量小、求解速度快,效率得到显著提升。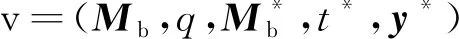
4 算 例
5 结束语

