协作干扰时频同步误差对安全通信性能影响

肖尚辉，陈燕铭，王梓豫，郭文博，邵士海

(1.电子科技大学 通信抗干扰技术国家级重点实验室，四川 成都 611731；2.成都工业学院 电子工程学院，四川 成都 610031)

随着无线通信技术的蓬勃发展，无线通信安全问题引起人们的广泛关注。为了实现可靠保密通信，现有设备常采用基于网络层密钥加密的信息安全技术。然而量子计算机的出现，使得现有解密算力呈指数级提升，给传统网络层加密技术带来了严峻的挑战[1]。物理层安全技术作为更有效、更具应用潜力的新安全技术应运而生，其核心是利用无线信道的广播特性和叠加特性，实现无线介质上信息可靠传输，且无须借助加密密钥。由于物理层安全技术与网络层加密技术相互独立，可以借助物理层安全技术来增强现有的网络层安全措施，从多个维度提高无线通信的安全性[2]。

协作干扰是实现物理层安全通信的重要手段，其核心思想是通过增添协作干扰信号来降低非授权窃听用户的信噪比，以提高系统通信安全性[3-4]。如图1所示，窃听节点E在获取来自发送节点S的信号同时，收到来自协作干扰节点J的干扰信号影响，恶化了接收信噪比。接收节点R也会接收到协作干扰信号，但利用协作干扰信号的先验信息，R可以消除协作干扰影响[5]。

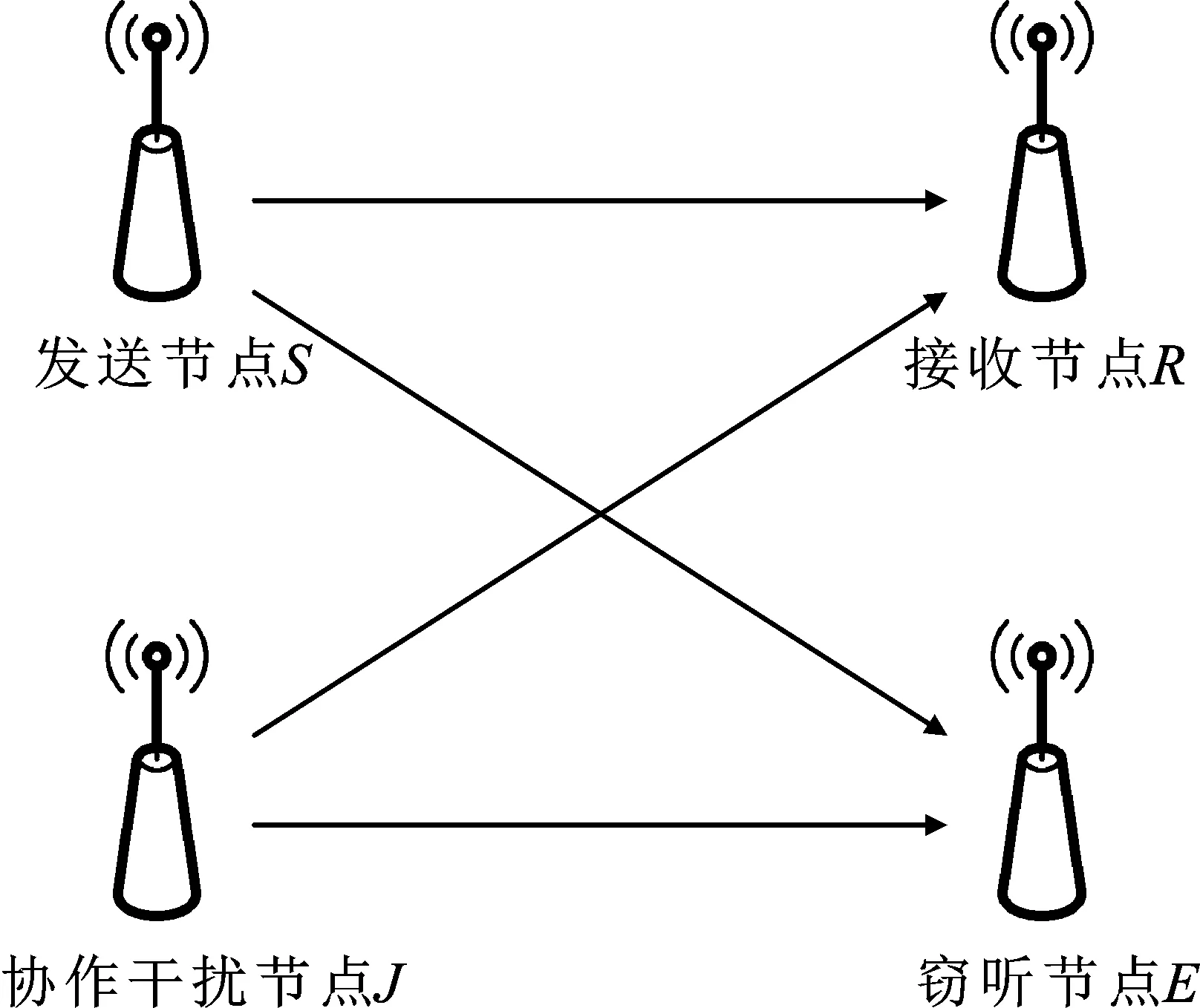
图1 协作干扰下安全通信示意图

目前研究人员对物理层协作干扰技术进行了相关探究。文献[6]设计了一种全双工干扰中继方案，窃听用户同时从源节点和中继节点接收相互干扰信号，有效地降低了窃听容量，从而提升了系统的保密性能。文献[7]考虑到传统协作干扰持续发送干扰信号带来的能量浪费和过度干扰问题，设计了一种间歇性干扰策略，实现了联合安全需求和干扰功率优化的目标。文献[8]采用反向传播神经网络对信道估计误差进行模拟和计算，并推导了最大保密率下信息侦听信号和人工噪声信号之间的最佳功率分配比。文献[9]针对协作干扰通信中的频率偏移和功率放大器非线性失真，提出了一种非线性自干扰消除方案，扩展了发射功率范围以提供更好的安全通信性能。

在授权接收机对协作干扰进行精准重建和对消是实现安全通信的前提，但现有研究工作均假定协作干扰在理想时间和频率同步下实现完美对消。由于硬件和传播环境的影响，且受实际工程时频同步精度的制约，尽管可以通过优化时频同步算法来降低同步误差，但始终存在残余误差，理想时间和频率同步是不可实现的[10-11]。针对这一问题，笔者研究了协作干扰时频同步误差对安全通信性能的影响，为设计实用安全通信系统提供理论支持。

针对上述问题，基于高斯窃听信道模型，笔者从理论上分析了协作干扰信号时频同步误差对授权用户安全通信性能的影响，并进行了仿真验证。首先，在高斯窃听信道模型下，得到了干扰抑制后的残余干扰功率表达式；然后推导了干扰抑制比、解调误码率、保密容量的闭合表达式；最后进行了计算机仿真验证。

1 系统模型

笔者采用的协作干扰抑制模型如图2所示。该模型包括发送节点、协作干扰节点和接收节点，每个节点都配备单天线。发送节点和协作干扰节点的比特流通过调制、数模转换和射频处理后经天线发射，接收节点收到期望信号和干扰信号的叠加信号，经过下变频、模数转换和干扰抑制后，解调得到期望信号的估计值。

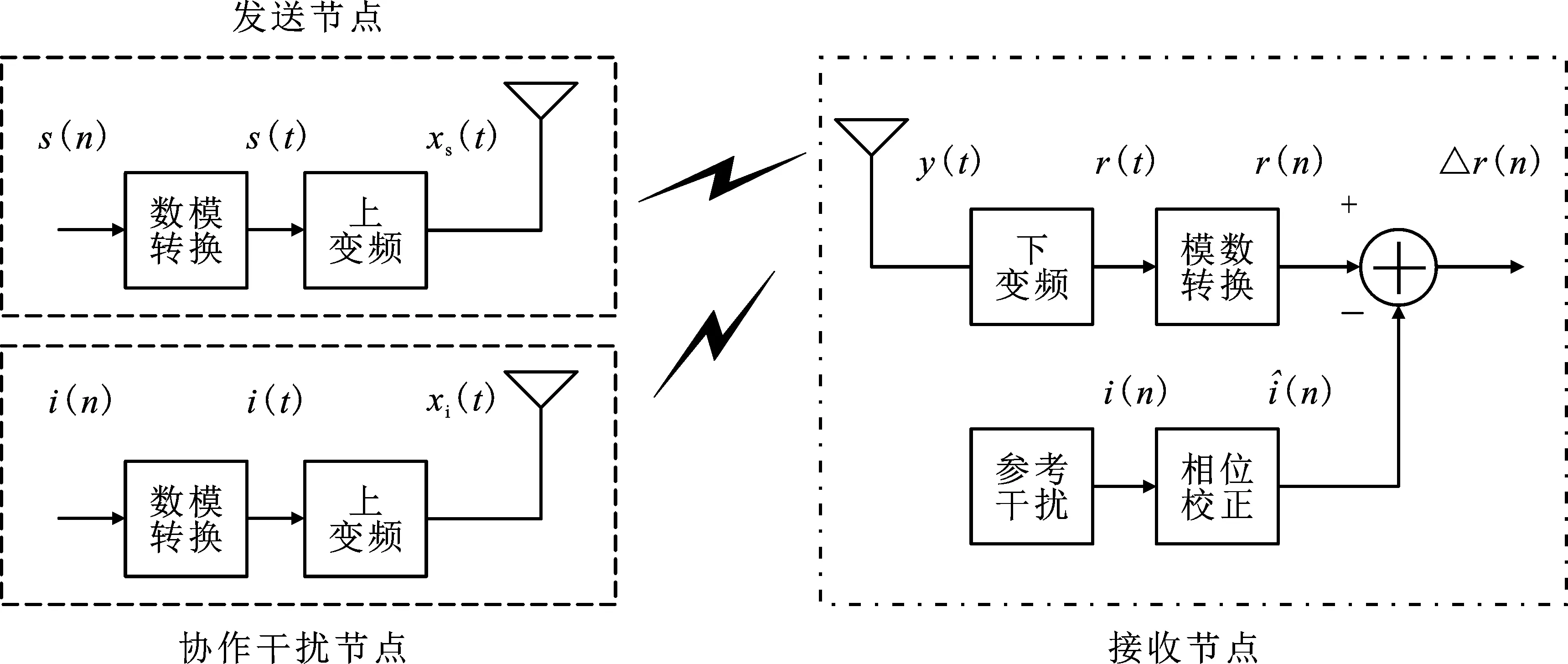
图2 协作干扰抑制示意图

1.1 发送节点模型

首先考虑发送节点。假设发送节点的基带离散信号为s(n)∈{0，1}，经过数模转换后，变为基带连续信号，记作s(t)。s(t)经过上变频后由射频天线发射出去，发射信号可以表示为

xs(t)=(Ps)1/2s(t)exp(j(2πfst+φs)) ，

(1)

其中，Ps是发送节点发射信号的功率，fs是通信信号的载波频率，φs为通信信号载波的初始相位。

1.2 协作干扰节点模型

类似地，定义协作干扰节点的基带离散信号为i(n)，经过数模转换后，变为基带连续信号i(t)。i(t)上变频后通过射频天线发射出去，发射信号可以表示为

xi(t)=(Pi)1/2i(t)exp(j(2πfit+φi)) ，

(2)

其中，Pi是协作干扰节点发射信号的功率，fi是协作干扰信号的载波频率，φi为协作干扰信号载波的初始相位。

1.3 信道模型

假设通信信号和协作干扰信号都经历加性高斯白噪声(Additive White Gaussian Noise，AWGN)信道，经过无线信道传输，接收节点接收到的射频信号为[12]

y(t)=Asxs(t-ts)+Aixi(t-ti)+n(t) ，

(3)

其中，As和Ai分别是通信信号和协作干扰信号经历的信道衰减因子，不失一般性，假设为1[13]；ts为通信信号的传输时延；ti为干扰信号的传输时延；n(t)是均值为零、方差为σ2的加性高斯白噪声。

1.4 接收机模型

经过下变频后，基带接收信号为

r(t)=y(t)exp(-j(2πfr+φr))=(Ps)1/2s(t-ts)exp(j(2πΔfst+Δφs))+

(Pi)1/2i(t-ti)exp(j(2πΔfit+Δφi))+w(t) ，

(4)

其中，fr是接收节点的载波频率；φr为载波的初始相位；Δfs=fs-fr和Δφs=φs-φr分别是通信信号收发端的载波频率偏移和初始相位误差；Δfi=fi-fr和Δφi=φi-φr分别是协作干扰信号收发端的载波频率偏移和初始相位误差；w(t)=n(t)exp(-j(2πfr+φr))，是等效基带噪声。

式(4)第1项记作rs(t)，为通信信号分量；第2项记作ri(t)，为干扰信号分量，则接收信号重新表达为

r(t)=rs(t)+ri(t)+w(t) 。

(5)

以1/Ts的采样率进行采样，对接收信号做模数转换，得到基带接收信号的离散形式：

r(n)=(Pi)1/2i(n-τ1)exp(j(2πεn+Δφi))+rs(n)+w(n) ，

(6)

其中，τ1=ti/Ts，为干扰信号归一化时延；ε=ΔfiTs，为归一化频率同步误差。式(6)第1项记作ri(n)，为干扰信号的离散形式；第2项和最后一项分别是离散化的通信信号和噪声。

(7)

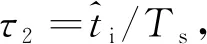
干扰抑制后的信号为

(8)

干扰抑制后的残余干扰分量为

(9)

以下将研究归一化时间同步误差τ=|τ1-τ2|和归一化频率同步误差ε对干扰抑制性能的影响。为了分析方便，假设通信信号和协作干扰信号相互独立，且通信信号和协作干扰的载波初始相位均为0，即Δφs=Δφi=0。

2 性能指标分析

2.1 残余干扰功率

式(9)得到了时频同步误差对残余协作干扰信号影响的闭合表达式。下面将计算残余干扰功率。不失一般性，设协作干扰信号为伪随机序列[14]，则残余干扰功率为

PΔ=E{Δ(n)Δ*(n)} ，

(10)

其中，(·)*表示取共轭。

将式(9)代入式(10)，得到

(11)

三角函数的求和公式[15]如下所示：

(12)

将式(12)代入式(11)，得到残余干扰功率的闭合表达式为

(13)

其中，R(τ)是伪随机序列的自相关函数。在接收机进行信号时间同步时，常见的时间同步算法可以将时间同步误差控制在1个符号周期以内。因此，不考虑整数倍的同步时延误差，重点研究小数时延的影响[16]：

i(n-τ)=τi(n-1)+(1-τ)i(n) 。

(14)

进行功率归一化处理后，得

(15)

(16)

将式(16)代入式(13)，得

(17)

下面分别讨论归一化时延和频偏对残余干扰功率的影响。为了与后续仿真条件对应，取伪随机序列长度N=1 023。

(1) 当归一化频偏为0时，式(17)退化为

(18)

特别地，当τ=0时，时频完全同步，残余干扰功率为0；当τ=0.63时，残余干扰与抑制前干扰功率相同；当τ=1时，接收的干扰信号与重建干扰信号不相关，功率加倍。

(19)

(2) 当归一化时延为0时，式(17)退化为

(20)

特别地，当ε=0时，时频完全同步，残余干扰功率为0；当ε=3×10-4时，残余干扰与抑制前干扰功率相同；当ε=10-2时，接收的干扰信号与重建干扰信号不相关，功率加倍。

(21)

2.2 干扰抑制比

定义干扰抑制比(Jamming Cancellation Ratio，JCR)来度量无线通信系统对协作干扰信号的抑制程度[17]，用干扰抑制前后干扰加噪声功率之比表示。干扰抑制比越大，系统对干扰信号的抑制效果越好。

(22)

从式(22)可以看出，干扰抑制比是关于残余干扰功率的减函数。根据节2.1的结论可知：当τ=0，ε=0时，PΔ=0，干扰抑制比达到最大值：

(23)

其中，RJNR是干噪比；RJSR是干信比；RSNR是信噪比。

当τ和ε继续增加时，干扰抑制比逐渐降低。特别地：当ε=0、τ=0.63或者τ=0、ε=3×10-4时，PΔ=Pi，干扰抑制比为0；当ε=0、τ=1或者τ=0、ε=10-2时，PΔ=2Pi，干扰抑制比为-3 dB。

2.3 解调误码率

考虑通信信号调制方式为正交相移键控(Quadrature Phase Shift Keying，QPSK)。接收端干扰抑制完成后，需要进行QPSK解调恢复原始比特流，解调误码率与解调器输入信噪比γ有关。解调时，残余干扰作为噪声处理。QPSK解调器的输入信噪比为

(24)

其中，Ps是通信信号功率，PΔ是干扰抑制后的残余干扰功率。

高斯信道下QPSK的解调误码率为[18]

pQPSK=Q(γ1/2) 。

(25)

将式(24)代入式(25)，得到协作干扰信号存在时频同步误差时，授权用户解调误码率为

(26)

2.4 保密容量

保密容量定义为最大可达保密速率。在加性高斯白噪声窃听信道中，保密容量定义如下[19]：

(27)

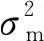
协作干扰抑制后，安全通信保密容量为

(28)

从式(28)可以看出，保密容量是关于残余干扰功率的减函数。根据节2.1的结论可知：当τ=0，ε=0时，保密容量达到最大值，即

(29)

随着τ和ε取值增大，保密容量逐渐降低。特别地，当ε=0、τ≥0.63或者τ=0、ε≥3×10-4时，保密容量为0，此时无法实现安全通信。

3 数值与仿真结果

为验证协作干扰时频同步误差对干扰抑制比、解调误码率和保密容量这3个性能指标的影响，通过MATLAB仿真软件，分别在不同信噪比和不同时频同步误差下进行实验，仿真实验参数如表1所示。取10 000帧数据统计平均后作为实验结果。为方便对比，在表1所示仿真参数设置下，信噪比为10 dB时，由式(29)可得无时频同步误差时的系统保密容量最大值Cmax=1.662 bit/(s·Hz)。

表1 仿真参数设置

3.1 时延误差对干扰抑制比、误码率和保密容量的影响

图3～图5给出在归一化频偏为0，不同信噪比下，归一化时延与干扰抑制比、误码率和保密容量之间的关系。仿真结果显示，随着时延增大，系统对协作干扰信号的抑制程度降低，干扰抑制比降低，保密容量降低，误码率增加。

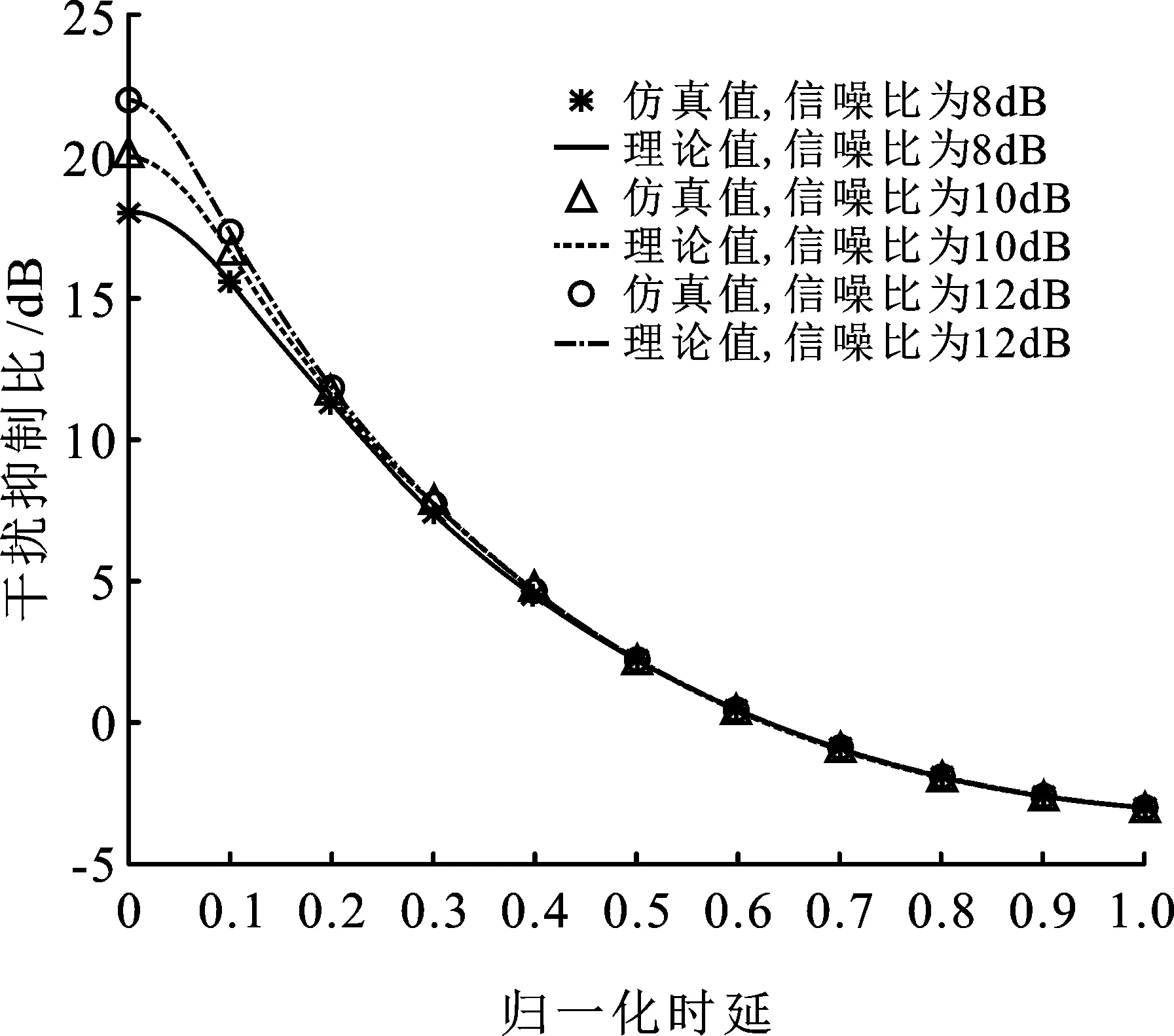
图3 归一化频偏为0时，不同信噪比下归一化时延与干扰抑制比关系示意图

图3显示了时延对干抑制比的影响。以信噪比10 dB曲线为例，干扰抑制比随着时延增大而降低。当归一化时延为0.1时，干扰抑制比下降3.5 dB，约17.5%；当归一化时延大于0.63时，干扰抑制比小于0 dB。这是因为接收信号的干扰分量与接收机重建的干扰信号叠加，使干扰信号功率增大。当归一化时延为1时，干扰抑制比为-3 dB，接收干扰信号分量和重建干扰信号互不相关，因此功率加倍，系统的干扰抑制能力最差。

图4显示了时延对QPSK解调误码率的影响。随着时延增大，误码率增加。当归一化时延大于0.63时，不同信噪比的误码率曲线重合并趋于最大误码率，此时时延成为误码率的主要影响因素。

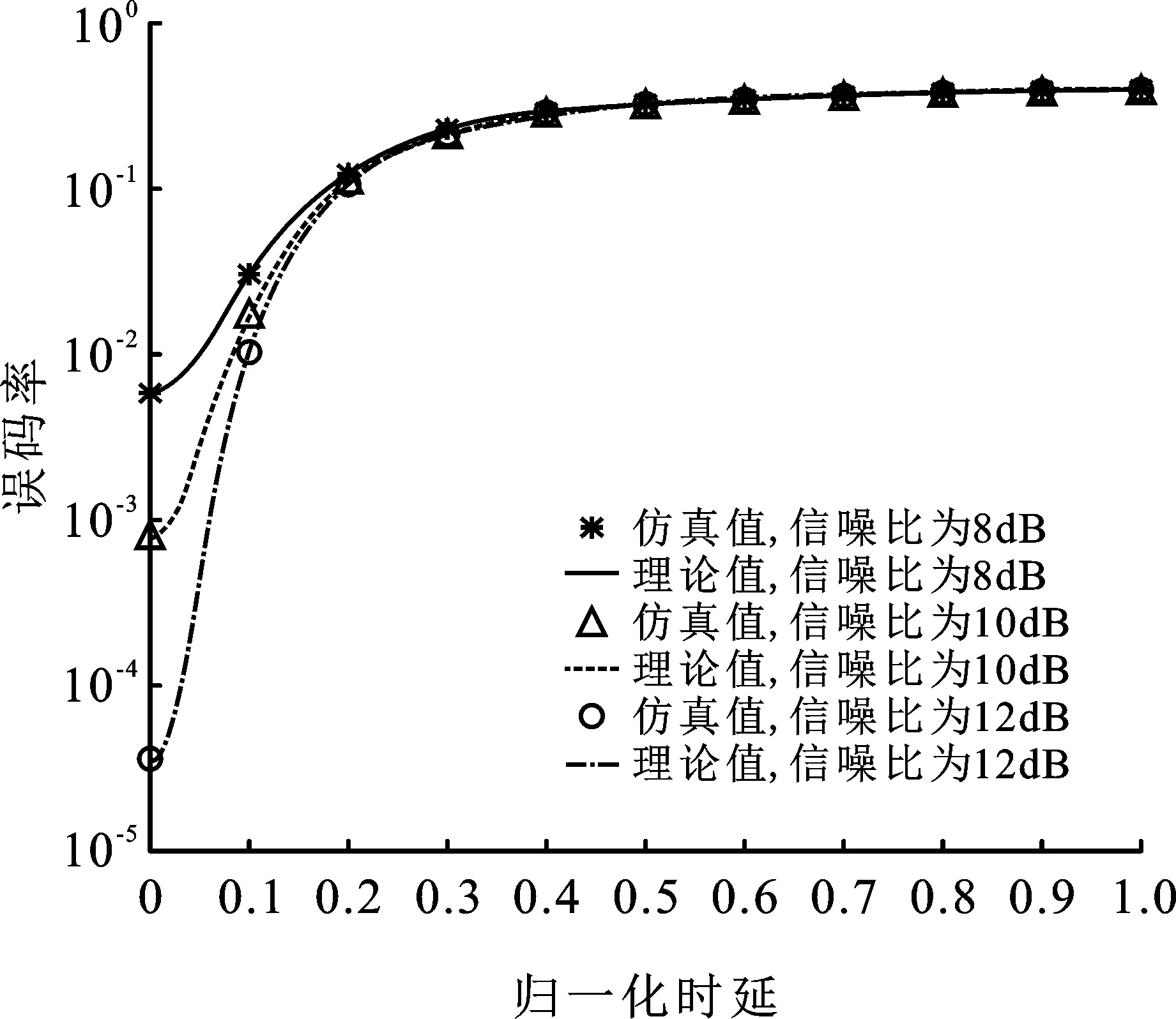
图4 归一化频偏为0时，不同信噪比下归一化时延与误码率关系示意图

图5显示了时延对保密容量的影响。随着时延增大，保密容量降低。以信噪比10 dB曲线为例，当归一化时延为0.1时，保密容量下降0.5 bit/(s·Hz)，约30%；当归一化时延大于0.63时，保密容量为0，主信道条件差于窃听信道条件，此时无法实现安全通信。

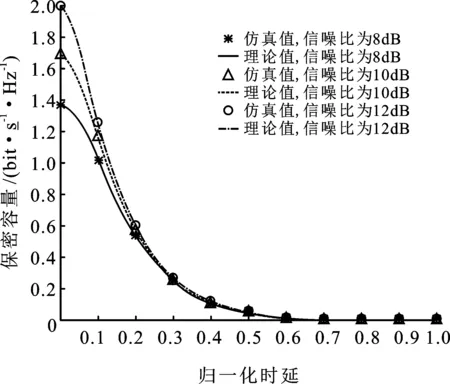
图5 归一化频偏为0时，不同信噪比下归一化时延与保密容量关系示意图

3.2 频偏对干扰抑制比、误码率和保密容量的影响

图6～图8显示了频偏对干抑制比、误码率和保密容量的影响。

图6中，以信噪比10dB曲线为例，归一化频偏为10-5时，干扰抑制比下降0.6 dB，约3%；当归一化频偏大于3×10-4时，干扰抑制比小于0，接收信号干扰分量与重建干扰叠加使干扰信号功率增大；在归一化频偏达到10-2时，接收干扰分量和重建干扰信号互不相关，功率加倍，干扰抑制比为-3 dB。

图6 归一化时延为0时，不同信噪比下归一化频偏与干扰抑制比关系示意图

图7给出归一化时延为0时，不同信噪比下归一化频偏与QPSK解调误码率之间的关系。随着频偏增大，误码率提高。当归一化频偏大于3×10-4时，不同信噪比的误码率曲线重合并趋于最大误码率，此时频偏成为误码率的主要影响因素。

图7 归一化时延为0时，不同信噪比下归一化频偏与误码率关系示意图

图8给出归一化时延为0时，不同信噪比下归一化频偏与保密容量之间的关系。随着频偏增大，保密容量降低，以信噪比10 dB曲线为例，归一化频偏为10-5时，保密容量下降0.1 bit/(s·Hz)，约6%；当归一化频偏大于3×10-4时，保密容量为0，主信道条件差于窃听信道条件，此时无法实现安全通信。

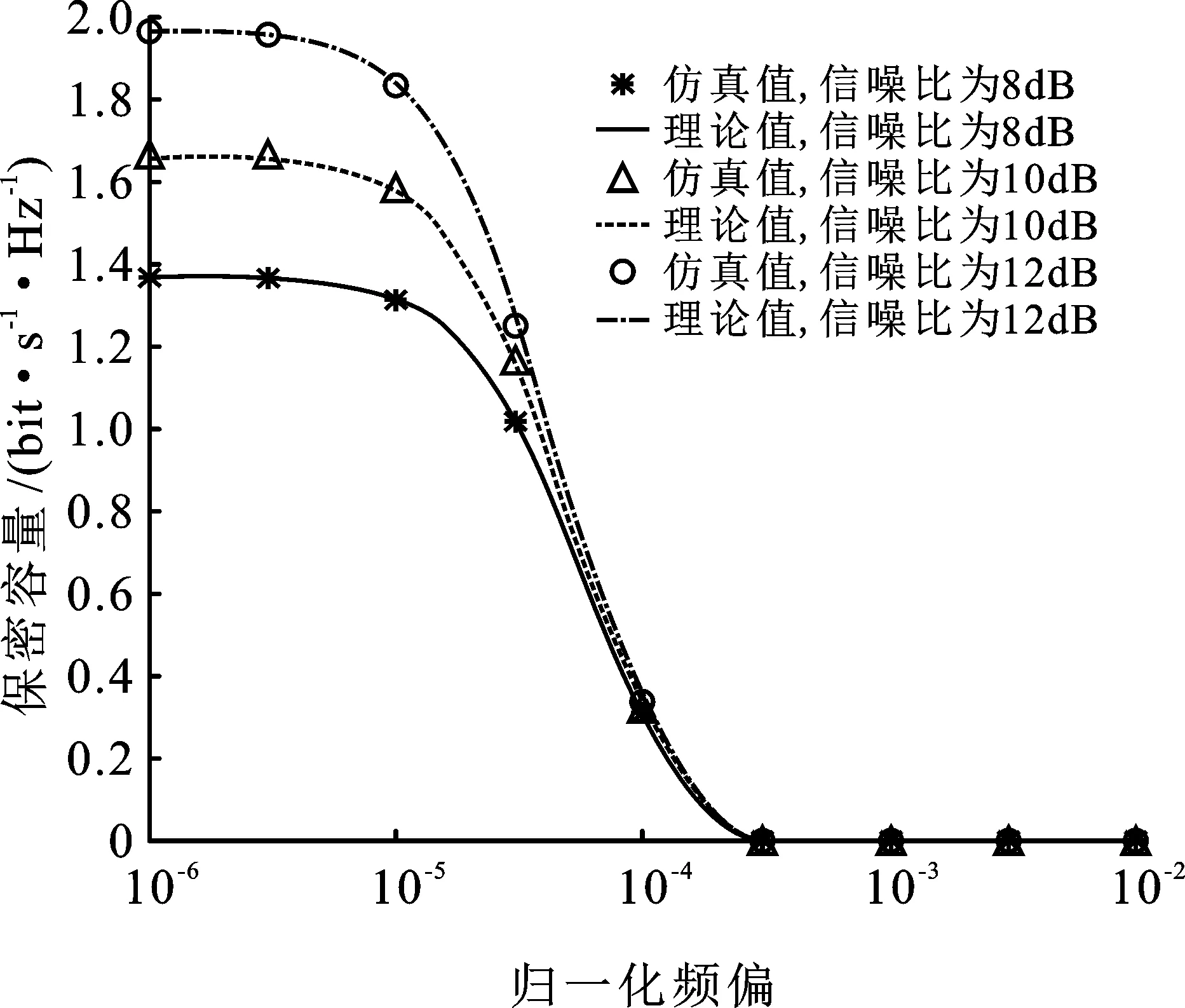
图8 归一化时延为0时，不同信噪比下归一化频偏与保密容量关系示意图

3.3 时频同步误差对干扰抑制比、误码率和保密容量的影响

图9～图11显示了信噪比为10 dB下，存在时频同步误差对系统协作干扰信号的抑制性能影响的等高线。随着时延或频偏增大，系统对协作干扰信号的抑制程度降低，干扰抑制比和保密容量降低，误码率增加。

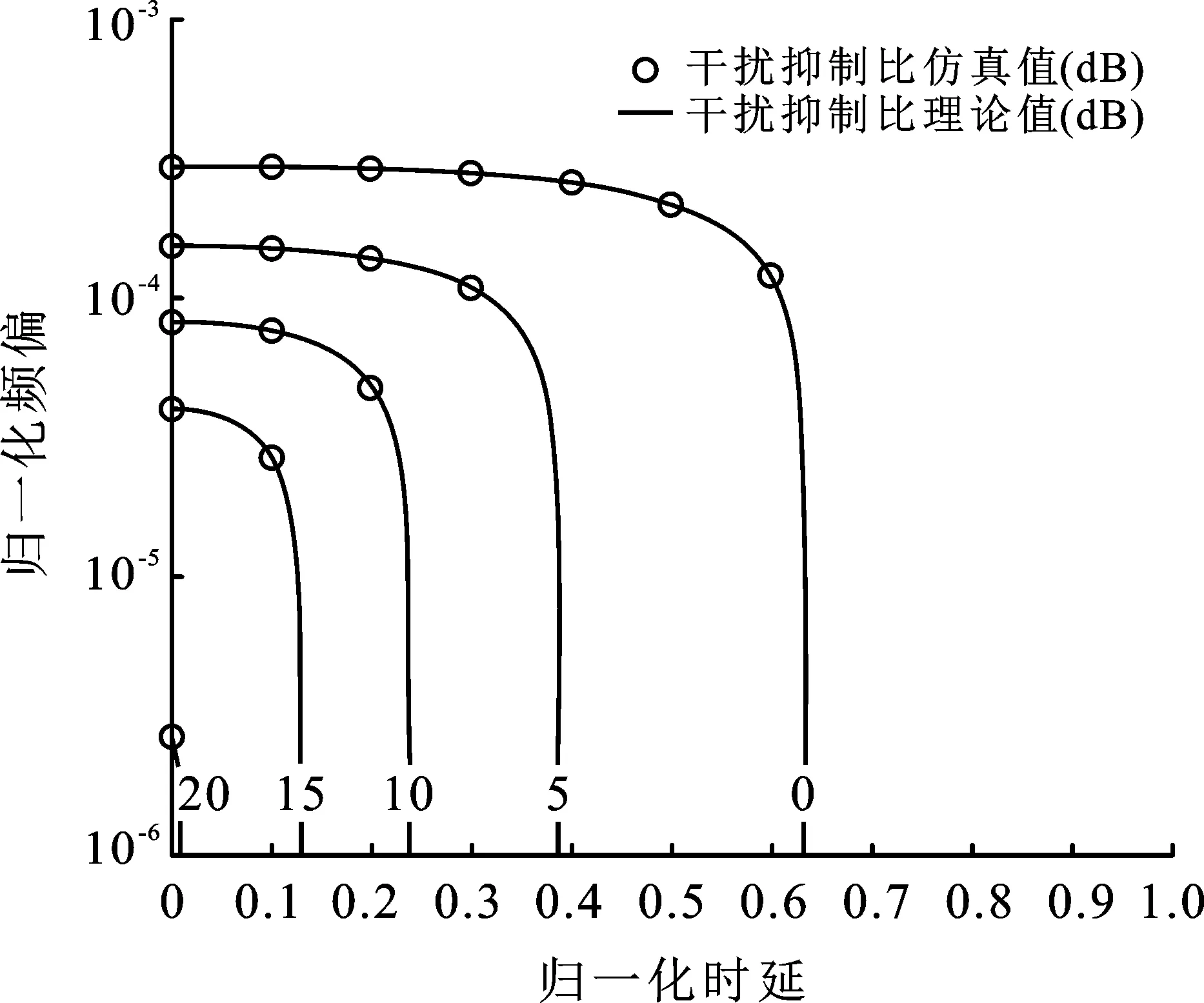
图9 信噪比为10 dB，且存在时频同步误差时，干扰抑制比等高线示意图

图9给出了干扰抑制比等高线示意图，当时频同步误差增大时，系统的干扰抑制比降低。当归一化时延为0.24，频偏小于10-4时，干扰抑制比保持为10 dB。

图10显示了解调误码率的等高线变化情况，随着时延或频偏增大，误码率升高。当归一化时延为0.26，频偏小于10-4时，误码率保持为0.2。

图10 信噪比为10 dB且存在时频同步 误差时，误码率等高线示意图

图11给出了存在时频同步误差时，保密容量的等高线。当时频同步误差增大时，系统保密容量降低。当归一化时延小于0.06且频偏小于10-5时，保密容量损失小于16%；当归一化时延为0.25且频偏小于10-4时，保密容量保持为0.4 bit/(s·Hz)。为了使得保密容量大于0，应该满足约束条件，即归一化时延小于0.63且频偏小于3×10-4。

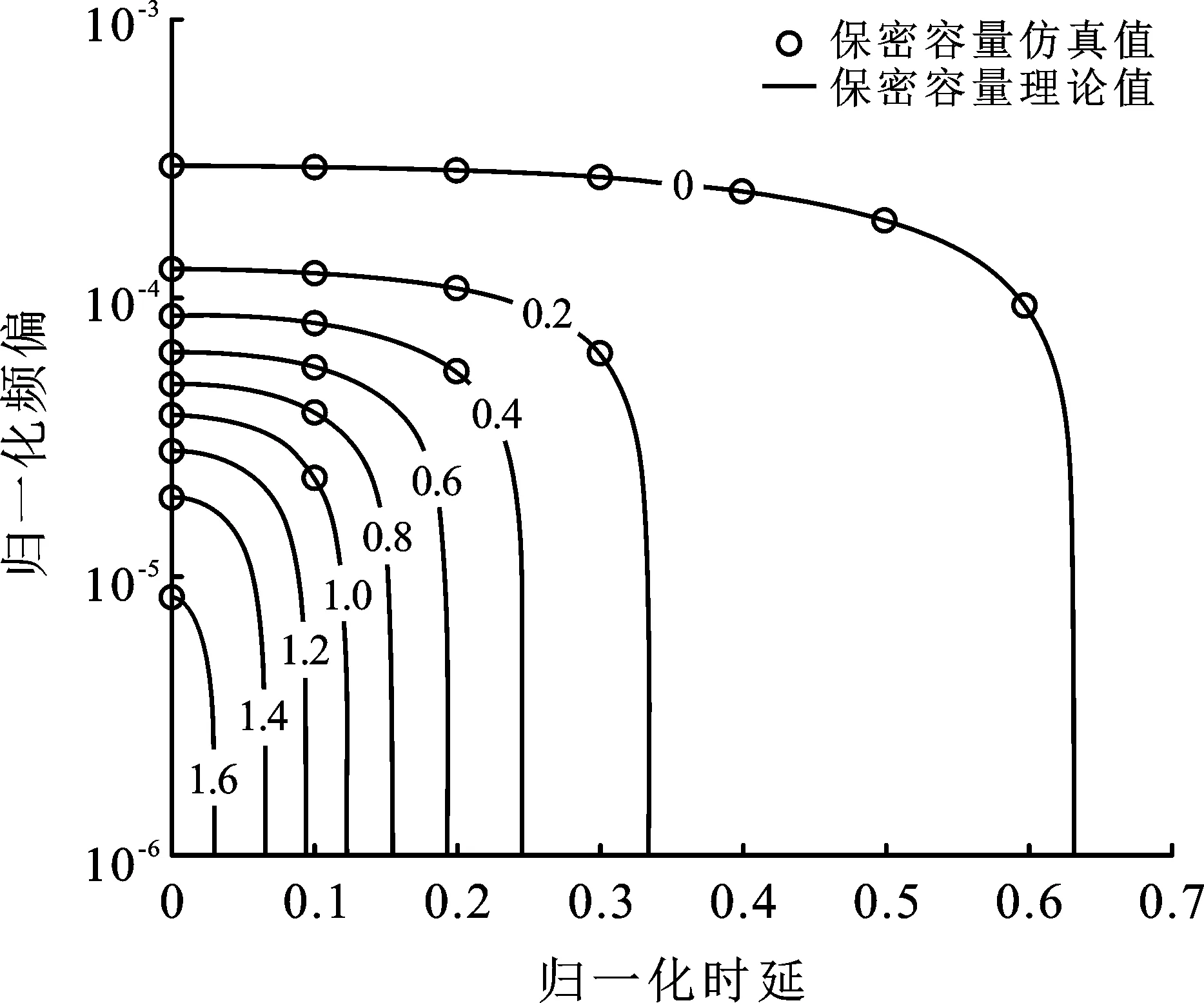
图11 信噪比为10 dB且存在时频同步 误差时，保密容量等高线示意图

4 结束语

笔者研究了高斯窃听信道下，协作干扰时频同步误差对干扰抑制比、误码率和保密容量的影响，并根据残余干扰信号功率推导出安全通信保密容量的闭合表达式。理论和仿真结果显示，当归一化时延小于0.06且频偏小于10-5时，保密容量损失小于16%。当归一化时延小于0.63且频偏小于3×10-4时，保密容量大于0，可以实现安全通信。研究成果可为安全通信系统的设计提供理论支持和工程参考。