新型深度矩阵分解及其在推荐系统中的应用
史加荣,李金红
(西安建筑科技大学 理学院,陕西 西安 710055)
近年来,计算机系统结构(例如硬盘、CPU)的快速发展,使网络数据呈现爆炸式增长,用户难以从众多信息中找到感兴趣的内容。为快速检索和提供用户所需信息,帮助用户过滤无效的内容,HANANI等提出了信息过滤技术[1],故而产生了推荐系统(Recommendation System,RS)[2]。推荐系统主要解决信息过载问题,即从亿万信息中提取针对不同用户感兴趣的项目和商品等,并推荐给用户。对于商家,运用推荐系统能够将自己的产品高效快速地推荐到用户面前,并被用户了解和知晓,带来实际可观的收益。当前,网络APP大都包含推荐系统,例如:购物软件(淘宝、京东)、视频软件(腾讯、爱奇艺、优酷)、音乐软件(网易云音乐、QQ音乐)和搜索引擎(谷歌、百度)等都包括“猜你喜欢”“为你推荐”等板块。个性化推荐系统已成为互联网产品的标配[3],也是人工智能领域得以实现的基础[4]。
由于机器学习可以挖掘海量数据所蕴含的规律,因此,研究者将机器学习算法融入到推荐系统,初步取得了良好的效果[5-6]。但随着大数据时代的到来,推荐系统中数据的稀疏性[7]、冷启动[8]和可解释性[9]等问题越来越严重,且有的推荐系统根据用户的一次搜索和查阅便大规模地推荐类似信息,导致用户的不良体验。故而,当前推荐算法的用户满意度低,越来越多的用户希望拥有更智能化的推荐,以符合他们的需求[10]。为此,不断有学者致力于研究和改进各种推荐算法,希望能够缓解推荐系统所面临的问题,提高用户满意度。
1 相关工作
作为当前推荐系统的主流算法,协同过滤(Collaborative Filtering,CF)[11]主要分为基于内存、模型和深度学习3类[12],其中第2类主要包含矩阵分解模型。下面介绍与文中相关的矩阵分解和深度矩阵分解方法。
1.1 矩阵分解
在2006年的Netflix大赛中,基于模型的矩阵分解以优良的推荐性能赢得了大赛第一名[13]。之后,该类方法受到了学术界的广泛欢迎。文献[14]总结并提出了最常见的几种矩阵分解的推荐方法,包括基本矩阵分解(MF)、加入偏置的奇异值分解(Bias-SVD)、引入时间因子的奇异值分解(SVD++)。这里,用m×n维矩阵R=(rij)m×n表示m个用户对n个项目的评分矩阵,基本矩阵分解形式为
R≈PQT,
(1)
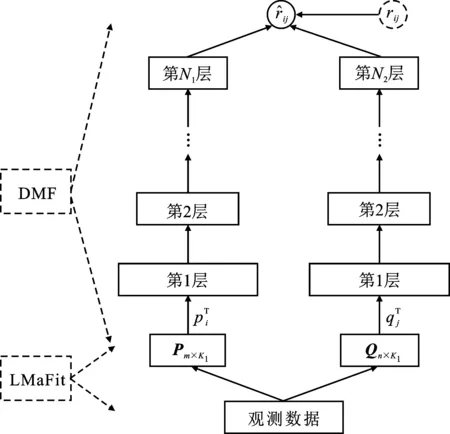
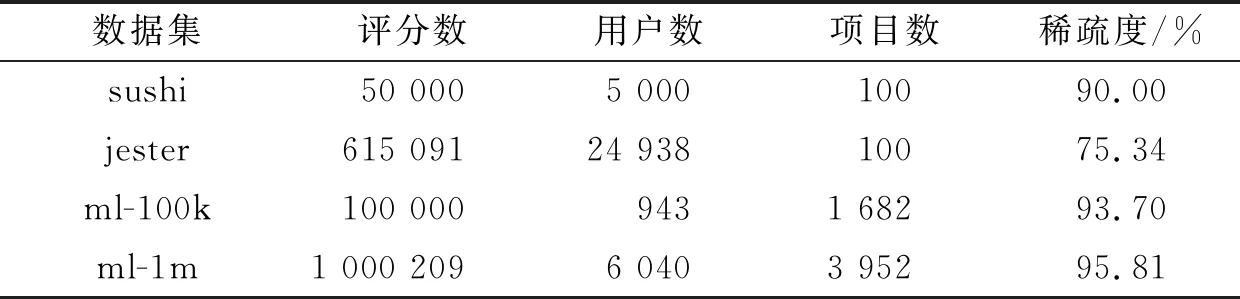
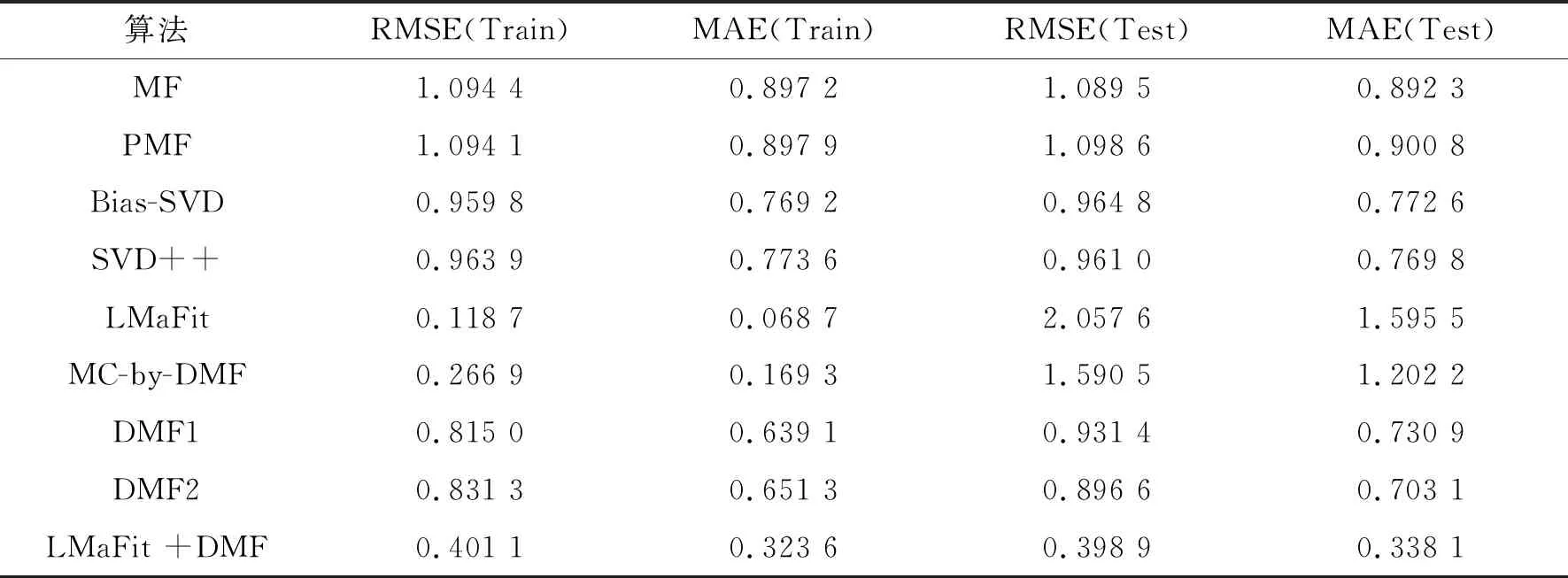
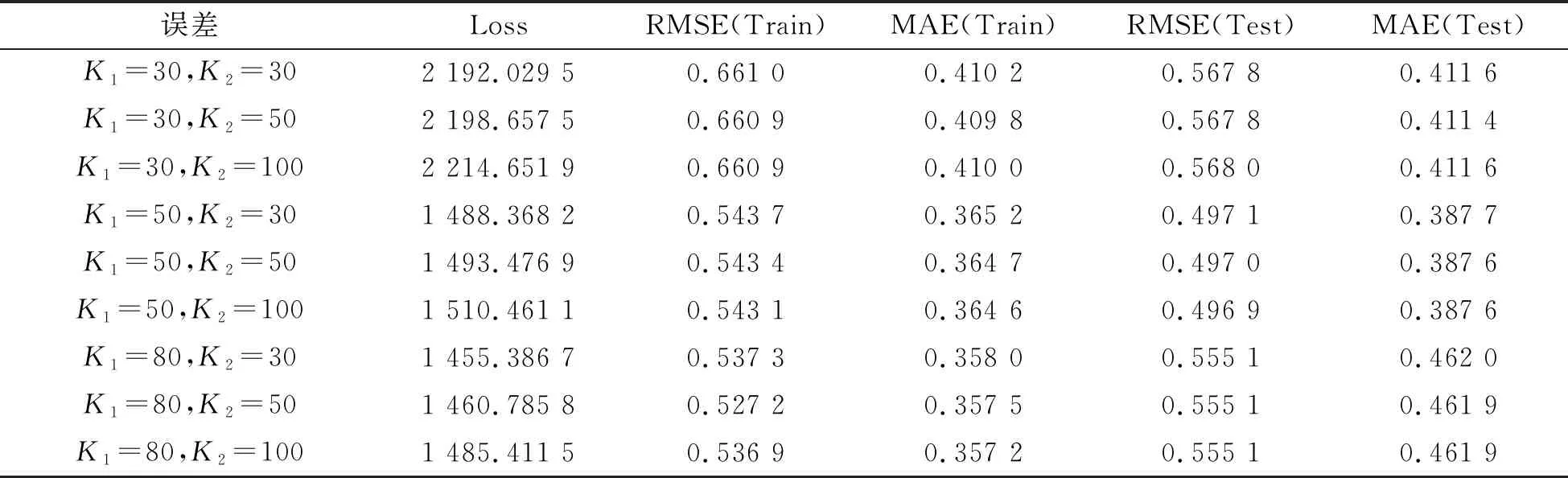
其中,P∈Rm×K1为用户隐特征矩阵,Q∈Rn×K1为项目隐特征矩阵,K1 对于评分值rij,其预测公式为 (2) 其中,pi∈R1×K1表示P的第i行对应的向量;qj∈R1×K1表示Q的第j行对应的向量。 为了得到最优的隐特征矩阵,建立如下的正则化损失函数: (3) 其中,Ω⊂{1,2,…,m}×{1,2,…,n}表示所有已知评分指标集合,η>0为正则化系数,‖·‖是向量的L2范数。 由于随机梯度下降法(Stochastic Gradient Descent,SGD)易于实现且运行时间较快[15],因此可采用SGD来最小化式(3)。该方法循环遍历训练集中的所有评分。对于给定的隐特征向量对(pi,qj),系统都会预测其评分值,并将预测误差定义为 (4) 对损失函数求一阶梯度,在梯度的反方向上按与学习率λ成正比来更新变量: (5) 传统矩阵分解在面对高维稀疏且规模较大的数据时,存在很大的缺陷,且对非线性结构的数据无效,最终,导致推荐精度不高。近年来,深度学习在图像处理等领域取得了突破性的进展[16-17],并通过实验分析验证其更适用于大型数据。因此,一些学者便将神经网络技术融入推荐系统,利用非线性映射打破传统矩阵分解对非线性数据无效的瓶颈,提出深度矩阵分解(Deep Matrix Factorization,DMF)。文献[18]利用广义矩阵分解的线性核来对潜在特征交互进行建模,根据多层感知器的非线性核学习交互功能,通过共享相同的嵌入层进行融合,提出了神经协同过滤技术。该方法将数据矩阵中已知元素用“1”代替,未知评分用“0”代替,即 (6) 将矩阵的第i行Xi·,第j列X·j同时输入到多层神经网络,得到一种深度矩阵分解模型[18]。文中将此模型记为DMF1。文献[19]在DMF1的基础上,充分利用原始评分信息反映已知评分值,用“0”代替矩阵中的未知元素,即 (7) 该模型将Xi·和X·j作为多层神经网络的输入,其记为DMF2。文献[20]利用数据中的隐式信息,开发了隐式反馈嵌入,将高维稀疏的隐式信息转换为保留主要特征的低维向量,提高了训练效率。文献[21]利用深度矩阵分解进行矩阵补全(Matrix Completion,MC),同时优化了多层神经网络的输入和参数,将隐特征变量传递到输出层来恢复缺失值,并记为MC-by-DMF。 基本矩阵分解采用双线性映射,导致推荐性能较差,而且不适用于大规模且具有非线性结构的数据。现有的深度矩阵分解虽然利用非线性映射,但其输入向量稀疏、维数高或求解复杂,从而影响推荐性能。为克服现有深度矩阵分解的缺陷,提出一种新型深度矩阵分解模型,并设计了一种求解算法(LMaFit+DMF):先使用低秩矩阵拟合(Low-rank Matrix Fitting,LMaFit)确定神经网络的输入隐特征,再通过深度神经网络求解模型参数。 对于已知元素rij,若直接对两个隐特征向量pi和qj采用内积运算,则无法突破rij与pi、qj之间的双线性关系。为此,分别对隐特征向量pi和qj建立两个多层感知器。对用户隐特征向量pi,采用含有N1个隐层的多层感知器建立非线性映射: (8) 类似地,对项目隐特征向量qj,构建含有N2个隐层的多层感知器: (9) 为了预测评分rij,进一步要求UN1=VN2=K2。引入K2维列向量h,建立如下预测模型: (10) (11) (12) 在上述模型中,两个多层感知器的输入均为变量,故同时关于变量θ1和θ2来最小化目标函数是比较复杂的。 采用两阶段法来简化新型深度矩阵分解模型的求解,即先确定θ1,再求解θ2。 (13) (14) 其中,Λ∈Rm×n为拉格朗日乘子矩阵,〈·,·〉表示两矩阵的内积。对该函数的各个矩阵变量求梯度,得一阶最优条件: (15) 其中,ΩC为集合Ω的补集。通过非线性的连续超松弛算法求解方程组(15),得到迭代公式: (16) 其中,权重参数ω≥1。 一旦θ1确定,所建立的深度矩阵分解模型就变成了传统的多层神经网络。求解深度神经网络最常用的优化方式是随机梯度下降法,它包括多种具体实现方式[15]。在第二阶段,将通过比较不同优化器,采取最适合的优化器求解如下多层神经网络: (17) (18) 其中,λ为学习率,λ>0。 1.3 麻醉方法 腰硬联合麻醉8例,其中3例第1次腰穿失败后立即改全身麻醉,其余121例患者均为全身麻醉。 依据最终得到的深度矩阵分解,联合使用用户嵌入特征f1(pi)和项目嵌入特征f2(qj)对未知评分rij进行预测,参见式(10)。图1展示了低秩矩阵拟合与深度矩阵分解的联合框架。 图1 低秩矩阵拟合和深度矩阵分解的联合框架 为验证LMaFit+DMF的可行性和有效性,选取4个公开的数据集:sushi[24]、jester(http://eigentaste.berkeley.edu/dataset/)、ml-100k和ml-1m(https://grouplens.org/datasets/movielens/)进行实验。Sushi根据用户的口味和喜好等对寿司给出-1至4之间的整数评分;jester反映了用户对不同类笑话的偏好程度,将评分值控制在-10到10之间;ml-100k和ml-1m均为公开电影评分数据集,其值在1到5之间。表1总结了这4个数据集的基本信息。 表1 数据集的基本信息 实验在Windows 10 64位操作系统、Core i5-6300HQ处理器和12 GB内存下运行。LMaFit和MC-by-DMF均由Matlab编程实现,其他方法使用Python语言。对于所有深度矩阵分解方法,设置迭代次数为 1 000,批大小为12 500,正则化参数置为0.5,学习率为0.000 1。对于LMaFit+DMF,令N1=N2=N。在传统矩阵分解、LMaFit和MC-by-DMF中,将数据集按7∶3随机划分为训练集和测试集;在其他方法中,将数据集按7∶1∶2随机划分为训练集、验证集和测试集。采用均方根误差(RMSE)和平均绝对误差(MAE)作为推荐效果的评价指标: (19) (20) 其中,|Ω|为已知的用户-项目交互数目。它们的值越小,推荐系统的准确度就越高。 首先以数据集ml-100k为例,将所提出的LMaFit +DMF与传统的矩阵分解(MF、PMF、Bias-SVD、SVD++、LMaFit)和现有的深度矩阵分解(MC-by-DMF、DMF1、DMF2)进行比较,其中PMF(ProbabilisticMatrix Factorization)采用极大后验估计推测用户与项目特征。设置迭代次数均为1 000,学习率和正则化参数分别为0.000 1和0.5。在传统的矩阵分解和LMaFit +DMF中,设置隐向量的维数K1均为100。对于MC-by-DMF,按照文献[21]设置含有两个隐层的网络,节点数目分别为10、100,激活函数分别为Tanh和Linear。在DMF1、DMF2和LMaFit +DMF中,设置神经网络隐层层数均为1,使用Relu激活函数,优化器为Adam,且隐特征向量的输出维数K2为 50。前述9种推荐算法在训练集和测试集上的误差比较如表2所示。 表2 不同推荐方法在ml-100k上的性能比较 从表2可以看出:虽然LMaFit和MC-by-DMF在训练集的评价指标上取得了较小的误差,但其在测试集上却非常大,这意味着LMaFit和MC-by-DMF具有较差的泛化性能。与MF、PMF、Bias-SVD和SVD++相比,DMF1和DMF2的训练集RMSE至少下降了0.144 8,MAE至少下降了0.130 1;测试集RMSE至少下降了0.064 4,MAE至少下降了0.066 7,故这两种深度矩阵分解优于传统的矩阵分解。与DMF1和DMF2相比,LMaFit +DMF训练集的RMSE至少下降了0.413 9,MAE至少下降了0.315 5;测试集的RMSE至少下降了0.497 7,MAE至少下降了0.365 0。因此,在上述9种推荐算法中,LMaFit +DMF取得了最佳的推荐性能,且改善结果显著。 其次,在sushi、jester和ml-1m数据集上比较不同深度矩阵分解方法的性能。由于MC-by-DMF不适用于较大规模的数据集,故在jester和ml-1m的实验中未考虑该方法。在LMaFit+DMF中,设置K1分别为80、80、500,K2分别为 50、100、50。对于sushi,MC-by-DMF的节点数目分别为10、100。实验结果见表3至表5。 表5 不同深度矩阵分解方法在ml-1m上的性能比较 从表3可以得出如下结果:MC-by-DMF的训练误差非常小,测试误差非常大;与DMF1和DMF2相比, LMaFit+DMF在训练集上RMSE下降范围在0.110 3~0.572 9,MAE的范围在0.139 8~0.538 4;在测试集上的RMSE下降范围在0.656 2~1.909 2,MAE的范围在0.514 7~1.628 9。 表3 不同深度矩阵分解方法在sushi上的性能比较 从表4可以看出:与DMF1相比,数据集jester的LMaFit+DMF在训练集上的评价指标至少下降了0.427 3,在测试集上的评价指标至少下降了0.517 6;虽然DMF2训练集的各评价指标都非常低,但测试集评价指标却非常大,因此该模型对于jester的推荐性能较差。 表4 不同深度矩阵分解方法在jester上的性能比较 比较表5得出如下结论:与DMF1和DMF2相比,数据集ml-1m的LMaFit+DMF在训练集上RMSE下降范围在0.219 4~0.225 3,MAE的范围在0.229 1~0.232 6;在测试集上的RMSE下降范围在0.313 2~0.319 5,MAE的范围在0.286 5~0.321 1。因此,在sushi、jester和ml-1m数据集上,LMaFit+DMF明显优于其他的深度矩阵分解算法。 在LMaFit+DMF中,将LMaFit方法得到的隐特征向量作为多层神经网络的输入,显著地降低了输入特征的维数。最后在sushi、jester、ml-100k和ml-1m这4个数据集下,比较DMF1、DMF2和LMaFit+DMF运行时间。对于数据集sushi、jester、ml-100k和ml-1m,DMF1每次迭代(epoch)的平均运行时间分别为1.607 9 s、56.512 0 s、1.893 5 s和35.263 4 s,DMF2的平均运行时间分别为1.614 6 s、56.878 1 s、1.922 1 s和38.511 9 s,而LMaFit+DMF下的平均运行时间分别为0.039 1 s、0.388 6 s、0.020 0 s和0.059 6 s。由于DMF1和DMF2的网络输入特征维数接近,故它们的运行时间非常接近。由于较低的隐特征维数,LMaFit+DMF的运行时间短,每次迭代的时间至少降低了97.5%。综上,笔者提出的深度矩阵分解算法不仅显著地改善了推荐性能,而且降低了算法的运行时间。 为了选择最适合笔者所提方法的梯度更新策略,对4种常用的优化器Adadelta、Adagrad、Adam和RMSProp进行对比[15]。在sushi、jester、ml-100k和ml-1m数据集上进行实验,K1分别设置为80、80、100、500,K2分别设置为50、100、50、50,激活函数均取为Relu,神经网络的层数均为1。实验结果如表6至表9所示。 表6 数据集sushi下不同优化器的实验结果 表7 数据集jester下不同优化器的实验结果 表8 数据集ml-100k下不同优化器的实验结果 表9 数据集ml-1m下不同优化器的实验结果 从表6至表9可以看出:优化器RMSProp的损失函数值均达到最小;对于训练集, Adam的RMSE和MAE均取得最小值;在测试集中,Adam和RMSProp的误差较小。因此,在后面的实验中选取性能较优的Adam作为优化器。 9 ml-1m在不同隐层下训练集的RMSE 先考虑用户或项目对应的多层感知器的输入特征维数K1和输出特征维数K2对LMaFit+DMF的影响。根据4个数据集的维数大小来设置K1,在sushi和jester中取K1∈{30,50,80};在ml-100k中取K1∈{50,100,300};在ml-1m中取K1∈{100,300,500}。对于4个数据集,均设置输出特征的维数K2∈{30,50,100},神经网络隐层层数为1,激活函数为Relu。在K1与K2的不同组合下,表10至表13分别列出了数据集sushi、jester、ml-100k和ml-1m在LMaFit+DMF经过1 000次迭代之后的实验结果。 从表10至13可以看出:在给定K1时,不同的K2对应的损失函数值以及评价指标值相差较小。当K2固定且K1增加时,表10、表12和表13的损失函数值有明显的下降趋势,而表11的损失函数值先增加再降低;表11的所有评价指标均先递增再递减;表10、表12和表13的训练误差呈递减趋势;表10的测试误差先减后增,表12的测试误差单调递增,表13中测试集的RMSE单调递减而MAE先减后增。综上,K1的选取对LMaFit+DMF的实验结果更加敏感,故选取合适的K1是非常重要的。此外,对某些数据集而言,较小或较大的K2对测试误差不利。 表10 数据集sushi下不同特征维数的实验结果 表11 数据集jester下不同特征维数的实验结果 表12 数据集ml-100k下不同特征维数的实验结果 表13 数据集ml-1m下不同特征维数的实验结果 接下来考虑4个数据集分别在激活函数Sigmoid、Tanh、Relu和Softplus下的误差。通过比较表10至表13,取数据集sushi、jester、ml-100k和ml-1m的K1值分别为80、80、100、500,K2值分别为50、100、50、50。图2至图5绘出了4个数据集在不同激活函数下经过1 000次迭代的训练集的RMSE曲线。 观察图2至图5,可以得出如下结论。当迭代次数较小(epoch<200)时,4种激活函数对应的训练集的RMSE有较大的区别,Softplus均取得最小误差,而Relu却表现出较差的性能。对于较大的迭代次数(epoch>800),图2中的4条曲线比较接近,Tanh、Relu和Softplus对应的3条曲线几乎重合,且优于Sigmoid;图4中Relu的误差最小,且明显优于其他3个激活函数;图5中Relu也取得最佳性能。这些结论表明Relu是4个数据集中最适合的激活函数,且该函数运算简单,计算速度较快。 图2 sushi在不同激活函数下训练集的RMSE 图3 jester在不同激活函数下训练集的RMSE 图4 ml-100k在不同激活函数下训练集的RMSE 图5 ml-1m在不同激活函数下训练集的RMSE 最后,在激活函数Relu下比较神经网络隐层层数N对推荐性能的影响。当N比较大时,算法的计算复杂度和存储复杂度均比较大,故文中只考虑了较小的层数,即N∈{1,2,3,4}。在sushi等4个数据集上进行实验,图6至图9绘出了训练集的RMSE曲线。类似地,对于较小的迭代次数,N=1与其它隐层数的训练误差有显著区别。当迭代次数较大时,图7、图8中的4条曲线几乎重合,图6、图9中的4条曲线比较接近。由于隐层层数为1的神经网络模型的计算复杂度最低,所以在文中给定的实验设置下,隐层层数N=1是最佳的选择。 图6 sushi在不同隐层下训练集的RMSE 图7 jester在不同隐层下训练集的RMSE 图8 ml-100k在不同隐层下训练集的RMSE 针对传统矩阵分解中两个隐特征向量,使用两个多层感知器和双线性池化算子来替代双线性映射,通过最小化正则化的损失函数来获得隐特征向量和网络参数。为了便于求解所建立的深度矩阵分解模型,基于两阶段法设计了求解算法:先使用LMaFit确定隐特征向量,再使用神经网络技术求解网络参数。在真实数据集上的实验结果表明,笔者提出的深度矩阵分解具有最小的测试误差,比其他的深度分解方法在运行时间上更具有优势。 在今后的研究中,联合优化或交替优化深度矩阵分解的模型变量将是值得研究的方向。1.2 深度矩阵分解
2 新型深度矩阵分解模型
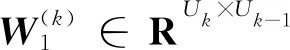
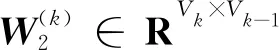
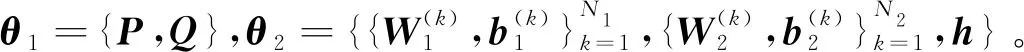
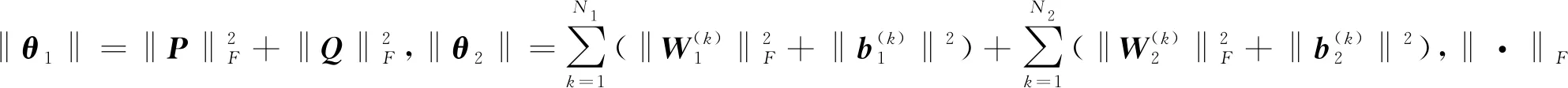
3 模型求解
3.1 θ1的确定
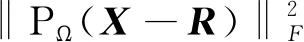
3.2 θ2的更新
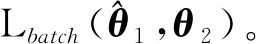
4 实验结果与分析
4.1 实验描述与实验设置
4.2 与其他推荐方法的对比



4.3 优化器的选择




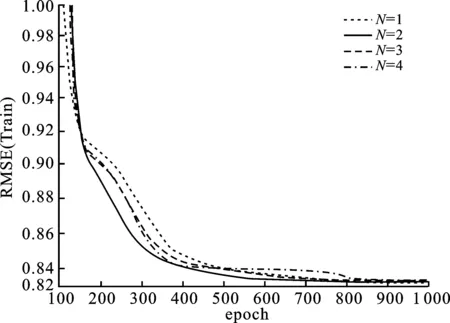
4.4 参数对LMaFit+DMF的影响
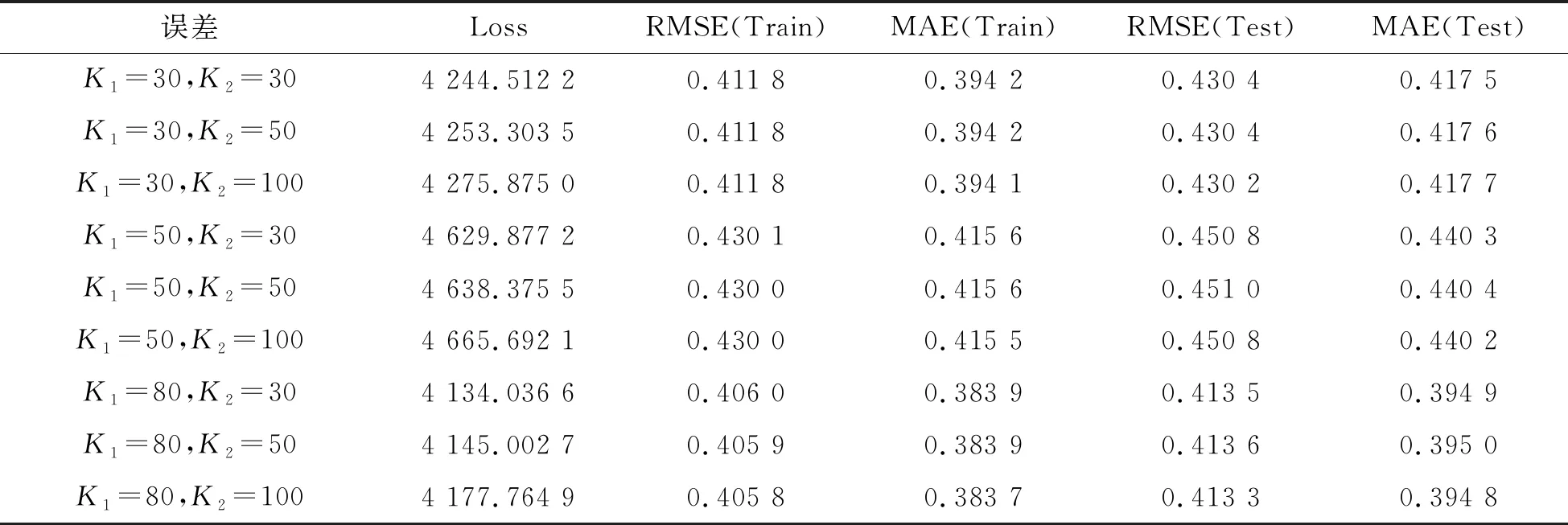
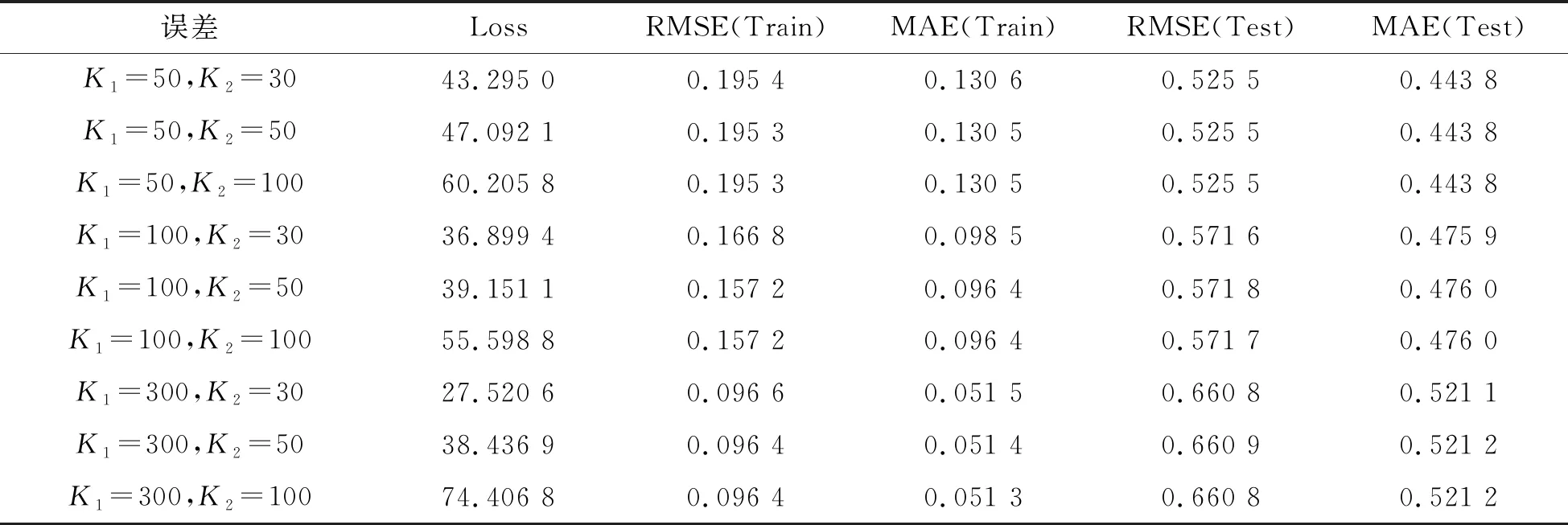
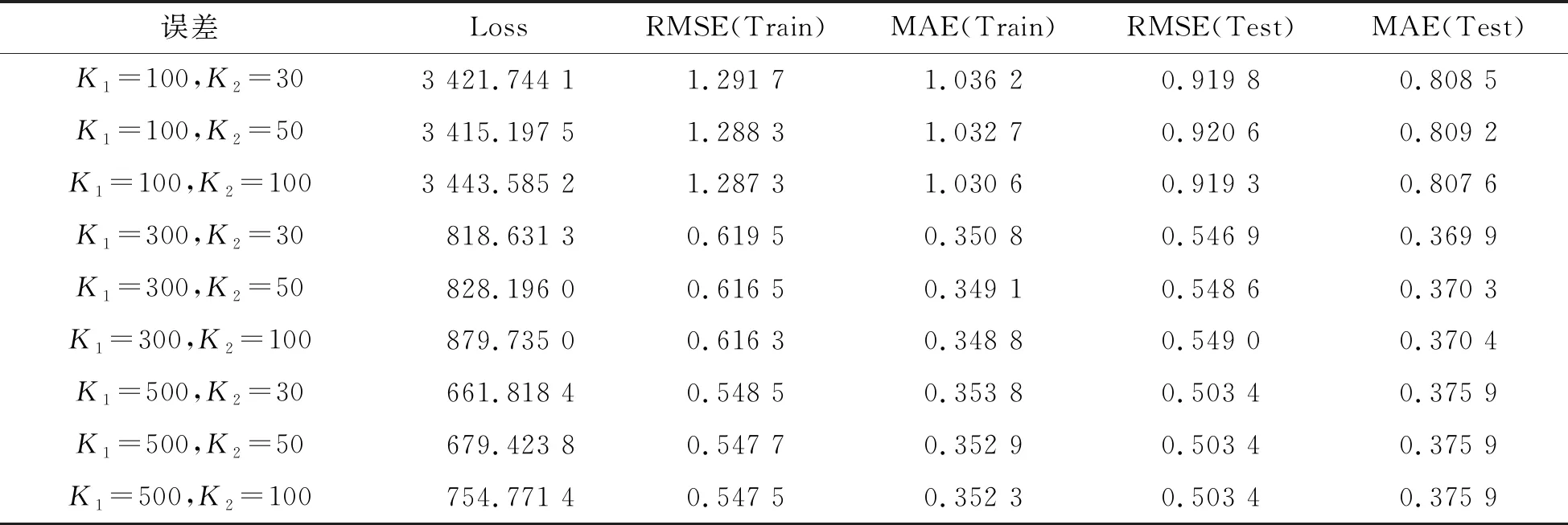
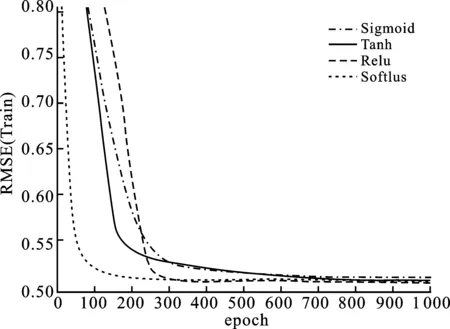
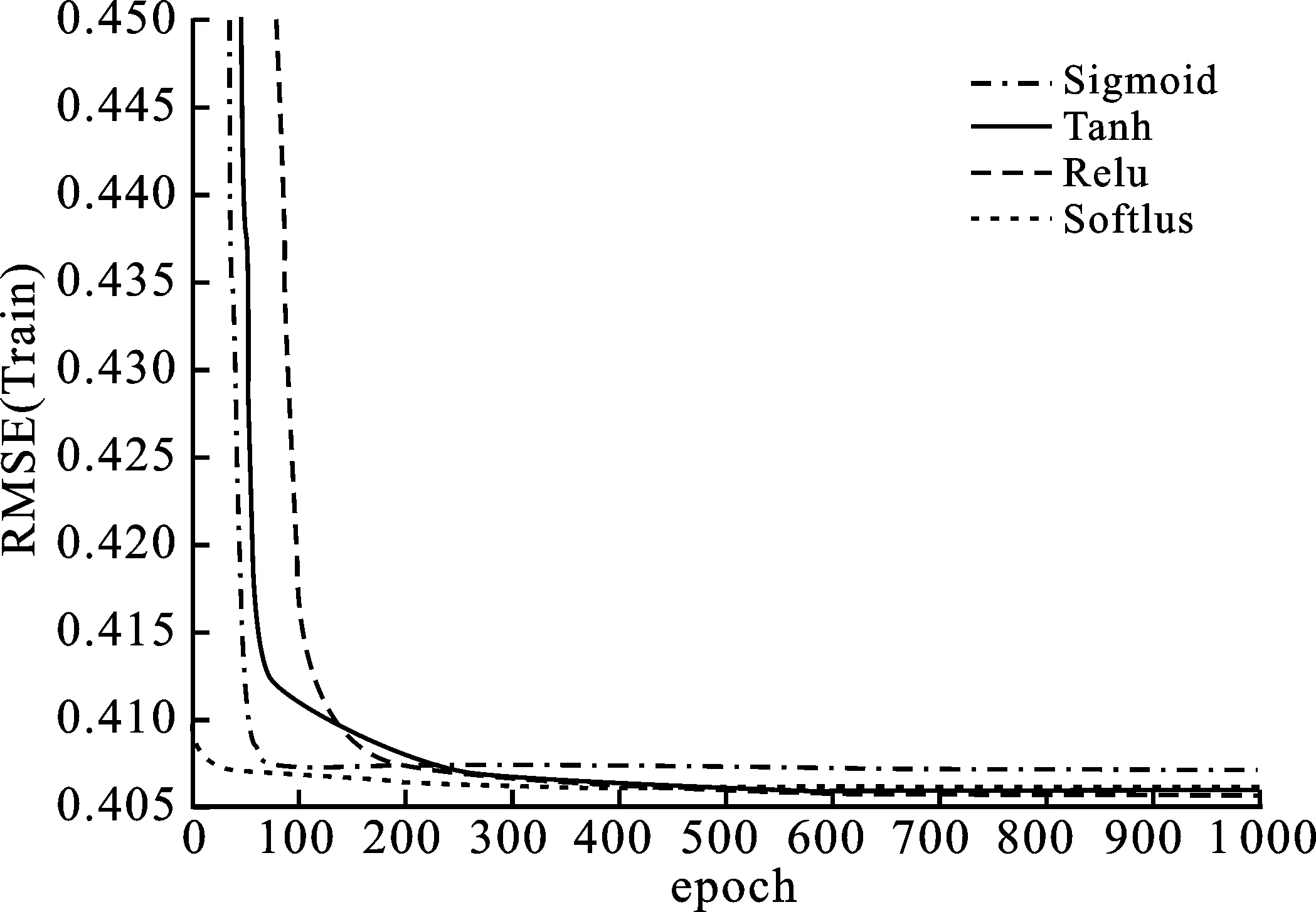
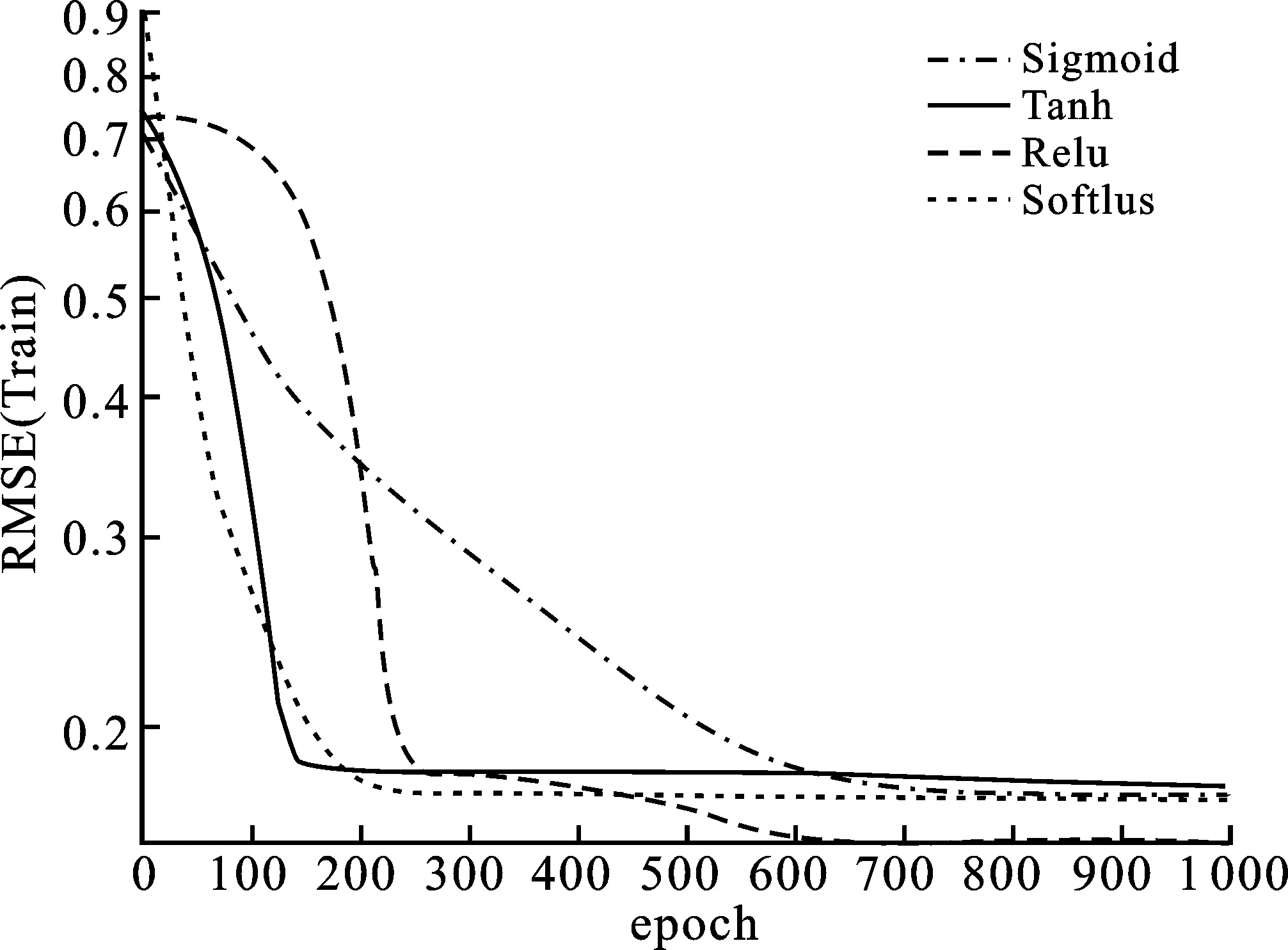
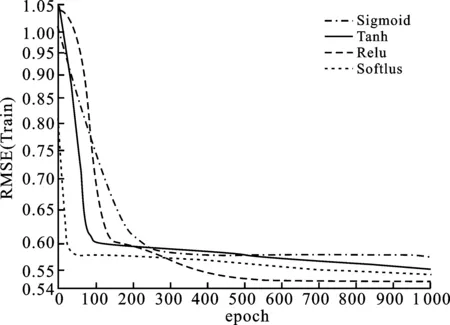
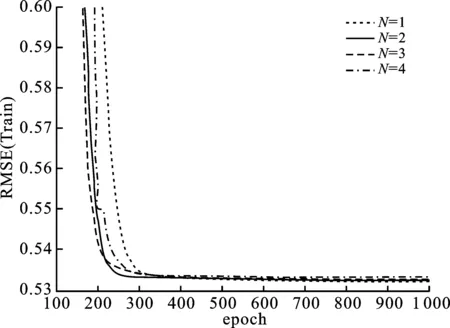
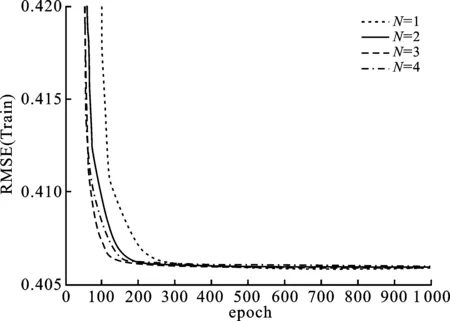
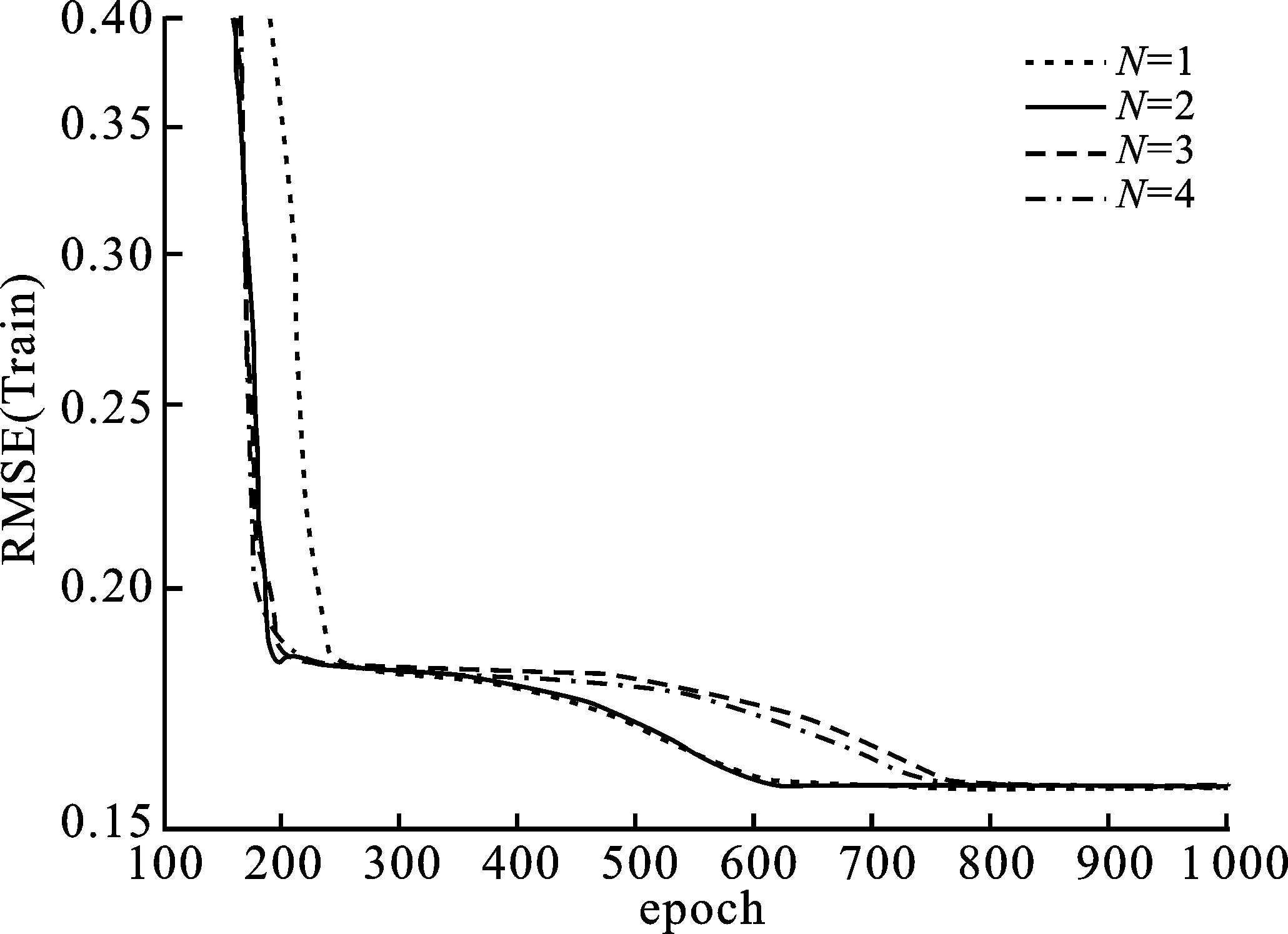
5 结束语

