融合项目属性偏好的矩阵分解推荐模型
韩立锋,陈 莉,史晓龙
(1.西北大学 信息科学与技术学院,陕西 西安 710127;2.西安电子科技大学 计算机科学与技术学院,陕西 西安710126)
伴随着传统PC互联网以及移动互联网的高速发展,电子商务已经渗透到生产生活的各个方面,为人们的生产生活带来了极大便利。然而,电子商务在给人们带来机遇的同时,也面临着很大的挑战。特别是随着电子商务的高速发展,无论是商家还是用户,都面临着信息过载的困扰。用户希望能够在尽可能短的时间内在海量的商品信息中获取自己喜欢的或者感兴趣的商品,而商家则希望使用最高效的方式帮助用户找到自己喜欢的商品。
为了解决这类问题,个性化推荐系统应运而生。所谓个性化推荐系统,旨在根据用户的历史消费喜好预测用户对未知产品或服务的偏好,进而为用户推荐合适的产品或服务,提高用户的满意度[1-2]。
目前,在个性化推荐领域,使用最为广泛的推荐算法是基于协同过滤的推荐算法。而协同过滤算法是基于集体智慧的思想,无论是基于记忆的协同过滤,还是基于模型的协同过滤,其主要思想都是通过用户对于商品的历史购买记录来帮助用户寻找自己可能喜欢的商品。目前基于协调过滤的推荐算法已经被广泛应用于个性化电子商务推荐、新闻推荐、音乐推荐等诸多领域[3-5]。
基于协同过滤的推荐算法被证明在实践中有着很好的效果,可以分为基于内存的协同过滤[6]以及基于模型的协同过滤[7]两类算法,目前被广大学者持续研究。BOBADILLA等[8]提出了一种新的协同过滤度量方式,将MSD和Jaccard度量结合起来,可获得更好的精度。LIU等[9]提出了一种新的用户相似性模型,该模型不仅考虑了用户评级的局部上下文信息,而且考虑了用户行为的全局偏好。此外,改进的相似性度量模型不仅考虑了两个用户之间的公共评级比例,同时也考虑到不同的用户有不同的评级偏好。实践证明,该模型具有很好的预测精度。LI等[10]提出新的跨域协同过滤推荐模型,将CF域视为一个二维站点时间坐标系,在这个坐标系上,多个相关域共享多个相关CF域的公共评级知识,以提高CF的性能。
然而,面对数据稀疏、冷启动等一系列问题,基于记忆的协同过滤算法无法准确地计算出物品与物品、用户与用户之间的相似度,进而无法为用户推荐准确的商品。特别是对于大多数新用户来说,因其较少的历史购买记录,甚至根本没有相关购买记录或评分记录,所以无法为其寻找其最近邻用户,从而影响推荐的准确性。针对此类问题,国内外学者进行了深入的研究:传统的基于内存的协同过滤技术在面临数据稀疏、冷启动问题时遭遇推荐瓶颈,其最主要原因在于传统的基于记忆的协同过滤技术只是过度关注用户或项目的近邻,而忽视了用户或项目本身,同时也忽略了两种实体之间的关联。所以基于此,国内外学者在协同过滤推荐算法的基础上提出了一种新的基于模型的协同过滤——矩阵分解算法(Matrix Factorization,MF)。矩阵分解算法的核心思想是用户的特征矩阵与项目的特征矩阵都可以表示为低维的特征向量,而用户的评分则可以用此二者之特征向量的内积表示。尽管大量的矩阵分解算法能够将用户与项目的信息进行充分挖掘,从而提高推荐效果[11],但对于评分较少的冷用户信息,依旧无法有效挖掘。此时,越来越多的辅助信息被加入到矩阵分解框架之中,比如人口统计学信息、社会化网络信息、项目描述信息等,在一定程度上提高了推荐精准度,同时对于冷启动用户的推荐效果也有所提升。比如MANZATO[12]提出了一种基于用户偏好与电影类型/类别的分解矩阵的推荐算法。使用这种用户类型矩阵分解模型的优点是需要较少的计算资源,矩阵的稀疏性更小,维数更低,推荐准确性更高。为了解决用户项目评价模型的极大稀疏性,QIN等[13]提出了一种基于加权项目类别的协同过滤推荐算法,该算法将用户物品的高维评价数据转化为用户类别的低维统计数据,并作为用户特征模型。在模型的基础上,加入遗忘功能和用户属性信息,对用户模型进行两次优化。实验结果表明,该模型能够较好地应对用户物品评级问题的稀疏性,同时较好地解决冷启动问题。
上述算法以矩阵分解为基础,同时融合更多其他辅助信息,对于应对冷启动问题有显著的效果。尽管目前深度学习算法已被大量应用于个性化推荐领域,并且也取得了一些成绩。然而,目前的研究主要聚焦于探索应用于个性化推荐而提出新的深度学习架构上,比如注意力机制、卷积神经网络、生成对抗网络、图神经网络等[14-17]。尽管取得了一定的效果,但这些依赖于复杂网络结构的工作有大量的参数,需要耗费更多的计算资源,同时在可扩展性以及可解释性等方面也存在一定的问题。所以,笔者采取以矩阵分解为基础的推荐模型,同时考虑用户、商品属性信息,考虑用户对物品属性的偏好信息等,最终对于冷启动用户进行项目评分的预测,取得了较好的结果。
笔者的贡献主要包括:
(1) 在进行用户相似度计算时,融合了用户本身信息,包括年龄、性别、职业等,以及用户对于项目偏好的信息,即用户对于项目属性偏好的差异。进行相似度计算后,进行了比较粗略的评分预测,并将这一结果融入到新的矩阵分解之中。
(2) 根据用户相似度,计算出冷启动用户对项目的初始预测值,同时在进行矩阵分解时,融合用户的属性信息、用户对项目属性的偏好信息、项目属性信息等,作为辅助信息对矩阵分解的隐类分解起到增强作用,更能提高最终冷启动用户的推荐效果。
(3) 在数据集movielens及douban上进行了大量实验。实验表明,笔者给出的模型与现有矩阵分解模型相比,有更好的推荐准确性以及可扩展性。
1 相关工作
在基于用户的协同过滤推荐中,评分信息是一个m×n阶矩阵,m行代表m个用户,n列代表n个项目。第i行第j列的元素值代表用户i对项目j的评分。评分值一般是1~5之间的整数。评分越大,表示用户越喜欢该项目。用户项目评分数据矩R的各元素阵如表1所示。
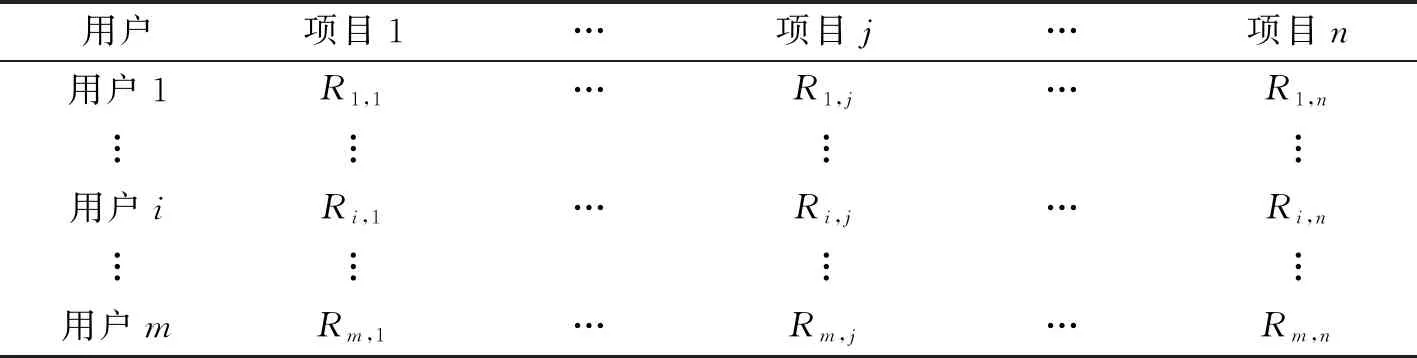
表1 用户项目评分矩阵
1.1 基于用户的K最近邻算法
K最近邻(K-NearestNeighbor,KNN)分类算法是最著名的数据挖掘算法之一[18-19],早期被应用于文本分类研究中,取得了非常好的分类效果。随着个性化推荐技术的流行,K最近邻作为非常重要的基于领域的协同过滤方法,也被广泛应用。在个性化推荐领域,K最近邻又被分为基于用户的K最近邻以及基于项目的K最近邻。它们的核心都是计算相似度[20]。
在相似度计算中,常见的有余弦相似度、相关相似度等计算方式。余弦相似性假设用户u,v在N维项目空间上的评分分别表示为向量u和v,则用户u,v之间的相似度Ssim(u,v)就是两个向量夹角的余弦值,其计算公式如下:
(1)
要进行相关相似度计算,首先假设用户u,v同时评过分的集合为I,则用户u,v之间的Ssim(u,v)可通过皮尔逊系数进行计算。皮尔逊相关系数正好用于衡量变量与变量之间的线性关系,目前也是推荐系统较为广泛的相似度度量方法。其计算公式如下:
(2)
通过计算用户之间的相似度,选取与目标用户u最近的k个邻居集,对项目j进行评分预测:
(3)

1.2 矩阵分解
随着Yehuda Koren在Netflix比赛中取得了冠军成绩后,基于矩阵分解的个性化推荐模型得到研究者的广泛关注[21-24]。作为协同过滤技术的一种,矩阵分解技术属于一种隐语义模型。与传统协同过滤方法不同的是,矩阵分解并不通过计算相似度来查找相似用户或项目,进而进行预测。相反,矩阵分解根据其数学理论基础奇异值分解,认为一个实矩阵R可以分解为3个矩阵U、Σ和V的积[25]:
(4)
在个性化推荐中,研究者认为:可将评分矩阵近似表示为用户隐特征矩阵及项目隐特征矩阵的乘积,从而对用户和项目进行建模,如图1所示。

图1 推荐系统评分预测模型
由于评分矩阵非常稀疏,通常将原始矩阵近似为矩阵P和Q转置的乘积:
(5)

(6)
作为真实的评分值和预测评分值之间的差距,可以用下式定义损失函数:
(7)
其中,D是所有评分后的用户和项目集,即训练集中的用户和项目;而λ是控制正则化参数,防止过拟合。
2 融合属性信息的矩阵分解
近年来,基于矩阵分解的个性化推荐得到了广泛的研究和应用,也取得了较好的效果。但是矩阵分解存在较为严重的冷启动问题,即对于特别稀疏的评分矩阵,尤其是对于评分较少的冷启动用户,无法根据现有信息对用户进行深入挖掘,所以便无法进行精准评分预测,从而无法为冷启动用户进行相关推荐。为了避免此类问题发生,越来越多的矩阵分解模型加入了诸如社会化网络、异构网络等信息,取得了更好的效果。在上述研究方法的启发下,基于用户属性与项目属性构建评分矩阵,笔者进行冷启动用户的初始评分预测,同时融合用户对项目属性的喜好构建用户兴趣矩阵、用户属性信息、项目属性信息,将此类信息源融入现有的矩阵分解模型之中,以期取得更好的推荐效果,如图2所示。

图2 算法框图
首先对冷启动用户基于其用户属性信息和已经观看的电影类型信息进行建模,得到其近邻集,根据K最近邻算法得到冷启动用户的初始预测评分。其次,针对于已有用户对其根据用户属性、项目属性、用户对项目属性偏好信息进行矩阵分解建模,学习各相关参数。然后对冷启动用户使用矩阵分解建模,结合矩阵分解模型中已有的用户评分信息、项目属性信息、用户对项目属性的偏好信息所学习到的各种参数,融合冷启动用户初始评分预测信息,进行全局范围的参数更新,最终得到新的评分矩阵,从而为冷启动用户进行更为精准的评分预测。最后对冷启动用户进行相关项目推荐。
2.1 融合用户属性与电影流派信息的评分预测模型建立
对于冷启动用户,相互之间进行共同评分的项目较为匮乏。此时,首先基于用户性别、年龄、职位等用户人口统计学信息,对其进行相似度计算。其次,虽然冷启动用户的共同评分较少,但是对于有过评分记录即使评分记录不多的冷启动用户,可以同时基于项目视角,根据项目属性相似度,计算冷启动用户与其他用户之间的相似度。最终形成冷启动用户的推荐列表。
要基于用户人口统计学信息进行用户间相似度计算,可对这些信息按照一定标准进行数值化处理。比如,对于性别,按照男(M)女(F)作为划分标准,使用数字1、0代替。对于职业信息,根据我国职业分类标准,用数字1~7代替。对于年龄信息可以根据年龄段进行处理,根据生物学年龄划分标准,用数值1~7代替。处理后的人口统计学信息如表2所示。

表2 处理后的用户人口统计学信息
对以上信息可根据下式进行归一化处理:
(8)
接着,进行用户之间相似度计算:
Ssimr(u,v)=αS(u,v)+βA(u,v)+(1-α-β)O(u,v) ,
(9)
其中,S(u,v)为性别相似性,A(u,v)为年龄相似性,O(u,v)为职位相似性。在进行上述属性相似性计算时,可以使用余弦相似性计算方式。参数α、β、(1-α-β)分别代表性别、年龄、职位相似性的权重。根据实验得知,当α、β、(1-α-β)各参数值为{0.6,0.1,0.3}时,所得到的相似度是最准确的。
以上步骤描述了基于用户人口统计学信息进行相似度计算的过程。但是对于已经有过评分记录的冷启动用户来说,仅仅基于用户特征计算相似度,而忽略用户本身与其他用户在项目类型之间的相似度,往往不能精准全面地分析用户行为。以电影为例,流派信息作为电影最为重要的类型信息,用于区别电影之间的不同。电影根据流派进行划分,可以被划分为16个流派:犯罪、浪漫、动作、喜剧、科幻、戏剧、幻想、黑色、纪录片、恐怖、惊悚、儿童、战争、动画、悬疑、冒险。假设用户A、B的历史观看记录中,表明两者都喜欢观看具有动画、儿童、喜剧流派特征的电影,则表明两者具有很大的相似性。如果A用户已经观看了电影《Toy Story (1995)》,则系统也可以将该电影推荐给用户B。
根据这一思路,可以融合电影流派相似度计算用户相似度。在评分矩阵R中,包含了用户U、项目I,其中U={u1,u2,u3,…,um},I={i1,i2,i3,…,in},rui表示用户u对项目i的评分。项目i的流派属性集合G(i)={g1,g2,g3,…,gs}。假设项目i中具有该流派属性,则gi为1;否则,gi为0。设用户u看过的电影集合为Iu,则用户u对于电影流派属性gi的累加次数为
(10)
其中,gix表示在所有该用户看过的电影Ix中流派属性gi的累计次数。
假设对于固定电影项目I,共有m个流派属性,根据式(10)可以得到某用户u对于各项目流派属性的偏好,记做Lui,则用户u对于m个流派属性的偏好可表示为(Lu1,Lu2,…,Lui,…,Lum)。此时,可以根据式(11)计算用户u与用户v基于项目属性的相似度:
(11)

用户之间的最终相似度为
Ssim(u,v)=λSsimr(u,v)+(1-λ)Ssimarr(u,v) ,
(12)
其中,Ssimr(u,v)表示用户u与用户v的人口统计学属性相似度,simarr(u,v)表示用户u与用户v基于电影项目流派属性喜好视角的相似度值,参数λ则表示各自的权重。
此时,可根据最终相似度寻找用户u的最近邻集,然后根据评分公式得到项目评分。算法如下。
算法1融合用户属性与电影流派信息的K最近邻算法。
输入:用户评分矩阵UImatrix,用户属性矩阵UAmatrix,项目流派属性矩阵IAmatrix,邻居个数K。
输出:预测后的用户评分矩阵UImatrix′。
算法过程:
① 初始化评分矩阵UImatrix,相似度列表SimilarList,用户评分UserPreference
② foru∈Unewdo
③ 使用式(11)得到用户u相似度列表SimilarList
④ 通过对SimilarList进行排序,得到用户u的前K个近邻集Neighbor
⑤ foru∈Neighbor do
⑥ 根据式(3)得到用户u的预测评分值UserPreference
⑦ end for
⑧ end for
⑨ 更新评分矩阵UImatrix′
⑩ 返回评分矩阵UImatrix′。
2.2 基于项目属性信息的用户偏好模型建立
大量的心理学、营销学理论表明,人们对于商品的偏好很大程度上依赖于对该商品所对应属性的偏好。对于电影本身来说,其具有电影类型、年代、地区等重要属性信息。对于每个属性,也具有不同的属性值。假设某用户的项目评分记录如表3所示。

表3 项目属性信息
根据表3,假设ui表示第i个用户;项目属性集可以表示为A,共有m个属性。每个属性均有不同的属性值,比如电影类型有浪漫、动作、喜剧等16种取值;地区有美国、英国、日本等;年代有80年代、90年代等。项目属性集可以表示为C={a11,…,a1d,a21,…,a2k,…,am1,…,amn},amn表示项目中的第m个属性的第n种取值。如果该项目中具有该属性值,则为1;否则,为0。项目属性矩阵可以表示为
此时,可计算用户u对于某属性值的偏好程度,计算公式如下:
(13)
其中,Cij表示用户u对项目中第i个属性中第j个值的偏好程度,比如可计算用户A对电影类别信息中名为动作片的偏好程度;NCountij表示该用户所观看电影集中该属性值的累计次数;z表示该用户所观看的电影数目。然而这种计算偏好的过程忽略了评分信息,用户u对第i个属性中第j个属性值最终偏好可以表示为
Tui=puiCuirui,
(14)
其中,pui表示某属性重要程度,Cui即为式(13)计算得到的属性值偏好,Tui则代表用户u对某属性值的最终偏好。根据这一思想,即可得到所有用户的属性偏好矩阵Zu。
2.3 融合属性信息的矩阵分解
矩阵分解技术因其简洁高效的特性,在个性化推荐领域占据着非常重要的地位,也被证明为效果优于传统基于用户协同过滤及基于项目协同过滤的经典算法。但在通常情况下,用户对于项目的评分矩阵也与用户与项目自身因素相关。比如有的用户习惯于给所有项目都给予较高的评分,而有的用户则恰恰相反;有的物品经常会被用户给予较高的评分,而有的物品则会被给予较低的评分。所以,为了使得评分更加精准,需要考虑用户和项目的偏置信息。新的预测函数和损失函数为
(15)
其中,μ代表全局平均分,bu代表物品评分偏置,bi代表用户评分偏置。通常可以使用梯度下降最优化方法进行求解,从而得到预测评分。
尽管上述矩阵分解方法得到了很好的效果,但是对于冷启动用户来说,其评分项目较为匮乏,更需要考虑项目属性信息及冷启动用户对已评分项目属性的偏好信息。此时用算法1中得到的新的评分预测矩阵UImatrix′得到r′,即冷启动用户根据用户相似度及所评分电影类型相似度共同计算出用户最终的相似度,从而找到该相似用户的最近邻,进而计算出冷启动用户对项目的初始预测值。在此基础上,融合用户的属性信息、用户对项目属性的偏好信息、项目属性信息等作为辅助信息,对矩阵分解的隐类分解起到增强作用,更能提高最终冷启动用户的推荐效果。图3为改进后的矩阵分解模型。

图3 改进后的矩阵分解模型

最终预测函数如下:
(16)
其中,r′表示初始预测评分,M表示用户属性集,其相关特征权重也可以通过已知评分矩阵学习得到。Z表示用户对项目属性偏好矩阵,其相关特征权重可以通过已知评分矩阵学习得到。G表示项目属性集,其相关特征权重也可以通过已知评分矩阵学习得到。
该评分预测函数的损失函数为
(17)
对应的参数更新公式如下:
(18)
具体算法见算法2。
算法2融合属性信息的矩阵分解算法。
输入:训练集用户评分矩阵Trainmatrix,训练集用户属性矩阵G(u),训练集项目属性矩阵G(i),用户对项目属性偏好矩阵Z,学习率α。
输出:预测后的用户评分矩阵UImatrix′、用户和项目特征矩阵P、Q,用户对项目属性偏好特征矩阵PF,项目属性特征偏好矩阵QF。
算法过程:
① 初始化bu、bi、P、Q、PF、QF、UImatrix′
② forrui∈Trainmatrix do

⑤ 利用随机梯度下降
⑥ 根据式(18)更新bu、bi、P、Q、PF、QF
⑦ 更新UImatrix′
⑧ 直到误差不再发生变化
⑨ end for
⑩ 返回参数列表bu、bi、P、Q、PF、QF
2.4 推荐列表生成
第1步 通过测试集用户项目评分矩阵用户属性矩阵项目属性矩阵等得到用户对项目属性偏好矩阵。
第2步 通过节2.3中的算法得到的bu、bi、P、Q、PF、QF等参数,结合用户评分矩阵、用户属性矩阵、用户对项目属性的偏好矩阵,在全局范围内利用梯度下降法更新bu、bi、P、Q、PF、QF等参数,直到误差不再发生变化。
第3步 根据第2步得到的最优参数进行非纯冷启动用户的项目预测评分。
第4步 对预测评分矩阵进行排序,选取top-N个项目推荐给非纯冷启动用户。
3 实验及结果分析
3.1 实验数据集及评价函数
由于推荐系统领域专门针对处理冷启动用户问题数据集并不多见,文中采用的是推荐系统领域内美国明尼苏达计算机学院的GroupLens小组提供的MovieLens中的ML-100K,ML-1M数据集,如表4所示。

表4 实验数据集
为了真实地模拟出非纯冷用户,在仿真实验中将用户数据分为70%的训练集,30%的测试集。对于每个测试集用户,随机选取5~10个项目作为其测试集项目。此时,测试集用户被模拟成为非纯冷启动用户。训练集用户的属性信息、训练集用户的评分信息以及通过计算得到的训练集用户对项目属性的偏好信息、训练集用户属性信息与电影流派偏好得到的预测评分矩阵信息作为输入数据。经过矩阵分解算法得到预测值,再经由实际值与预测值之间的差额逐步找到各个参数的最优值。而测试集用户被认为是冷启动用户,根据其用户属性信息与电影流派偏好得到的预测评分矩阵,同时融合其用户属性信息、用户对电影项目属性偏好信息,经过矩阵分解得到全局最优参数及评分预测值,最终形成推荐列表。
实验软件环境为:Windows10-64bits,Anaconda3、Python3.7。硬件环境为:CPU是英特尔 Core i7-8750H @ 2.20GHz 六核,内存为16 GB。
在推荐系统中,能够衡量推荐质量的标准很多,比如精度、召回率、F1度量等。用平均绝对误差(MAE)、均方根误差(RMSE)对推荐准确性进行评价。平均绝对误差也能够非常直观地度量推荐算法的准确性。平均绝对误差越小,推荐准确性越高。其定义为
(19)
其中,pu,i表示目标用户u对项目i的预测评分,Ru,i表示目标用户u对项目i的实际评分。而均方根误差为
(20)
3.2 实验结果与分析
通过以下实验,旨在解决如下问题:
(1) 文中算法中的不同参数对于实验结果的影响。
(2) 文中算法与其他算法比较在准确性方面的提升。
实验1 邻居个数K值对推荐准确性的影响。
通过K指定近邻项目的数量。为了验证K值对于推荐准确性的影响,分别选取MovieLens ML-100K,ML-1M两种数据集进行测试。对于第1种数据集,设K从3开始,逐步递增,步长为1,直到20结束。第2种数据集,设K从5开始,逐步递增,步长为5,直到100结束。观察不同K值下的平均绝对误差(MAE)及均方根误差(RMSE),实验结果如图4所示。

(a) ML-100K数据集中不同K值对MAE的影响
从实验结果可以得知,随着K值的增大,两个数据集均呈现了平均绝对误差及均方根误差先减后增的趋势。对于ML-100K数据集,当K=10时,平均绝对误差、均方根误差达到最小值,此时得到最佳的推荐性能。对于ML-1M数据集,当K=38时,得到最佳的推荐性能。
实验2 参数λ对推荐准确性的影响。
参数λ控制着正则化项的程度,对于推荐准确性也有很大的影响。现将λ从0.01增加至0.20,并保持其他参数不变,实验结果如图5所示。

(a) ML-100K数据集中不同λ值对MAE的影响
从图5中可以看出,随着参数λ的变化,平均绝对误差与均方根误差也随之变化。这是因为当参数λ变化时,其赋予模型中属性的权重也随之变化,过大或者过小,都会影响最终的预测效果。在ML-100K数据集中,当λ=0.20时推荐性能最优;而在ML-1M数据集中,当λ=0.15时,推荐性能最优。
实验3 迭代次数对推荐准确性的影响。
为了验证文中算法的平均绝对误差、均方根误差随着迭代次数变化的情况,在ML-1M数据集中,假定正则化参数λ=0.15时,试验结果如图6所示。

(a) ML-1M数据集中迭代次数对MAE的影响
从图6可以观察到,当迭代次数小于200时,推荐效果较差。随着迭代次数的不断增加,推荐效果趋于平缓。当迭代次数等于250时,推荐效果最优。
实验4 不同算法的性能比较。
为了验证笔者提出的算法,通过选取以下4种算法进行比较。
传统矩阵分解算法(SVD):算法假设用户对项目最终评分在很大程度上取决于用户和项目的潜在属性。通过将评分矩阵分解为2个低秩的用户项目矩阵,即用户隐特征矩阵P以及项目隐特征矩阵Q,降低了矩阵维度。
SVD++:由KOREN[26]提出,在进行评分预测时,同时考虑了用户、物品的偏置信息。
PMF:由SALAKHUTDINOV等[27]提出的基于概率矩阵分解的个性化推荐算法。
CBMF:该方法由NGUYEN等[28]提出,将内容信息直接整合到矩阵分解方法中,以提高推荐的质量。
FSVD:由GUO等[20]提出,该算法将项目属性信息和评分信息进行有效结合,较好地解决了冷启动问题。
为了验证笔者提出算法的有效性,假定用户和项目因子固定不变,且正则化参数λ的值保持一致,观察各算法的平均绝对误差在ML-1M数据集中随迭代次数变化的情况。实验结果如图7所示。
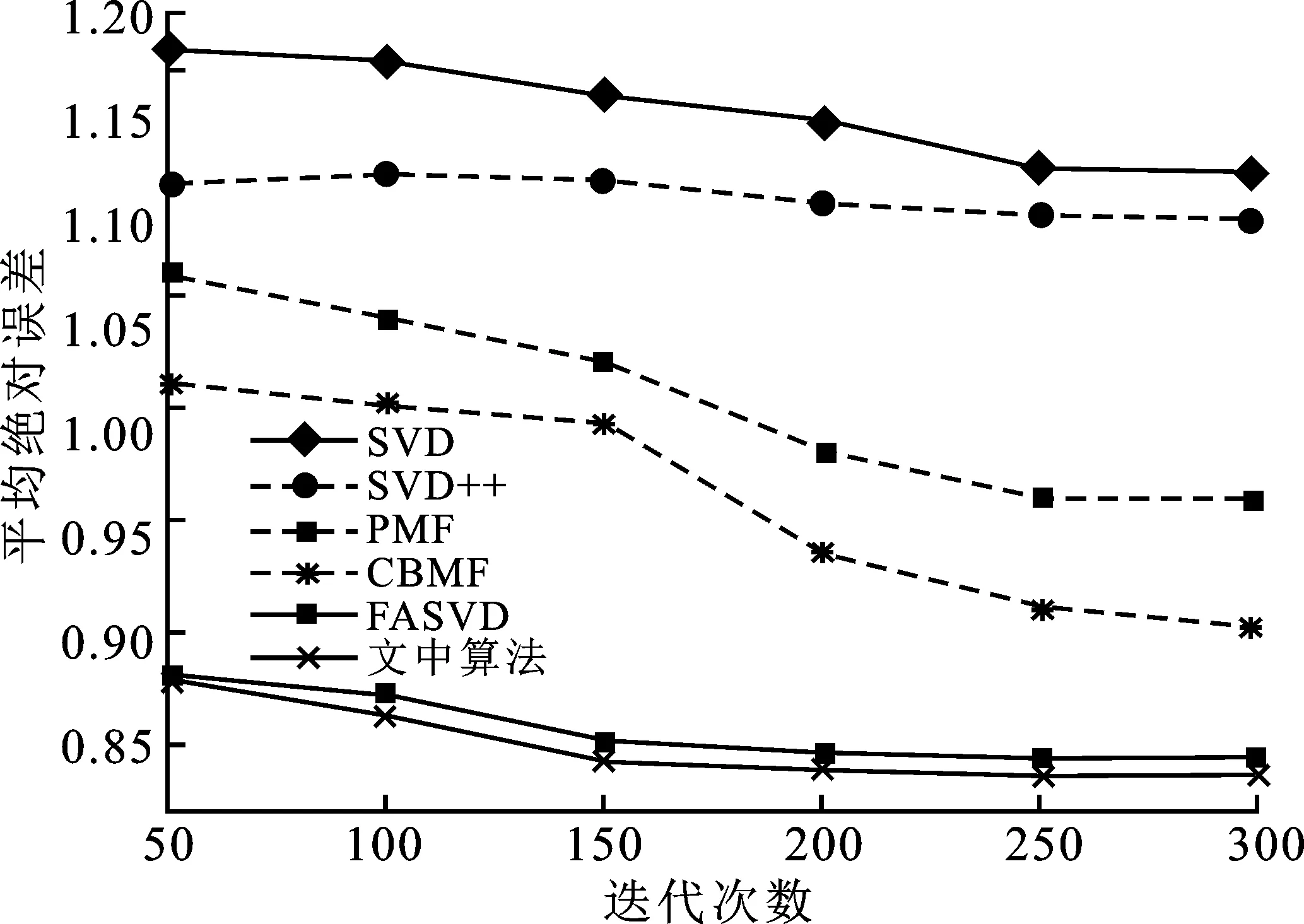
(a) ML-1M数据集中各算法随迭代次数变化的MAE值
从图7中可以看出,当矩阵分解算法在迭代次数大于250次时,趋于稳定;SVD++则一直处于比较平稳的状态,平均绝对误差随着迭代次数呈较为平缓的下降趋势。PMF算法则刚开始一直处于比较急剧的下降状态,当迭代大于200次时,平均绝对误差达到最低,且趋于平缓。FASVD算法和文中算法在刚开始时,呈下降趋势,当迭代次数大于250时,呈平稳趋势,且在迭代次数等于250时,平均绝对误差达到最低,推荐效果最优。均方根误差也有同样效果的表现。同时,可以看到文中算法在与其他算法进行比较时,在推荐准确性方面均优于其他算法。
实验5 可扩展性验证。
为了验证文中算法的可扩展性,选取了Douban Movie数据集作为验证。实验通过设置邻居个数K值以及迭代次数,来研究文中算法在其他数据集上的性能表现。图8记录了最终实验结果。
从图8(a)中可以看出,当K值发生变化时,平均绝对误差值也随之发生变化。当K小于55时,平均绝对误差呈下降趋势;当K值等于55时,平均绝对误差达到最小值,推荐效果最优,随后又平缓增加。而图8(b)则表明,随着迭代次数的增加,系统模型趋于稳定。当迭代次数等于250时,推荐效果最优。

(a) Douban Movie数据集中不同K值对MAE的影响
4 结束语
在传统矩阵分解的基础上,笔者充分考虑了用户属性信息、项目属性信息、用户对项目类型偏好信息,对矩阵分解中隐类信息的分解起到了增强作用。同时使用冷启动用户基于用户属性及所评项目类型得到近邻集,从而计算出冷启动用户的初始评分预测值,替代在矩阵分解中的全局平均分,更能逼近冷启动最终真实评分值。通过与其他算法进行比较,表明笔者提出的算法在推荐准确性方面有一定的提升。同时,在扩展性方面,也具备了一定的优势。事实证明:笔者提出的算法在数据较为稀疏的情况下,充分考虑用户属性信息、项目属性信息、用户对项目类型偏好信息,能较好地解决用户冷启动问题,同时提高了推荐准确性。但是对于用户属性和项目属性,其有着更为丰富的内容,且用户和用户、项目和项目、用户和项目之间都存在某种程度的关联。如何将这些信息加以考虑,对算法进行更深层次的优化,是未来研究的重点,也是需要进一步改进的方向。

