一阶一致性收敛速率的拓扑优化方法综述

2022-07-04 03:20陈新庄郭志伟李江荣

延安大学学报（自然科学版） 2022年2期

陈新庄，郭志伟，李江荣

（1. 延安大学数学与计算机科学学院，陕西延安 716000；2. 西北工业大学数学与统计学院，陕西西安 710072）

多智能体系统是分布式人工智能领域的前沿和研究热点，在传感器网络［1］、智慧电网［2］、智能交通［3］、机器人［4］、数据网络［5］、分布式计算［6］、航空航天［7-9］等多个领域都有重要的应用。在多智能体系统的研究中，一致性问题［10-13］是研究其他分布式协同控制问题的基础，受到国内外学者的广泛关注和深入研究。

多智能体系统一致性协议的收敛速率，决定了多智能体系统从初始状态达到一致的快慢，是一致性协议的重要性能量化指标。为了提高多智能体系统达到一致性的收敛速率，通常从改进一致性协议和优化通信拓扑2个方面进行研究。早期的一致性协议是渐近收敛的，为了提高多智能体系统达到一致的收敛速度，大量学者对一致性协议进行了深入研究并进行了持续的改进，设计了有限时间收敛［14］和指定时间收敛［15］的一致性协议。然而，相比于控制协议，从网络拓扑角度对收敛速度的研究相对滞后，很多问题依然没有有效解决。

当多智能体系统的一致性协议给定时，收敛速度是由多智能体系统的通信拓扑的特征值决定的［11-13］。例如，一阶多智能体系统在渐近收敛的一致性协议下［11-12］，当通信拓扑为无向图时，系统的收敛速度由网络拓扑的代数连通度［16］（拉普拉斯矩阵的第二小特征值）决定，代数连通度越大，收敛速率越高。对高阶多智能体系统，一致性通常由网络拓扑的代数连通度和谱半径（拉普拉斯矩阵的最大特征值）共同决定，代数连通度越大、谱半径越小，系统的一致性收敛速度越快［17-18］。受智能体个体通信能力、通信范围和环境等约束，往往无法让任意2个智能体间都进行通信。如何在给定的限制条件下设计网络或优化已有网络，使得一致性收敛速率最高，是非常有意义的问题。

一阶连续多智能体系统是最简单的一类多智能体系统，即所有的智能体的状态是关于时间的连续函数，且动力学是一阶积分器模型。连续模式的一致性协议设计了理想情况下系统达到一致的控制算法。然而，由于受通信硬件、通信带宽和计算能力等限制，智能体间无法在短时间进行无数次通信。因此，学者们开发了周期采样和事件触发模式的一致性协议［19-22］，减少了智能体间的通信量，降低了系统通信的要求，让多智能体系统的工程应用成为可能。在保证收敛的前提下，这三类一阶一致性协议的收敛速率由通信拓扑的代数连通度决定的。优化调整通信拓扑结构，是提高多智能体系统一致性收敛速率的有效方法。学者们对代数连通度的最大化进行了大量的研究。由于代数连通度最大化问题是NP-难问题［23］，若同时考虑各种约束和限制，问题会更加复杂。

针对通信拓扑为无向图的一阶多智能体系统，将在第二节介绍连续、周期采样和事件触发模式的一致性协议及其收敛速度。第三节针对以提高收敛速率为目标的代数连通度最大化问题，对当前采用的方法进行分类总结。最后，针对多智能体系统收敛速度和通信量的优化，提出了当前可进一步研究的若干问题。

1 多智能体系统的拓扑建模及图论基本知识

一个包含n 个智能体的多智能体系统，其通信拓扑用图论中的图进行建模。单个智能体i用图中的顶点vi表示，两个智能体之间的通信用图中的边表示。若智能体i和智能体j能相互通信，则用图中的无向边vivj表示其通信关系；若智能体i能接收到智能体j的信息，但是智能体能j不能接收到智能体i的信息，则用图中的有向边(vj，vi)表示其通信关系。本文仅考虑多智能体系统通信拓扑为简单无向图的场景，即所有通信的智能体进行双向通信。

令G =(V(G)，E(G)) 是一个无向图，其中V(G) ={v1，…，vn}表示图G 的顶点集合，E(G)表示图G 中边的集合。如果图G 的每一条边vivj都赋予一个非负权值wij，则称图G 为赋权图。非赋权图可以看作边上权值为1的特殊赋权图。Ga是一个非赋权简单无向图，图Gb是与Ga有相同边集的赋权无向图。如果v是图G 的顶点，那么将v及其与之关联的边都删除得到的图记作G - v。如果vivj是图G 的一条边，那么将这条边删除得到的图记作G - vivj；否则，将边vivj添加到图G 得到的图记作G + vivj。图论相关的符号和定义，参考图论教材［24］。

假设图G 是一个赋权图，其邻接矩阵A(G) =[auv]∈Rn×n定义为：如果uv ∈E(G)，则aij= wij，否则aij= 0。令Ni={vj|vivj∈E(G)}表示顶点vi的邻居集合。图G 中顶点vi的赋权度定义为di=令D(G) = diag(d1，…，dn)为顶点的度构成的对角矩阵，则图G 的拉普拉斯矩阵为L(G) =D(G) - A(G)。为了简化描述，图G的拉普拉斯矩阵L(G)的特征值λk(L(G))或特征向量uk(L(G))简称为图G的特征值λk(G)或特征向量uk(G)。

由于无向图G 的拉普拉斯矩阵L(G)是半正定的实对称矩阵，其特征值可以按照非递减的顺序排列为λ1(G) ≤λ2(G) ≤…≤λn(G)，其中λ1(G) = 0且对应的特征向量为1。图G 的第二小特征值λ2(G) 称为图 G 的代数连通度（algebraic connectivity），其对应的特征向量称为Fiedler 向量。图G 的最大特征值λn(G) 称为图G 的谱半径（Spectral radius）。图G 是连通的，当且仅当其代数连通度大于0，即λ2(G) > 0。

2 一阶多智能体系统的一致性协议及其收敛速度

当通信拓扑为无向图时，在连续、周期采样和事件触发模式的一致性协议下，通信拓扑的代数连通度越大，收敛速率越高。并且，对周期采样和事件触发模式的一致性协议，为了让系统的通信负荷更小，还需要通信拓扑的谱半径越小越好。

2.1 连续模式的一致性协议及其收敛速率

假设多智能体系统有n个智能体，智能体i的状态ξi(t)表示一组表征智能体特征、随时间变化的物理量，如温度、位置、速度、加速度等。例如，如果智能体为平面上移动的质点，二维坐标位置表示其状态，状态向量记为ξi(t) =[xi(t)，yi(t)]T；如果智能体为在平面上的运动的无人车，二维坐标位置和速度表示其状态，此时ξi(t) =[xi(t)，yi(t)，vxi(t)，vyi(t)]T为其状态向量。

假设每个智能体的动力学为一阶积分器ξi(t) =ui(t)，其中ui(t)为控制输入。在通用的一致性协议［12-13］下，顶点i的控制量为

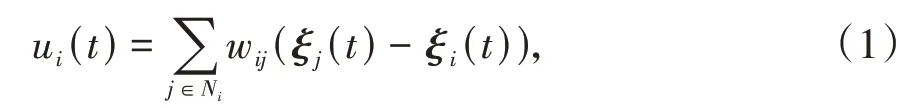
其中，Ni为智能体i的邻居集合。在一致性协议（1）作用下，如果对任意的i，j = 1，2，…，n 都有则称多智能体系统达到一致。

定理1［12，13］对一阶多智能体系统，如果通信拓扑G 为无向图，那么在一致性协议（1）作用下，系统能够达到一致当且仅当通信拓扑为连通图。一致性协议的收敛速度为e-λ2，其中λ2为通信拓扑的代数连通度。

由定理1，当一阶多智能体系统的通信拓扑为无向图时，代数连通度越大，一致性协议（1）的收敛速率越高。

2.2 周期采样模式的一致性协议及其收敛速率

周期采样模式下，每间隔固定时间h（也称为采用周期），多智能体系统中的智能体间进行一次信息交互，并更新控制输入。

由XIE等［19］设计的周期采样一致性协议如下

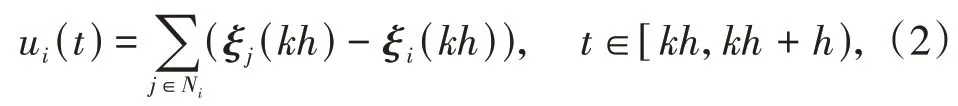
其中，ui(t)为智能体i 在时刻t 的控制输入，h > 0 为采样周期，为采样次数。由一致性协议（2），控制输入ui(t)为分段函数，在2 次采样间隔的时间内，保持不变。

定理2［19］对一阶多智能体系统，如果通信拓扑G为无向图，那么在周期采样一致性协议（2）作用下，系统能够达到一致当且仅当通信拓扑为连通图，且采样周期满足条件0 < h < 2/λn(G)。一致性协议（2）具有指数收敛速率，指数系数由通信拓扑的代数连通度λ2决定。

由定理2，一阶多智能体系统的通信拓扑为无向图时，谱半径越小，可选择更长的采样周期，收敛过程的通信负荷更小。并且，通信拓扑的代数连通度越大，一阶一致性协议（2）的收敛速率越高。

周期采样的一致性协议，解决了连续一致性协议模式下智能体硬件无法支持的缺陷。研究发现，周期采样模式下，尤其是采样周期的值较小时，依然存在大量无效通信［20］。

2.3 事件触发模式的一致性协议及其收敛速率

为解决周期采样模式下存在大量无效通信的问题，学者们开发了事件触发模式的一致性协议［21］。在事件触发模式下，智能体间只在需要的时候进行通信，极大地减少了冗余通信和冗余计算。

事件触发模式下，智能体上都设计有事件触发函数，当函数满足预设的条件时，智能体会与其邻居智能体进行通信。为了描述其工作原理，下面介绍DIMAROGONAS 等［22］设计的集中式事件触发一致性协议。

假设t0，t1，…为事件触发时刻，在一致性协议下，智能体i在时刻t的控制输入为

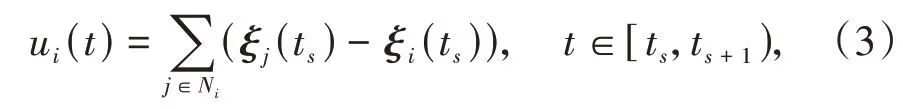
其中，Ni为智能体i 的邻居集合。由一致性协议（3），控制输入ui(t)为分段函数，在两次事件触发的时间间隔内，保持不变。

为确定事件触发时间，定义时刻t ∈[ts，ts+1)的误差向量err(t) = ξ(ts)- ξ(t)，其中向量ξ(t) =(ξ1(t)，…，ξn(t))T为系统的状态向量。无向图拓扑的一阶系统在一致性协议作用下，任意时刻系统状态的平均值是常数一致性协议（3）的事件触发条件为

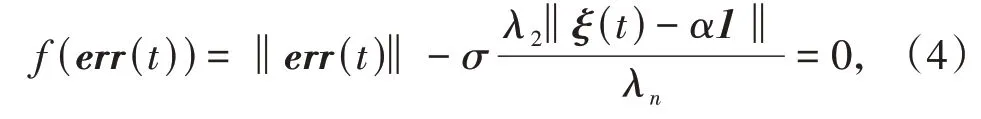
其中，参数0 < σ < 1，λ2和λn分别为通信拓扑的谱半径。

定理3［21，22］对一阶多智能体系统，如果通信拓扑为无向图，一致性协议（3）的事件触发条件为（4），系统能够达到一致当且仅当通信拓扑为连通图。一致性协议（3）具有指数收敛速率e2(σ-1)λ2，并且事件触发的最小时间间隔下界为τ =其中λ2和λn分别为通信拓扑的代数连通度和谱半径。

由定理3，通信拓扑的谱半径越小，事件触发的时间间隔会越大，收敛过程的通信负荷更小。并且，通信拓扑的代数连通度越大，事件触发一致性协议（3）在触发条件（4）下的收敛速率越高。

3 一致性收敛速率的拓扑优化方法

一阶多智能体系统的通信拓扑代数连通度越大，一致性协议收敛速率越高。因此，大量学者对代数连通度的最大化问题进行了研究。代数连通度是量化图连通性的重要参数［25］，在复杂网络［10，26］、多智能体系统［12］、传感器网络［27］、交通网络［28］、数字网络［5］和脑科学［29］等研究领域都有重要应用。例如，在复杂网络中，代数连通度是体现网络鲁棒性、可靠性和同步能力的参数。在这些学科的研究中，通常要求网络的代数连通度越大越好。下面针对提高一阶多智能体系统收敛速率的研究，总结当前采用的方法，重点介绍调整边连接方式提高收敛速率的方法。

代数连通度的最大化问题是指如何寻找一个满足给定约束条件的拓扑，使其具有最大的代数连通度。MOSK-AOYAMA 证明了代数连通度增广问题为NP-难问题［23］，此问题定义为：对给定的无向图G、非负整数k 和阈值r，能否给G 增加最多k 条边，使得加边后图的代数连通度不小于阈值r。因此，当图的顶点数和边数给定时，寻找代数连通度最大的拓扑结构也是NP-难问题。

实际应用中，受限于智能体通信链路数、通信半径和通信带宽等限制，以及通信网络的连通性和抗毁性等指标要求，代数连通度的最大化问题会附加更多的约束条件和目标要求。通常，这些限制和要求可以用图中的连边约束和参数表示，如通信链路数对应于顶点的度限制、通信半径可对应表示为顶点的连边限制、连通性可对应于图的点连通度或边连通度。与仅有顶点数和边数要求的代数连通度最大化问题相比，在这些限制和需求下寻找代数连通度最大的拓扑结构更加困难。

3.1 特殊图类的代数连通度

为刻画代数连通度与图结构的关系，学者们研究了一些特殊图类上的代数连通度上下界及其对应的极图。

对边数较少的连通图，由于拓扑结构相对简单，如树［30］、单圈图［31-32］和双圈图［33-34］，代数连通度的上下界及其极图都有明确的刻画。在给定顶点数的树图中，星图的代数连通度最大、路图的代数连通度最小。对特殊的树图，如毛毛虫图［35-36］、平衡二叉树［37］、直径相同的树［38］，代数连通度的上下界和极图也有一些比较明确的结论。单圈图的边数和顶点数相等，文献［31］中研究了单圈图的代数连通度，并对可能的拓扑进行了排序。如果单圈图的圈长已知，那么代数连通度最大的拓扑只有悬挂边［39］，代数连通度最小的拓扑为棒棒糖图［40］。

当图的边数较多时，其拓扑结构比较复杂，无法给出代数连通度最大或最小的拓扑结构，甚至无法给出代数连通度的上下界。目前，对代数连通度的上下界研究较多，主要研究的特殊图类有二部图、超立方体图、哈密尔顿图［23，25，41-42］以及给定特点参数特征的图，如给定直径、围长、周长、团数、独立数、匹配数和控制数等［43-48］。通过结构分析和大量实验，认为边比在顶点之间分布较均匀，并且直径比较小的图，可能具有较大的代数连通度。

3.2 代数连通度最大化问题的数学规划方法

为获得代数连通度最大的通信拓扑，一些学者将该问题建模为优化问题，利用优化算法进行求解。给定一个图G =(V0，E0)和可增加的边数k，代数连通度的增广问题描述为如下的模型

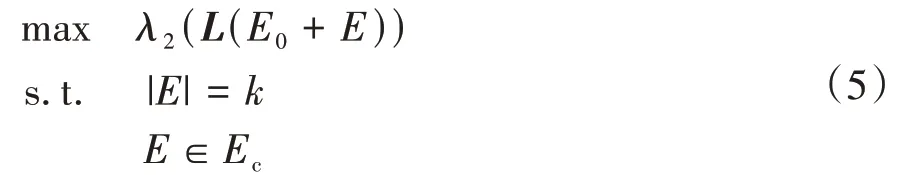
式中，Ec为图G 补图的边集。这里只有新增的边数限制，根据实际使用，可能还有每个顶点的度限制di≤Δi、边的最大权值限制wij≤ωˉ和点连通度限制等。

问题（5）并不是一个严格凸的规划问题，并且被证明为NP-难问题［39］。问题（5）转化为变量维数为|Ec|的0-1 整数规划问题，再把变量松弛为连续类型的半正定规划问题（SDP），进而求解代数连通度的上界［49-50］。通常，在SDP问题得到初始解之后，需要设计算法寻找满足整数条件的可行解，在可行解上寻找近似最优解。在点连通度大于κ 的约束下，文献［51］使用分枝定界法；在给定最大直径限制下，文献［52］使用割平面法和二分法，这些算法都得到了代数连通度较大的拓扑结构。基于松弛后的SDP 问题，有些学者设计了启发式算法求解可行解，进而得到较优的拓扑。文献［53］中，作者设计了3 种计算SDP 问题可行解的方法，提高了航空运输网络的代数连通度。文献［54］中，作者提出了2 种贪婪式启发算法求解SDP 问题，对代数连通度进行了优化，改进了异构光卫星网络的代数连通度。文献［5］中，为提高数字物流网络的代数连通度，作者提出了基于预算约束的最大-最小整数规划模型，并提出了贪婪算法、禁忌搜索算法你和带舍入的SDP算法进行求解。

值得注意的是，一个分布式的多智能体系统，通常无法在一个计算单元获取其全部的通信拓扑，设计分布式算法对代数连通度进行计算、估计和优化显得尤为重要。学者们利用多智能体系统分布式估计和求解分布式优化问题的能力，设计了估计系统自身拓扑网络代数连通度的分布式估计算法，目前已有相当多的结果［55-57］。最近也出现了使用分布式优化思想对代数连通度进行优化的文献［58-59］。

3.3 结构或权值调整的代数连通度优化方法

针对给定的无向图，在约束（如顶点的度）条件限制下，可采用调整连边方式或调整边权值的方法，使代数连通度增加。图的连边方式调整通常采用的方法有加边、边重连（删边再加边）、边旋转、边交换等操作。用这些操作可构造贪婪算法，迭代进行结构优化，进而提高代数连通度。因此，这些操作优化之后得到的图，无法保证是最优的结构。

3.3.1 增加边的方法

对给定的无向图，添加k条边，使得加边之后得到的图具有最大的代数连通度。文献［49］指出，通过向给定图添加边来最大化代数连通度是一个困难的组合问题。当增加的边数k 较大时，求最优解是异常困难的。因此，学者们研究添加一条边，使代数连通度增加最大的方法，进而设计贪婪算法，使得添加k 条边后，得到的拓扑具有较大的代数连通度［53，60-61］。

给无向图增加一条边，所有的特征值都不会减小，拓扑变化前后的特征值满足如下的交错引理。

引理1［32］假设G 是n 个顶点的无向图，vi和vj是图G 的两个顶点，且vivj∉E(G)。令G′= G +vivj，则有λ1(G) ≤λ1(G′)≤λ2(G) ≤λ2(G′)≤…≤λn(G) ≤λn(G′)。

由上述引理可知，当图G 的代数连通度重数大于等于2时，新增一条边，其代数连通度依然保持不变。然而，当图G 的代数连通度重数大于等于2时，删除一条边，代数连通度可能会减小。

利用交错引理，以及特征多项式在相邻两个特征值区间的单调性，用二分法可以快速计算加一条边之后的代数连通度。基于此理论，KIM 设计了加多条边的迭代算法［62］，在每一步迭代中选择使代数连通度增加最多的边。

图的特征向量也可用于预测增加边之后图的特征值变化情况。根据图的特征值和特征向量，分析和预测图结构发生变化之后的特征值是非常有意义工作。如下定理给出了增加或删除一条边之后特征值保持不变的场景。

定理4［63］假设G 是无向图，vi和vj是图G 的两个顶点。令λk为图G 的特征值，uk为其对应的特征向量。当vivj∉E(G)时，如果uk(i) = uk(j)，那么λk也是图G + vivj的特征值；当vivj∈E(G) 时，如果uk(i) = uk(j)，那么λk也是图G - vivj的特征值。

基于Fiedler向量的加边方法需要计算图的特征向量，当顶点数目较多时，准确地计算特征向量的是比较困难的。因此，有些学者研究了其他的加边策略，如以最小度顶点为端点，随机选择一个顶点添加一条边［60］或选择与之距离最远的顶点添加边［67］。这些连边策略能够对代数连通度进行较大的改进，并且具有较小的计算量，适用于规模较大的网络。

3.3.2 边旋转操作的方法

设G是一个赋权图，uv1∈E(G)且v2是图G中不同于的u和v1顶点。将边uv1从顶点v1旋转到v2的操作定义为：如果uv2∈E(G)，那么设置wuv2= wuv1+ wuv2，再删除边uv1；否则，在G 中增加边uv2，设置wuv2=wuv1，再删除边uv1。将边uv1从顶点v1旋转到v2得到的图记作G′= rotate(G，uv1，uv2)。

由定义可知，边的旋转操作有两类。如图1 所示，v1v5是图Ga的一条边，将边v1v5的顶点v5旋转到v2，得到图Gb= rotate(Ga，v1v5，v1v2)，此时图中减少一条边；将边v1v5的顶点v5旋转到v4，得到图Gc=rotate(Ga，v1v5，v1v4)，此时图中边数保持不变。

图在边的旋转操作之后，虽然某些顶点的赋权度发生变化，但所有顶点赋权度的和保持不变。在非赋权图中，指定的边不能旋转到已经存在的边上，即不能出现重边。

如下定理推广了非赋权图上边旋转操作的结论［68］，给出了边旋转操作使代数连通度减小的充分条件。

定理5 设G 是一个赋权无向图，uv1∈E(G)且v2是图G 中不同于的u 和v1顶点。图G′=rotate(G，uv1，uv2)为将G 中边uv1从顶点v1旋转到v2得到的图。假设u2是图G 代数连通度λ2(G)对应的一个特征向量。如果|u2(u) - u2(v1)| ≥|u2(u) -u2(v2)|成立，那么λ2(G′)≤λ2(G)。并且，如果条件的不等式是严格的，那么λ2(G′)< λ2(G)。

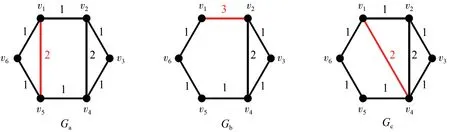
图1 赋权图中一条边的两类边旋转操作

为了通过边旋转操作，改变连边方式或改变边的权值，进而提高代数连通度，由定理5 得到如下推论。

推论1 设G 是一个赋权无向图，uv1∈E(G)且v2是图G 中不同于的u 和v1顶点。图G′=rotate(G，uv1，uv2)为将G 中边uv1从顶点v1旋转到v2得到的图。如果λ2(G′)> λ2(G)，那么对λ2(G)的任一特征向量uk都有|u2(u) - u2(v1)| < |u2(u) -u2(v2)|成立。

由推论1，基于λ2(G)的特征向量可选择合适的边旋转操作，使得代数连通度增加。

3.3.3 边交换操作的方法

设G是一个赋权无向图，u1v1和u2v2图G中两条没有公共端点的边。假设u1v2和u2v2都不是图G 的边，则u1v1和u2v2的边交换操作定义［69］：删除边u1v1和u2v2，如果图中存在边u1u2或v1v2，那么设置权值wu1u2= wu1u2+ wu1v1或wv1v2= wv1v2+ wu2v2；否则，新增边u1u2和边v2v1，设置权值wu1u2= wu1v1或wv1v2= wu2v2。如果新增加边为u1u2和v2v1，边交换之后得到的图记作G′= swap(G，u1v1，u2v2)；如果新增加边为u1v2和 u2v1，边交换之后得到的图记作 G′=swap(G，u1v1，v2u2)。

由边交换的定义可知，边交换操作连边方式的不同，边交换操作后得到两个不同的图。为了区别这两个图，符号中的两个边的顶点默认是有顺序的，新连接边的方式按照两条边中顶点出现的顺序一一对应。如图2 中，边v1v2和v2v4在交换时，可能出现两个组合。在图Gb= swap(Ga，v1v5，v2v4)中，删除这两条边后，顶点v1和v2为新增边对应的顶点，由于边v1v2已经存在，修改其权值即可；同样，顶点v5和v4为新增边对应的顶点，由于边v5v4已经存在，修改其权值即可。在图Gc= swap(Ga，v1v5，v4v2)中，新增边v1v4和v5v2，分别将边v1v5和v2v4的权值赋予新增边。

图2 赋权图中两条边的两类边旋转操作

文献［69］中，针对非赋权的无向图，给出了边旋转操作之后代数连通度减小的充分条件。作者在文中说明，此充分条件可直接推广到赋权图。如下定理给出了赋权图中，两条边在边交换操作后，代数连通度减小的充分条件。

定理6［69］设G 是一个无向图，u1v1和u2v2是图G 中两条没有公共端点的边。图G′=swap(G，u1v1，u2v2)为将u1v1和u2v2进行边交换操作得到的图。假设u2是图G 代数连通度λ2(G)对应的一个特征向量。如果(uk(u1)- uk(v2))(uk(v1)-uk(u2)) ≤0成立，那么λ2(G′)≤λ2(G)。

为了使用边交换操作，改变图的拓扑结构或边上的权重，进而提高代数连通度，必须选择合适的边进行边交换操作。由定理6得到如下推论。

推论2［69］设G 是一个无向图，u1v1和u2v2是图G 中两条没有公共端点的边。图G′= swap(G，u1v1，u2v2)为将u1v1和u2v2进行边交换操作得到的图。如果λ2(G′)> λ2(G)，那么对λ2(G)的任一特征向量uk都有|u2(u) - u2(v1)| < |u2(u) - u2(v2)| > 0成立。

本节提出的加边操作、边旋转和边交换操作可组合使用设计算法，能对图进一步优化，得到代数连通度更大的拓扑结构。

4 结语

通信拓扑为无向图的一阶多智能体系统，收敛速度由通信拓扑的代数连通度决定的，代数连通度越大，系统达到一致性的收敛速度越快。由于代数连通度最大化问题是NP-难问题，当系统规模较大时无法得到最大值和最优拓扑。目前对通信拓扑代数连通度的优化，主要采用的方法有数学规划方法和边或边权值调整方法。数学规划方法将代数连通度最大化问题建模为非凸的整数规划问题，松弛处理后，设计优化算法可得到较好的拓扑结构。但是这类优化问题算法复杂性高，网络规模较大时无法有效应用。边或边权值调整方法，通常先考虑一到两条边的最优调整方案，然后设计贪婪算法，每步迭代都能提高代数连通度。该方法计算量小，通常能得到较好的拓扑结构，但是无法保证得到的拓扑是最优的。

针对多智能体系统拓扑优化，目前依然有很多待改进和未解决的问题。首先，当前大部分的优化基于已知拓扑结构进行的。实际上由于多智能体系统的分布式特征，无法在一个计算单元获取所有的通信拓扑信息。因此，采用分布式估计和分布式优化方法对多智能体系统拓扑参数进行估计和优化是后续研究的趋势。其次，考虑新增若干个智能体接入到多智能体网络，如何设计最优的连边方式，使得系统的收敛速率最大？另外，如果某个智能体发生故障，如何进行拓扑重连使得收敛速率最大？这些系统中智能体个数发生变化的问题，由于问题的复杂性，目前很少有研究。最后，如果多智能体系统中存在有向边时，由于网络拓扑对应的拉普拉斯矩阵为非对称矩阵，特征值可能为复数，一阶多智能体系统的收敛速率由非零特征值的最小实部决定。因此，当多智能体系统的通信拓扑为有向图时，收敛速度的优化将更加有挑战性。