基于惠斯通电桥的弯曲应变测量灵敏度研究

代国红，许艺铧，吴庆丰，沈 云，韩道福，邓晓华,c

(南昌大学a.物理与材料学院;b.高等研究院;c.空间科学与技术研究院，江西 南昌 330031)

利用惠斯通电桥测中值电阻是经典的电学实验之一，其测量原理是通过等电势法测电阻，具有操作简单、测量精度高等特点[1]，这种电路连接方式最早是由英国人惠斯通在用比较法进行电学测量时发明，故此得名[2]。它将待测电阻和标准电阻相比较，以确定待测电阻和标准电阻之间倍率关系，从而实现电阻的精确测量。这种可测电阻范围为几十到几十万欧姆[3]，它不仅可以测量一些电学量诸如电阻、电容、电感等，而且配合不同的传感器，还可以测量很多非电学量[4]，如温度、压力、湿度、位移等。例如电阻式传感器，便是通过电阻参数的变化来实现电学方法测量非电学量的目的。因此，惠斯通电桥结合电阻式传感器在自动检测和自动控制领域得到了广泛的应用。而在实际工程应用过程中，例如铁路桥梁的应力检测，温度的变化等，此时桥臂电阻往往是具有一定功能的传感元件，电桥测量的灵敏度对于动态检测至关重要[5]，最新的研究表明惠斯通电路在磁阻传感器方面也有很好的应用前景[6]。此外，考虑到惠斯通电桥在实际使用过程中，桥路输出电压与电阻相对变化率存在非线性关系，通过改进实验装置消除非线性关系带来的影响显得尤为重要。

1 电桥电压灵敏度与桥臂电阻比例关系的理论分析

灵敏度是电桥测量技术的一个重要指标，电桥电压灵敏度与很多因素有关，如选择更高的供电电压时，其灵敏度会增加。电桥的灵敏度可以用电桥测量臂电阻的单位相对变化量引起输出端电压或电流的变化来表示[7]。电桥的电压灵敏度和电流灵敏度分别表示为：Su=ΔU/(ΔR/R)和Si=ΔI/(ΔR/R)。在本文中，我们采用的是桥路电压与电源电压的相对变化率，从而避免电源电动势选取的不同而带来不同的电压灵敏度。

直流电桥的电压灵敏度定义为[8]：

(1)

其中E为电源电动势，当某一桥臂电阻由R变为R+ΔR时，桥路电压由U变为U+ΔU。

电路图如图1所示，桥路上的电压U可写为：

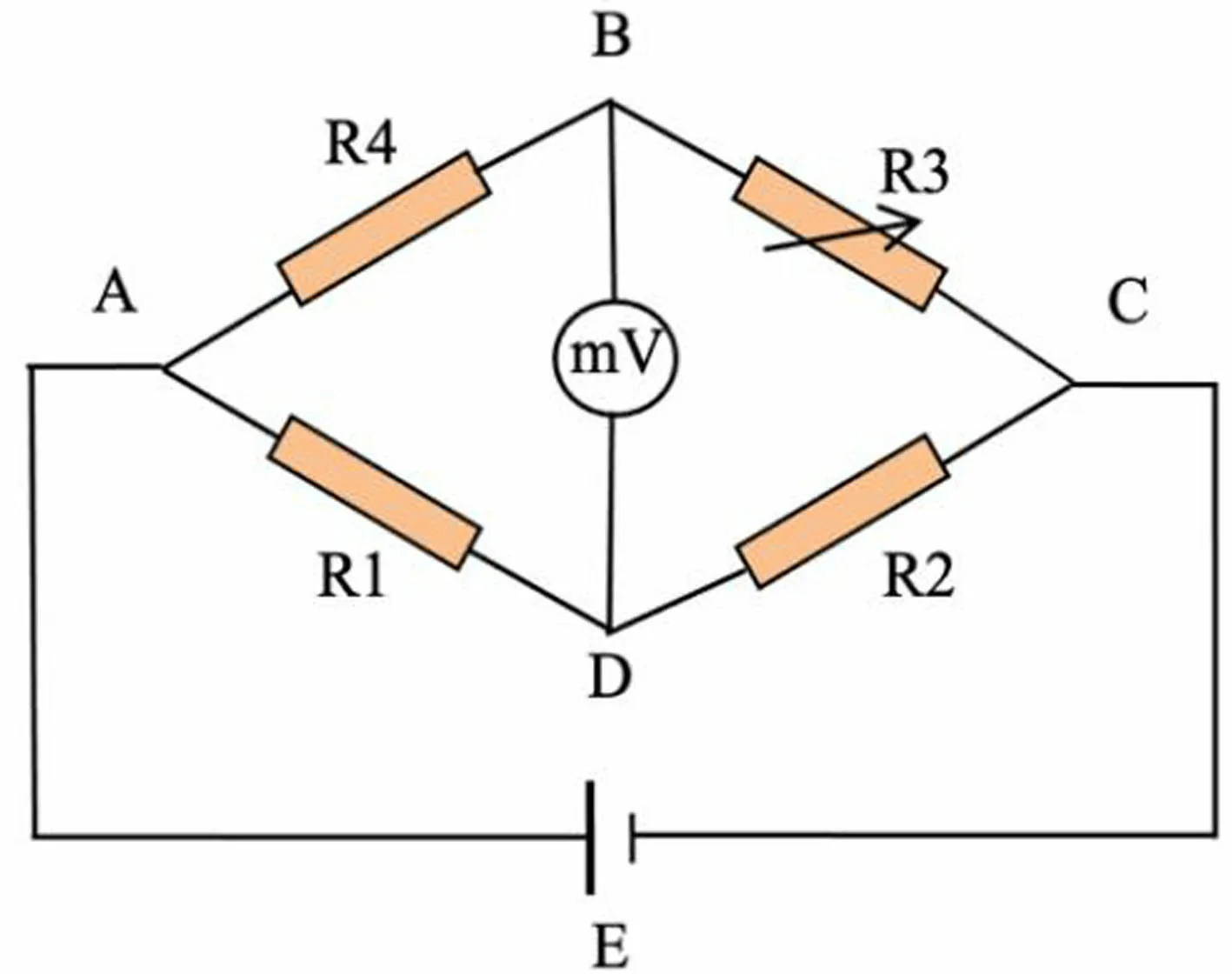
图1 惠斯通电桥电路图

(2)

(3)

(4)

(5)

考虑到ΔR3≪R3，因此(5)式可写为

(6)

(7)

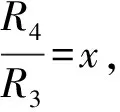
(8)

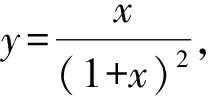
x

2 电桥电压灵敏度与桥臂电阻比例关系的实验研究

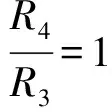
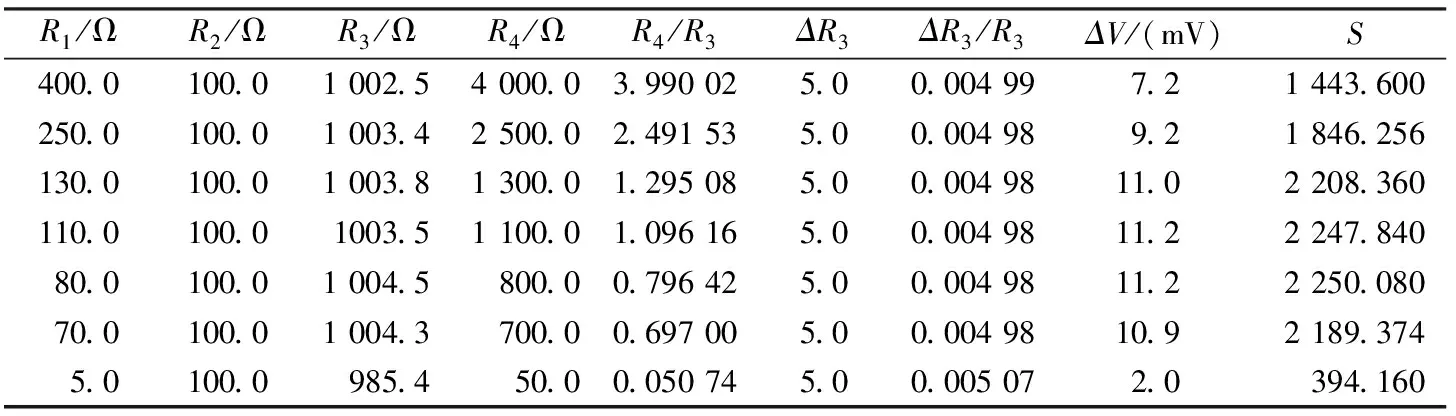
表1 电压灵敏度与R4和R3比值的关系表格

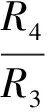
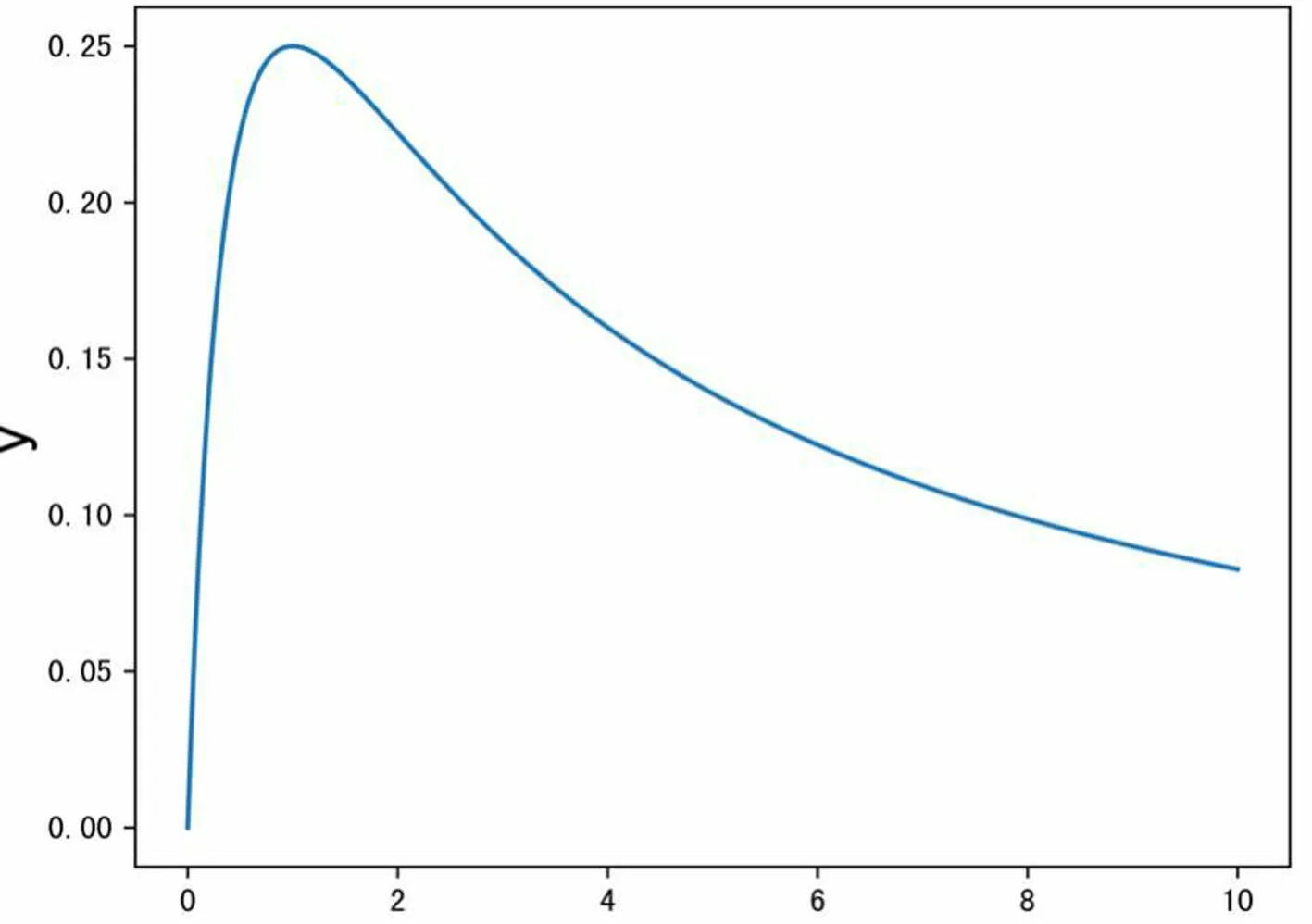
R4/R3

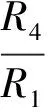
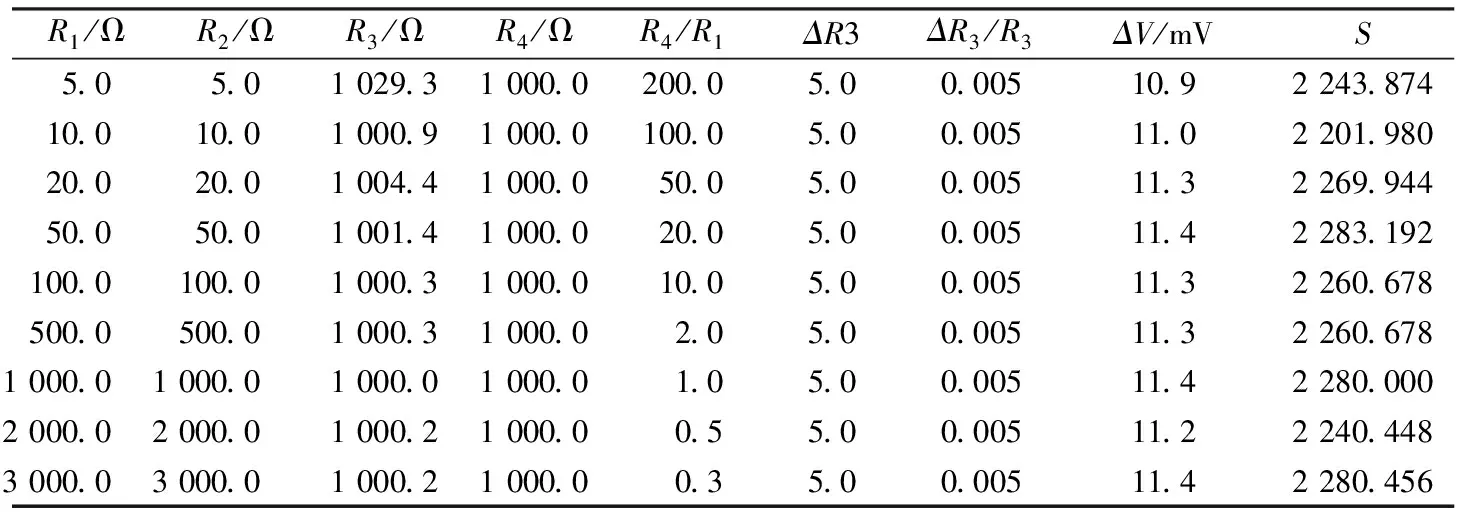
表2 电压灵敏度与R4和R1比值的关系表格

当R4与R3的比值为1时，此时无论R4与R1的比值如何改变，电桥的灵敏度都不再改变，这一研究结论也与相关文献[11]报道一致。电压灵敏度S与桥臂电阻比值R4/R1之间的关系曲线如图4所示。

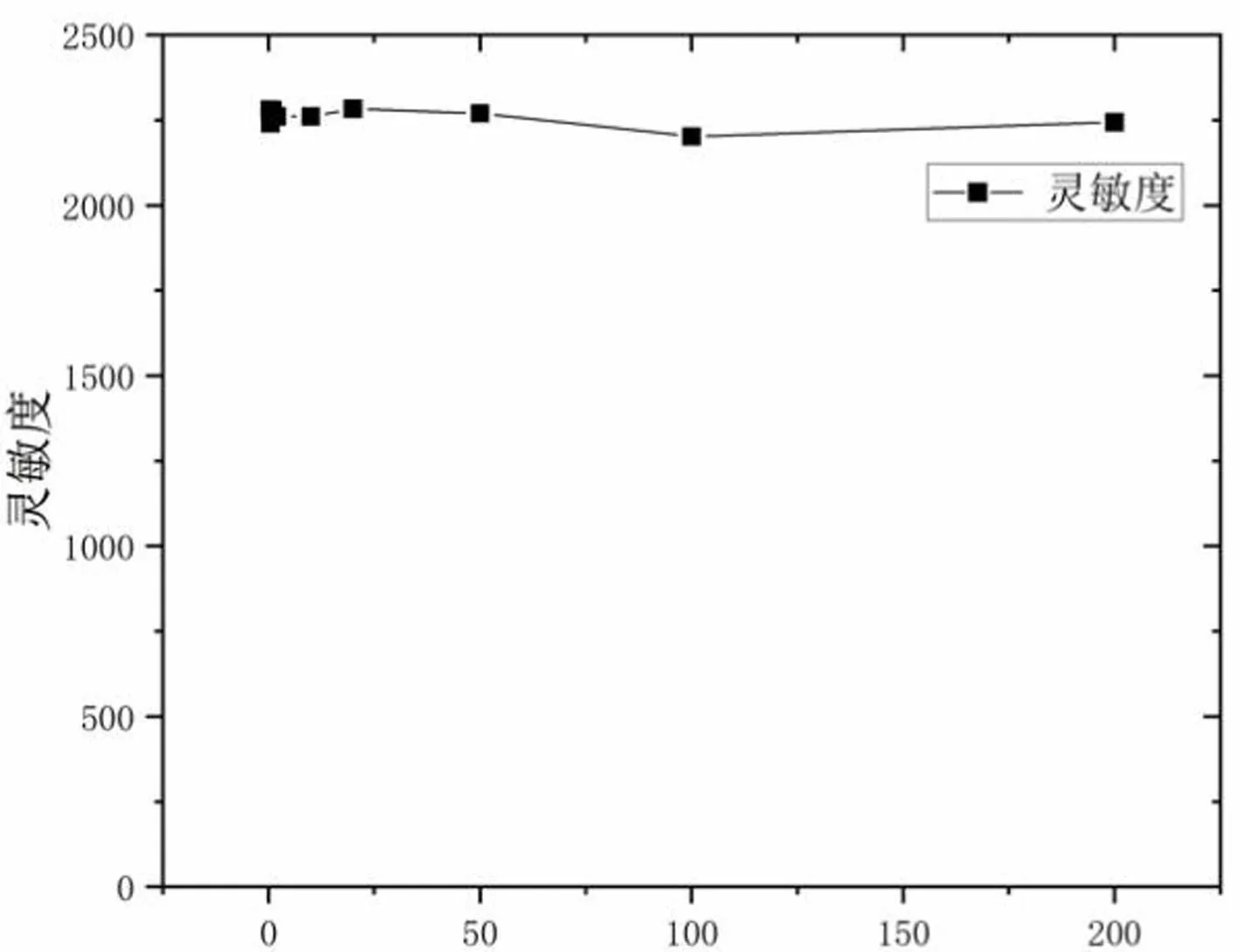
R4/R3

3 惠斯通电桥非线性的消除

半桥差动电路如图5(a)所示，我们注意到

ΔU=UB-UD=

(9)

当满足ΔR3=ΔR4，R3=R4，R1=R2时，代入(1)式得

(10)

由(9)式、(10)式可知，桥路输出电压与电阻相对变化为线性关系，半桥差动电路可以消除非线性效应对电桥的影响。电阻应变片可用于测量应变的元件，当导体或半导体材料在外界力的作用下产生机械变形时，其电阻值将会发生相应的变化。

为满足ΔR3=ΔR4，R3=R4，R1=R2：如图5(b)所示，我们在材料表面粘贴电阻应变片，以实现ΔR3=ΔR4，R3=R4。我们将滑动变阻器的滑片置于变阻器线圈中间位置，使R1=R2。为保证应变片变化明显，且便于观察，将其粘贴在待测试的塑料卡片上，组装半桥差动电路，使电桥处于平衡状态。改进后的电路如图5(c)所示。

(a)半桥差动电路图

在应变片处于不受力状态下，测量其长度L0及其厚度d，当应变片受力时将会发生弯曲，如图6所示。

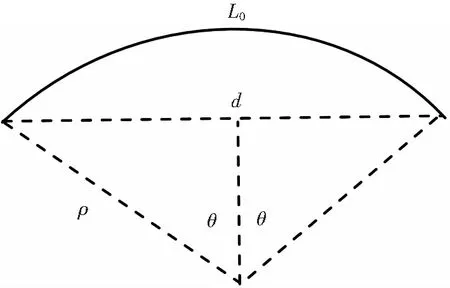
图6 弯曲应变的塑料片示意图

由几何分析可得

(11)

(12)

联立(11)、(12)可得

(13)

由式(13)可知，我们只需在实验前测量塑料卡片的长度和厚度，实验时测量塑料卡片应变状态下圆弧的弦长，即可计算出对应的应变[12]。

我们选用长为85.70 mm、厚为0.80 mm的测量卡片进行实验，首先将塑料卡片弯曲在游标卡尺之间，测量弯曲圆弧的弦长L0。

在不同应变状态下，分别测量电压，结果如表三所示。

图7 弯曲应变过程中弦长的测量图

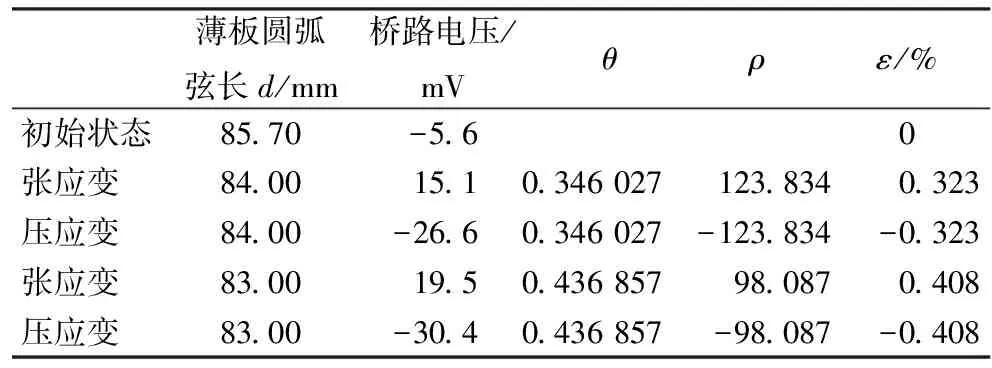
表3 应变状态下的桥路电压输出结果

对测得的实验数据进行线性拟合，如图8所示，拟合后得到桥路电压随应变的变化关系为：

应变/%

ΔU=62.5ε-5.6

(14)

式中ΔU为半桥差动电路桥路输出电压，ε为弯曲应变。由图8可知，半桥差动电路桥路输出电压与应变片的弯曲应变之间呈线性关系变化。

4 结论