载荷敏度抑制下涡轮盘拓扑优化及结构演化

闫浩，吴晓明

厦门大学 航空航天学院，厦门 361102

航空航天飞行器结构承受惯性载荷，发动机涡轮工作时要承受极大的离心力，大型土木建筑中结构自重是不可忽略的重要载荷。自重和惯性力这类载荷的特点是结构与载荷相互耦合，结构的变化会引起载荷大小的变化，呈现“没有结构则没有载荷”的特征，称为设计相关载荷。

针对设计相关载荷的结构拓扑优化方法得到了国内外学者的广泛关注。Bruyneel和Duysinx采用基于梯度的移动渐近线法(Gradient-Based Method of Moving Asymptotes, GBMMA)求解，讨论了固定载荷与自重的比例对拓扑结构的影响。高彤等采取对角二次逼近法(Method of Diagonal Quadratic Approximations，MDQA)进行优化求解，提出了一种可变参数的材料属性有理近似模型(Rational Approximation of Material Properties，RAMP)，避免固体各向同性惩罚模型(Solid Isotropic Material with Penalization, SIMP)处理惯性载荷问题存在的“附属效应”。张晖等研究了自重载荷作用下的连续体结构的拓扑优化问题，使用了移动渐近线(Method of Moving Asymptotes，MMA)方法求解，提出了RAMP材料插值模型和平均敏度过滤技术相结合的求解策略，以克服柔度随单元密度变化的非单调行为。Yang等对渐进结构优化(Evolutionary Structural Optimization,ESO)和双向渐进结构优化(Bi-directional Evolutionary Structural Optimization, BESO)拓扑优化方法中的固定载荷条件下的灵敏度分析和进化过程进行了改进，以适应设计相关载荷状况。Huang和Xie提出了一种基于灵敏度数计算的BESO方法，算例验证了该方法对含自重载荷结构拓扑优化的有效性。Lee和Martins对设计相关的压力载荷作用下的拓扑优化问题，运用材料边界识别方法进行载荷施加，并提出了一种求解载荷敏度的解析方法。易垒和文毅针对目标函数对设计变量的非单调性，提出在优化准则法的迭代式中对惯性载荷敏度进行修正。

自专利文献[8]提出一种新型双辐板涡轮盘以来，国内外众多学者开展了针对航空发动机涡轮盘在设计相关载荷下的拓扑优化研究。董少静等采用渐进结构优化算法对涡轮盘进行拓扑优化，得到了双辐板涡轮盘的结构形式。张乘齐等先通过拓扑优化得到双辐板涡轮盘基础轮廓，再通过形状优化对双辐板涡轮盘形状进行设计。Rindi等运用水平集方法 (Level Set Method,LSM)法对某型涡轮盘进行了优化；Xu等将导重法(Guide Weight, GW)引入连续体结构在惯性力作用下的拓扑优化，对一些典型的设计相关载荷拓扑优化算例进行了计算，并且与前人的研究结果进行了对比。陆山和赵磊基于ANSYS软件，建立了双辐板涡轮盘优化设计平台，针对某高压涡轮转子，设计了2种双辐板涡轮盘。

基于变密度结构拓扑优化模型，应用优化准则法推导惯性载荷下的求解迭代格式，针对设计相关载荷SIMP模型的材料附属效应运用一种新的指数材料性能近似模型；提出一种新的密度过滤方法；针对设计相关载荷带来的目标函数非单调问题提出一种载荷敏度抑制方法。同时讨论了载荷敏度抑制因子与涡轮盘拓扑结构的关系。通过有限元建模，比较分析了所得到的单辐板和双辐板涡轮盘结构。

1 结构拓扑优化模型

以结构柔度最小化为优化目标的变密度法结构拓扑优化数学模型如下：

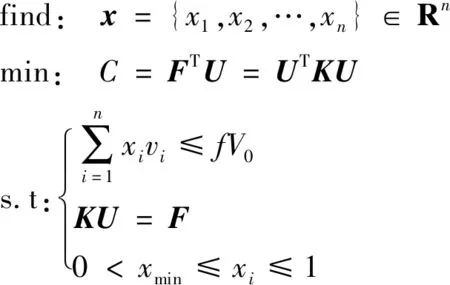
(1)

式中：为设计域内有限元单元的相对密度向量；为单元总数；为整体结构柔度值；、与分别为结构整体刚度矩阵、位移向量与载荷向量；为单元体积；、分别为设计区域初始体积与体积分数；为设计变量的下限。

模型式(1)中目标函数对设计变量的灵敏度和基于K-T条件的设计变量迭代格式分别如式(2) 和式(3)所示：

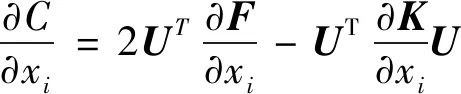
(2)

(3)

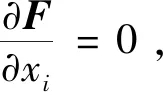
2 材料插值模型与灰度抑制方法

2.1 材料插值模型

若变密度拓扑优化方法中插值模型函数为()，则弹性模量、自重或离心载荷等设计相关载荷与单元相对密度之间的关系为

(4)

式中：为实体材料的弹性模量；0为实体材料第单元的惯性力。因此，载荷与弹性模量之间的比值如式(5)所示：

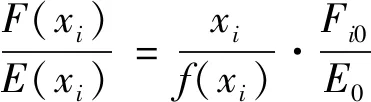
(5)

在SIMP插值模型中()=(>1)，为SIMP插值模型中的材料惩罚因子,由式(5)可知，在低密度单元中，设计相关载荷与弹性模量的比值会非常大，如图1所示。这种由于插值模型引起的弱材料单元无法承载自身惯性载荷现象，被称为“材料附属效应”。这种附属效应会导致计算无法进行或者使优化结果不稳定，也可能会使优化的拓扑结构存在不合理的分支结构。

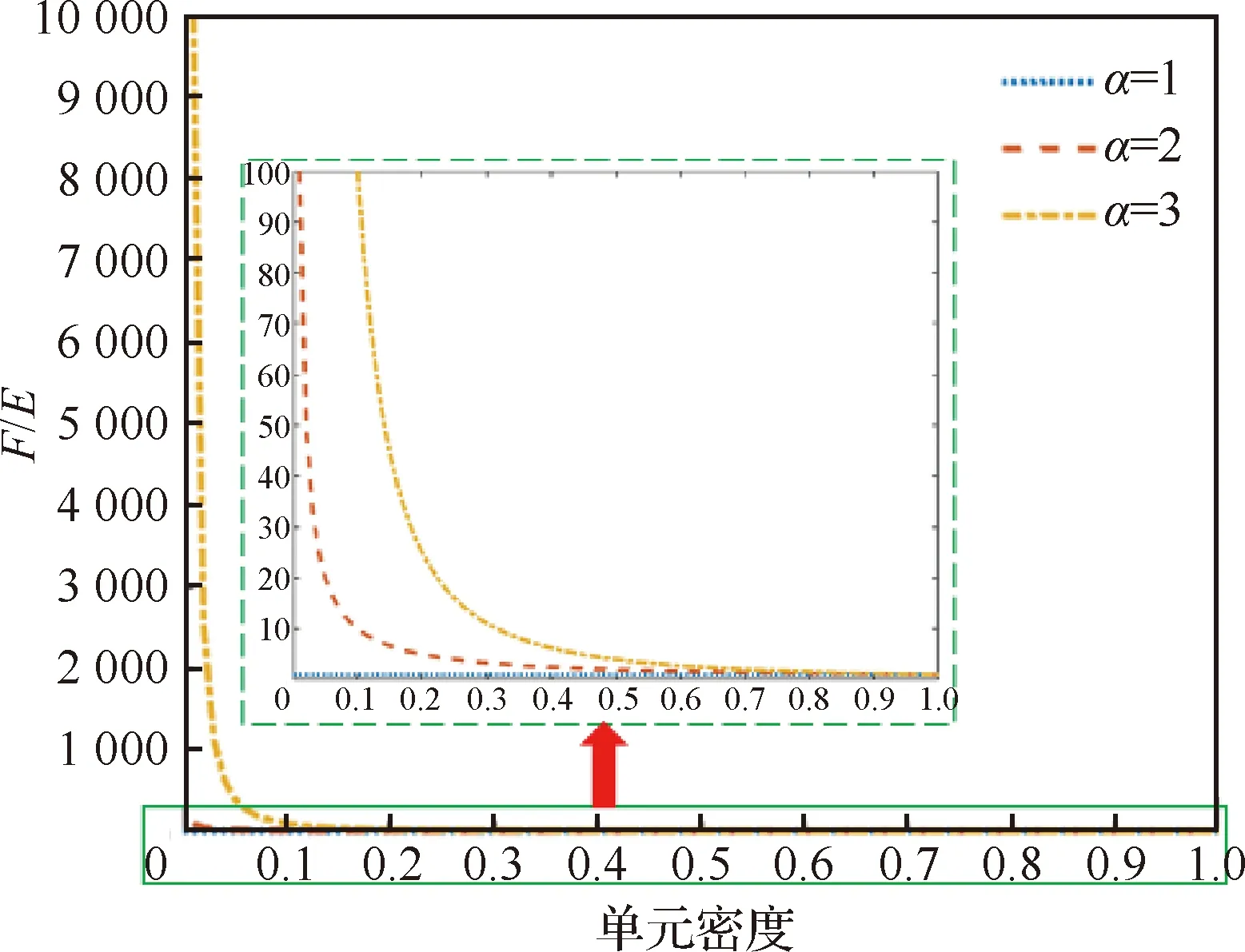
图1 SIMP模型下载荷与弹性模量比值Fig.1 Ratio of load to elastic modulus in SIMP model

为了克服这种材料附属效应，文献[1]应用了一种改进的分段SIMP插值模型方法，使得在低密度单元两者的比例不再趋于无限大。文献[2]采用RAMP模型，其材料插值函数如式(6)所示:

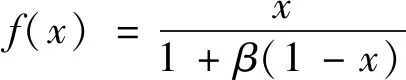
(6)

为RAMP插值模型中的材料惩罚因子,载荷与弹性模量的比值如式(7)所示：

(7)

由式(7)绘制RAMP模型对应的载荷与弹性模量之间的比值示意图，如图2所示。由图2可知在RAMP模型中，低密度单元上两者比值始终在有限值范围内。

图2 RAMP模型下载荷与弹性模量比值Fig.2 Ratio of load to elastic modulus in RAMP model

文献[15]提出了一种材料性能指数近似模型(Exponential Approximation of Material Properties，EAMP)，其材料插值函数如式(8)所示:

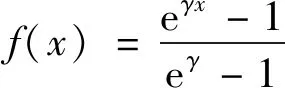
(8)

式中:为EAMP插值模型中的材料惩罚因子。对应的函数图像如图3所示。

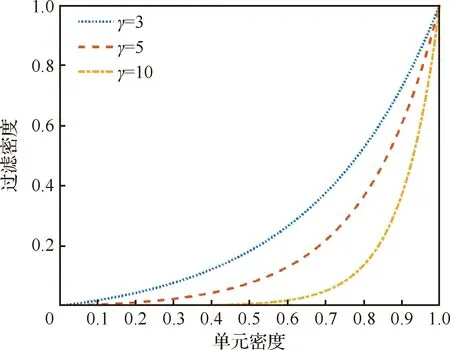
图3 EAMP材料插值模型函数Fig.3 EAMP material interpolation model function

其载荷与弹性模量的比值如式(9)所示:

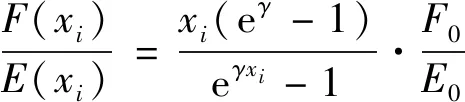
(9)

根据式(9)绘制EAMP模型对应的载荷与弹性模量之间的比值示意图，如图4所示。

由式(9)及图4可知，EAMP模型中，在低密度区间内，载荷与弹性模量的比值也始终保持在有限值范围内，同时算例表明EAMP材料插值模型能够有效提高优化迭代的收敛速度。

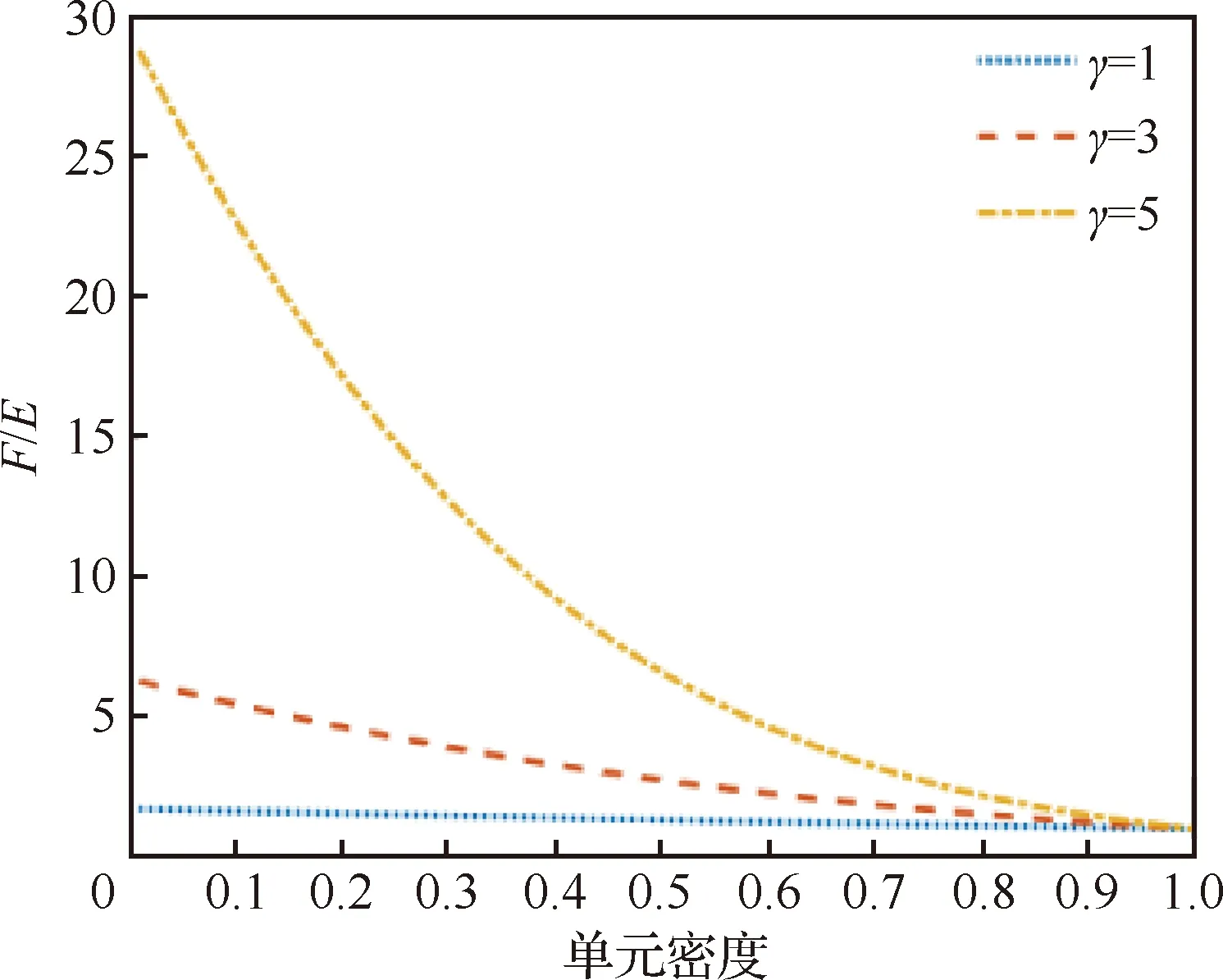
图4 EAMP模型下载荷与弹性模量比值Fig.4 Ratio of load to elastic modulus in EAMP model

2.2 新的灰度抑制方法

结构边界不清晰，灰度单元多是拓扑优化结果中普遍存在的问题，基于EAMP材料插值模型，提出了一种灰度抑制方法。基于此方法的新的迭代格式如式(10)所示：

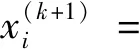
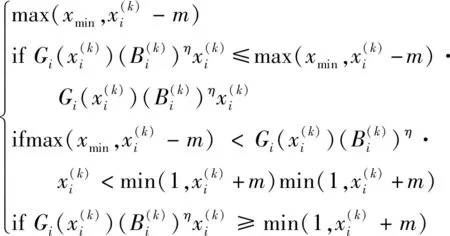
(10)

为了验证基于EAMP模型的灰度抑制方法的可行性，对经典悬臂梁结构分别进行不使用灰度抑制和使用EAMP灰度抑制进行拓扑优化。

如图5所示，设计域为长、宽0.5的矩形平板结构，将设计域离散为80×40个有限单元，结构左侧固定位移全约束，右侧受到向下的固定载荷。

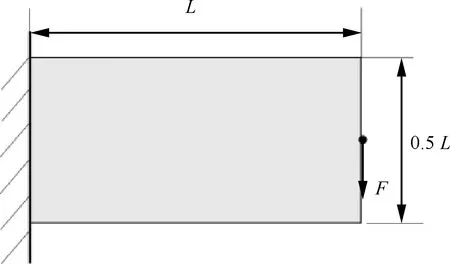
图5 悬臂梁结构示意图Fig.5 Schematic diagram of cantilever structure

为了比较度量拓扑优化结构中的单元灰度，运用文献[16]中的表征结构灰度值如式(11)所示，越小则结构的整体单元灰度越小。

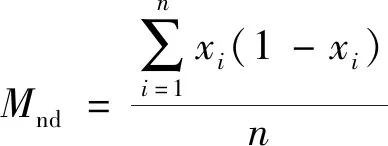
(11)

图6为不使用灰度抑制和使用EAMP灰度抑制方法得到的拓扑优化结构，各自的值、优化步数、目标函数如表1所示。

由图6可知，使用EAMP灰度抑制之后的拓扑结构明显更加清晰，单元灰度更小。由表1可知，在目标函数接近的情况下，使用EAMP灰度抑制方法比未进行灰度抑制的结构灰度值降低了84.5%，迭代收敛的步数也降低了70%。

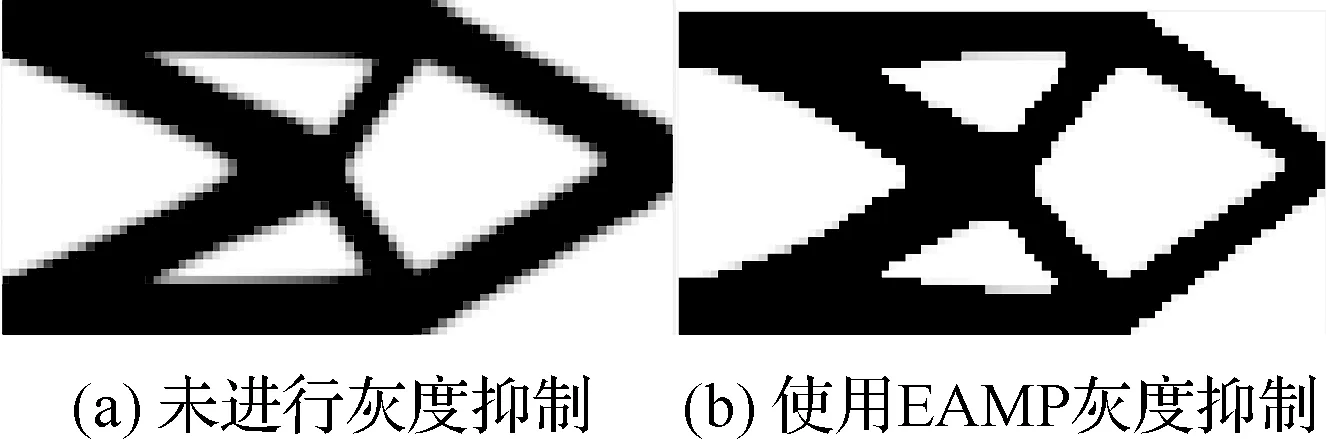
图6 优化结构图Fig.6 Optimization structure chart

表1 灰度抑制结果Table 1 Gray suppression results

算例表明基于EAMP材料插值模型的灰度抑制方法的有效性，此方法可以有效地减少拓扑结构中的灰度单元并且可以更快达到收敛。

3 载荷敏度抑制方法

由式(2)可知，当载荷为设计相关载荷时，目标函数对单元密度的敏度式不再恒为负，即目标函数不再单调。为此提出一种载荷敏度抑制算法，在式(2)载荷敏度项前添加一个抑制因子1/(+1)。添加抑制因子之后，目标函数对设计变量的灵敏度为

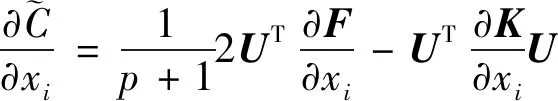
(12)

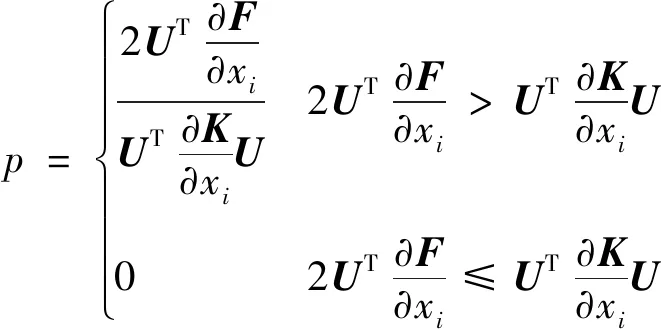
(13)

抑制因子作用于优化过程的每一次迭代中，其作用如图7所示，其中实线为刚度敏度，点划线为抑制前的载荷敏度，虚线为抑制后的载荷敏度。经过载荷敏度抑制使目标函数保持单调。

图7 载荷敏度及其抑制算法示意图(局部放大)Fig.7 Schematic diagram of load sensitivity and its suppression algorithm (Local amplification)

对于抑制后的敏度式(12)，采用Sigmund敏度过滤方法，得到迭代格式(10)中的迭代系数为

(14)

优化求解的流程图如图8所示。

图8 优化求解流程图Fig.8 Flow chart for optimization solution

为了验证此方法的有效性，对照文献[3，5，7]中的自重载荷算例，在相同计算条件下使用所提出的载荷敏度抑制算法进行计算，对拓扑优化结果进行比较。表2为文献中算例的计算参数设置。

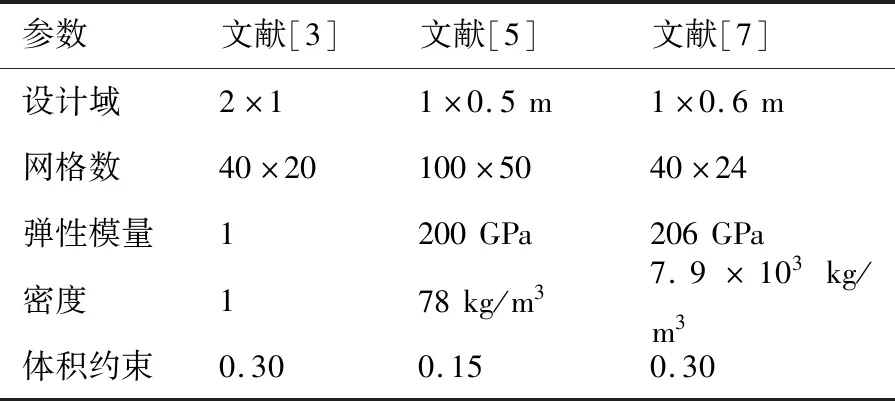
表2 文献算例参数Table 2 Reference example parameters

表3为文献与载荷敏度抑制算法所得到的拓扑结构。由表3可知，在计算参数相同的情况下，载荷敏度抑制算法与文献算例的结构相似。文献[5]给出了算例的目标函数值3.82和收敛步数80，本文载荷敏度抑制算法得到的目标函数值3.79，收敛迭代步数30，目标函数值略低且收敛速度更快，说明载荷敏度抑制算法在自重载荷拓扑优化中的有效性。

表3 不同算法得到的拓扑优化结构Table 3 Topology optimization structure obtained by different algorithms

4 发动机涡轮盘拓扑优化

航空发动机涡轮盘工作时要承受极大的离心载荷，是一种典型的设计相关载荷的结构优化问题。在美国 “综合高性能涡轮发动机技术”(Integrated High Performance Turbine Technology，IHPTET)计划的第3阶段中，验证了双辐板涡轮盘在结构传力路径等方面的优势，且其较单辐板涡轮盘质量减轻、转速提高。1999年Cairo申请了双辐板涡轮盘结构的专利，2001年Burge发明了应用于压气机的双辐板轮盘结构，2007年Harding和Curtiss发明一种盘毂尺寸较大的双辐板涡轮盘结构。

相关研究已经表明，在相同的载荷和设计边界条件下，双辐板涡轮盘较单辐板涡轮盘具有降低最大应力、变形小等优势。但是从拓扑优化算法角度，单辐板与双辐板结构之间如何演化，以及这样的演化受到哪些因素的影响未见文献报道。以下根据本文提出的载荷敏度抑制算法进行讨论。

4.1 抑制因子对涡轮盘拓扑结构的影响

抑制因子1/(+1)中的由式(13)定义，与单元的载荷敏度和刚度敏度相关，由式(12)和式(14) 可以看出，抑制因子的大小决定了载荷敏度在求解迭代格式(10)中的影响。有学者为避免设计相关载荷目标函数的非单调问题，在优化迭代计算时直接忽略载荷敏度项。为讨论载荷敏度对最终拓扑结构的影响，将式(12)中的抑制因子设置为1/(+)，称为抑制系数，当从小到大变化时，载荷敏度在迭代格式(10)中的影响逐步变小，讨论此时拓扑结构的演化。

将涡轮盘的径向截面设置为一个高宽为×2的矩形平面，离散为50×100个四边形有限单元。矩形平面绕左侧距离为的轴旋转，转速为，如图9所示。

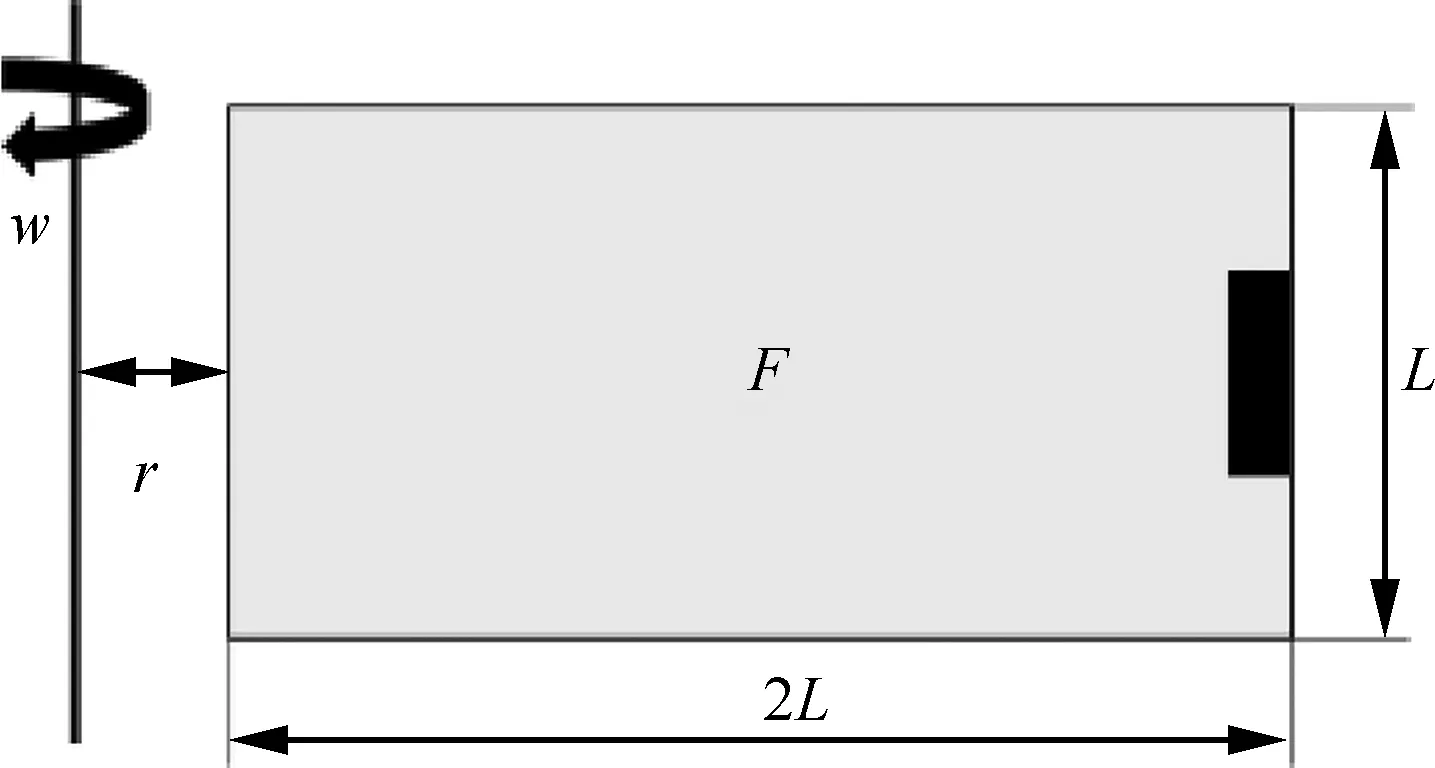
图9 结构示意图Fig.9 Structure diagram

运用本文所提出的算法，其中EAMP插值模型和灰度抑制的惩罚因子分别为、，敏度过滤半径为，体积分数为，计算参数的具体数值如表4所示。

表4 算例3参数Table 4 Parameter of Example 3

在抑制系数取0.1、1、10、100、1 000、10 000、100 000和无穷大(即不考虑迭代式中的载荷敏度项)的情况下，对应的涡轮盘拓扑结构演化规律如图10所示，其中横坐标为抑制系数的常用对数。

由图10可见，涡轮盘径向截面的拓扑结构随抑制系数的增大(载荷敏度在迭代式中的影响变小)，由双辐板结构逐渐演化为单辐板结构。抑制系数取1 000和10 000之间存在一个临界点，在此临界点附近拓扑结构从双辐板向单辐板突变。应用二分法计算的临界点为2 301和2 302，如图11所示。

图10 抑制系数变化时拓扑结构演化图Fig.10 Topological structure evolution diagram with variation of suppression coefficient

图11 临界点附近的拓扑结构演化图Fig.11 Topological structure evolution graph near critical point

当抑制系数取2 301时，结构为双辐板结构，取2 302时，结构为单辐板结构。为了进一步探究抑制系数对结构演化的作用，分别计算抑制系数取2 301和2 302时，优化迭代过程中拓扑结构的演变过程。

从图12可以看到，2个抑制系数下拓扑结构在迭代65步之前得到的结构是相似的，在65～72步之间结构发生不同演变，=2 301时结构的上下辐板得到加强，逐步演化为双辐板结构。=2 302时结构中间的辐板得到加强，逐步演化为单辐板结构。

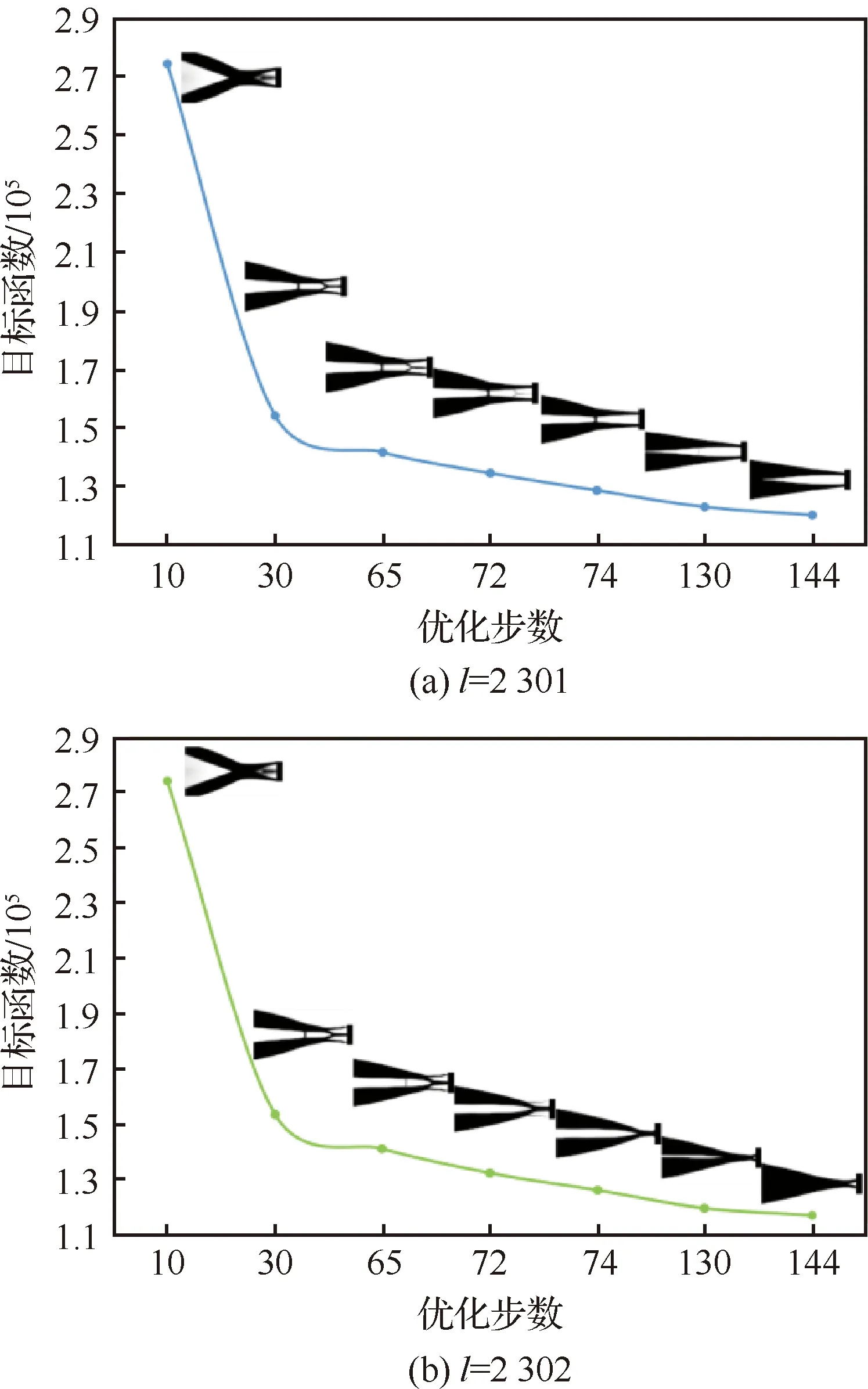
图12 迭代过程中拓扑结构的演变图Fig.12 Evolution graph of topological structure in iterative process

通过典型大惯性载荷算例3中抑制系数大小对拓扑结构演化的讨论可以看出，一方面设计相关载荷的载荷敏度对最终的拓扑优化结构有关键性作用。当抑制系数较小，即载荷敏度在迭代式中保留较大时，涡轮盘径向截面优化拓扑为双辐板结构。抑制系数较大，即载荷敏度在迭代式中保留较小时，拓扑结构为单辐板结构。另一方面，从图10可以看出，涡轮盘从双辐板结构向单幅板结构演化过程中，目标函数逐步增加，即结构柔度增大，刚度减小。但图11显示，在抑制系数的临界点附近，双辐板结构可能与单辐板结构刚度相当甚至更差。

将算例3得到的2种涡轮盘径向截面拓扑结构设计成涡轮盘模型进行有限元分析，对其强度和刚度进行比较分析。

4.2 几何建模与有限元分析

算例3中当取值非常小时涡轮盘的拓扑结构为典型的双辐板结构，当取值无穷大时涡轮盘的拓扑结构为单辐板结构，见图13。对2种拓扑结构分别建立涡轮盘的几何模型，如图14所示，对2个几何模型分别施加相同的约束条件，进行有限元分析，得到应力、应变能结果以及模型的质量如表5所示。

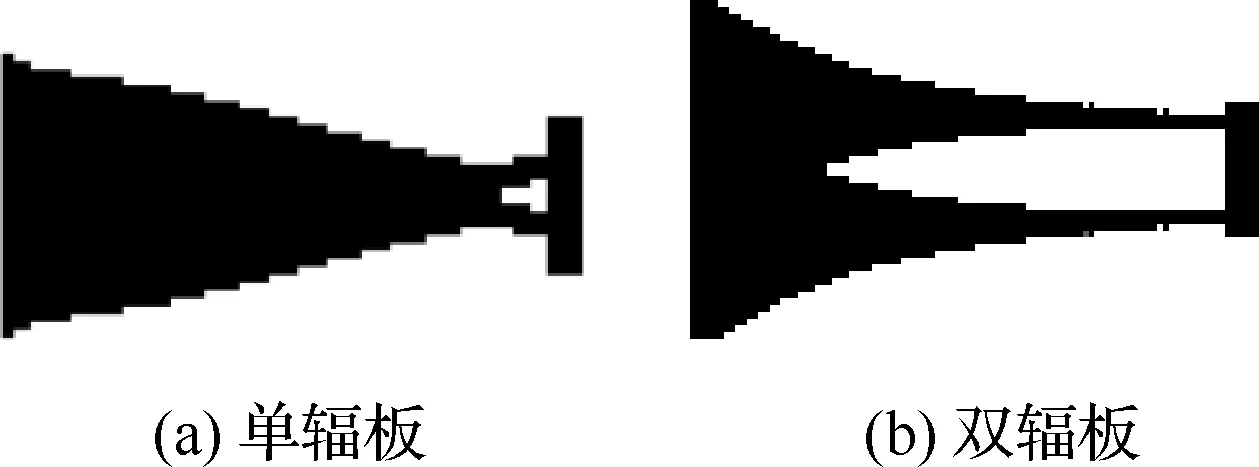
图13 涡轮盘径向截面拓扑结构Fig.13 Topological structure of radial section of turbine disk

图14 涡轮盘结构几何模型Fig.14 Geometric model of turbine disk structure

2种涡轮盘结构在相同约束和载荷条件下的应力和应变能云图如图15和图16所示。由表5可知，在径向截面面积相同的情况下，双辐板涡轮盘整体的质量比单辐板减轻16%。图15显示了单、双辐板的应力分布状况，最大应力均在轮心位置，这与文献[24]得到的结果相同。相比于单辐板，双辐板的最大应力下降了23%。由图16 可以看出，双辐板的应变能分布均匀，整体应变能低于单辐板。

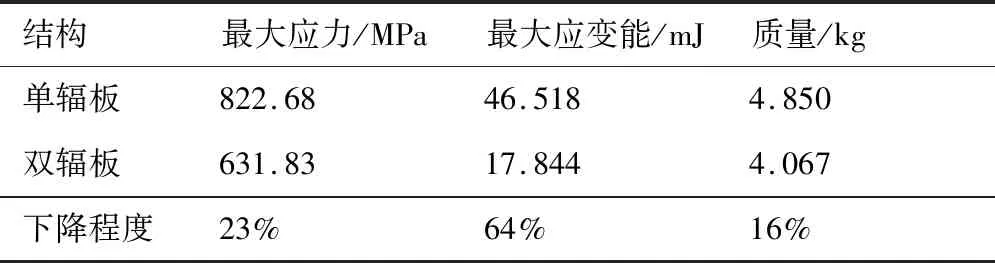
表5 有限元分析结果Table 5 Results of finite element analysis

图15 涡轮盘应力云图Fig.15 Stress distribution of turbine disk

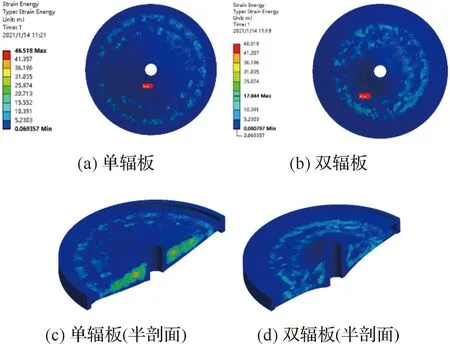
图16 涡轮盘应变能云图Fig.16 Strain energy distribution of turbine disk

5 结 论

1) 针对设计相关载荷拓扑优化中存在的“材料附属效应”问题，运用一种指数型EAMP材料插值模型，并且基于此模型构建了一种新的灰度抑制方法。算例表明，该方法具有单元灰度少、结构清晰、收敛速度快的特点。

2) 对设计相关载荷变密度拓扑优化中存在的目标函数非单调问题，提出一种载荷敏度抑制方法。算例表明了该方法对自重和大惯性载荷下结构拓扑优化的有效性。

3) 应用本文提出的算法对发动机涡轮盘的径向截面进行拓扑优化。通过抑制系数的讨论，说明了设计相关载荷的载荷敏度对涡轮盘的径向截面拓扑结构的影响，揭示了传统单辐板涡轮盘结构与近年广泛研究的双辐板涡轮盘结构之间的演化规律和内在联系。在相同约束和离心载荷条件下对两种结构涡轮盘进行了有限元分析。