五维洛伦兹型忆阻混沌系统及其电路实现
刘 兴 策, 刘 俊 俏
(大连工业大学 信息科学与工程学院, 辽宁 大连 116034)
0 引 言
混沌是一种普遍存在于自然界中的运动状态,它具有很多值得研究的特性,比如:对初始条件敏感性、变化具有随机性、长期行为具有不可预测性。混沌在宏观上虽呈现出无规则的状态,但其本质是一种有序运动。混沌作为非线性科学中的一门前沿课题[1-3],其理论主要起源于对Lorenz系统和Chua系统的设计和研究[4-5]。洛伦兹系统是美国气象学家洛伦兹在模拟天气这一非周期性现象时确定的,根据其研究结果可以得出结论:初期微小的差别随着时间推移差别会越来越大[6-8]。正是这一理论,使洛伦兹系统在非线性系统的研究中具有举足轻重的地位[9-13]。
众所周知,非线性元件是混沌电路中必不可少的一部分。而忆阻器就是非线性元件中的代表。1971年,Chua[14]基于变量组合的完备性原则预测了忆阻器的存在。1976年,Chua等[15]进一步阐述了忆阻器的组成原理和应用特点,并且说明了忆阻器分为磁控忆阻器和荷控忆阻器。由于一直没有发现具有记忆特性的元件,忆阻器的研究一直没有得到科学界和工程界的重视。2008年,惠普实验室首次完成了纳米忆阻器的实现,对忆阻器的研究取得了巨大的进步[16-19]。纳米忆阻器件的出现有望实现非易失性随机存储器,并且基于忆阻的随机存储器的集成度、功耗、读写速度都要比传统的随机存储器优越。忆阻器是硬件实现人工神经网络突触的最好方式。可见,忆阻器在混沌研究中的重要性[20]。
混沌研究虽然历史久远,但将忆阻器应用于混沌却是近些年来的一个研究热点。Muthuswamy等[21]通过用忆阻器来替换Chua电路中的蔡氏二极管,在2008年第一次运用忆阻器构建了混沌系统,并对该电路进行了详细的理论分析与数值仿真。2012年包伯成等[22]将Chua电路中的蔡氏二极管用有源忆阻器模型替代,得到的新混沌振荡电路与传统意义上的混沌电路有很大的不同,包含一些特殊的动力学行为如混沌状态转移等。研究发现,与传统的混沌电路相比,忆阻混沌电路具有更复杂的混沌特性。系统除了对电路参数体现出敏感性外,还依赖于忆阻器的初始值[23-25]。随着忆阻器阶数的增加,忆阻混沌系统的动力学行为就会变得更加复杂。由忆阻混沌电路产生的混沌信号也具有更强的伪随机性,这些特性使其在传统的混沌应用领域混有着更广阔的应用前景[26-28]。因此研究设计更优越的忆阻混沌电路对信息加密和混沌保密通信等各个领域有着非常重要的实际意义。
基于忆阻混沌系统对忆阻器初值敏感性以及在引入忆阻器后系统的动力学行为复杂度增加并且系统的稳定性也会改变的特点[29]。本研究设计了一种五维洛伦兹型忆阻混沌系统。由于在系统中引入了忆阻器,系统的动力学行为变得更加复杂。通过在DSP平台上进行完整的动态分析与实现,验证了忆阻混沌电路的有效性。其简单的电路结构为忆阻混沌系统的分析提供了一种新的研究方法。
1 忆阻器模型
包伯成教授提出的一种新型磁控忆阻器,可以表示为
(1)
电压与电流之间的伏安关系可以表示为
(2)
式中:W(φ)为该忆阻器的忆导,表示电荷与磁通量的关系,单位为西门子。
W(φ)=α+β|φ|
(3)
式中:α和β为忆阻器的系数;φ为忆阻器的磁通量;vs为交流电压源,表示为vs=Asin(2πft),其中A为电压幅值,f为频率,正弦交流电压源vs为忆阻器的输入端,式(3)中的α=0,β=1。当A=19,f分别为5、50 Hz时,忆阻器的伏安特性曲线如图1所示。当使用正弦交流激励时,忆阻器的伏安关系图是一个通过原点的闭合的“8”字曲线。随着f的增加,曲线的旁瓣的面积逐渐减小,这符合忆阻器的基本特性。
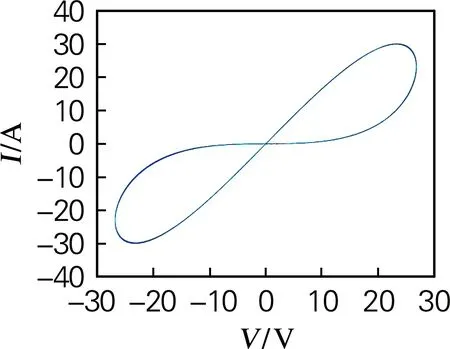
(a)f=5 Hz
2 混沌系统
2.1 混沌电路
一种新型的洛伦兹型混沌电路原理如图2(a)所示,图中的GM是一种新型的忆阻器,其电路原理图如图2(b)所示。
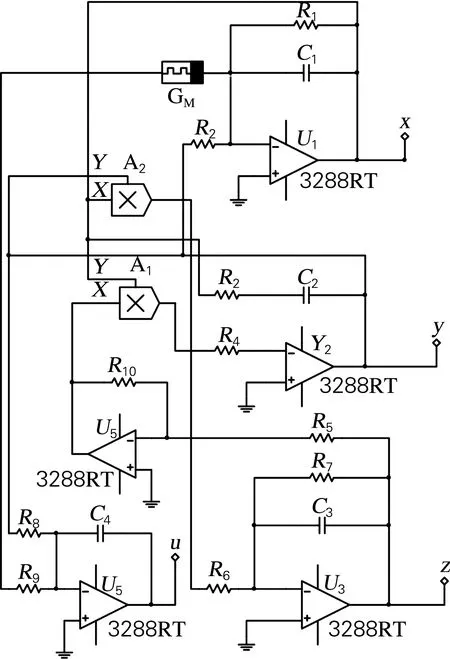
(a)主电路图
电路中各个元件的取值如表1所示:
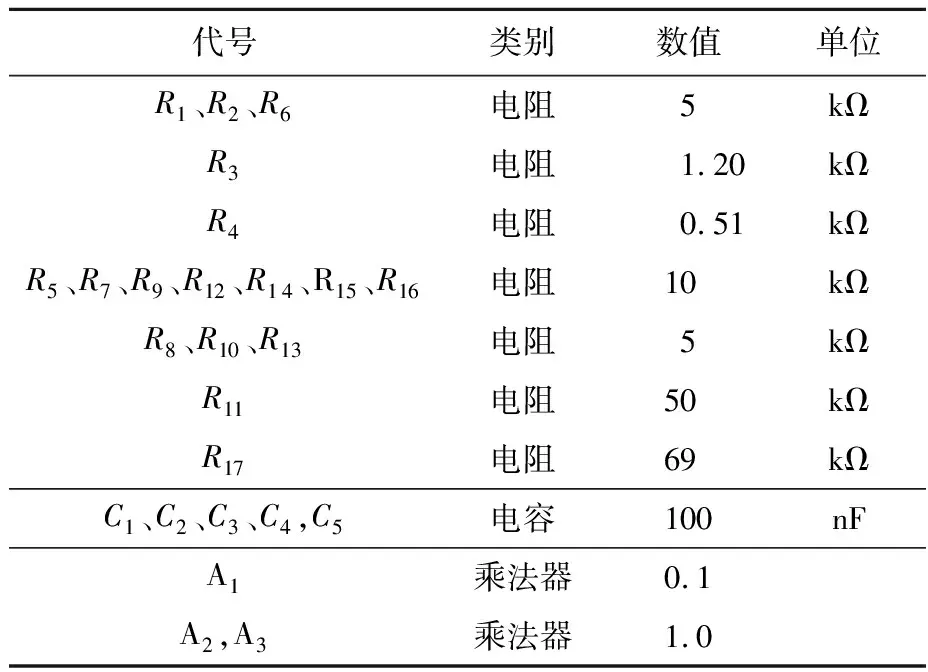
表1 电路元件取值表
图2中的理想磁控忆阻器由电压从动器、反向积分电路、绝对值电路,乘法器和电阻等组成,其数学模型通过分析输入电压和输出电流之间的关系,可以很容易地得到忆阻器输出电流(i)与输入电压(vs)的关系可以表示为
(4)
式中:vw为理想磁控忆阻器的内部变量,g1为乘法器A0的增益,其中k=g1R1/R2,并且忆导W(vw)=kvw/R1。
如图2(a)所示的混沌电路,根据基尔霍夫电压电流定律以及各元件基本特性,可以得出系统方程为
(5)
式中:vx、vy、vz、vu是4个电路变量,vw是理想磁控忆阻器内部变量,g1、g2、g3是乘法器A1、A2、A3的增益,对方程进行无量纲化处理可得
(6)
当系统的参数a=-10,b=-10,c=8,初始条件为(1,1,0,0,0),时间步长为0.01秒,计算出该参数条件下4个李雅普诺夫指数分别为L1=0.696 6,L2=0,L3=-0.167 1,L4=-2.632 1,L5=-20.896 9。对其进行仿真得到的混沌吸引子相图如图3所示。
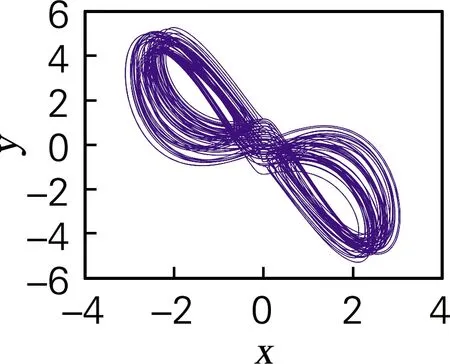
(a)x-y平面
改变系统参数a、b、c并保持初始条件与步长不变,得到以下两类混沌吸引子相图,如图4、图5所示。
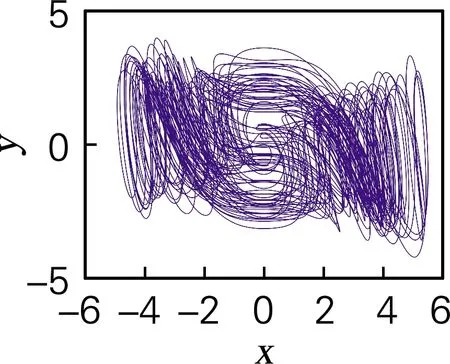
(a)x-y平面

(a)x-y平面
2.2 系统的平衡点分析
根据系统动力学方程可以得到系统的散度可以表示为
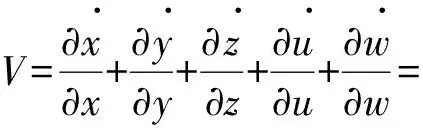
a-c-5-1
(7)
令系统参数a=-10,b=-10,c=8,初值设为(1,1,0,0,0),系统的散度小于零,这意味着系统是耗散的,并且系统可能存在混沌吸引子。令系统方程组式(6)中的各式等于零,可以得到系统平衡点E(0,0,0,0,0),根据平衡点可以得到Jacobian矩阵为
(8)
其特征多项式可以表示为
P(λ)=λ5+13λ4-460λ3+393.559 3λ2+
18 000.009 2λ
(9)
由特征方程可计算出特征值为λ1=0,λ2=5,λ3=-8,λ4=-26.794 5,λ5=16.794 5。由特征方程可知,其系数a0=0,a1=18 000.009 2,a2=393.559 3,a3=-460,a4=13,a5=1。根据劳斯赫尔维兹判据可得,劳斯表中第一列有符号变换,变化的次数等于复平面右半平面根的个数,所以平衡点E(0,0,0,0,0)是不稳定的。
2.3 参数a和c对系统的影响
本系统为五维混沌系统,将分岔图与李雅普诺夫指数谱结合进行分析,可得其不同参数下所处的状态。以参数a和c作为变量,初值为(1,1,0,0,0),步长h=0.01,固定方程的剩余参数,通过改变参数a和c来观察混沌系统不同的状态。
取参数a∈[-10,1],令b=-10,c=8,李雅普诺夫指数谱和分岔图如图6所示。对比李雅普诺夫指数谱和分岔图可得二者可以一一对应。由图6可知,当a取-8.25、-8.15和0时,最大李雅普诺夫指数L1=0,系统此时表现为极限环状态。其他时候,最大李雅普诺夫指数L1始终大于0,L2=0,并且其他李雅普诺夫指数都小于0,所以此时系统表现为混沌状态。
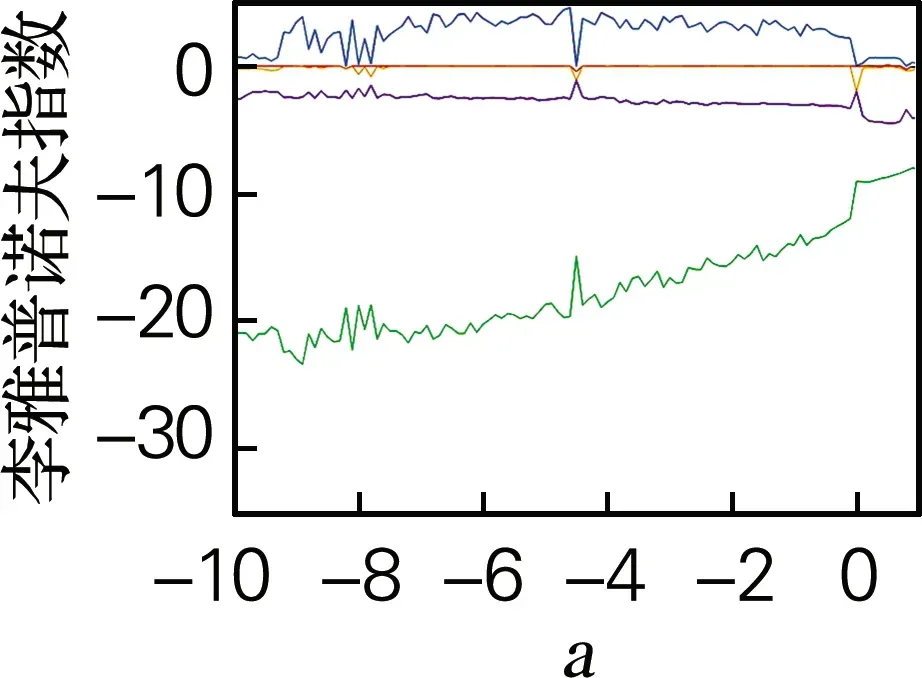
(a)李雅普诺夫指数谱
图7为取参数c=8,b=-10,a分别取-8.25、-8.15、0和-8时x-y的相图,当a取-8.25、-8.15和0时,相图表现为极限环状态,由李雅普诺夫指数谱可知,此时系统有4个李雅普诺夫指数小于0,一个等于0,系统处于周期状态;当a取-8时,相图为混沌状态,此时系统的李雅普诺夫指数中有三个小于0,一个等于零,一个大于0,处于混沌状态。经过分析可知,相图与上文所示分岔图与李雅普诺夫指数谱完全对应。
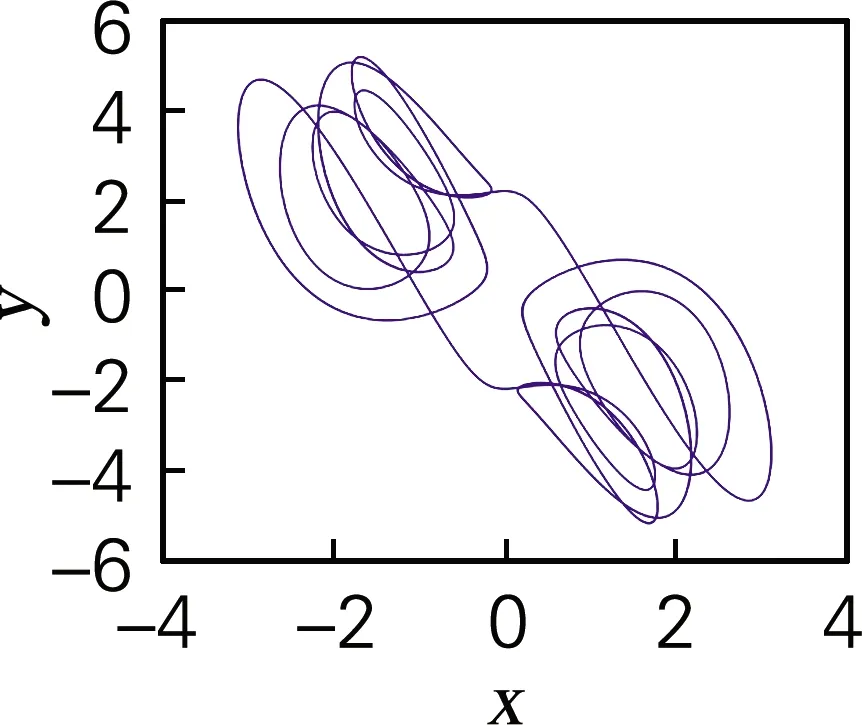
(a)a=-8.25
取参数c∈[0,18]、a=-10、b=-10,该条件下李雅普诺夫指数谱和分岔图如图8所示。对比李雅普诺夫指数谱和分岔图可得二者一一对应。当c∈[0,0.55]时,最大李雅普诺夫指数L1等于0,分岔图中也表现出周期口,所以系统此时表现为极限环。当c=0.55时,系统开始出现混沌现象。当c∈[0.55,8.85]时,最大李雅普诺夫指数L1大于0,并且没有其他指数大于0,此时系统表现出混沌状态。当c∈[8.85,8.9],最大李雅普诺夫指数L1等于0,系统此时表现为极限环。当c∈[8.9,16.9]时,最大李雅普诺夫指数L1大于0,并且没有其他指数大于0,系统表现为混沌状态。当c∈[16.9,18]时,最大李雅普诺夫指数L1等于零,其余各项均小于0,系统表现为极限环状态。
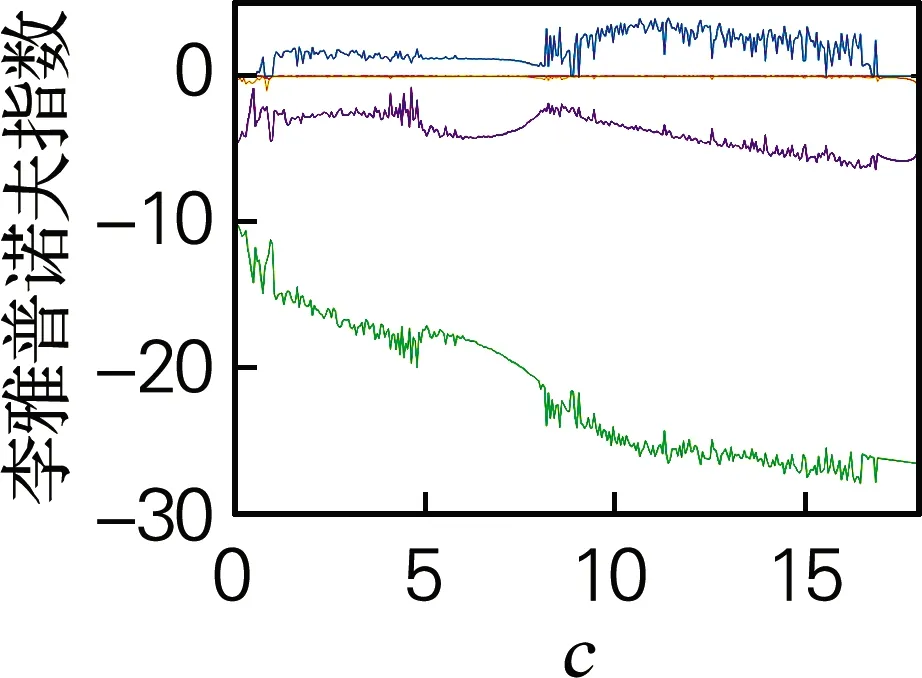
(a)李雅普诺夫指数谱
图9为参数a=-10,b=-10,c分别取0.45、6、8.85、15和17.4时x-y的相图,当c分别取0.45、8.85和17.4时,相图为极限环,由李雅普诺夫指数谱可知,此时系统有四个李雅普诺夫指数小于0,一个等于0,系统处于周期状态;当c取5和15时,相图均为混沌状态,此时系统的李雅普诺夫指数中有三个小于0,一个等于零,一个大于0,系统处于混沌状态。经过分析可知,相图与上文所示分岔图与李雅普诺夫指数谱完全对应。
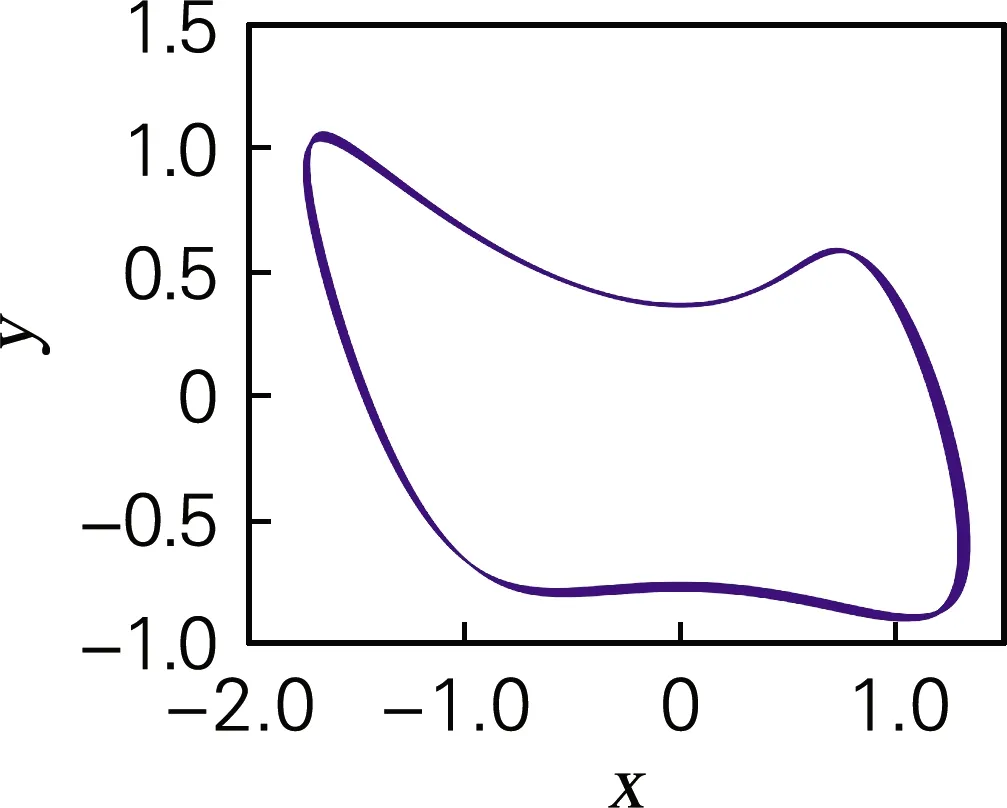
(a)c=0.45
2.4 系统复杂度分析
复杂性的研究涉及各个领域,各领域学者对复杂性的认识也不一样,到目前为止,尚无统一的复杂性概念。混沌系统复杂度是指采用相关算法衡量混沌序列接近随机序列的程度,复杂度值越大,序列越接近随机序列,相应的安全性也就越高。从本质上来讲,混沌系统的复杂度属于混沌动力学复杂性研究范畴。
复杂度分析包含行为复杂度和结构复杂度,行为复杂度是指从混沌序列本身出发,利用一定方法度量短时间窗口内序列产生新模式概率的大小,产生新模式概率越大则序列越复杂。目前,计算混沌伪随机序列行为复杂度的算法比较多,且均以Kolmogorov方法和香农熵为基础,这类算法计算速度快,且结果比较准确,但是如果选取的维数过高或者伪随机序列符号空间过大时,计算结果会溢出,甚至得不到结果。结构复杂度是指通过变换域内频率特性、能量谱特性等来分析序列的复杂程度,序列变换域内能量谱分布越均衡,表示原序列越接近随机信号,即序列复杂性越大,结合香农熵概念即可计算出相应的谱熵值。结构复杂度对变换域能量特征进行分析,其针对的是序列的全部而不是局部,因而与行为复杂度算法相比,其结果具有全局统计意义。本研究利用SE算法和C0算法对结构复杂度进行分析。
SE(谱熵)算法主要采用傅立叶变换,通过傅立叶变换域内能量分布,结合香农熵得出谱熵值。C0算法主要是将序列分解为规则和不规则部分,对其中非规则部分比例进行测量得到结果。以参数c作为变量对系统的复杂度进行分析,取参数b=-10,a=-10,c∈[0,18]时,仿真结果如图10所示。
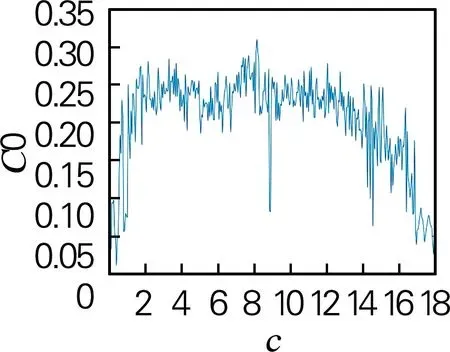
(a)C0复杂度
由图10分析可知,SE算法和C0算法具有高度的同步性,当c<0.55时,系统处于极限环状态,当c∈[0.55,8.85]时,系统处于混沌状态,当c∈[8.85,8.9]时,系统处于极限环状态,当c∈[8.9,17.4]时,系统处于混沌状态,当c>17.4时,系统退化为极限环状态。通过分析SE复杂度图和C0复杂度图可以发现,当系统处于周期态时复杂度处于低点,当系统进入混沌态时复杂度明显增大,所呈现出的结果与图8所示李雅普诺夫指数谱和分岔图相吻合。
2.5 吸引子共存
吸引子共存是一种特殊的现象,主要出现在一些特殊的混沌系统中。在研究非线性系统中,有不可或缺的作用。当保持系统参数不变,而初始值发生变化时,系统轨道可逐渐趋向于点、拟周期、周期或混沌等不同的状态。为了探究这一特殊现象,令a=-10,b=-10,c=5,随着初始值的变化,可以观察到系统状态的变化。数值模拟结果如图11所示,图中蓝色部分表示初始值为(1,2,3,4,10),图中红色部分表示初始值为(1,0,3,4,1)。
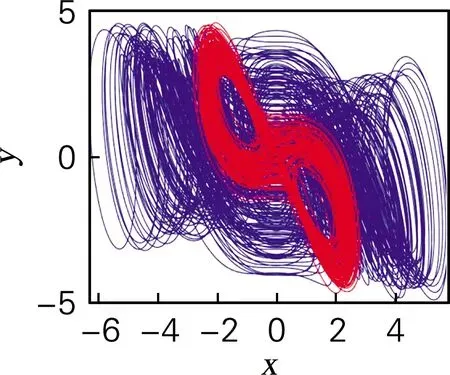
图11 吸引子共存图
3 系统DSP实现
由于混沌系统在使用模拟电路实现时容易受到外部扰动影响,所以在实际电路中的相关特征条件较难准确控制。遂在DSP平台上对本系统进行仿真,使用DSP实现表现出的混沌现象将更加稳定。本研究使用的DSP仿真芯片为f28335,分别设定参数a、b、c,得到如图12所示的图像。
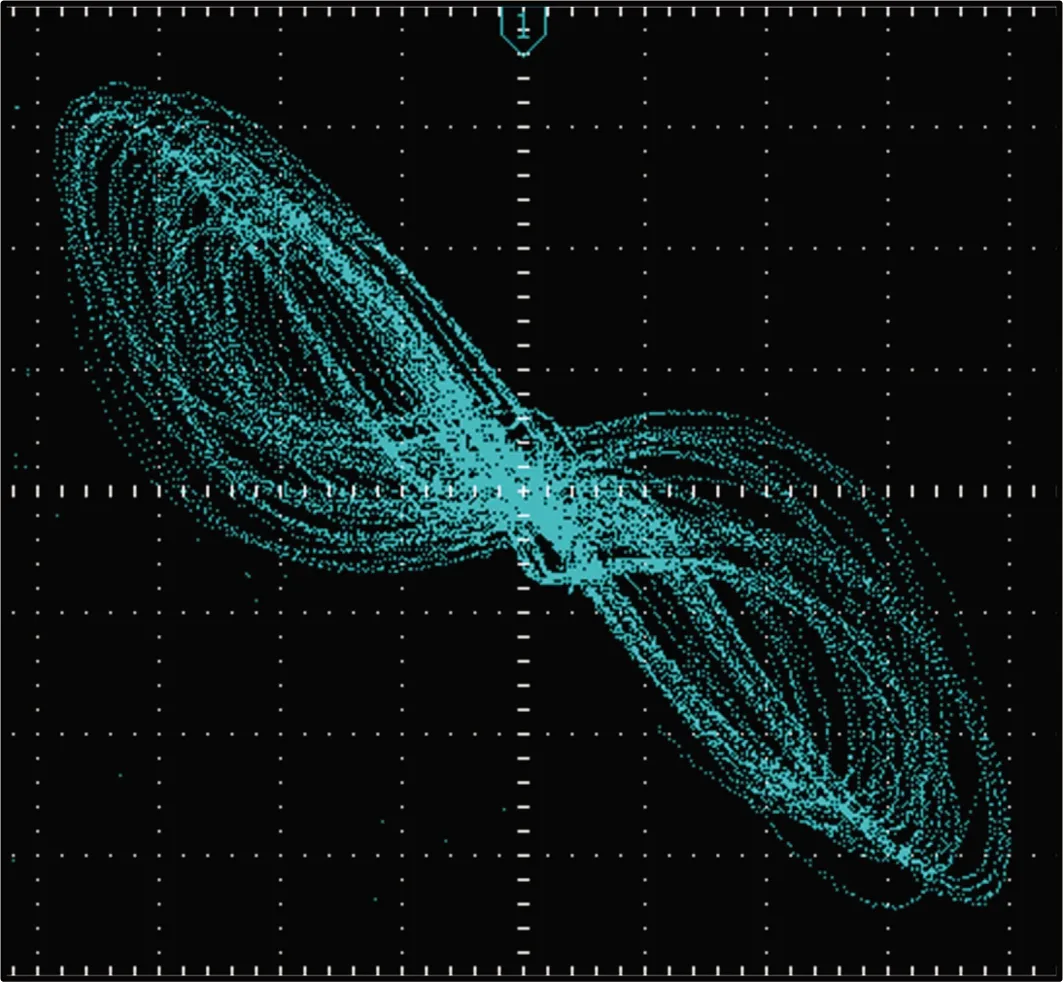
(a)a=-10,b=-10,c=8
4 结 论
设计了一个五维洛伦兹型忆阻混沌电路,并介绍了其无量纲数学模型。在该混沌系统的研究中发现了三种不同的混沌吸引子。通过分析系统的李雅普诺夫指数谱、分岔图、复杂度了解到本系统的动力学特性随着系统参数的变化而表现出了高度的复杂性和敏感性。通过数值模拟,观察到了混沌吸引子共存这一特殊现象。在DSP平台上实现了该电路,并在DSP平台上验证了实验结果与数值分析结果的一致性。由于这些丰富的动力学行为,这种新的洛伦兹型混沌系统在信息加密和安全通信等方面具有良好的应用前景。

