基于折衷规划法的多工况结构拓扑优化设计

叶增沈 王凡超 郑 凯 吴剑国

（1.浙江工业大学 土木工程学院 杭州 310023；2.中国船舶及海洋工程设计研究院 上海 200011）

0 引 言

结构优化设计指的是总体的、目标明确的过程和方法，综合考虑多方面的约束条件，通常以最少的材料、最低的造价或最简单的工序为目标，寻求结构最佳的布设拓扑亦或是形状亦或是尺寸。随着结构优化技术的迅速发展，许多有限元软件（如HyperWorks、Nastran、Ansys 和TOSCA 等）均集成了相应的优化设计模块，这使船舶结构优化设计的应用日趋广泛，解决的问题从减轻结构质量扩展到降低应力水平、改进结构性能和提高安全寿命等更多方面。例如：邱伟强等采用了SIMP法与BESO 法对VLCC 型单纵舱壁进行拓扑优化设计；朱俊侠等、杨玥等采用基于加权和法的多工况优化方法，分别对VLCC 型单纵舱壁、圆筒型FPSO 进行了拓扑优化设计。

由于现实中船舶领域的设计问题通常涉及多个不同工况。对于多工况下连续体拓扑优化设计问题的研究，多采用加权和法进行求解。它采用线性加权法将多工况问题转化为单目标问题求解，实现容易，但对非凸优化问题来说，不能确保得到所有的Pareto 最优解。

折衷规划法（Compromise Programming Method，CPM）已经被证明克服了加权和法的一些缺点：它能在Pareto 边界的非凸区域上找到解。罗震等采用带权重的CPM 针对优化过程中出现的棋盘格等问题进行了研究；范文杰等采用带权重的CPM 对某三段式客车车架进行拓扑优化设计。尽管CPM 可以得到非凸区域上的Pareto 解集，但常规方法需要人为读取优化设计时各个优化目标（如柔顺度） 的最大值与最小值并进行标准差计算，再进行优化软件的相关设置。整个流程中一旦相关设计约束改变，则需要重新对各目标刚度进行读取与计算，耗费大量时间成本。

为此，本文基于CPM 提出了改进的折衷规划法（Improved Compromise Programming Method，ICPM），并基于HyperMesh 软件针对该方法进行了二次开发，以此向设计者提供一组智能Pareto 最优解决方案，节约优化设计的时间成本。应用该技术对海洋工程结构中某悬挑平台纵向框架结构进行了多工况拓扑优化设计，并基于最终拓扑优化构型，从结构设计角度给出清晰的纵向框架构型。

1 折衷规划法的改进

1.1 折衷规划法数学模型

基于结构刚度最大化的拓扑优化是研究在设计域内得到使结构刚度最大（即柔顺度最小）的材料分布形式的问题。每个工况对应一个刚度的最优结构拓扑，一般来说，不同的载荷工况将得到不同的结构拓扑。用带权重的CPM表示多工况下刚度最大化（柔顺度最小化）的目标函数：

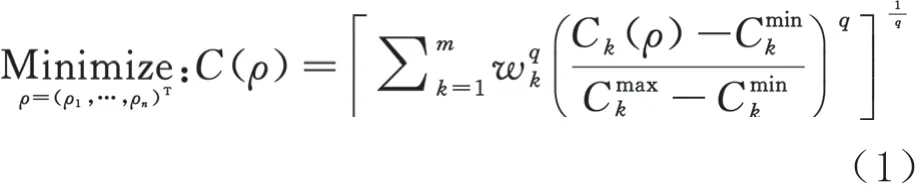
式中：，…，ρ为设计变量；为载荷工况总数；为单元总数；w为第个工况的权值；为惩罚因子，≥2；C（）为第个工况的柔顺度目标函数；C、C为第个工况柔顺度目标函数的最大值和最小值，N·mm。

1.2 改进折衷规划法数学模型

由于传统的折衷规划法时间成本较高，本文提出一种改进的折衷规划法：从设计之初开始，首先确定3个固定的体积分数约束，再分别在3种体积分数下进行单工况拓扑优化设计，并读取出各体积分数约束下不同工况的最大和最小柔顺度值，采用三点线性的方法近似拟合最大柔顺度-体积分数约束折线与最小柔顺度-体积分数约束折线。至此，若设计者想再采用其他体积分数约束时，就不必针对单个工况重新分析并读取最大和最小柔顺度值，只需根据三点双线性插值即可得出各个工况近似的最大和最小柔顺度值，然后立即进行拓扑优化设计而省去了重新计算各个工况的时间。由ICPM结合功效函数法可以得到如式（2）所示多刚度拓扑优化的数学模型：

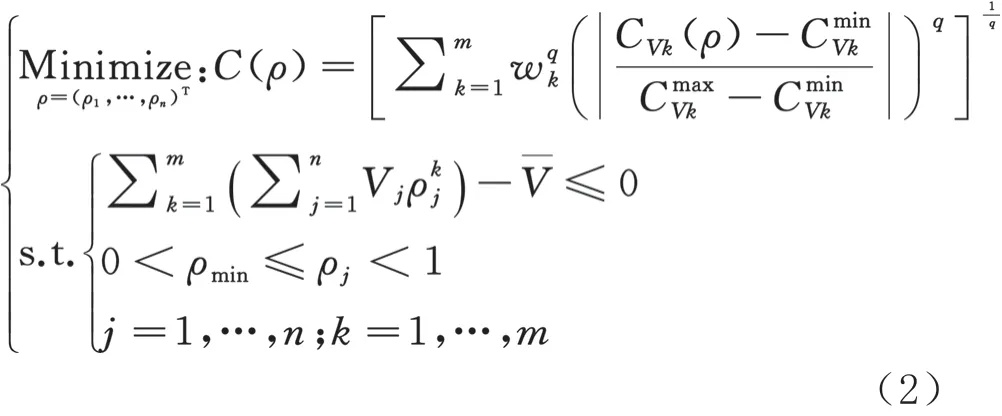
1.3 ICPM与CPM的时间成本对比

以重新优化设计次数（即重新变更体积分数约束的次数）为横坐标，以时间成本为纵坐标。假定计算单工况分析所需要的时间为，计算各工况消耗的时间成本是一致的，工况总数为、优化设计次数为，则CPM进行优化设计所需要的时间为，ICPM进行优化设计所需要的时间为3。很明显，当优化设计次数大于3次时，ICPM极有效地节约了时间成本；而当工况数较多，优化设计次数也越增越多时，ICPM节省的时间成本还会更多。

假定有5个工况，单工况所需的时间成本为2 min，总时间成本-优化设计次数的折线图见图1。

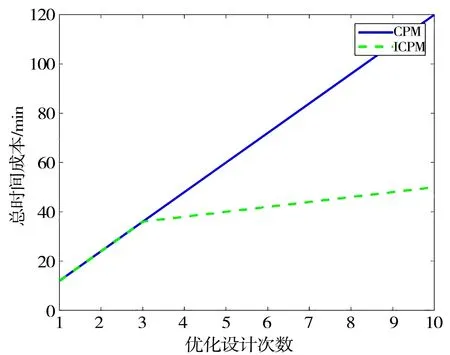
图1 CPM与ICPM的时间成本对比

由图1可见：随着优化设计次数的增加，ICPM相比于CPM节约了大量的时间成本；随着工况、单工况时间成本、优化设计次数的增加，会节约更多时间成本。

1.4 ICPM直接计算验证

为了验证CPM与ICPM在相同的体积分数约束下拓扑优化时均能产生相似的拓扑优化构型，本节采用简单C形板计算模型（见图2）针对ICPM合理性验证。

图2 C形板

工况1载荷沿C形板端部布设（红色标识），工况2载荷沿C形中部布设（绿色标识）。选取体积分数约束为0.30，工况1/工况2权重系数分别取0.40/0.60。拓扑优化结果见图3。

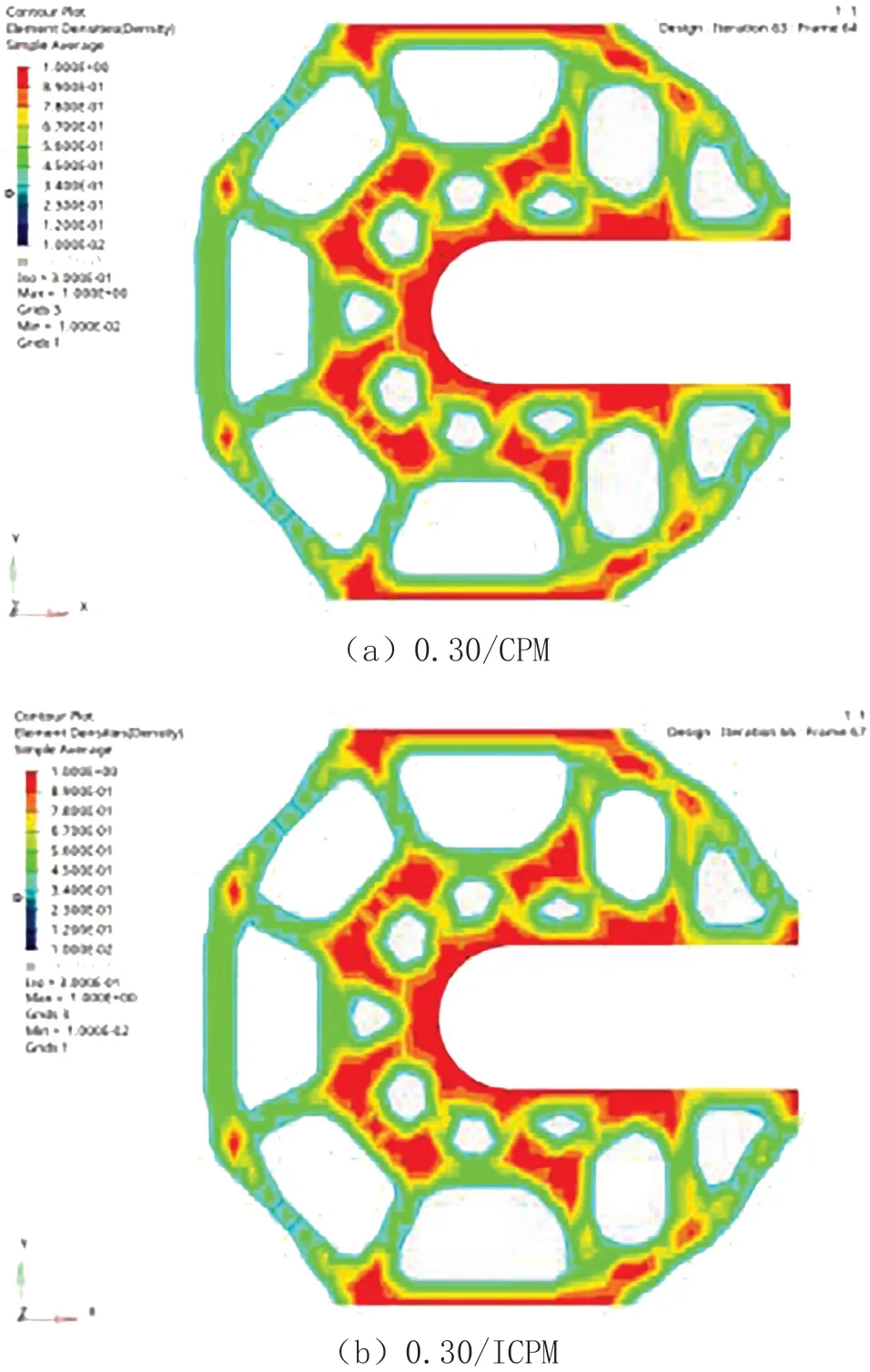
图3 CPM与ICPM优化结果对比

由图3可知：采用双线性插值方法得到的最大和最小柔顺度所构成的多工况化一的ICPM与CPM可得到几乎一致的结果，由此也近一步证明了ICPM的合理性。拓扑优化本身对应着概念设计阶段，在保证构型基本一致的前提下，ICPM最大限度地节省了设计的时间成本，进一步证明了其优越性。

2 改进折衷规划法的二次开发

2.1 ICPM二次开发的主要思路

HyperMesh是Altair公司旗下一款优秀的有限元前处理软件，有着良好的二次开发环境。通过TCL/TK语言，用户可以编写实现特定功能的TCL/TK函数；与此同时，HyperMesh也提供丰富的集成化的内部函数，用户只需要在自己编写的TCL函数中按照指定格式引用这些函数，就可实现某些模块化的功能，比如单元属性的读取、外部文件的读写以及外部执行程序的调用等。

基于ICPM的多工况拓扑优化程序二次开发的主要思路（见图4），首先设立相关界面按钮，记录多工况的数量及名称；其次需要读取各工况的结果文件，获取各工况的最大和最小柔顺度，并计算目标体积分数约束下近似柔顺度的最大值与最小值，为后续编写折衷规划函数打下基础；然后需要编写Dequation自定义函数卡片，并创建DRESP2响应（第二类函数响应）；最终设定该函数响应为目标函数，将多工况拓扑优化问题转换为单一目标拓扑优化问题。

图4 ICPM二次开发的主要思路

2.2 ICPM程序的主要功能

改进的折衷规划法（ICPM）二次开发程序主要包括4个子程序：

（1）读取柔顺度结果子程序，其主要功能是读取优化结果out文件中的最大和最小柔顺度值；

（2）计算柔顺度子程序，其主要功能是根据已读取的3个不同体积分数约束下的最大和最小柔顺度，进行双线性插值估算目标体积分数下的最大和最小柔顺度；

（3）创建Dequation函数子程序，其主要功能是根据各个工况的最大和最小柔顺度自动创建折衷规划函数；

（4）创建响应函数子程序，其主要功能是根据折衷规划函数，设置DRESP2函数响应卡片，对应各数值的实际含义，创建将多工况问题化为单一目标问题的响应，并设为拓扑优化迭代时的目标函数。

2.3 ICPM程序的用户化界面

ICPM程序界面及操作步骤如图5所示。

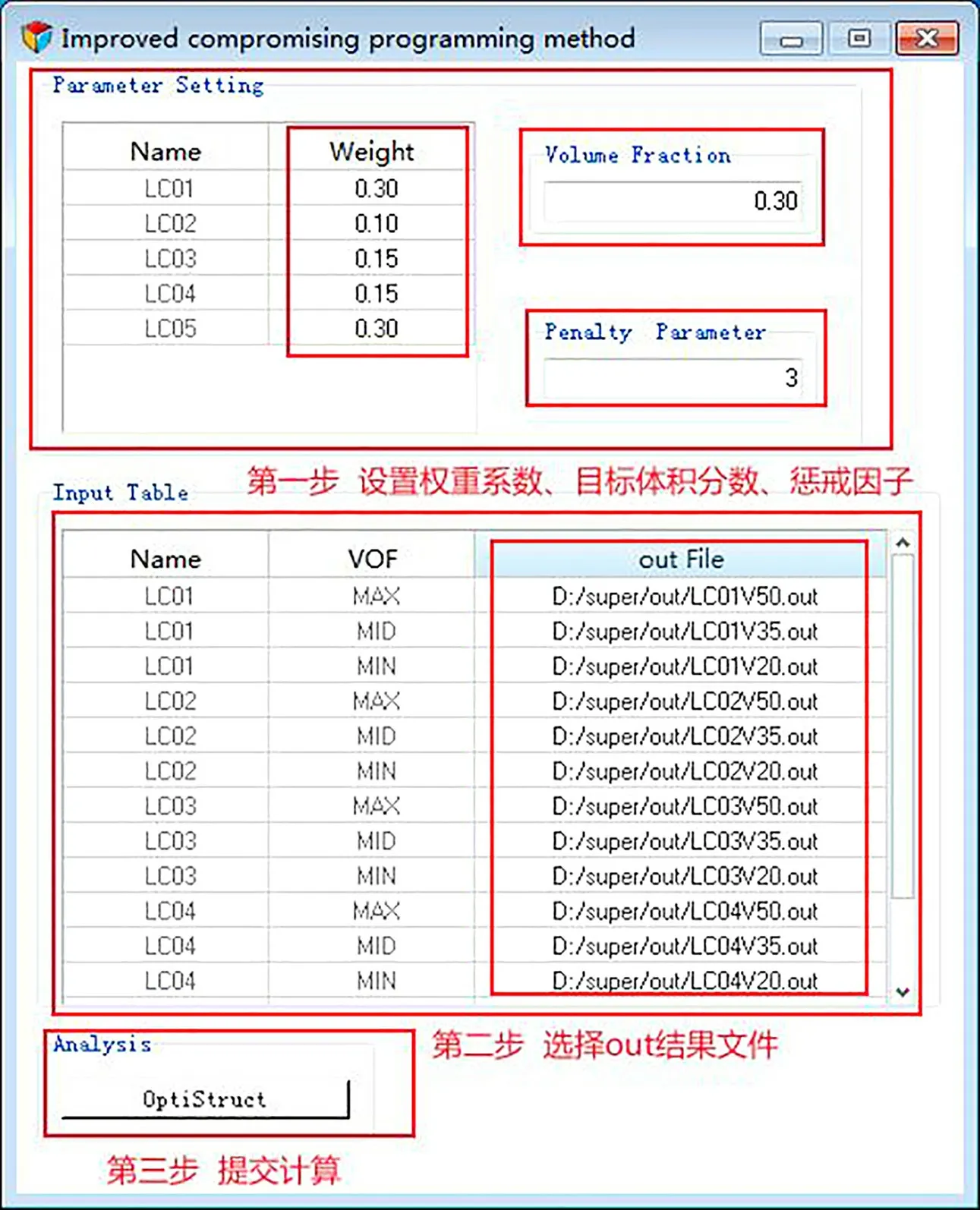
图5 ICPM程序界面及操作步骤

界面的中Parameter Setting模块用于用户设置不同工况权重系数的区域；Volume Fraction模块用于用户设定所需要的目标体积分数约束；Penalty Parameter 模块用于用户设置惩戒因子，程序默认取3；Input Table模块用于用户选择不同体积分数约束下各工况的out结果文件分别针对最大、中间和最小柔顺度；Analysis模块用于提交计算。

ICPM程序在使用上需先确定权重系数、目标体积分数、惩戒因子，接着再选择各单工况分析结果out文件，最终提交计算。

3 结构多工况拓扑优化

3.1 悬臂平台结构有限元模型

海洋工程结构中某平台的有限元模型（隐去甲板），如图6所示，淡蓝色为边界条件。

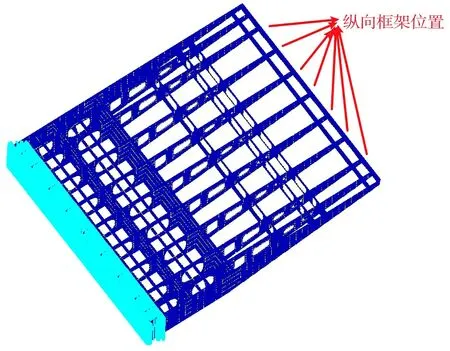
图6 模型纵向框架所在位置

平台模型中板材采用四边形和少量三角形板壳单元模拟，骨材采用梁单元模拟。平台材料均采用低碳普通钢。

3.2 平台结构拓扑优化设计域定义

根据实际工程受力情况，不将平台顶板作为拓扑优化的对象；按照简化工艺的要求，强框间距和纵骨间距通常取值固定，不作为拓扑优化的宏观对象。

平台纵向框架作为平台内的主要支撑构件，主要承受顶板等支撑构件传递而来的载荷。由于平台纵向框架分布较广、占整个平台结构体积较大，会影响其他构件的柔顺度，故对其展开拓扑优化能够较大幅度地改善整个货舱区的应力分布。因此，本文选择的拓扑优化对象为平台纵向框架。

为了提高优化效率，选取中部所有纵向框架设置模式重复制造约束，要求所有中部纵向框架拓扑优化结果一致，拓扑优化纵向框架位置如图6所示。

为了保证拓扑优化传力路径清晰，首先需要将原来构件中存在的开孔进行填实，然后需将纵向框架上所有布设的骨材删除并折算到纵向框架板壳单元的厚度中；除此之外，为保证纵向框架与其他支撑构件的连接性，还需在纵向框架设定最小厚度的非设计区域。

3.3 拓扑优化工况及权重确定

为使拓扑优化结果更贴合实际，本文拓扑优化设计时考虑平台实际的受力情况，分别设定了5个工况，主要分为受均布载荷及受集中载荷。权重系数根据各工况实际的危险程度进行大致评估。拓扑优化载荷布设及各工况权重系数见表1。

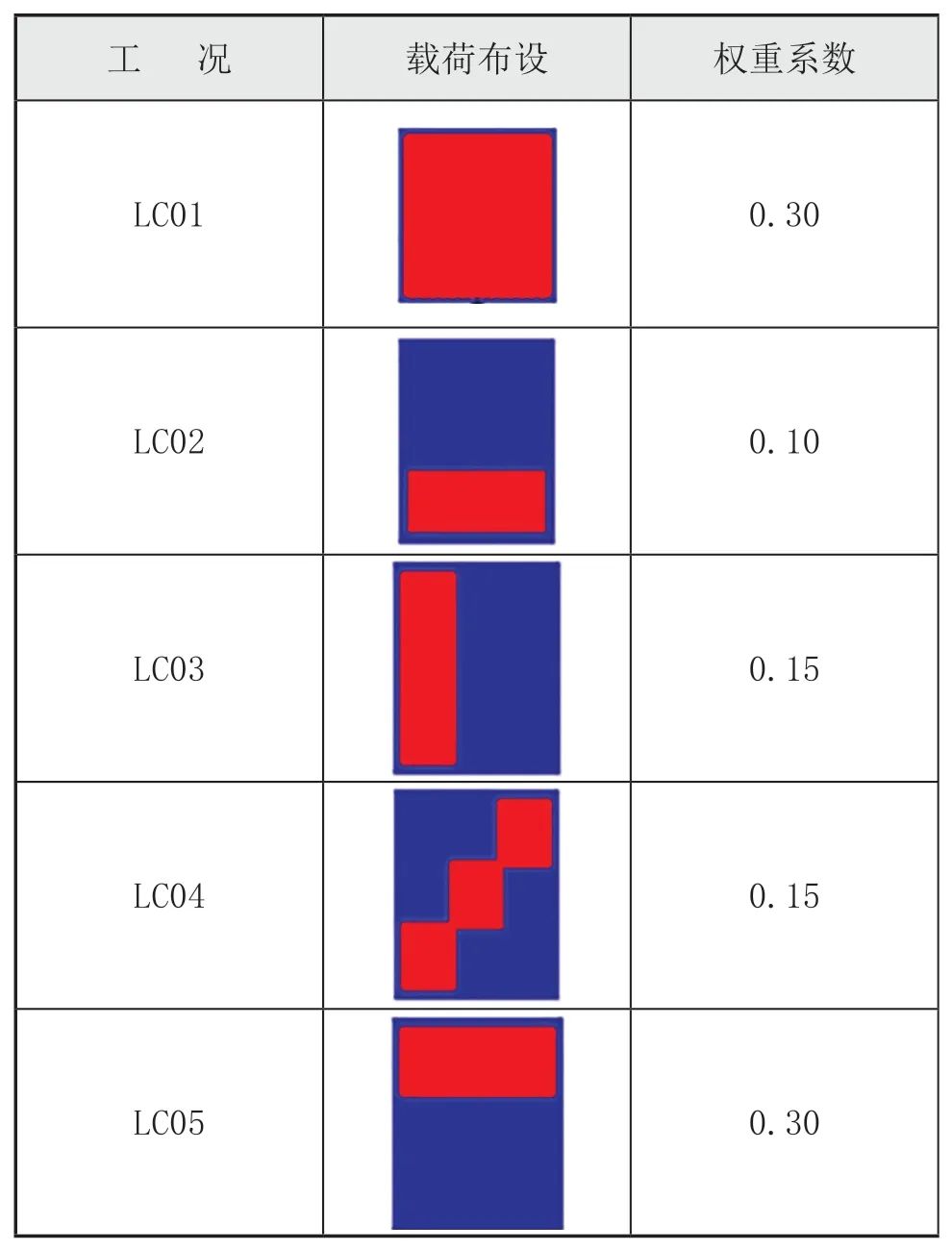
表1 拓扑优化工况及权重（俯视）

3.4 各单工况拓扑优化设计结果

设定不同体积分数约束0.50/0.35/0.20进行各单工况拓扑优化设计，可以得到不同载荷下，纵向框架对应的传力路径，为后续多工况拓扑优化提供支持，具体结果如表2所示。

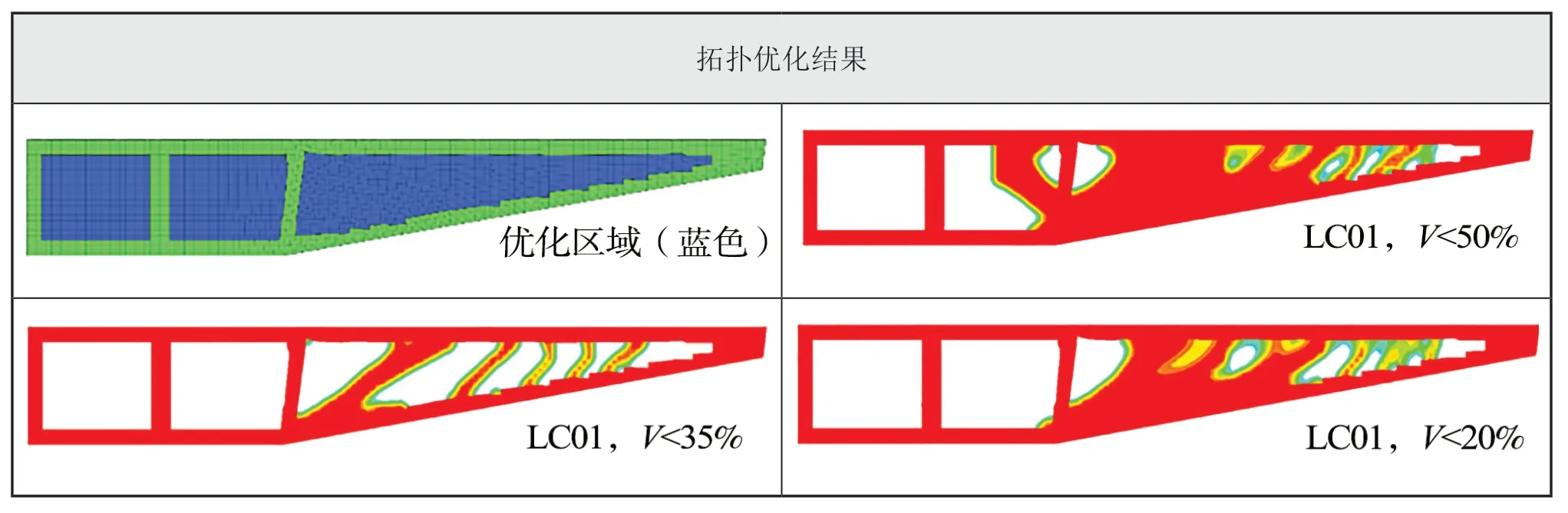
表2 不同体积分数约束0.50 / 0.35 / 0.20 下的各工况拓扑优化结果

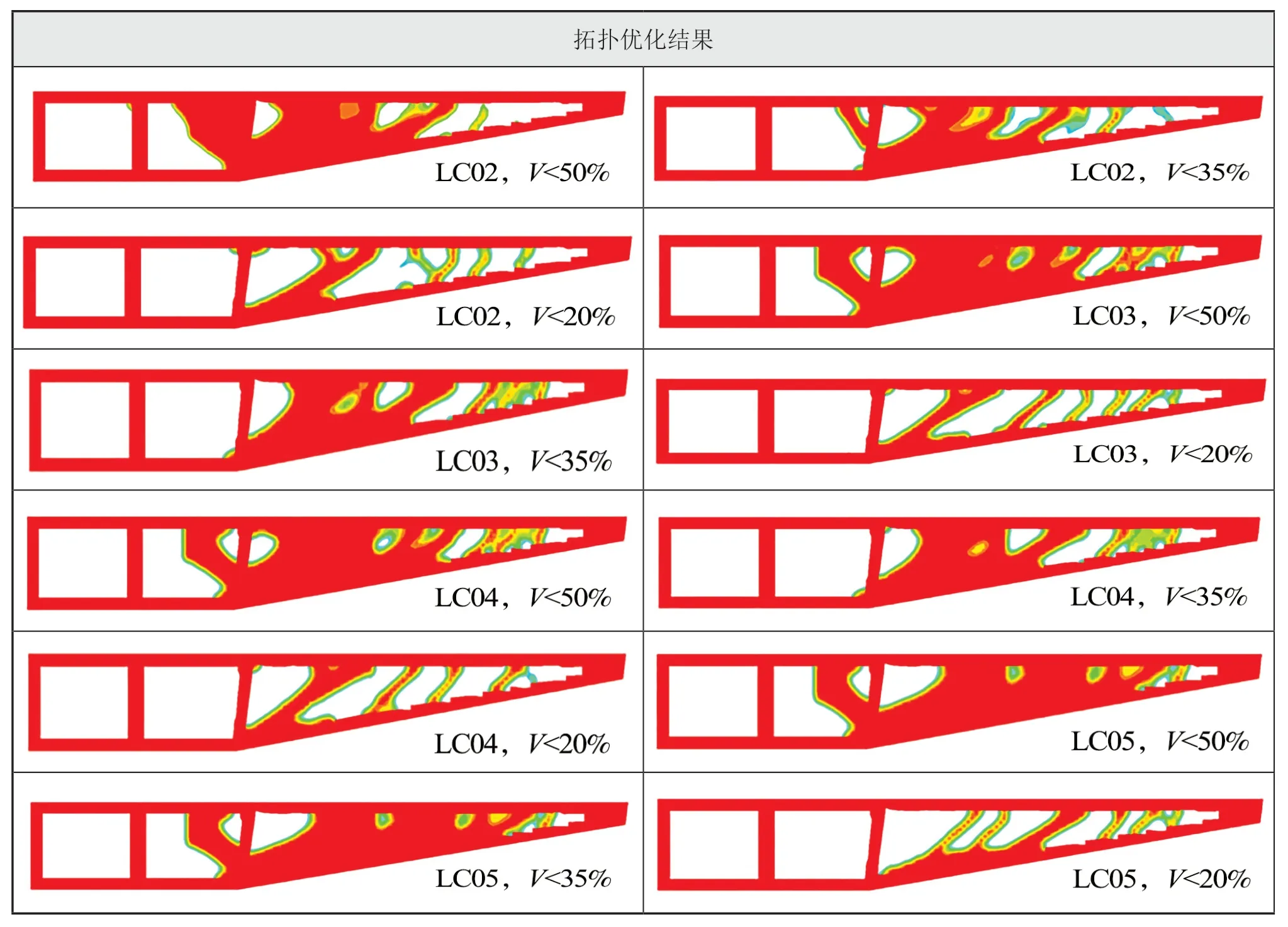
续表2

3.5 各工况结构柔顺度表

各工况下，结构最大和最小柔顺度见表3。

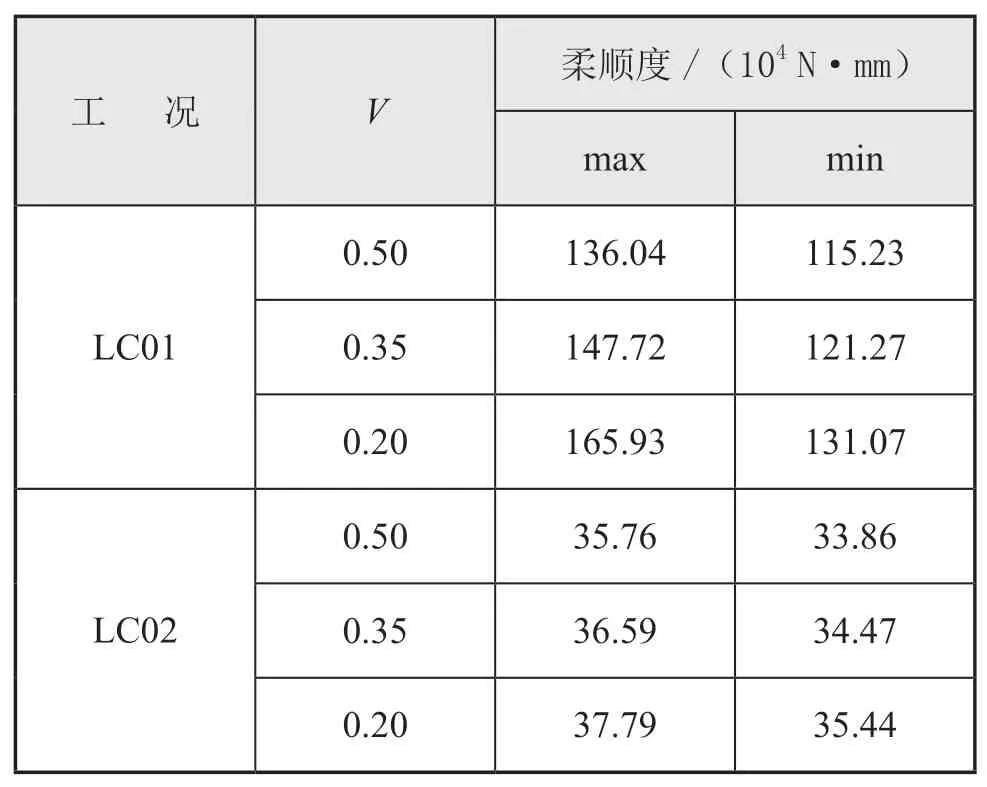
表3 各工况最大和最小柔顺度表

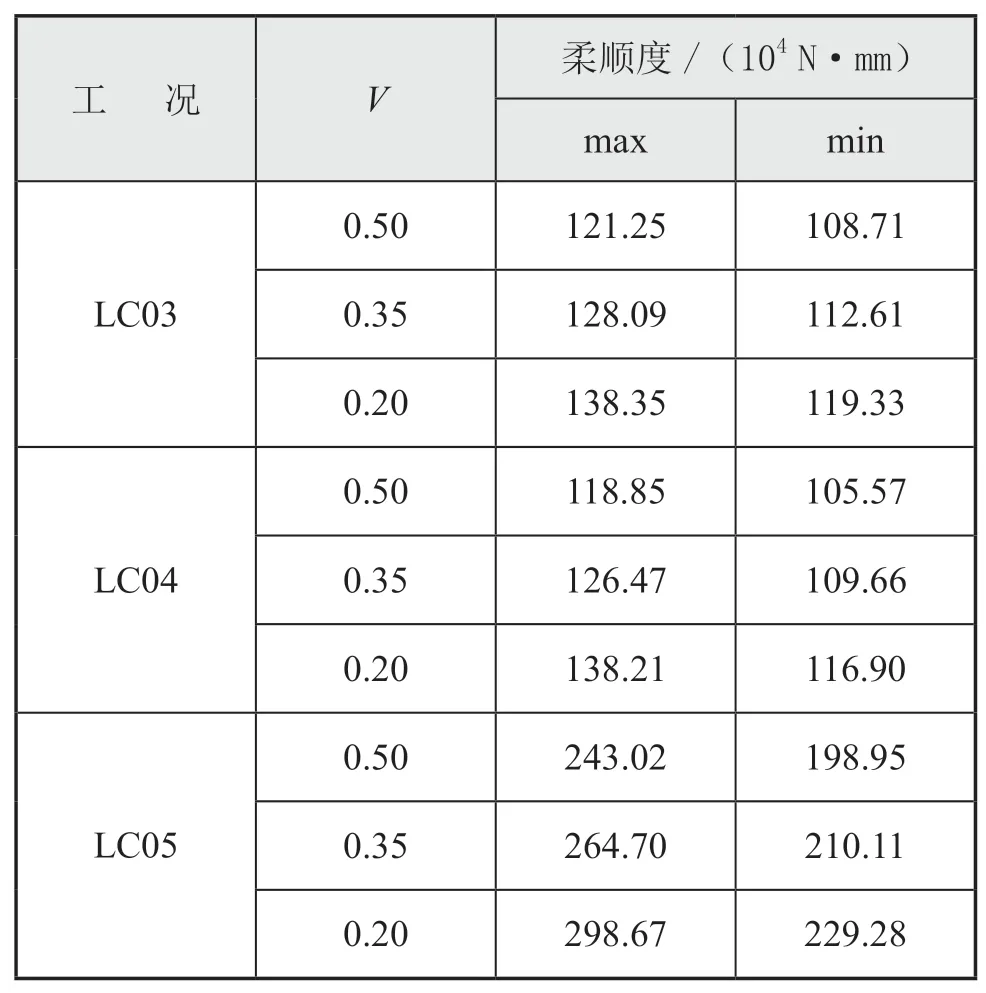
续表3

3.6 不同体积分数约束下拓扑优化结果

通过各工况最大和最小柔顺度表，采用二次线性的方法可以简单计算出不同体积分数约束下的最大和最小柔顺度值，从而省去了各工况再次单独分析的时间。最终针对不同体积分数约束（0.40/0.35/0.30/0.25/0.20），进行了多工况拓扑优化设计，单个工况拓扑优化设计大致为2 min。考虑上述多工况问题，采用CPM需要60 min，而采用ICPM则仅需36 min。

不同体积分数约束的拓扑优化结果见表4。从表4拓扑优化结果可得：不论何种体积分数下，纵向框架端部结构的单元密度基本趋于0，在结构设计时可考虑针对该区域进行适当开孔；纵向框架中部结构也具有明显的可开洞趋势；随着体积分数的减少，纵向框架的尾部结构也逐渐有明显的斜杆出现，可考虑在相应位置设置斜撑或扶强材。

表4 不同体积分数约束下多工况拓扑优化结果

基于0.20 体积分数约束下的拓扑优化结果，本文给出了经拓扑优化后的纵向框架最终设计图，并与拓扑优化前的纵向框架初始设计图纸进行了对比，如表5 所示。

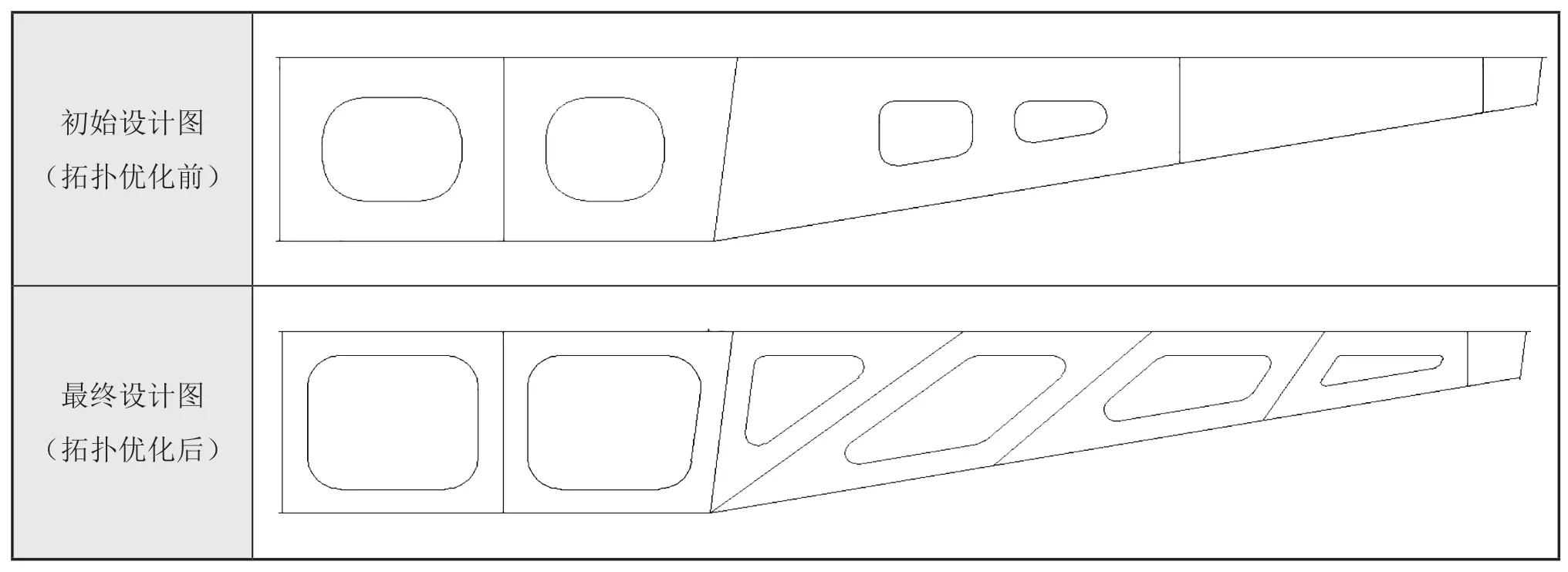
表5 拓扑优化前后纵向框架设计图对比

3.7 不同构型下结构柔顺度、强度对比

基于纵向框架最终设计图，针对模型纵向框架结构部分进行了模型重建，通过设置Compliance响应，读取了各工况下结构的柔顺度，并与实心结构（纵向框架填实）、初始设计结构进行了柔顺度对比，见表6。

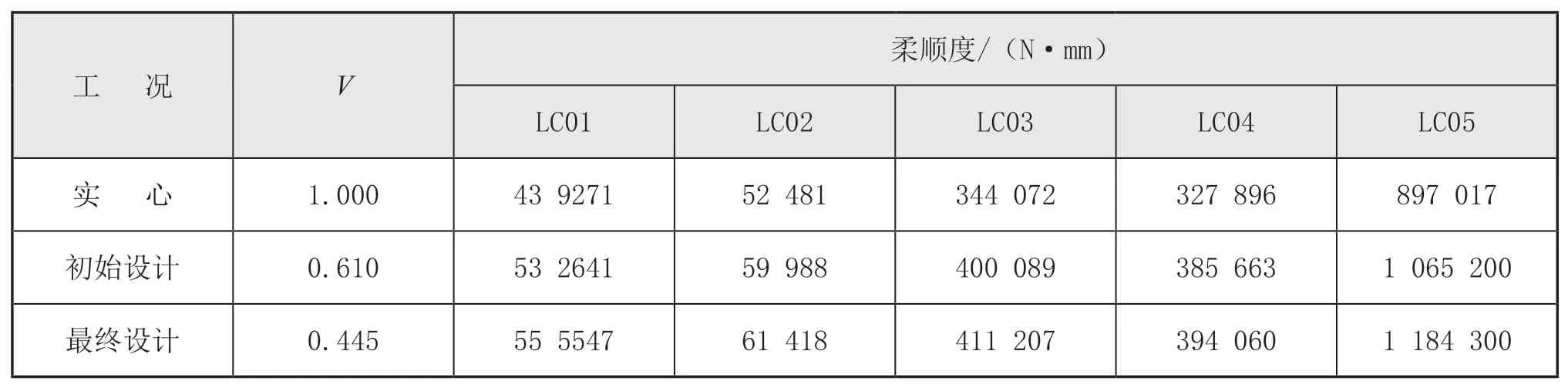
表6 不同构型下结构柔顺度对比

为使优化结果更加直观，读取了3 种设计构型下Von Mises 应力进行强度对比，见表7。

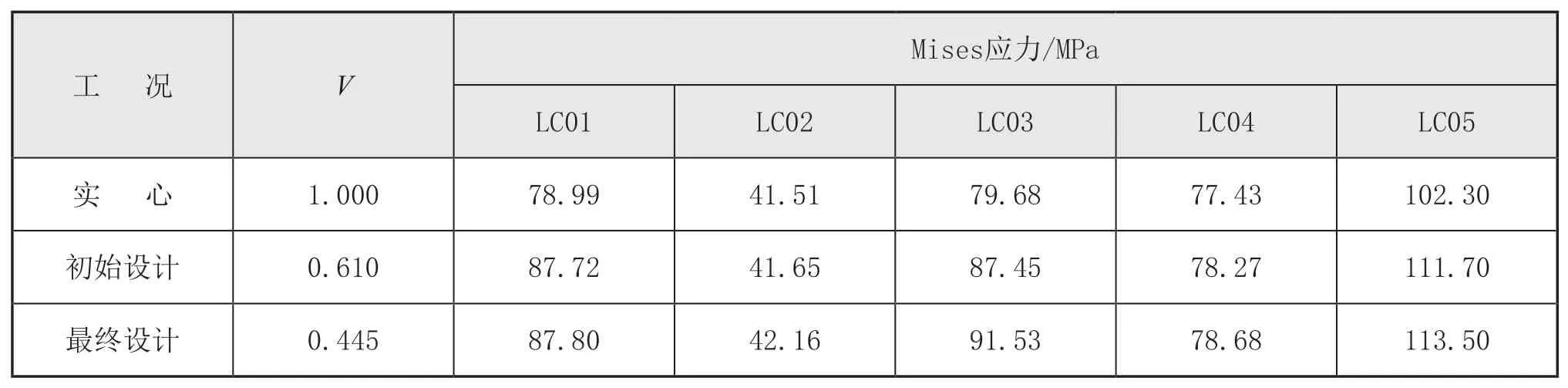
表7 不同构型下结构Mises 应力对比

由表6 和表7 可见，最终设计结构构型相比于初始设计的体积分数降低16.5%，且结构的柔顺度、Mises 应力增加幅度并不明显，进一步证明了拓扑优化方法的必要性与优越性。

4 结 语

本文提出了改进的折衷规划法，并基于Hyper Mesh/OptiStruct商用软件平台进行了改进折衷规划法的二次开发。应用表明:该方法和软件能够帮助设计者找到更为清晰的传力路径，操作性好，可有效节省优化设计的时间，提高工作效率。