基于BP神经网络预测红外-喷动干燥带壳鲜花生水分比

朱凯阳，任广跃,2,*，段 续,2，仇彩霞，李琳琳，楚倩倩，余祖艳

（1.河南科技大学食品与生物工程学院，河南 洛阳 471000；2.粮食储藏安全河南省协同创新中心，河南 郑州 450001）

花生属蔷薇目、豆科一年生草本植物，其中油脂和蛋白质含量最为丰富，同时还含有各种维生素以及钙、磷、铁等微量元素，具有极高的营养价值。花生是豆科植物中一种重要的经济作物，主要生长在干旱和半干旱地区，然而花生的收获季节多在夏季高温多雨时期，采摘后新鲜的带壳花生含水量高，不易贮存，若不及时进行干燥处理，容易使花生再次生芽或者发霉腐败，感染黄曲霉菌，影响食用。通过干燥处理可以延长花生的贮存期，使其更易于运输及后续加工处理。

喷动床干燥可以在物料颗粒干燥过程中提供气动搅拌，这种搅动通过在颗粒表面重建边界层来促进热量传递，同时使物料在床体内做喷泉式往复运动，实现了物料与热空气在床体内有规律的间歇接触。而红外辐射具有热效应好、节能等优点，已被广泛用于粮油、果蔬等农产品的干燥。研究表明，将红外-喷动干燥进行联用能够获得良好的干燥效果。段续等采用红外喷动床对玫瑰花瓣进行干燥实验，研究不同出风温度和风速下玫瑰花瓣的干燥特性并建立干燥动力学模型，为红外-喷动干燥的研究与应用提供了参考；Alizehi等采用红外辐射和喷动床联合干燥胡萝卜，使得胡萝卜具有比普通干燥方法更好的感官特性，热空气和红外辐射的结合形成了协同效应，产生比单独红外干燥或喷动干燥更有效的干燥效果。目前鲜见使用该技术对带壳鲜花生进行干燥的研究报道，因此，可尝试利用该方法对带壳鲜花生进行干燥以获得更好的干燥效果。

物料水分比是干燥过程中一个重要参数，为干燥过程中物料变化的预测和控制提供重要依据。在干燥过程中，物料的水分比具有显著的非线性和时变性，且经过不同程度的处理以后，仅利用单一模型进行拟合，不可避免地存在适应性和预测精确性的局限。近年来，BP人工神经网络（简称BP神经网络）在处理食品加工过程中理化特性与工艺参数之间的复杂关系方面具有较强的适应性和良好的模拟效果。人工神经网络，是通过模仿生物神经网络的行为特征，进行分布式并行信息处理的数学模型。这种网络依靠系统的复杂度，通过调整内部大量节点之间相互连接的关系，从而达到信息处理的目的。BP神经网络属于人工神经网络的一种，是Rumelhart和McClelland于1986年提出的一种误差逆向传播算法的多层前馈网络。BP神经网络具有自我学习和适应的能力，可以通过预先提供的一批相互对应的输入输出数据，分析两者的内在关系和规律，最终通过这些规律形成一个复杂的非线性系统函数，这种学习分析过程被称作“训练”。每个人工神经网络包括输入层、隐含层和输出层，每一层都由几个神经元组成。外界信息从BP神经网络输入层输入，经过隐含层处理，再传到输出层，得到输出值，经过反复学习与训练，输出预期的输出值。BP神经网络在函数逼近、非线性函数拟合和在线预测方面具有良好的适应力，是目前应用最广泛的神经网络模型之一。Akbar等采用人工神经网络对姜黄油产量进行优化和预测，获得了较好的优化和预测结果；巨浩羽等以光皮木瓜为原料对其进行干燥实验，结果表明BP神经网络模型可以很好地描述光皮木瓜的真空脉动干燥过程；李凯旋等采用遗传算法（genetic algorithm，GA）-BP神经网络对蒜香调味粉的制备条件进行优化，结果证明该方法优化后的条件符合实际生产工艺需要；未志胜等基于BP神经网络技术结合GA实现了定向制备鹰嘴豆美拉德风味肽产品，所得参数可以作为鹰嘴豆蛋白美拉德肽产品的最佳制备条件。姜鹏飞等以大西洋鲭鱼为原料，通过人工神经网络研究不同烘烤条件下大西洋鲭鱼水分含量的变化情况，结果表明人工神经网络法能够准确地对大西洋鲭鱼在烘烤过程中的水分含量进行建模。王玉环等采用人工神经网络模型准确预测了油炸外裹糊鱼块的水分含量。

目前鲜见利用BP神经网络预测带壳鲜花生红外-喷动干燥中水分含量变化的研究报道。带壳鲜花生在红外-喷动干燥过程中水分比受到干燥温度、进口风速和助流剂质量等因素的影响，且与其影响因素具有复杂的非线性关系。通过经典的数学模型来预测干燥进程中的水分比，其预测精度随预测对象和条件而变化，且部分数学模型表达式较为繁琐。因此，可尝试利用BP神经网络预测带壳鲜花生干燥过程中水分比变化。本研究通过单因素和正交试验探讨带壳鲜花生在干燥过程中水分比与干燥温度、进口风速、助流剂质量因素之间的关系，使用Matlab R2018a软件建立基于BP神经网络的带壳鲜花生水分比预测模型，以期为带壳鲜花生水分比的在线预测提供进一步的理论依据和技术支持。

1 材料与方法

1.1 材料

新鲜带壳花生（‘海花一号’）产自河南正阳县。挑选大小均匀颗粒饱满的花生，清除泥沙后，放置于网筛中沥水30 min，参考GB 5009.3ü2016《食品安全国家标准 食品中水分的测定》测定初始水分含量（初始水分含量为0.96 g/g），用自封袋封装并放置于4 ℃冰箱中保存备用。选择表面光滑干青豆作为助流剂。

1.2 仪器与设备

红外-喷动装置系本实验室自制，设备示意图如图1所示。设备红外辐射波长范围为2.5～100 μm，红外功率在0～15 kW之间可线性调节。调节轴流风机可以改变物料在喷动床内再循环的速率，出风温度可通过温度传感器测得。

图1 红外喷动床组合干燥装置示意图Fig.1 Schematic diagram of infrared-assisted spouted bed dryer

1.3 方法

1.3.1 带壳鲜花生干燥

试验前通过控制系统调节红外辐射板温度，使喷动床内部达到设定试验温度。将封存于4 ℃冰箱中的带壳鲜花生取出，恢复至室温后将花生和助流剂通过顶盖放入喷动床中，调节变频器，使进口风速达到设定试验值，然后定时定量取出花生测定数据。本研究首先采用单因素试验，因素设置如表1所示。将花生放入红外-喷动床中开始计时，每隔30 min从喷动床中选取做好标记的20 粒花生快速称量后放回，得到的数据记录留用。待花生干燥至安全水分（干基水分含量不大于0.1 g/g）时停止试验。然后，根据单因素试验结果分析确定正交试验因素水平，采用L9(3)正交试验，如表2所示。

表1 带壳鲜花生红外-喷动干燥单因素试验方案Table 1 Experimental scheme of one-factor-at-a-time design on infrared-assisted spout bed drying of fresh in-shell peanut

表2 带壳鲜花生红外-喷动干燥正交试验因素水平Table 2 Code and level of independent variables used in orthogonal array design on infrared-assisted spout bed drying of fresh in-shell peanut

1.3.2 干燥动力学曲线

干燥过程中，测定不同时刻带壳鲜花生的质量，绘制干燥动力学曲线。带壳鲜花生的干基水分含量（/（g/g））按式（1）计算。

式中：m为时刻带壳鲜花生的质量/g；为带壳鲜花生绝干（花生前后两次称量结果差值小于0.002 g）时的质量/g。

红外-喷动干燥过程中带壳鲜花生水分含量用水分比（moisture ratio，MR）来表示，带壳鲜花生中不同时间水分比按公式（2）计算。

式中：m表示任意干燥时刻带壳鲜花生的干基水分含量/（g/g）；表示平衡时带壳鲜花生干基水分含量/（g/g）；表示初始时带壳鲜花生干基水分含量/（g/g）。

由于带壳鲜花生的平衡水分含量远远的小于和m，所以公式（2）可简化为公式（3）。

干燥过程中的干燥速率按式（4）计算。

式中：为干燥速率/（g/（ggh））；X为时刻干基水分含量/（g/g）；X为＋∆时刻干基水分含量/（g/g）。

1.3.3 BP神经网络结构设计

BP神经网络是一种特殊的多层向前型网络模型，主要由输入层、隐含层和输出层3个部分组成。在带壳鲜花生干燥过程中，干燥温度、出口风速、干燥时间和助流剂质量是干燥的重要参数，均对物料水分比有重要影响，因此确定BP神经网络输入层节点数为4，输出层节点数为1。其中，隐含层节点数可以根据公式（5）～（8）确定。

式中：为输入层节点数；为隐含层节点数；为输出层节点数；为0～10之间的常数。

根据式（5）～（8）确定隐含层节点数5＜＜12，通过BP神经网络训练得到不同节点数下的均方误差（mean square error，MSE）结果，确定隐含层节点数。在确定节点数量后，模型由激活函数、求和单元和连接权构成。权值代表连接；通过调整权值的正负来激活或抑制神经元的输入信号；求和单元计算输入信号与权值，最后通过激活函数传递输出。激活函数也称为传递函数，保证神经元输出在[－1,1]或者[0,1]之间。一般情况下，常用的传递函数有3种形式，即线性传递函数purelin，对数S型传递函数logsig以及双曲正切S型传递函数tansig。训练函数主要包括最速梯度下降函数traingd、动量反转的梯度下降函数traindm和Levenberg-Marquardt（L-M）训练函数等。L-M训练函数可以避免传统BP神经网络训练到一定程度时出现的网络麻痹现象，可实现网络的快速收敛，因此，本研究中采用L-M算法作为训练函数。综上，得出建立带壳鲜花生水分比的BP神经网络模型流程图，如图2所示。通过干燥实验得到原始数据，将原始数进行处理后分为测试样本和训练样本输入，输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号，即得到所需的输出结果。

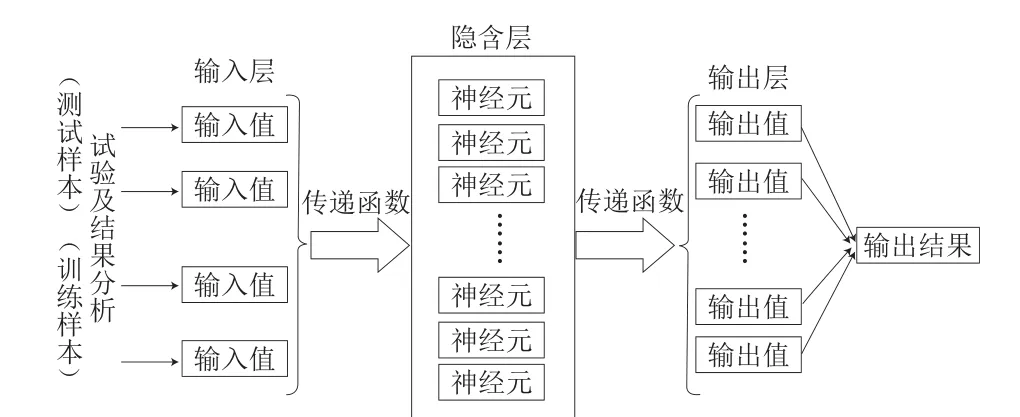
图2 BP神经网络设计流程图Fig.2 Flow chart of BP neural network design

1.3.4 数据采集

采用拟合度和MSE对神经网络模型进行评价。拟合度计算如公式（9）所示。一般来说，越大，所建立的模型拟合效果越好。

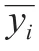
样本MSE的计算如公式（10）所示，MSE越小表示网络模型性能越好。

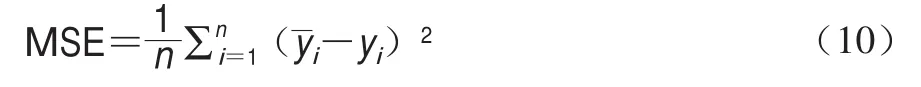
从带壳鲜花生红外-喷动干燥特性实验600 组数据中前480 组数据作为模型输入数据，剩下的120 组数据作为网络模型的测试数据。在选取的数据中，为了减小各个数据间数量级差别，避免因输入输出数据数量级差别较大而造成网络预测误差较大，按公式（11）对原始数据进行归一化处理。归一化处理使其值均在[0,1]范围内，网络模型水分比输出值也在[0,1]内。

式中：为输入数据；为原始数据；为相应指标的最小值；为相应指标的最大值。

1.3.5 模型验证

为了验证建立的BP神经网络的可靠性，利用1.3.4节所获得的数据，选取几种常用的经验、半经验干燥数学模型与该BP神经网络模型进行对比。具体模型见表3。

表3 验证建立的BP神经网络可靠性的干燥数学模型Table 3 Common drying mathematical models used for reliability evaluation of BP neural network

1.4 数据处理与分析

釆用Excel软件对数据进行处理，利用Origin 8.5软件绘图，采用Matlab R2018a软件进行BP神经网络程序编写，并对数据进行分析。

2 结果与分析

2.1 干燥条件对带壳鲜花生的影响

2.1.1 温度对带壳鲜花生红外-喷动干燥特性的影响

在进口风速为16 m/s、助流剂质量为1 kg的条件下，观察不同温度（55、60、65 ℃和70 ℃）对带壳鲜花生红外-喷动干燥特性的影响。由图3A可知，带壳鲜花生水分比随着干燥的进行呈现降低的趋势，并且温度越高，干燥时间越短，水分比降低越快速。由图3B可知，带壳鲜花生干燥速率随着温度的升高而提升。在进口风速为16 m/s、助流剂质量为1 kg、干燥温度为55～70 ℃范围内，初始干燥速率在0.22～0.39 g/（ggh）。温度55、60、65 ℃和70 ℃下，带壳鲜花生的平均干燥速率依次增大，分别为0.06、0.07、0.09 g/（ggh）和0.13 g/（ggh）。在干燥过程中，还存在一个明显的降速阶段，说明在带壳鲜花生的干燥中，水分扩散受内部扩散控制，而内部扩散阻力决定了传质速率。

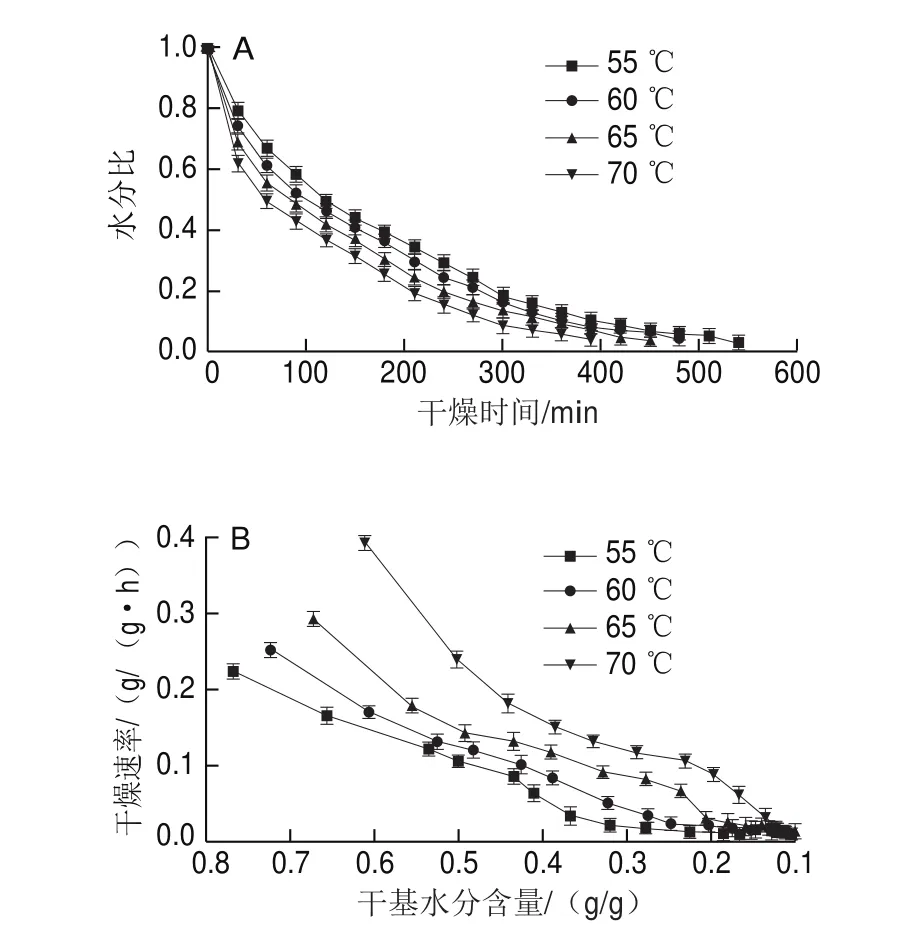
图3 不同温度下带壳鲜花生干燥特性曲线Fig.3 Drying curves of fresh in-shell peanut at different temperatures

温度55、60、65 ℃和70 ℃条件下，带壳鲜花生达到安全水分含量的时间分别为540、480、450 min和390 min。其中60、65、70 ℃与55 ℃相比，所需要的干燥时间分别缩短11.11%、16.67%和27.78%，能耗分别降低6.00%、8.50%和15.00%。综合干燥时间和干燥能耗，选取正交试验温度为60、65 ℃和70 ℃。

2.1.2 进口风速对带壳鲜花生红外-喷动干燥特性的影响

在干燥温度65 ℃、助流剂质量1 kg的条件下，观察不同进口风速（16、17、18 m/s和19 m/s）对带壳鲜花生红外-喷动干燥特性的影响。由图4A可知，带壳鲜花生水分比随着干燥的进行逐渐降低，并且进口风速越高，干燥时间越短，水分比降低越快。由图4B可知，带壳鲜花生干燥速率随进口风速的升高而提升，在干燥温度65 ℃、助流剂质量1 kg、进口风速16～19 m/s范围内，初始干燥速率在0.31～0.47 g/（ggh）。进口风速16、17、18 m/s和19 m/s下，带壳鲜花生的平均干燥速率依次增大，分别为0.07、0.09、0.10 g/（ggh）和0.13 g/（ggh）。

图4 不同进口风速下带壳鲜花生干燥特性曲线Fig.4 Drying curves of fresh in-shell flower at different inlet airflow rates

进口风速16、17、18 m/s和19 m/s条件下，带壳鲜花生达到安全水分的时间分别为450、390、360 min和300 min。其中17、18、19 m/s与16 m/s相比，所需要的干燥时间分别缩短13.33%、20.00%和33.33%，能耗分别降低5.41%、10.81%和18.92%。综合干燥时间和干燥能耗，选取正交试验进口风速为17、18 m/s和19 m/s。

2.1.3 助流剂质量对带壳鲜花生红外-喷动干燥特性的影响

在干燥温度65 ℃、进口风速16 m/s条件下，观察不同助流剂质量1.0、1.5、2.0 kg和2.5 kg对带壳鲜花生红外-喷动干燥特性的影响。由图5A可知，带壳鲜花生水分比随着干燥的进行逐渐降低，但水分比的降低趋势较以不同温度和不同风速为变量缓慢，说明助流剂质量对带壳鲜花生干燥影响程度较小。由图5B可知，带壳鲜花生干燥速率在助流剂质量不同的情况下呈现出不一样的变化趋势。由于干燥初期带壳鲜花生在喷动床内处于涌动状态，因此在助流剂质量1 kg时，花生整体所接触热源的面积较大，此时干燥速率明显高于其他3种助流剂质量组。随着干燥的进行，花生处于喷动状态，助流剂的参与可以给花生带来更好的喷动效果，此时带壳鲜花生的干燥速率随助流剂质量的增大而增大。因此，在助流剂质量这一单因素变量中，带壳鲜花生的干燥速率呈现先降速干燥，然后加速干燥，最后又降速干燥3个阶段。在干燥温度65 ℃、进口风速16 m/s、助流剂质量1.0～2.5 kg范围内，初始干燥速率在0.20～0.33 g/（ggh），助流剂质量1.0、1.5、2.0 kg和2.5 kg下，带壳鲜花生平均干燥速率较为接近，均约等于0.08 g/（ggh）。

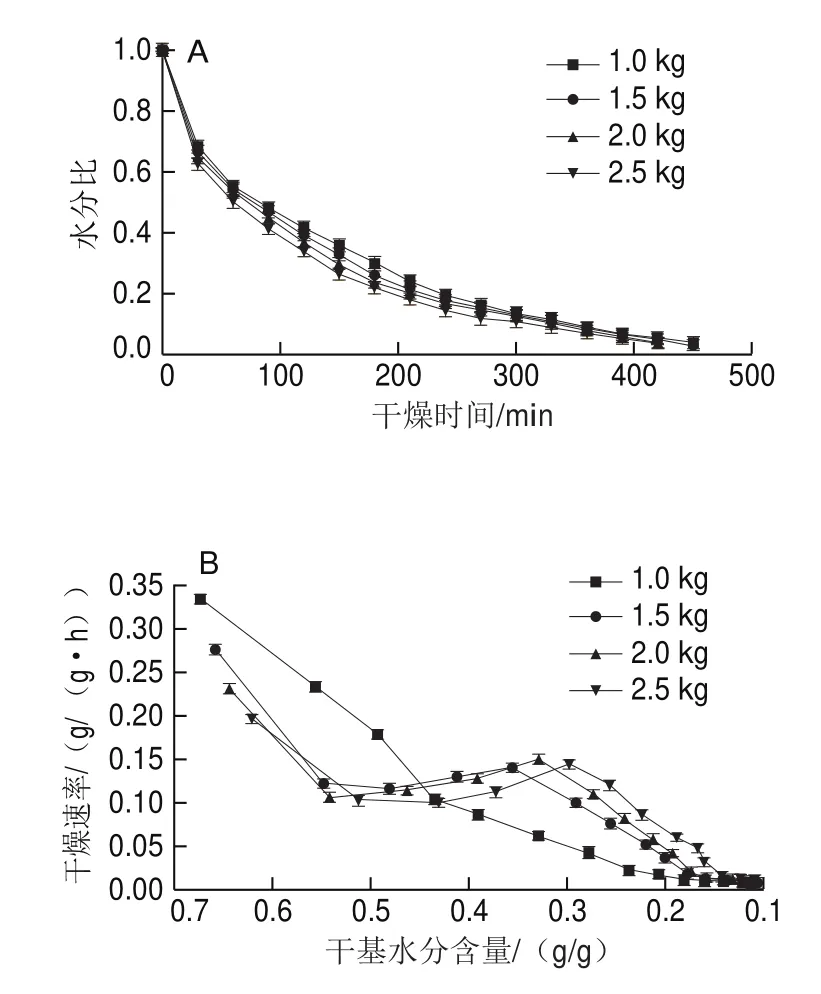
图5 不同助流剂质量下带壳鲜花生干燥特性曲线Fig.5 Drying curves of fresh in-shell peanut with different amounts of glidant

助流剂质量1.0、1.5、2.0 kg和2.5 kg条件下，带壳鲜花生达到安全水分的时间分别为450、450、420 min和420 min。其中2.0、2.5 kg与1.0 kg相比，所需要的干燥时间缩短了6.67%，能耗分别减小7.50%和5.00%。由于在助流剂质量1.0 kg和1.5 kg下二者各项指标相差不大，因此，综合干燥时间和干燥能耗，选取正交试验助流剂质量为1.5、2.0 kg和2.5 kg。

2.2 模型训练与测试

2.2.1 隐含层节点的选择

由前面结果已知，在带壳鲜花生的红外-喷动干燥实验中，温度、进口风速、助流剂质量、干燥时间均对水分比有影响，因此确定该BP神经网络输入层节点数为4。该干燥方式下网络建模的目的是预测水分比，即输出层的节点数为1。

带壳鲜花生红外-喷动试验水分比BP网络建模中采用单隐含层，隐含层节点数在5～12范围内经测试后选取，网络拓扑结构为“4-K-1”。红外-喷动干燥水分比BP网络单隐含层不同节点数的训练逼近图如图6所示。隐含层神经元数目与BP神经网络MSE和训练迭代次数的对应关系如表4所示。

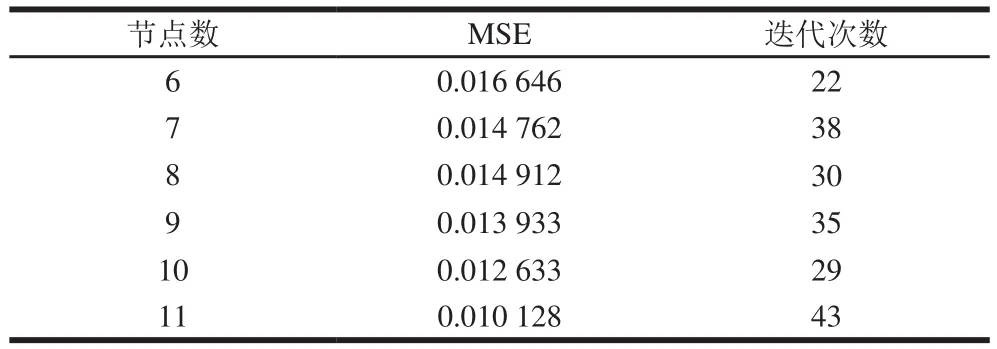
表4 红外-喷动干燥BP神经网络隐含层不同节点训练结果Table 4 Training results for BP neural networks with different nodes in hidden layer

图6 红外-喷动干燥BP神经网络单隐含层不同节点数的MSE曲线Fig.6 Mean square error curves of BP neural networks comprising of different nodes in single hidden layer

当隐层节点数为11时，对应的MSE最小，为0.010 128，训练迭代数为43时，网络训练速度较快。这些结果表明，该条件下BP神经网络模型具有高超的泛化能力；因此选择11为带壳鲜花生红外-喷动试验BP神经网络模型单隐层节点数。

2.2.2 网络模型训练

从600 组样本数据中，随机抽取480 组作为训练样本数据，剩余120 组作为测试数据，通过BP神经网络进行训练，进行水分比分布曲线预测。在BP神经网络中，输入层试验数据经过归一化处理后输入系统；隐含层节点数选择11，输入层到隐含层的传递函数为tansig-purelin函数；设置该BP神经网络的学习速率是0.06，迭代次数为1 000，收敛准则为0.000 001，通过不断调整权值和阈值，达到预测的效果。在确定网络模型的结构后，开始对模型进行训练。如图7所示，在迭代训练41 次之后，获得满足误差条件的稳定预测模型，并停止训练。在验证过程中，BP神经网络模型在第35代表现出最佳的验证性能，MSE最小，为0.002 010 8。

图7 均方误差曲线Fig.7 Mean square error curves

神经网络必须对新数据具有高度的可预测性，在训练中，图8反映了4 组试验值和预测值之间的回归拟合情况，实线和虚线结果表明试验值和预测值之间线性拟合良好。BP神经网络模型训练集的拟合度为0.995，验证集的拟合度为0.995，测试集的拟合度为0.994。所有样品试验值和预测值的拟合度均高于0.995，表明优化后的模型与训练数据吻合，BP神经网络模型预测的拟合度均大于0.99。

图8 带壳鲜花生红外-喷动干燥BP网络训练回归图Fig.8 Fitted curves of fresh in-shell peanut obtained from BP network training

2.2.3 模型测试

将实验测得的数据输入训练好的模型进行仿真验证。图9显示了神经网络的预测误差曲线（误差＝实验值－预测值）。由图9可知，在用于测试的干燥样本中，大部分数据集中在±0.04之间，其中39.17%的误差为负值，表明预测值略小于实验值；60.83%的误差为正值，表明预测值略大于实验值。其中最大误差6.43%，最小误差0.02%，平均误差3.23%，三者均在误差允许的范围内。经计算，实验值与预测值之间的决定系数为0.99，MSE为0.02，可见BP神经网络具有很高的预测精度，能够很好地预测带壳鲜花生在干燥过程中的水分比。此外，如果红外-喷动干燥过程中的外部环境参数和带壳鲜花生本身的相关参数已知，则训练后的神经网络模型可以用于预测水分比的变化，从而消除了复杂的实验检测过程，节省大量的时间和成本。

图9 带壳鲜花生红外-喷动干燥样品水分比误差曲线Fig.9 Moisture ratio error curve of fresh in-shell peanut dried by infrared-assisted spouted bed drying

2.3 模型验证

本实验选取7种薄层干燥模型对不同温度、不同进口风速和不同助流剂质量进行数据拟合，相应的、和模型参数值见表5。

表5 不同干燥模型的干燥系数及模型参数Table 5 Drying parameters and model coefficients of different drying models

续表5

通过计算对比表5中7种数学模型的、，可以看出，扩散模型与Newton模型的模型评价指标平均值分别为0.928 2和0.938 8，因此，这两种模型不适合描述带壳鲜花生红外-喷动干燥样品中水分比的变化规律；Midilli模型和对数模型对实验数据的拟合度较高，其模型评价指标的平均值分别为＝0.997 9、＝0.000 8和＝0.991 6、＝0.004 7。Midilli模型平均值略大于对数模型，并且Midilli模型中比对数模型中更小。因此，选用Midilli模型描述带壳鲜花生红外-喷动干燥的水分变化规律。

通过全面的数据分析得出较为适合的数学模型，此时以干燥温度60 ℃、进口风速18 m/s和助流剂质量2 kg为例，对比Midilli模型与BP神经网络预测水分比的相对误差值，结果如表6所示。

表6 红外-喷动干燥带壳鲜花生水分比的实验值与预测值Table 6 Experimental and predicted values of the moisture ratio of fresh in-peanut dried by infrared-assisted spouted bed drying

由表6数据可知，Midilli模型多数实验值与预测值吻合效果较好，整体效果基本达到预测的目的，预测值与实验值间的决定系数为0.976 1，平均相对误差为14.17%；而BP神经网络模型预测值与实验值间的决定系数为0.996 3，平均相对误差仅为4.38%。BP神经网络模型预测所得平均相对误差低于Midilli模型，说明BP神经网络预测准确度更高。因此，基于BP神经网络的带壳鲜花生红外-喷动干燥水分比模型可以有效地预测带壳鲜花生干燥过程中的水分比变化。

3 结 论

通过带壳鲜花生红外-喷动干燥单因素试验可以看出，干燥温度和进口风速越高，红外-喷动干燥带壳鲜花生水分含量变化越快。对采用大量实验数据建立“4-11-1”拓扑结构的BP神经网络模型进行训练和测试，结果得到决定系数为0.99，MSE为0.02。表明该BP神经网络对带壳鲜花生红外-喷动条件下干燥水分比预测效果良好。带壳鲜花生干燥异于普通薄层干燥，通过对比传统经典数学模型与BP神经网络模型可知，由于物料的特殊性，BP神经网络模型预测数据的准确度高于传统数学模型，其预测的相对误差相较于传统数学模型减少了9.79%。综上，基于BP神经网络的水分比预测模型在预测带壳鲜花生干燥过程中水分比变化规律方面更具优势。

BP神经网络能够将物料干燥过程中所有影响因素整合于一个网络模型中，具有便捷性和准确性等方面的优势，可在食品干燥相关研究领域中进行广泛应用。本研究所建立的基于BP神经网络的带壳鲜花生红外-喷动干燥模型能够较好地对带壳鲜花生干燥过程中水分比进行预测，研究结果可为带壳鲜花生红外-喷动工艺的优化提供新的研究思路和技术参考。