深厚覆盖层地基渗流稳定有限元分析
吕德浩
(林口县移民安置服务中心,黑龙江 林口 157600)
0 引 言
渗流控制包括理论研究和技术措施,控制理论是防排渗和反滤层结合的理论研究,技术措施是研究坝体混凝土面板、心墙等防排渗措施[1]。在地基方面,主要表现为水平铺盖、混凝土防渗墙、帷幕灌浆等措施。渗流控制主要为了降低大坝坝基渗漏量,确保坝体及地基的渗透稳定性。
1 有限元原理
1.1 单元剖分及渗透矩阵
设单元e的三结点坐标依次为(xi,yi)、(xj,yj)、(xm,ym),水头函数值为hi、hj、hm,则水头h在以i、j、m为顶点的三角形内的线性插值函数为:
h(x,y)=α1+α2x+α3y
(1)
水头函数为:
hi=α1+α2xi+α3yi
hj=α1+α2xj+α3yj
hm=α1+α2xm+α3ym
(2)
用△表示三角形的面积:

(3)
得单元e上的水头表达式为
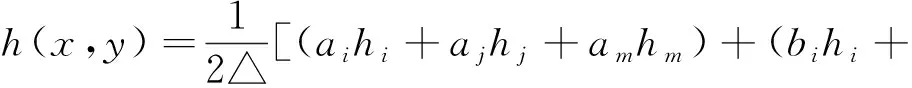
(4)
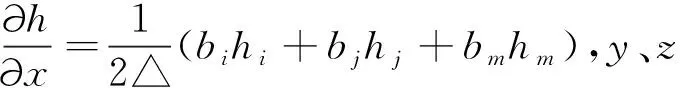
1.2 渗透矩阵调整法求解自由面
有限元法求解应确定渗流区域边界定,求解步骤具体如下[3]:
1)估算一条渗流自由面,划分有限单元法的计算区域。
2)网格划分计算区域,边界条件为设定的渗流自由面,计算渗流区域内结点水头值。
3)渗流自由面上的单元经二次迭代后不再参与计算,故将该单元渗透矩阵乘以定值1.0×1015m/s。
4)二次迭代后进行求解,并判断两次的结点水头值差值:
(4)
式中:i为迭代次数;j为结点编号;ε1为结点水头差值。
当渗流区域内结点均满足差值要求时,则区域内节点连线为自由面。
(5)
式中:H、Z为结点水头和位置势;ε2为收敛判别参数。
2 工程算例
2.1 平面算例一
设定各向同性且均质介质矩形断面高10 m,宽10 m,上游水位为10 m,下游水位为2 m。计算模型尺寸示意及网格剖分见图1、图2。

图1 计算模型示意图 图2 有限元网格剖分图
该算例用加密高斯点法、复合单元法和渗透矩阵调整法求得的浸润线位置如表1所示,流速矢量图和水头等值线图见图3、图4[4]。
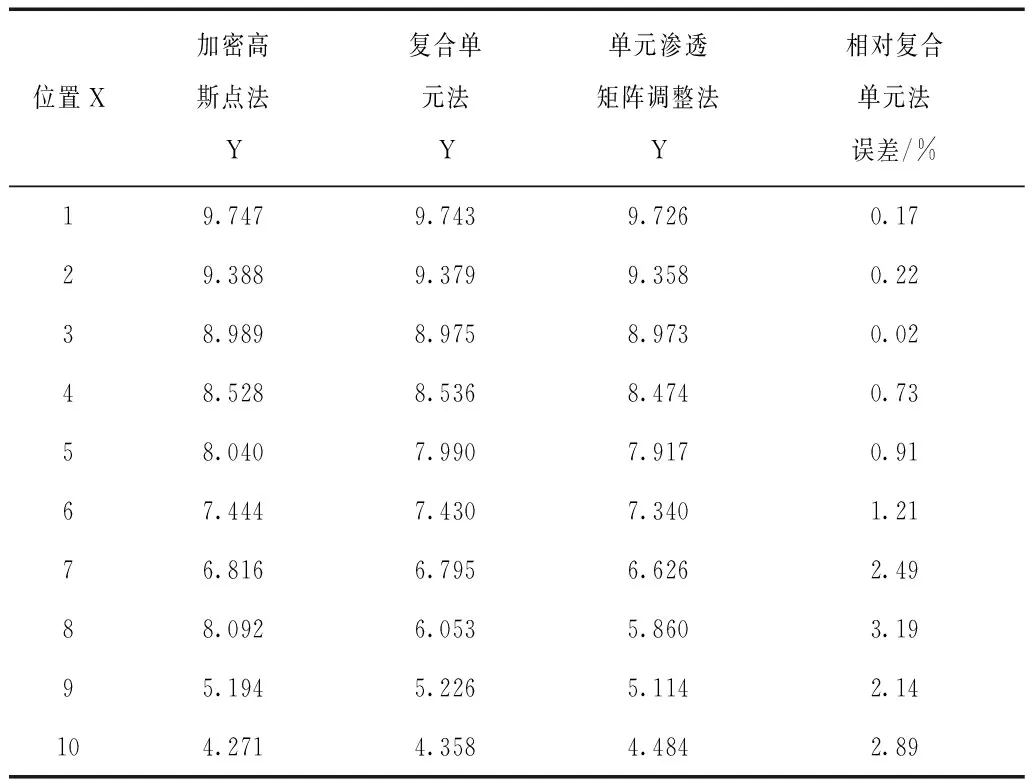
表1 渗流浸润线位置求解比较
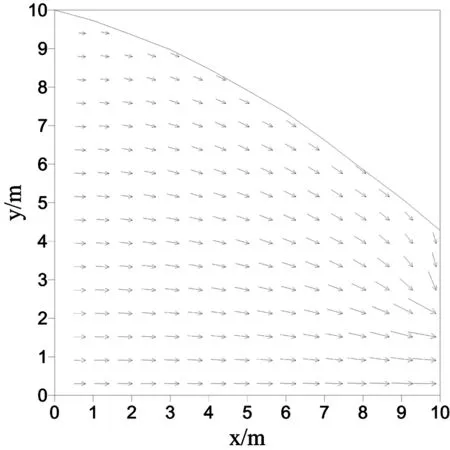
图3 流速矢量图

图4 水头等值线图
2.2 算例二
某沥青混凝土心墙砂砾石坝,坝高72m,顶宽8m,上游坝坡为1∶2.35,下游坝坡为1∶2.15,上游正常蓄水位为213m,下游按无水考虑。坝址处坝基覆盖层深150m左右,共分四层:Ⅰ砂卵砾石层;Ⅱ砂层;Ⅲ含漂块碎石层;Ⅳ含块卵砾石层。大坝简化计算模型如图5所示,覆盖层渗透系数见表2所示[5]。坝体心墙为不透水防渗体,文章仅对坝基覆盖层进行渗流分析,共剖分三角形单元1552个,结点854个[6]。
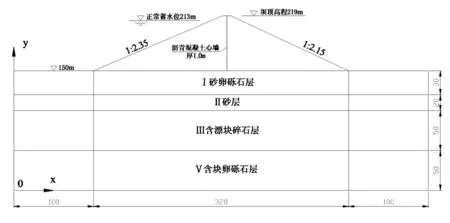
图5 模型简化图

图6 有限元网格图

表2 覆盖层各层渗透系数
坝基覆盖层未作任何防渗及排渗措施的情况下,计算得到渗流场水头分布如图7所示,流速矢量分布如图8所示。

图7 水头等值线图

图8 流速矢量图
计算结果分析:从图7可看出,上游坝踵及下游坝趾附近水头等值线较密集,说明此两处覆盖层地基的水力坡降较大,计算的最大水力坡降值为0.7,此值已经超过了该地基土的允许水力坡降0.1。图3-8也显示出上游坝踵及下游坝趾附近渗流流速比较大。在无防渗措施下的坝基覆盖层的单宽流量为6.35×10-3m3/(s·m),单宽流量的计算结果合理。以上计算结果说明,深厚覆盖层地基是一种强透水地层,需作相应的防渗及排渗措施。
3 结 论
主要论述求解深厚覆盖层地基渗流场的二维有限元方法,开发相应的计算程序,利用常规三角形单元计算坝基渗流场。通过算例对比分析,程序设计合理,求解结果一致,精度相对较高。综合认为深厚覆盖层地基是一种强透水性地基,若不作相应的排渗排水措施,将会影响大坝安全和工程效益。

