基于时间序列模型的边坡位移预测研究

张恒言

(广东河海工程咨询有限公司，广州 510610)

0 引 言

边坡在发生滑动前均会产生一定的变形，边坡变形监测的意义在于能够在边坡完全破坏前反馈预报预警信息，从而实现防灾减灾[1]。随着计算机和智能科学的发展，人工智能预测滑坡已然成为岩土工程领域重要的研究分析手段。常用的人工智能预测法包括：灰色预测模型、时间序列预测模型神经网络等方法[2-8]。其中时间序列方法分析是基于已有的观测序列数据随机机制及对序列为例的可能发展趋势进行预测的一个重要方法，目前已经广泛用于滑坡预测、基坑桥梁变形预测等多个方面。差分自回归移动平均模型(ARIMA)是一种时间序列典型预测算法，常用于对滑坡未来变形情况进行预测[9]。

1 边坡位移预测模型介绍

ARIMA-整合移动平均自回归模型是时间序列预测分析方法之一。ARIMA时间序列预测模型在基于差分算法的基础上，将非平稳时间序列转化为平稳时间序列，进一步将因变量对于自变量的滞后性及随机误差项进行回归分析的一种模型方法。具体表达式为：

yi=△dφi=(1-L)φi

(1)

yi=Φ1yi-1+Φ2yi-2+…+Φpyi-p+
ε-β1εt-1-β2εt-2-…-βpεt-p

(2)

式中：非平稳时间序列用φt进行表示；经过差分后得到的平稳序列为yi；yt为时间序列y的当前值；Φ1，…Φp是自回归系数；p是自回归阶数；βp是移动平均系数；q是移动平均阶数；[εt]是白噪声序列。

2 边坡概况

2.1 工程概况

某填土边坡，坡脚为种植区，边坡长度约304m，坡顶设计高程417-421m，坡脚设计高程388-408m。边坡为永久性边坡，工程重要性等级为一级，重要性系数取值为1.1。边坡防护结构综合采用加筋挡土墙与扶壁式混凝土挡墙及桩基托梁的进行支护，见图1。

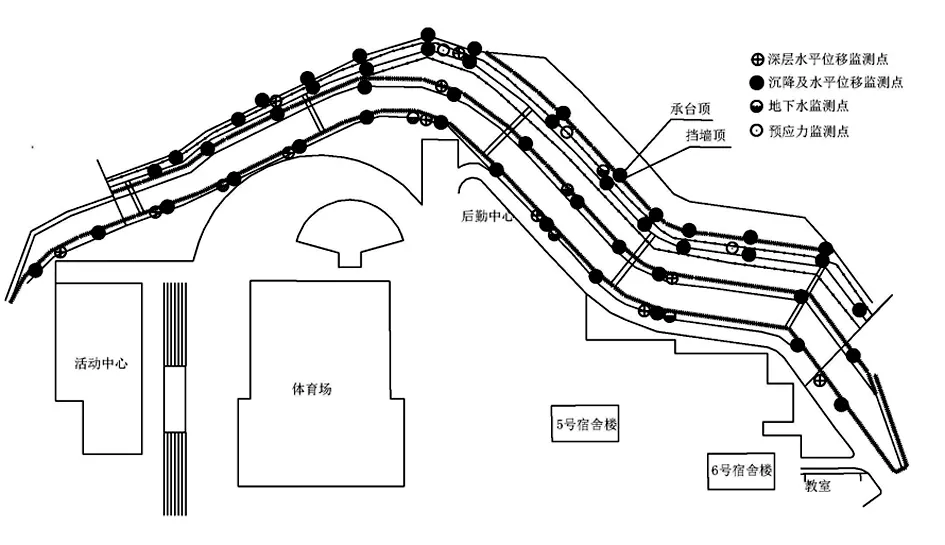
图1 研究区边坡监测点平面布置图

2.2 地层岩性

研究区为低山坡麓地貌单元，整体东南高其余低，整体坡度约30°-50°，场地土层自上而下划分为：

1)素填土：该层土土质不均匀，厚度介于1-6.3m，平均厚度3.6m，颜色为褐黄色，稍密。主要成因为坡体开挖时的全、强风化岩。

2)粉质黏土：揭露厚度介于0.7-4.5m，平均厚度2.4m。颜色为褐黄色，可塑-硬塑状，砂粒含量大约为10%左右。

3)全风化花岗岩：揭露厚度2.3 -6.0m，平均厚度为5.6m，颜色为褐黄色，岩体质量极软，极破碎，质量等级为Ⅴ级。

4)砂土状强风化辉绿岩：分化程度较高，颜色褐黄，岩体质量极软，极破碎，岩体基本质量等级为Ⅴ类。

5)砂砾状强风化花岗岩：钻孔揭露厚度1.12-19.7m，平均厚度6.9m。颜色灰黄、灰白色，散体状。岩体坚硬程度为极软岩，极破碎。

6)碎块状强风化花岗岩：分化程度较高，灰黄色，碎裂结构，岩体基本质量等级为Ⅴ类。

3 基于时间序列的边坡位移预测

数据源自边坡2019年12月—2021年2月共77次的水平位移监测数据，汇总结果见图2。结果表明，在2020年2月时边坡位移迅速增大，其值为85mm，这主要是由于边坡开挖导致的，这一结果表明，边坡开挖对边坡稳定性影响较大。随后在开挖段修建挡土墙，防护工程修建完成后，可以看到位移量增长较慢，但由于后期填筑高度增加，坡顶水平位移又开始产生较大的增量。总体结果表明，该边坡处于不稳定状态。为了对边坡为来的发展趋势进行预测及预警，有必要建立模型对坡顶位移进行分析，为该边坡的稳定性分析提供理论依据[10-11]。

图2 边坡S5监测点水平位移曲线图

3.1 ARIMA模型建立

基于上文式1与2的分析可知，建立模型时需知道d阶数、自回归阶数和移动平均数。文章给出了具体的建模流程。具体建模过程见图3。

图3 ARIMA建模流程

通常，滑坡的发生时内外多种因素共同耦合作用下导致的一种非线性过程，因此滑坡实时位移监测数据属于非线性非平稳数列，为了获取平稳数列，本模型中的参数d由差分的阶数来确定。当确定d以后还需要对获得的数列进行平稳性检验。常采用单位根检验方法。常用的类型有PP检验、ADF检验以及NP检验等。文章采用ADF检验法。

基于原始监测数据，得到一阶和二阶查差分曲线见图4。结果表明，在一阶差分时数列即可保持平稳。同时采用ADF检验得导ADF值为-5.34，远远小于显著水平为5%的临界值。基于以上分析确定d=1.0。自回归阶数可以通过自相关函数确定，移动平均阶数可通过偏自相关函数确定。判断准则如表1所示。其中自相关函数式表示为：

(a)一阶差分 (b)二阶差分图4 边坡水平位移差分结果

表1 模型p和q判断准则

(3)

式中：k为滞后期数；yi为期望值。

偏自相关函数描述的是给定中值下，预期值与观测值之间的相关性。根据图5，当一阶差分曲线的ACF函数在一阶以后序列很平稳并逐渐趋于0，因此确定p=1.0，q=1.0。

(a)自相关函数

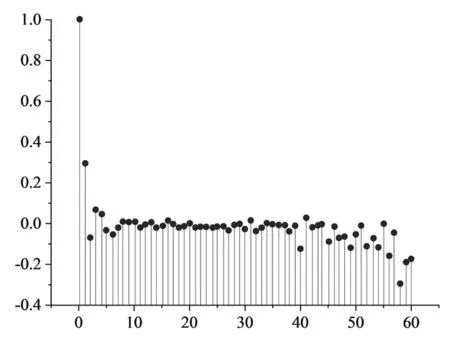
(b)偏自相关函数图5 自相关函数与偏自相关函数图

通常自回归阶数，移动平均阶数，可能会发生主观性选择失误，进而导致选错参数，引起模型失真。文章综合采用贝叶斯信息准则(BIC)判断模型阶数，其计算公式为：

BIC=kIn(n)-2In(L)

(4)

式中：k为模型参数个数；n为样本数；L为似然函数。

图6为基于式(4)得到的时序位移BIC图。图6表示，颜色越低代表BIC值越低。结合图5当AR为1.0、MA为1.0时，BIC值最小。综合以上判断，在文章建立的ARIMA模型中选择自回归阶数为1.0和移动平均阶数为1.0是合理的。

图6 时序位移BIC图

3.2 边坡位移预测

根据以上分析，选取参数分别为d阶数为1，自回归阶数p为1，移动平均阶数q为1，最终建立ARIMA(1,1,1)模型见图7。结果表明，原始曲线和预测曲线高度吻合，证明模型的有效性。此外，根据预测，未来一段时间内，边坡位移很小能够保持稳定，结合实际数据，符合边坡发展趋势。

图7 S5监测点位移预测图

3.3 结果分析

前文已经验证了模型的合理性，为了得到更为理想的预测结果，又进行了进一步验证，利用文章提出的模型，建立S1和S2监测点坡顶水平位移时序曲线得到图8，并与实际数据进行对比分析。注意的是，由于数据过多，文章选择了前十次数据作为建模数据。结果表明，S1、S2监测点坡顶水平位移的变化过程与前文的S5基本一致。根据图8中的S1、S2结果可以看出，S1和S2的位移先增长后保持稳定，S1最大位移增加至61mm，S2最大位移增加至82mm，在支护结构完成后，位移变化有所减缓。

图8 S1和S2监测点时序位移预测图

表2汇总得到了实时监测结果与文章模型分析得到的结果，可以看到，在2021年4月，S1监测点水平位移累计变化量为81.1mm，S2累计水平位移为99.3mm，二对应的文章模型计算结果分别为83.2 mm和98.3 mm，差值分别为-0.8mm和1mm。总体结果表明，实际结果与所采用的的ARIMA模型结果基本一致，证明文章的合理性。

表2 S1和S2监测数据与建模预测数据对比

4 结 论

1)建立了ARIMA模型，通过该模型对选矿厂滑坡2019年至2021年的坡顶位移进行建模，通过自相关函数、偏自相关函数以及BIC准则得到模型d阶数、自回归阶数和移动平均阶数参数取值方法。

2)利用ARIMA时间序列预测模型对研究区的边坡位移进行预测，并与实时监测数据进行对比分析，结果表明，模型结果与实时监测数据高度吻合，证明模型的有效性，并可利用该模型对边坡未来的发展趋势进行预测预警，及时采取防范措施。