变水头下管涌细颗粒迁移试验

陈 亮，滕耀宗，蔡国栋，尹子学，万 昱

(1.河海大学岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098;2.河海大学岩土工程研究所，江苏 南京 210098)

管涌作为汛期堤防危害性较大的一种破坏形式，一旦形成破坏将带来巨大的财产损失[1-2]。Ojha等[3-4]基于达西模型等经典理论，提出了确定临界水头的公式。随着技术的进步，各种试验模型不断更新，逐步由单层转向双层、三层以及多层堤基结构[5-8]。

近年来，根据各水文站监测结果，我国南方地区汛期雨水多、强度大，对堤防带来了不可忽视的损害。陈栋等[9]对2020年汛期各湖区堤岸险情进行分析，发现湖区发生管涌险情最为频繁，占65.9%。洪水过境的水位变化与稳定渗流不同，属于变水头范畴，已有学者在变水头方面开展了研究。陈亮等[10]研究了非稳定流下管涌发生和发展的规律；张嵩云等[11]采用有限元软件GeoStudio，通过渗流-稳定耦合模拟堤坝在洪水过程中的稳定性，为堤坝设计提供依据；倪小东等[12-13]采用颗粒流PFC模拟了非稳定流下管涌的发生和发展，模拟结果与实际工程相吻合；苏永军等[14]利用有限元结合分形理论，得到了各分维值随水头变化明显且与水位涨落成正比的规律。大坝安全运行至关重要，学者们基于不同理论建立了安全预测模型。吕鹏等[15]基于FDA，将离散指标数据转换为连续函数，建立了大坝安全动态评价模型；谷艳昌等[16]基于遗传算法，建立了GA-SVM大坝安全性态预测模型。

汛期洪水过境，水位短期内迅速上涨，洪峰后水位逐渐下降，同时洪水过境在一段时间内可能存在多次。因此为尽可能与实际工况相符，可将洪水过境的水位近似简化为正弦曲线变化形式[17-19]。张哲等[20]对土体在不同周期和振幅的正弦水头作用下的管涌特性规律进行了分析，但是未对细颗粒运动、迁出及渗流通道发展过程进行细观研究。为此，本文通过自下而上渗流的管涌装置，使用便于分层观察、追踪迁移的彩砂作为细颗粒，对不同细颗粒含量和不同孔隙比共8组试样在常水头和变水头下进行试验，探究变水头下土体内部细颗粒运动及迁出的规律。

1 间断级配无黏性土管涌试验

1.1 试验装置

试验采用自主研发的圆柱体管涌试验装置，该装置由供水系统、试验柱、数据收集系统、流失颗粒收集系统组成，如图1所示。供水系统由电机牵引绳子带动水箱上下移动；数据收集系统包括孔压传感器、流量计、无纸记录仪、信号转换器等；孔压传感器量程为0～15 kPa，精度为±0.2%FS，流量计量程为0～316 mL/s，精度为1%；无纸记录仪对孔压与流量数据进行记录和存储，只能接收电流或电压信号，因此需使用信号转换器将流量计输出的信号转换为4～20 mA电流信号；收集系统中天平量程为500 g，精度为0.01 g。

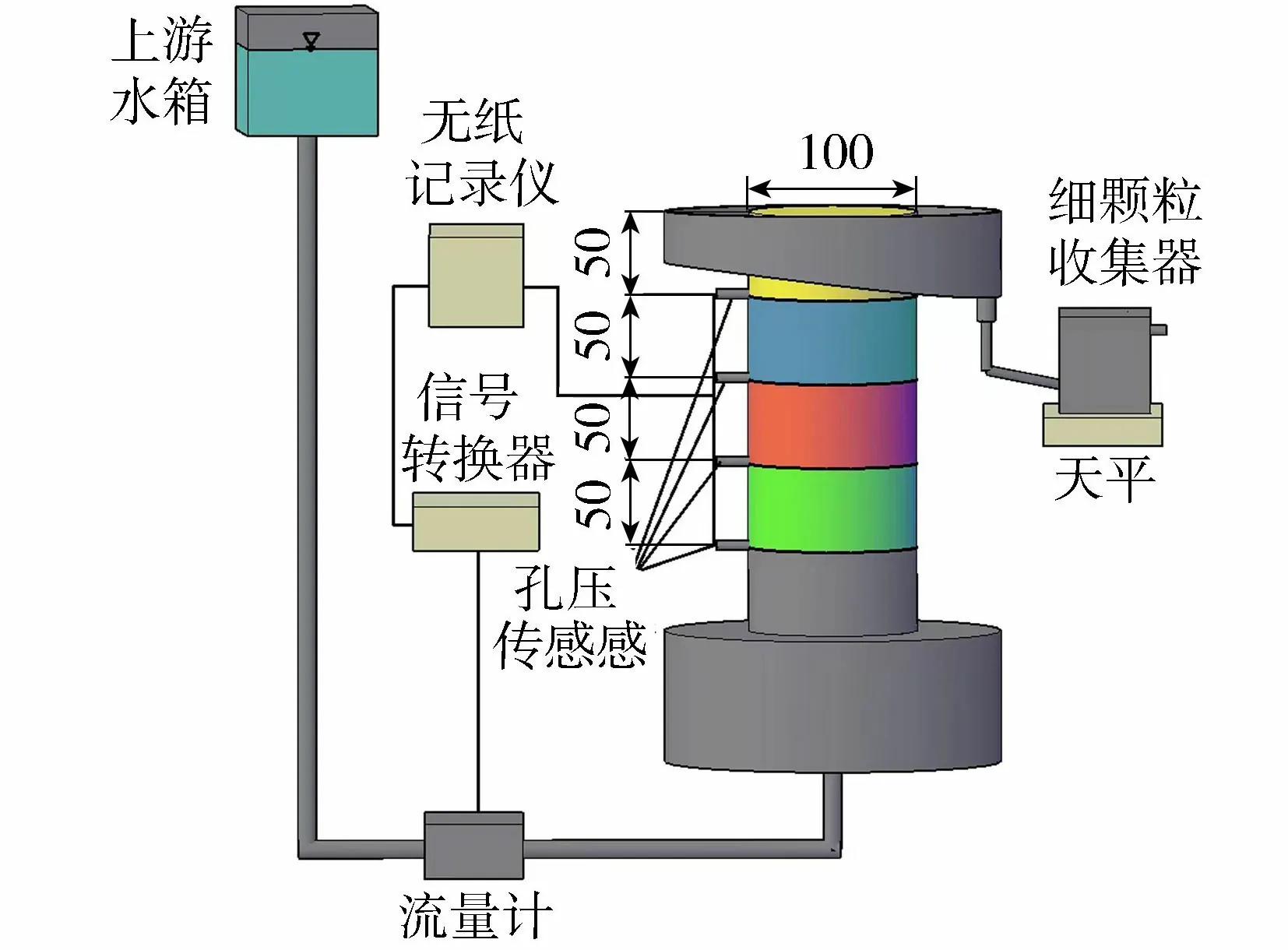
图1 试验装置构造 (单位：mm)Fig.1 Construction of test device (unit: mm)

1.2 试验材料与方案

试验材料为长江边河滩地区的砂土，采样地点位于南京市板桥汽渡。根据Kenny等[21]的渗透稳定性准则，试样中粗颗粒粒径为2～8 mm，其中2～4 mm占70%，4～8 mm占30%；细颗粒为粒径0.075～0.25 mm的细砂。细砂经水洗烘干后与染色剂(德国SINO-401石材染色剂[22])均匀拌合染色，染色风干后水中浸泡48 h未发现褪色现象。试样级配曲线及比重信息如图2所示，试验方案见表1。试验组Sin-FC与Sin-U-0.5试样用于研究不同细颗粒含量(质量分数，下同)下的规律，试验组Sin-U用于研究不同孔隙比下的规律，Con-U作为Sin-U的对照组。

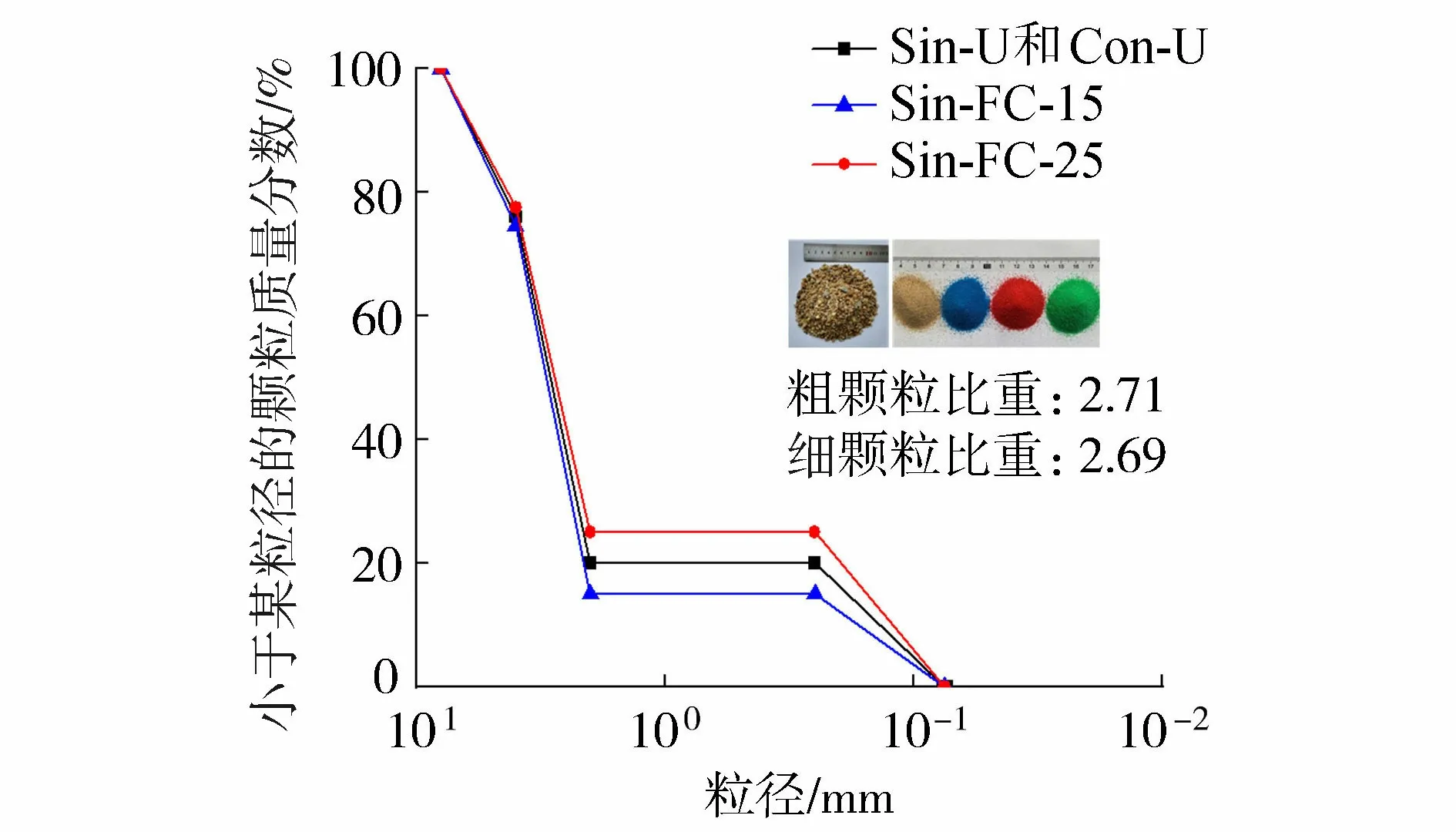
图2 试验用料级配曲线Fig.2 Gradation curve of test materials

表1 变水头试验方案

1.3 试验步骤

a.试验开始前需对数据采集系统进行标定。采用湿拌法将粗颗粒与细颗粒充分拌匀，每层厚度为50 mm，按照绿、红、蓝、黄颜色顺序由下至上分层击实装样。将外部水头固定，使液面和试样顶面齐平，试样饱和24 h以上。

b.从饱和时的水头高度开始，逐级提升上游水头，每级水头瞬时提升4 cm且维持4 min。待顶部有红或绿色细颗粒涌出时，维持4 min后开始降低水头，降低速率和水头维持时间与上升段一致，当降低至试样顶面不发生涌砂时，为一次循环。以上一次循环结束时的水头为起始点进行下一次的循环，水头循环共进行3次。最终使得水头变化的线形近似为正弦式，与水文站汛期水头变化相似。Con-U试验组与Sin-FC、Sin-U试验组第一次循环的上升段操作相同，Con-U组在达到峰值水头后将水头固定，直至与3次循环结束时间一致时结束试验。每级水头存在停留平台主要为了使各级水头对土体充分影响。

c.每一级水头下，记录出砂的颜色、出砂时水头位置、出砂时间并收集涌砂，通过天平读数计算细颗粒流失量。

2 试验结果与分析

2.1 迁移过程及管涌后迁移通道分析

不同工况细颗粒迁移有相似特征，选取Sin-U-0.4试样观察变水头下细颗粒迁出现象。初始阶段，试样在水头升高过程中保持稳定，细颗粒为静止状态；当水头提升到细颗粒启动时，细颗粒开始跳跃，试样表面在粗颗粒之间出现细小的管涌口，管涌口随水头的提高不断增多同时向四周扩张，迁移通道逐渐贯通，最终试样顶面出现红色或绿色细颗粒，迁移通道贯通。在水头下降阶段，管涌口细颗粒流失程度减缓，孔口堆积的细砂有向通道回流的现象，管涌口产生回缩。之后的水头循环中已有的管涌口扩展，同时产生新的管涌口。因此可将一次循环中细颗粒迁出分为4个阶段：稳定阶段、细颗粒位置调整阶段、细颗粒迁出阶段、细颗粒迁出减缓阶段。

试验结束后，从顶面每隔2.5 cm挖取土样并拍照，如图3所示，结合照片和数据分析各层细颗粒迁移情况。试样顶面有3种颜色颗粒，且从黄、蓝到红色的细颗粒含量依次递减。2.5 cm横截面处可明显观察到由于细颗粒大量的迁移而剩下粗颗粒骨架所形成的空洞，且空洞不止一个，即产生多条通道。中上部细颗粒迁出比下部多，从顶部到底部，迁移通道有效面积在逐渐变小，2.5 cm横截面的迁移通道面积占截面47.7%，5 cm横截面的迁移通道面积占19.9%，而中下部通道面积不足10%。由此可认为迁移通道由下游逐渐向上游扩展且沿着渗流方向在薄弱处曲折发展，通道截面多为不规则长椭圆形。在下部横截面中存在上层颜色的细颗粒，由此说明细颗粒存在逆流运动，在12.5 cm和17.5 cm横截面处可观察到此现象。

图3 Sin-U-0.4试样顶面及横截面Fig.3 Top surface and cross sections of Sin-U-0.4 sample

2.2 渗透系数与细颗粒运动分析

由图4可以看出，常水头下渗透系数随时间逐渐增大，而变水头下的渗透系数整体呈正弦上升趋势。细颗粒迁移过程中大量聚集于通道中，会引起堵塞，渗透系数降低，这种现象是随机的、短暂的，在管涌破坏中很常见，文献[23-24]中也存在此现象。在常水头和变水头上升段中，细颗粒在受到向上渗透力的作用下发生迁移从而渗透系数增大，即使向上迁移过程中偶尔会发生堵塞使得渗透系数短暂降低，但最终均会冲破堵塞后细颗粒继续迁移，这种颗粒迁移规律在文献[25]中也存在。

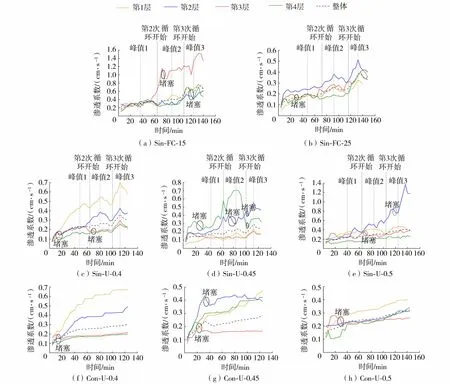
图4 各试样渗透系数随时间变化Fig.4 Variation of permeability coefficient over time of each sample

由试验现象可知，水头下降阶段细颗粒不断迁出土体，使试样孔隙比增大，根据柯森-卡门渗透系数公式，渗透系数应增加，但试样整体渗透系数随着外部水头的降低出现减小或者先增加再减小的现象(图4)。随着水头下降，水流开始无法支持通道内的全部细颗粒向上运动，所以部分细颗粒开始下落并在孔隙处聚集，与下部上涌的细颗粒一起堵塞孔隙，对下部细颗粒的迁移和水流的运动产生阻碍，因而渗透系数减小。因此细颗粒在下降段颗粒运动较紊乱，颗粒运动方向存在随机性，如图5所示。

图5 变水头各阶段细颗粒运动情况Fig.5 Movement of fine particles in each stage under the variable head condition

2.3 细颗粒迁出分析

由图6可知，累计流失量随着细颗粒含量的增加而增加，随着孔隙比的增加而减小。常水头下，累计流失量的增加逐渐变缓，最终在相同试验条件下总流失量小于变水头下的试样。常水头下，细颗粒在迁出过程中其所在位置不断发生变化，最终在恒定的水头下受力平衡保持稳定而不发生迁移。而变水头下，细颗粒累计流失量近似为直线增加，但在峰值水头两侧曲线的斜率明显上升段大于下降段，呈现略微的波动。由此说明一旦超过临界水力梯度，即使在水头下降的过程中，流失量也一直在增加，管涌依然会发生。水头下降阶段，通道中的细颗粒存在下沉现象，打破了在上升阶段具有的与常水头下类似的平衡状态，颗粒重新分布，且比试验前松散，同时上升段存在的堵塞现象会被打破，使得细颗粒在下一级循环中更容易迁出，因此累计流失量大于常水头下的流失量。

图6 细颗粒累计流失量随时间变化Fig.6 Variation of cumulative fine particle loss of specimen over time

随着水头循环次数的增加，细颗粒的累计流失量增大，土体的渗透系数也逐渐增加，这和细颗粒在粗颗粒骨架内运动和迁出土体是密不可分的。采用Boltzmann模型对Sin-FC、Sin-U与Con-U组细颗粒累计流失量ms进行拟合：

(1)

式中：t为时间；A1、A2、A3、t0为模型参数，具体取值见表2。

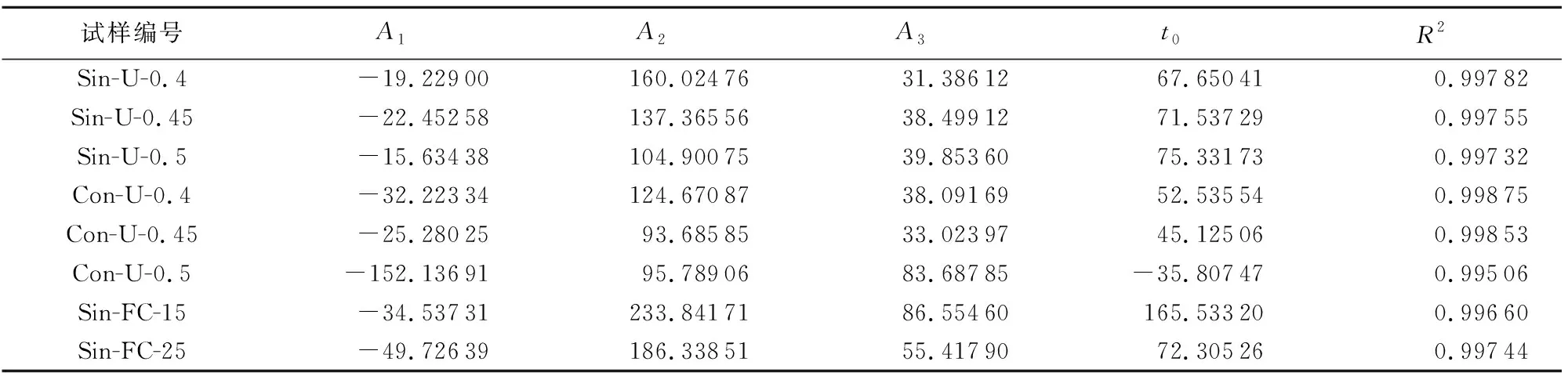
表2 细颗粒累计流失量模型参数取值

由拟合曲线可得，Boltzmann模型在常水头下的拟合效果要好于变水头。变水头下，水头上升与下降段颗粒流失速率不同，存在偏离拟合曲线趋势，但随着迁移通道的不断贯通，细颗粒流失更容易，在第3次循环时，细颗粒累计流失量可较好地分布于拟合曲线上,因此Boltzmann模型在变水头下拟合细颗粒累计流失量时也较为适用。

各层流失量为各层总的流失量与其他层的补给量之差。从图7可以看出，各试样流失量主要集中于下游，因此由于细颗粒迁移导致的空洞也多见于下游。在相同水力梯度条件下，下游较上游迁移通道短，更容易迁出。对比Sin-U组与Con-U组各层流失量，Sin-U组上半部分迁出量在55%至65%之间，Con-U组上半部分迁出量为69%以上，而Sin-U组的总迁出量大于Con-U组，即Sin-U组下半部分迁出较多，Sin-FC组中下半部分迁出量占40%左右，与上半部分迁出量相当，因此可以说明变水头使得迁移通道贯通范围更大，对土体结构破坏更严重。

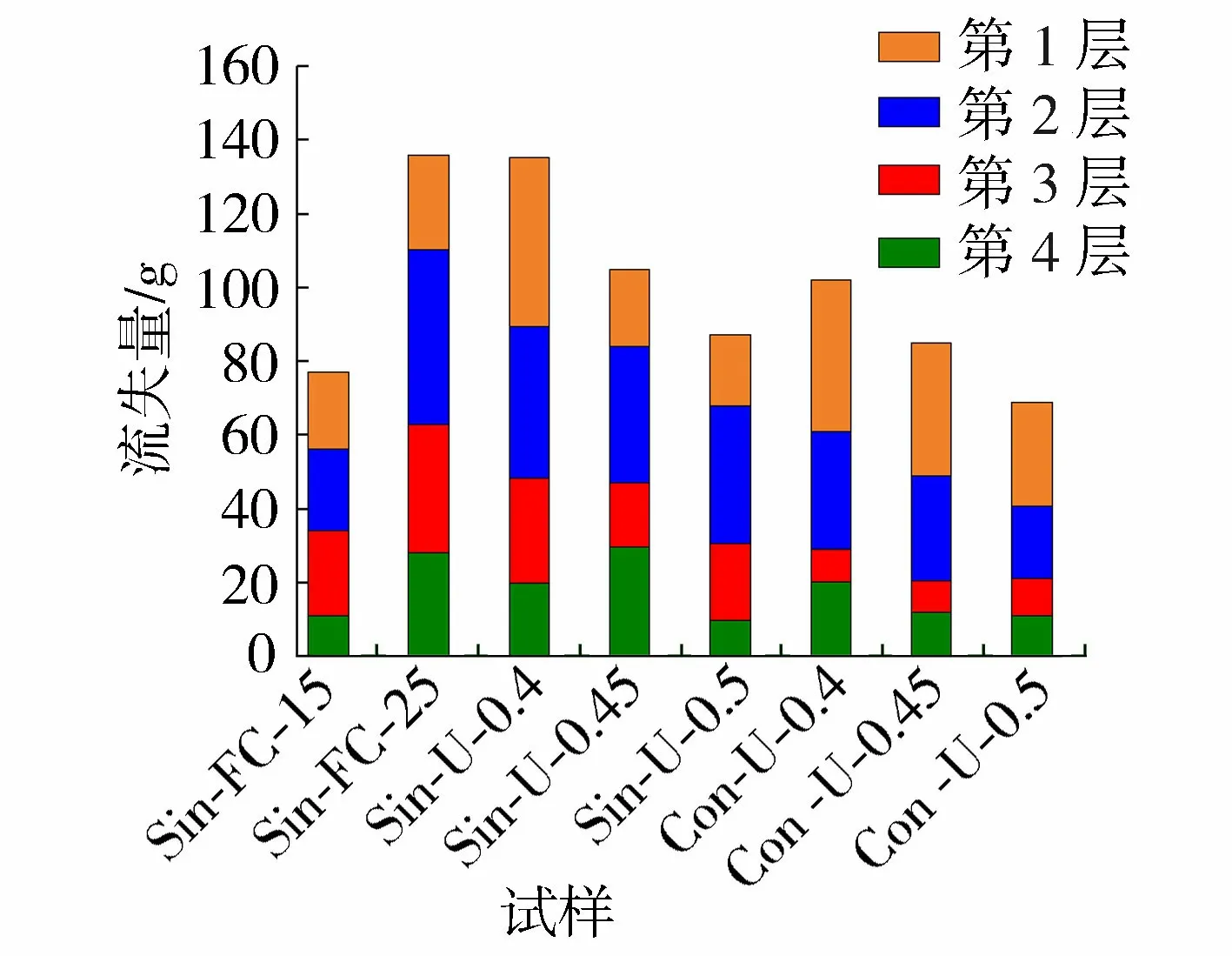
图7 各试样总流失量与各层流失量Fig.7 Total loss and loss of each layer of each sample

2.4 水力梯度变化规律分析

峰值水头为底部细颗粒迁移出土体时的破坏水头，将此时水头对应的水力梯度定义为破坏水力梯度。由图8可知，Con-U试验组中，在保持最高水头的过程中，水力梯度逐渐降低，但降低幅度小于变水头。第1次循环的破坏水力梯度随孔隙比的减小而增加，细颗粒含量为20%时最大。在逐次水头循环中，孔隙比越小的试样，破坏水力梯度减小幅度越大。主要由于孔隙比小的试样潜在迁移通道的部分占比较小，因而第1次循环需要较大的水力梯度才能发生管涌破坏，当土体迁移通道贯通后孔隙增大，底部细颗粒迁出所需要的水力梯度明显降低。细颗粒含量越大，破坏水力梯度降低的幅度越大。破坏水力梯度的降低幅度与细颗粒累计流失量和渗透系数变化紧密相关，降低幅度越大说明在之前水头循环过后流失量较大，使得渗透系数变大，细颗粒的迁移变得更为容易。各循环过程中的破坏水力梯度见表3。由表3结合流失量数据可得，细颗粒累计流失量与最大破坏水力梯度差呈正相关，降低幅度大说明内部细颗粒流失较多。因此，破坏水力梯度的变化幅度可作为评判土体内部细颗粒流失程度的一个指标。

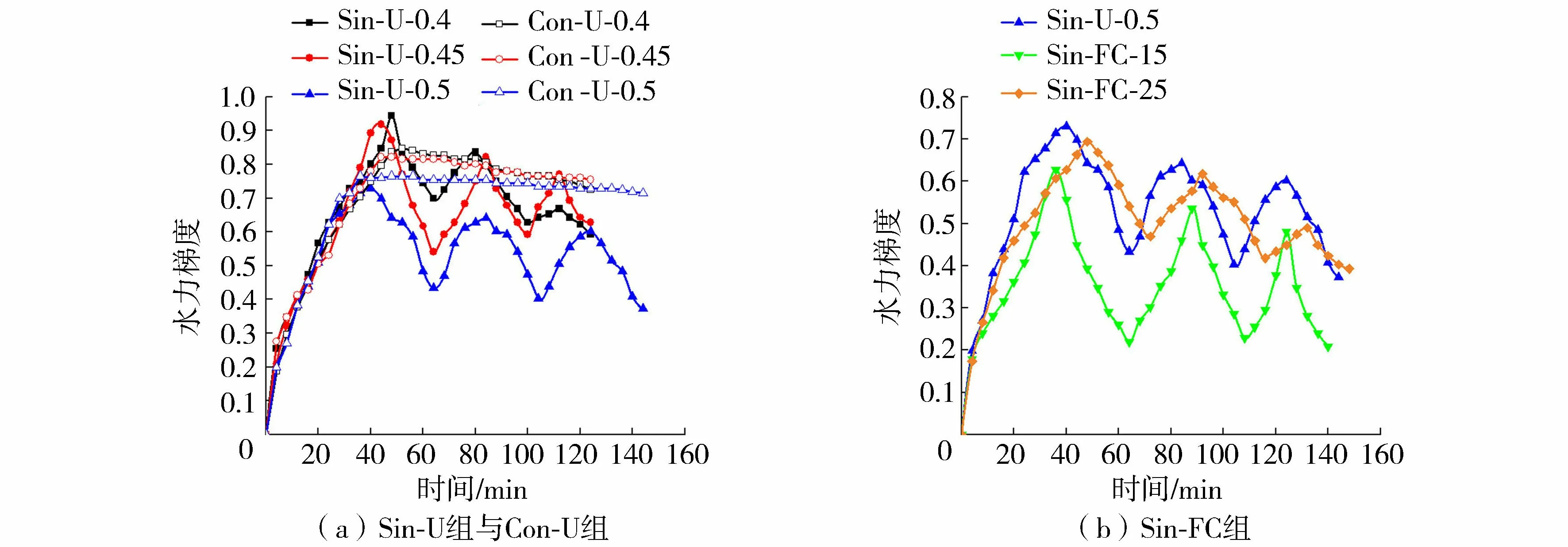
图8 水力梯度时程曲线Fig.8 Time series of hydraulic gradient of specimen

表3 各试样破坏水力梯度

3 结 论

a.变水头下渗透系数随时间的变化并不同于常水头下的持续增加，而是整体上呈正弦上升趋势，在迁移过程中无论水头上升还是下降均存在通道堵塞现象，下降段细颗粒存在由下游向上游逆水流运动的现象。

b.常水头下细颗粒累计流失量趋缓增加，而变水头近似直线增加且在水头上升和下降交界处有所波动流失主要集中在下游，通道截面有效面积从下游到上游逐渐变小，且变水头迁移通道贯通范围更大，二者使用Boltzmann模型进行拟合效果均较好；累计流失量与细颗粒含量呈正相关关系，与孔隙比呈负相关关系。

c.破坏水力梯度下降幅度可作为评判土体内部细颗粒流失程度的指标，常水头下破坏水力梯度的下降幅度明显小于变水头，反映了变水头细颗粒流失较常水头更为严重，细颗粒含量越大，孔隙比越小，破坏水力梯度下降幅度越大。