基于特征模型的电力系统在线动态等效建模

江叶峰，熊 浩，付 伟

(国网江苏省电力有限公司，江苏 南京 211100)

电力系统建模是电力系统运行分析与控制的基础和前提，对电力系统安全经济运行至关重要。现代电网的源、网、荷均发生了重大的变化，其结构和运行方式也愈发多样化，这对电力系统建模提出了新的要求。

传统电力系统建模一般采用离线方式。而对于现代电网，由于模型参数具有时变性，应在线采集数据并在线建模。传统电力系统建模一般采用集中方式，如省、网等各级调度中心统一建立全省、全网的模型。面向现代电网建模时，由于网络规模巨大，要对系统内所有元件同时建模几乎不可能。为此，可以利用电力系统的分层分区管理特点，采用分层分区建模方式[1]。分层建模时，对于某个层级的电网，除了要建立适用于自身需要的详细模型以外，还需要建立适用于上层电网的等效模型。如上层电网是220 kV及以上电压等级的输电网，下层电网是110 kV及以下电压等级的配电网，从输电网仿真计算的角度考虑，需要建立配电网的动态等效模型，再将其与输电网模型合并[2]，从而获得更为准确的全网模型。分区建模时，各级调度中心只建立自身的详细模型，而其他区域的电网通常采用等效模型。

现有的动态等效建模大多是基于研究系统内部元件机理模型的等效化简[3-5]，相对复杂且通用性不强。以负荷建模为例[6-7]，当负荷群中成分比较单一时，采用机理模型是合适的。当负荷群中的动态元件类型不止一种，或者虽然类型单一但特性相差较大时，就难以用单个等值机理去描述。若采用几种机理模型的组合，又会因为未知等值参数的增多而造成参数估计困难。

与此同时，针对工程对象结构复杂、精确的动力学建模越来越困难的情况，有学者在20世纪90年代提出了特征建模[8-12]的思想，并在航天工程中得到了成功应用[13]。特征模型与高阶系统的降阶模型不同，它将高阶模型的相关信息均压缩于几个特征参量中，但并不丢失信息，且模型结构简单、工程实现容易。此外，与以往的电力系统非机理模型不同，特征模型的特征参数是慢时变的，而现代电网的关键特征之一就是参数的时变性[14]。因此在进行电力系统在线等效建模时可以考虑采用特征建模方法。

本文针对现有基于元件机理进行动态等效建模可能导致模型结构复杂及参数辨识难度大的问题，引入模型结构简单、工程实现容易的特征建模方法，对下层电网进行在线实时等效建模，有效平衡等效模型简洁度与精确度之间的矛盾。

1 特征建模的原理

对于满足一定条件的非线性系统，在满足一定采样周期Δt的条件下，其等效特征模型[15]可以用一个二阶时变差分方程来描述：

x(k+1)=f1(k)x(k)+f2(k)x(k-1)+g1(k)u(k)+g2(k)u(k-1)

(1)

式中：x为状态量；u为控制量；k为时步；f1、f2、g1、g2分别为慢时变的系统参数。

对于式(1)，若短时间内认为特征模型参数基本不发生变化，可以采用最小二乘算法辨识；而对于参数时变的情况，可以采用递推最小二乘算法在线辨识时变参数[16]。

2 电网的特征建模方法

2.1 特征模型输入、输出变量的选择

当对下层电网进行动态等效建模时，特征模型的输入变量可以为母线电压幅值，或既考虑电压幅值又考虑电压相位，而输出变量为系统吸收的有功功率和无功功率，或电流实部和虚部。

2.1.1 特征模型的输入变量

对于下层电网特征模型的输入变量是否考虑电压相位，可以建立以下3种模型(以二阶模型为例)。

a.PQ-U模型。只考虑电压幅值为输入变量，不考虑电压相位，输出变量为功率：

(2)

b.PQ-Uφ模型。以电压幅值和相位作为输入变量，输出变量为功率：

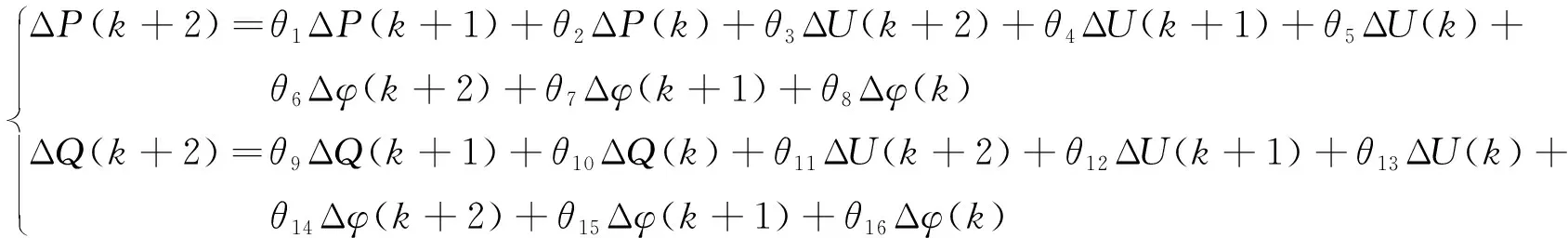
(3)

c.PQ-uduq模型。以电压直轴分量ud和电压交轴分量uq作为输入变量，输出变量为功率：

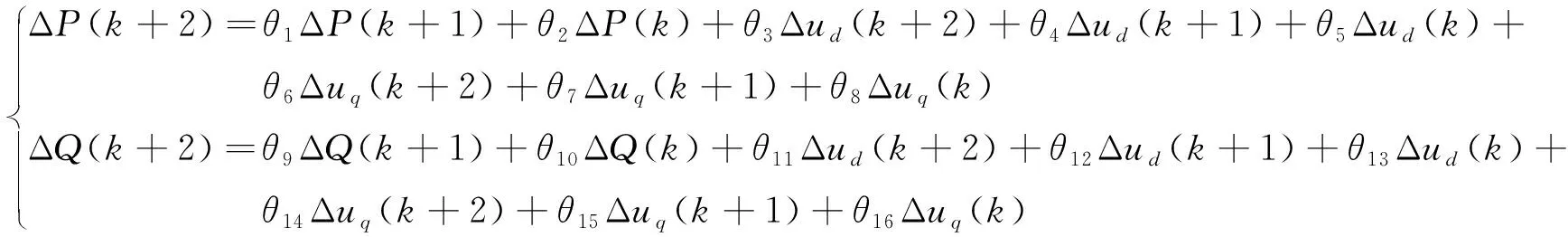
(4)

2.1.2 特征模型的输出变量

下层电网中主要的动态元件为发电机和负荷。

a.发电机元件[17]。设d、q轴各有一个等效阻尼绕组，可列出d轴和q轴的运算方程式：

ψd=G(s)uf-Xd(s)idψq=-Xq(s)iq

(5)

式中：G(s)为运算电导；Xd(s)、Xq(s)分别为d轴及q轴运算电抗；ψd、ψq分别为d轴及q轴磁链；id、iq分别为d轴及q轴电流；uf为励磁电压；s为拉普拉斯算子。

在稳态平衡点附近对发电机Park方程进行线性化，忽略较小项，此时转速接近1，进一步忽略定子电阻的影响，可得频域形式的方程为

ΔUd(s)=-Δψq(s) ΔUq(s)=Δψd(s)

(6)

式中：ΔUd、ΔUq分别为d轴及q轴电压增量；Δψq、Δψd分别为d轴及q轴磁链增量。

当维持励磁电压不变时，ΔUf(s)=0，由式(5)、式(6)可得：

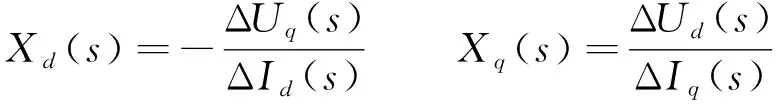
(7)

式中ΔId、ΔIq分别为d轴及q轴电流增量。

b.负荷元件[17]，主要包含电动机负荷和静态负荷。电动机负荷在频率及转速恒定的近似条件下，电流的状态方程本身是线性的，经过拉普拉斯变换可得输入电压和输出电流的线性关系式：

(8)

(9)

式中各变量的含义见文献[17]。

对于综合电动机模型(CLM模型)，还要加上静态负荷，令其导纳值为Gs+jBs，则综合负荷的总电流与电压之间的传递函数为

(10)

综上所述，无论对于发电机元件还是负荷元件，以电流分量作为输出变量的模型在合理假设之下是线性的，而以功率作为输出变量的模型是非线性的。本文所用的特征模型为线性的差分方程模型，因此理论上采用电流作为特征模型的输出变量时，应当比功率作为输出变量更合理。

为了对比功率和电流分别作为特征模型输出变量的效果，建立两种模型进行对比：①PQ-U模型，输入变量为电压，输出变量为功率，见式(2)。②IrIj-U模型，输入变量为电压，输出变量为电流，特征方程为

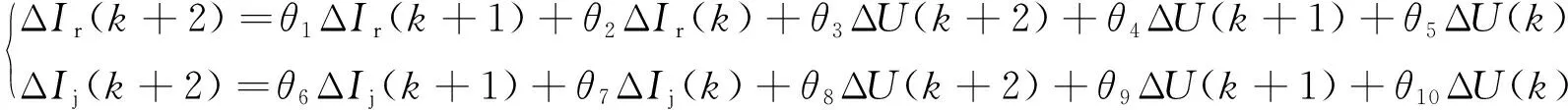
(11)

2.2 特征模型输入、输出变量的对比

以CEPRI-36节点系统为例，对比确定特征模型的输入、输出变量。仿真系统见文献[18]，假设下层电网由两个负荷以及一台发电机组成，BUS18负荷使用综合负荷模型，电动机比例为30%，静态负荷部分采用恒阻抗模型，BUS50负荷使用感应电动机模型，BUS5发电机采用5阶模型。

2.2.1 特征模型的输入变量对比

在外部电网施加扰动：1 s时，BUS16-BUS29线路BUS16一侧设置单相短路接地故障，接地阻抗为0.3+j3，0.2 s后切除。利用PSASP软件仿真记录下层电网的输入电压、总的有功功率以及无功功率。下层电网的输入电压幅值和相位变化如图1所示。

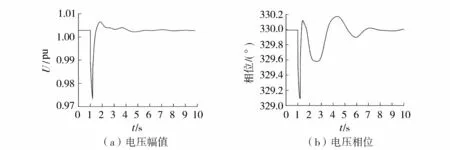
图1 下层电网的输入量Fig.1 Inputs of lower-level grid

采用最小二乘算法分别对PQ-U模型、PQ-Uφ模型和PQ-uduq模型的参数进行辨识，并用辨识的参数进行功率拟合，参数辨识结果如表1所示，功率拟合结果如图2所示。

表1 PQ-U模型、PQ-Uφ模型、PQ-uduq模型参数辨识结果

图2 特征模型的动态响应Fig.2 Dynamic responses of characteristic model

表2 3种模型的拟合误差对比

为了定量分析建模误差，采用均方根误差指标(RMSE)判断拟合效果。PQ-U模型、PQ-Uφ模型和PQ-uduq模型的误差对比如表2所示。从图2和表2可以看出，3种模型都能较好拟合下层电网的动态响应，误差都较小。PQ-Uφ模型和PQ-uduq模型的误差基本相当，PQ-U模型误差比PQ-Uφ模型和PQ-uduq模型稍大一点，但也很小。由此可见，忽略相位后的特征模型对功率拟合影响不是很大。因此，后续对于特征模型的分析中不再将电压相位作为输入，而只考虑将电压幅值作为输入。

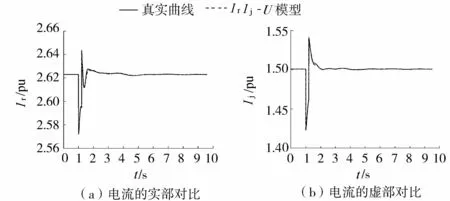
图3 IrIj-U模型的动态响应Fig.3 Dynamic responses of IrIj-U model

2.2.2 特征模型的输出变量对比

根据算例，对比PQ-U模型和IrIj-U模型在3%、5%、10%、15%、20%和30%6种不同扰动电压跌落程度下(单相短路接地，调整短路接地阻抗使得电压跌落程度不同)模型的适应性。

以扰动1为例，电压输入见图1(a)，扰动1下PQ-U模型的功率拟合见图2，IrIj-U模型的电流拟合见图3。

不同扰动电压下PQ-U模型和IrIj-U模型计算出的有功功率P、无功功率Q、电流实部Ir以及电流虚部Ij的拟合误差对比见表3。从图2、图3和表3可见，PQ-U模型、IrIj-U模型都能较好拟合下层电网的功率和电流，误差均较小。总体来说，PQ-U模型和IrIj-U模型的拟合误差基本相当，IrIj-U模型拟合误差小一点。

表3 PQ-U模型和IrIj-U模型的拟合误差对比

不同扰动下PQ-U模型和IrIj-U模型的参数辨识结果见表4。以扰动1下辨识的参数为准确参数，计算其他扰动下参数的误差百分比，见表5。

表4 PQ-U模型和IrIj-U模型的辨识参数

表5 PQ-U模型和IrIj-U模型其他扰动下参数与扰动1参数的误差百分比

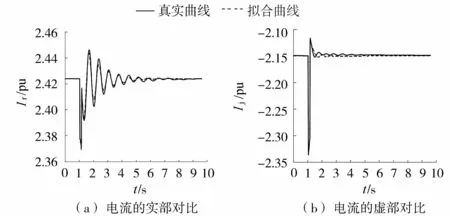
图4 实际电网IrIj-U模型的动态响应Fig.4 Dynamic responses of IrIj-U models in real power grid

由表2～5可以看出：①PQ-U模型和IrIj-U模型发生扰动电压跌落10%以下时，参数均基本保持平稳，变化不大，小扰动下PQ-U模型和IrIj-U模型都是适合的；②电压跌落达到15%及以上时，PQ-U模型和IrIj-U模型参数都发生了较大变化，因为机理模型是高阶系统，大扰动下采用低阶线性系统拟合，参数会发生较大变化；③总体来说，IrIj-U模型的参数平稳性要明显优于PQ-U模型。

综合考虑拟合效果、误差以及参数平稳性，以电压作为特征模型的输入量，电流实部和虚部作为特征模型的输出量，关于特征模型的分析都采用IrIj-U模型。

为了进一步验证特征建模的有效性，基于华中电网典型运行方式，采用特征模型对其中某一小区域进行等效建模。1 s时，节点A和B之间设置三相短路故障，接地阻抗0.03+j0.3，0.2 s后故障切除。IrIj-U模型与详细模型动态响应对比如图4所示，Ir的RMSE误差为1.499×10-3，Ij的RMSE误差为2.592×10-3，参数辨识结果为θ1=1.93，θ2=-0.96，θ3=1.77，θ4=-3.57，θ5=1.93，θ6=1.41，θ7=-0.48，θ8=18.60，θ9=-27.24，θ10=9.38。

3 特征模型参数的慢时变分析

前文对模型聚合方法的研究都是基于定常系数特征模型的分析，实际电力系统通常是慢时变的，相应特征模型的参数也应当是慢时变的。在电力系统机理模型参数发生变化时，研究其等效的非机理模型参数的变化情况，对参数慢时变特性进行分析。

以CEPRI-36节点系统为例，为研究其下层电网机理模型随时间缓慢变化时，对应特征模型参数的变化情况，按照如下方法仿真：采用下层电网中负荷18为综合负荷模型，其电动机比例是随时间变化的，总的仿真时间为20 s，以2 s为一个仿真时段，共分为10个仿真时段，每经过一个仿真时段，负荷的电动机比例增加3%，初始电动机比例为30%，最后一个仿真时段电动机比例为57%，具体变化如图5所示。为了能够在每个时段都能辨识出下层电网对应的特征模型参数，需要在每个时段开始时设置扰动。在BUS16处有一个静止无功补偿器，容量Qc=1 pu。仿真中，第一个时段开始时(0 s)切除此静止无功补偿器，第二个时段(2 s)再次投入静止无功补偿器，第三个时段(4 s)再次切除此静止无功补偿器，依此类推，不断交替切除或投入静止无功补偿器。根据仿真记录的电压及电流数据，采用递推最小二乘算法辨识下层电网特征模型的时变参数，参数初始值根据最初10个数据按最小二乘算法获取，具体参数变化如图6所示。

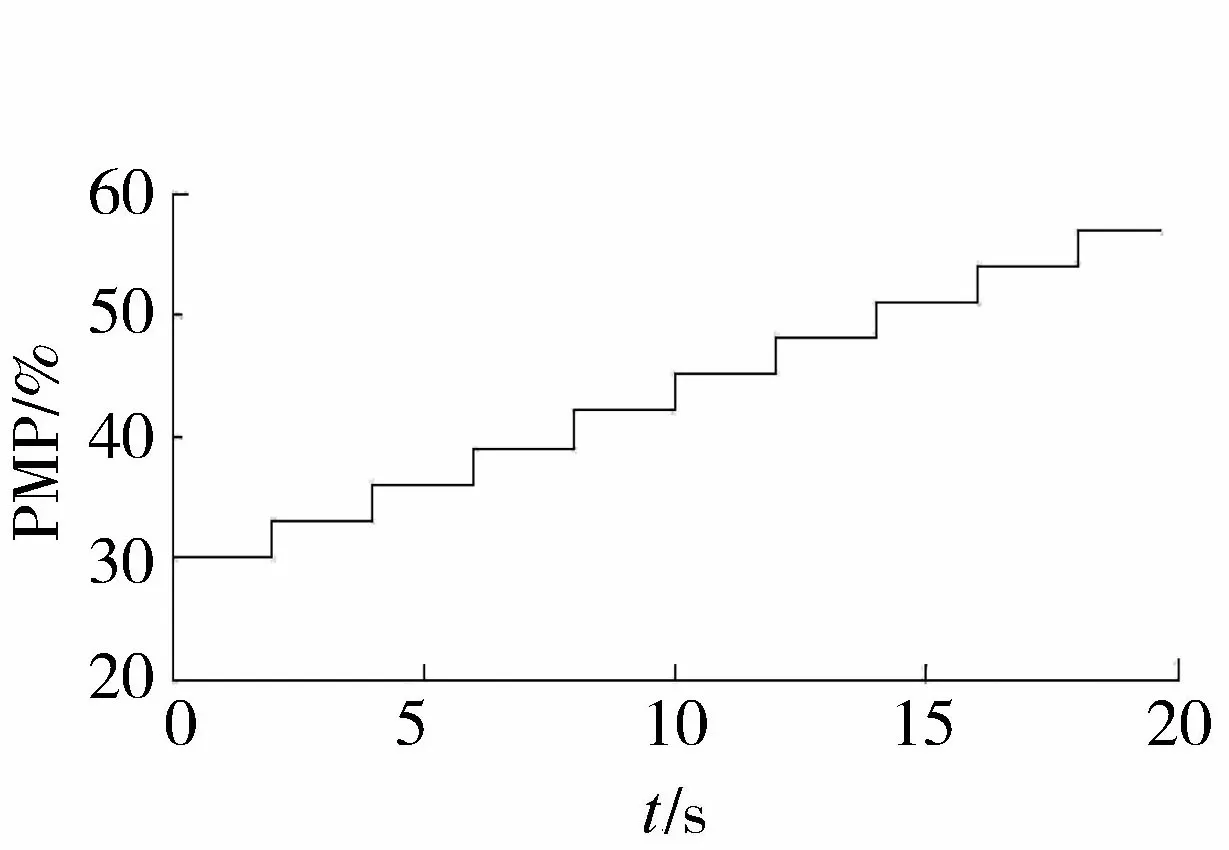
图5 负荷的电动机比例Fig.5 Motor-rate of load

图6 特征模型的动态响应Fig.6 Dynamic responses of characteristic model

由图6可以看出，由于扰动是在每个时段开始时施加的，扰动后特征模型参数会发生变化，每个时段结束时，特征模型参数基本能收敛下来(见图中的*点)。随着负荷的电动机比例发生变化，每个时段特征模型的收敛参数也会相应发生变化。电动机比例缓慢上升，θ2、θ3、θ5、θ7及θ8参数也随之缓慢上升。其中，θ2变化范围为[-0.808，-0.687 6]，最大变化率为17.901%，θ3变化范围为[3.747，4.57]，最大变化率为21.964%，θ5变化范围为[3.423，3.791]，最大变化率为10.751%，θ7变化范围为[-0.693 4，-0.346 9]，最大变化率为49.971%，θ8变化范围为[5.605，8.132]，最大变化率为45.085%。可见，θ7与θ8变化较大。θ1、θ4、θ6、θ9及θ10随之缓慢下降。θ1变化范围为[1.631，1.776]，最大变化率为8.164%，θ4变化范围为[-7.134， -8.357]，最大变化率为17.143%，θ6变化范围为[1.66，1.26]，最大变化率为24.096%，θ9变化范围为[-9.965， -11.26]，最大变化率为12.995%，θ10变化范围为[4.382，3.142]，最大变化率为28.298%。可见，θ6与θ10变化较大。由于电动机比例变化比较小，特征模型参数总体来说变化也比较小，对于慢时变的参数可采用递推最小二乘算法较好地辨识出来。

利用每个时段的收敛参数拟合每个时段的电流曲线，与仿真测量的功率曲线对比，如图7所示。

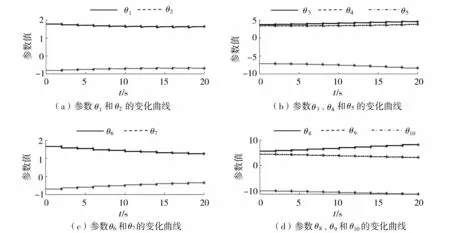
图7 特征模型的慢时变参数Fig.7 Slowly-time-varying parameters of characteristic model

结合图6、图7可以看出，由于机理模型发生变化，下层电网的输出电流实部和虚部曲线在不同时段发生了变化，因此对应的特征模型参数也逐渐变化。

4 结 语

本文引入模型结构简单、工程实现容易的特征建模方法，对下层或区域电网进行在线等效建模，有效平衡等效模型精确度和简洁度之间的矛盾。介绍了特征模型的结构及其参数辨识的算法，通过理论分析和仿真对比，选择电压为特征模型的输入变量，电流分量作为特征模型的输出变量，这种模型结构拟合误差小且参数平稳性高。实际负荷算例验证表明，特征模型可以较好地拟合下层电网的动态响应。对于参数的慢时变进行了简单的定性分析，分析了负荷机理模型发生的变化，当电动机比例改变时，相应的特征模型也会慢时变。