基于阿秒光电子谱研究金属光电子色散关系

潘子萌，刘 凯，马子琦，廖 青

武汉工程大学光电信息与能源工程学院，湖北 武汉 430205

强场物理是过去二十多年兴起的前沿学科，主要研究超强超短激光与物质相互作用。随着激光器的发展与进步，激光的脉冲宽度逐渐变窄，激光脉冲的功率越来越大［1-3］。利用先进激光技术获得的超快强激光脉冲与物质相互作用，成为了研究物质基本性质的一种重要手段。

阿秒物理学（1as = 1× 10-18s）研究飞秒和亚飞秒时间尺度上的超短激光脉冲与原子分子或固体相互作用时发生的电子动力学超快现象。强激光场聚焦在气体或固体介质上会产生高次谐波，高次谐波是一种非微扰的高阶非线性过程［4-8］。结合精确可控制的近红外（near-infrared，NIR）场，由高次谐波转换的极紫外（extreme-ultraviolet，XUV）阿秒脉冲已成功用于研究物质中电子的动力学过程。具体的技术思路是：XUV 阿秒脉冲和NIR 脉冲分别作为泵浦光和探测光，在精确控制两种激光脉冲之间的相对延时后共同与物质相互作用，通过观测阿秒光电子谱图以实现对电子运动的实时探测。近十多年来，阿秒光电子谱技术已被广泛应用于研究固体与原子目标中的时间分辨光电子发射［9］。

在激光与固体相互作用的过程中，束缚态电子在吸收光子后从固体表面出射，通常利用经典输运模型来解释从阿秒光电子谱图中提取的光电子发射时间。2015 年瑞士U.Keller 研究组开展了基于能量依赖的Ag（111）和Au（111）金属表面发射时间的研究，利用XUV 阿秒脉冲泵浦- NIR 激光脉冲探测技术首次观测到凝聚态系统中的亚周期动力学。他们的研究揭示了Ag（111）表面4d 能带和Au（111）表面5d 能带的发射时间极端依赖于光电子能量，与经典输运模型的预测大不相同［10］。最近的理论研究发现光电子发射时间依赖于固体中的能量色散关系，并揭示了固体中光电子输运时间与可观测到的光电子发射时间之间的尺度关系。通过光电子发射时间追溯到光电子在固体中积累的相位差，并且预测到负的光电子发射时间。基于上述发现，给出了一种时域的能量-动量-色散成像方法［11］。但由于研究中的模型势采用了均匀场，并不是真实金属内部势能，因此需要对模型势进行修正以便深入研究固体中的能量色散关系。

本文构建了非局域势为周期性势阱的单晶金属表面模型，用于近似真实的金属内部势能。改变XUV 阿秒脉冲和NIR 脉冲之间的相对延时，通过量子力学数值模拟计算得到了阿秒光电子谱图。发现光电子发射时间取决于势阱深度和穿越金属厚度，并且光电子发射时间与穿越金属厚度存在显著的非线性关系。这一发现证实了金属内部的能量色散关系强烈依赖周期性势阱的具体形式。

1 理论方法和模型

1.1 求解一维含时薛定谔方程

一维含时薛定谔方程，其解法具体如下。量子力学中描述粒子或系统随时间演化的状态都是用满足含时薛定谔方程的波函数Ψ(t)来表示的（按原子单位处理）：

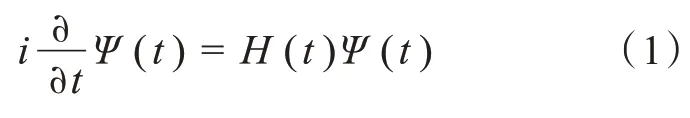
式中H表示系统的哈密顿算符，i为虚数单位。在笛卡尔坐标下系统的哈密顿量H可以表示为：

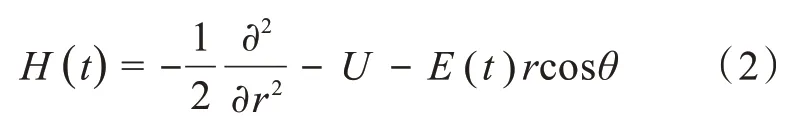
这里H(t)是指作用在约化波函数Φ(t)=rΨ(t)上的哈密顿量，E(t) =EXUV(t)+EIR(t)为线偏振入射激光场。 其中EXUV(t)为XUV 激光场强度，EIR(t)为NIR 激光场强度。

求解含时薛定谔方程的步骤一般是先给设定初始波函数Φ(t= 0)，然后将初始波函数离散化，将时间演化算符作用在初始波函数上，经过不断的迭代演化就可以获得任意时刻的末态波函数。即t时刻到t+ Δt时刻的含时演化波函数的关系表达为：

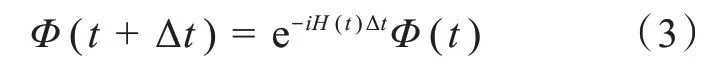
随后经过分裂算符方法，含时迭代得到末态波函数。

1.2 基于极紫外阿秒脉冲泵浦-近红外激光脉冲探测的阿秒光电子谱技术

目前在阿秒时间尺度上探测电子的超快动力学过程，主要方法有阿秒条纹相机技术和双色双光子干涉技术［5-6］。在原子的情况下，已经证明了双色双光子干涉技术和阿秒条纹相机技术都能提供相同光电子发射过程的时间信息。阿秒相机条纹技术使用的泵浦脉冲为单个阿秒脉冲，由于单个阿秒脉冲频谱分布较宽，无法区分不同光电子末态动能对应的干涉通道对光电子发射时间的影响。而双色双光子干涉技术使用XUV 阿秒脉冲链作为泵浦脉冲，阿秒脉冲链在频谱上为分立的相邻高次谐波，与观测到的阿秒光电子谱图中的一系列主峰相对应。在NIR 探测场的作用下相邻两个主峰之间形成边带峰，不同主峰和边带峰对应的干涉通道非常易于分辨。因此本文选取双色双光子干涉技术作为研究手段。

双色双光子干涉技术的具体原理是：XUV 阿秒脉冲链穿透金属表面，金属内部的束缚态电子吸收两相邻的高次谐波，逃逸金属表面时与红外激光场作用，吸收较高次（较低次）谐波的电子波包放出（吸收）一个红外光子，最终两部分波包能量一致发生干涉而记录传播相位。改变XUV 阿秒脉冲与红外脉冲之间的时间差，可以得到光电子末态动能谱与XUV 阿秒脉冲—红外脉冲时间差之间的函数关系，即所谓的双色双光子干涉谱［12-13］。

1.3 金属中的电子能量色散对光电子发射时间的影响

首先以非局域势为均匀场的单晶金属表面模型为例。利用依赖于能量的有效电子质量来表示金属中的电子色散，解析地揭示了其中的尺度规律［11］，即金属内电子输运时间与光电子发射时间之间的线性关系：

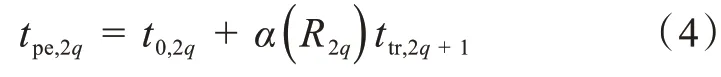
其中ttr,2q+1表示在金属内部光电子传播的时间，tpe,2q为从阿秒光电子谱图中的边带峰拟合提取的光电子发射时间，t0,2q表示与样本无关的偏移量。尺度因子α非常敏感地依赖于金属内有效电子质量的比值R2q=me,2q-1/me,2q+1。红外光子能量为ωIR，由高次谐波转换的阿秒脉冲链中的2q- 1和2q+ 1 阶谐波，对应的光子能量分别为( 2q- 1)ωIR和( 2q+ 1)ωIR，所激发电子的有效质量分别为me,2q-1和me,2q+1。除非另有说明，在本文中使用原子单位。

边带峰中心能量为kf2/2 =εi+ 2qωIR，εi记为系统的基态能量。吸收2q+ 1 阶（2q- 1 阶）谐波的电子波包放出（吸收）1 个红外光子，两部分电子波包能量一致发生干涉形成边带峰，不同干涉通道之间的总相位差为ΔΦ2q= Δξ2q(z) - Δφ2q- π -2ωIRτ。其中Δφ2q=φ2q+1-φ2q-1，π 表示红外光子的发射和吸收过程之间的相对相位。假设初始位置为z= 0，边带峰的不同干涉通道之间的空间传播相位差为：

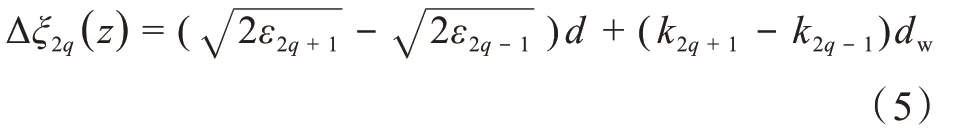
其中，d为局域电子晶格吸引势逐渐趋于零的区域，dW为金属薄片厚度。金属内部的光电子动量为，与此相对应的光电子能 量 为ε2q±1=εi+( )2q± 1ωIR，有 效 电 子 质 量me,2q±1表示色散对金属内部传播的电子波包的影响。群速度，金属内电子输运时间ttr,2q+1=dwvg,2q+1。公式（4）中与样本无关的偏移量为：

尺度因子为：

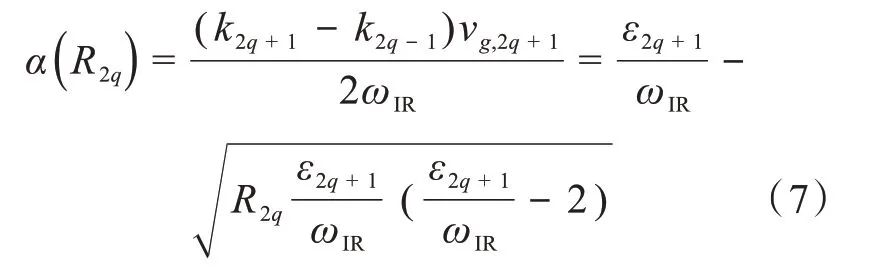
通过分离金属中电子的激发过程和传播过程，在图1 中明确地演示了金属内部的非局域电子势如何影响干涉测量的光电子发射时间。研究思路是：金属内部的束缚态电子吸收1 个XUV 光子跃迁到连续态，先穿过厚度为d的区域，势能逐渐趋于稳定；再穿过厚度为dw的金属薄片到达表面，光电子吸收或放出1 个红外光子后被探测器检测到，红外探测场被金属中的电子屏蔽在金属表面。

图1 金属模型势能图Fig.1 Potential energy diagram of metal model

2 结果与讨论

单晶金属由许多原子有序排列而成，金属内部局域的束缚态电子被激发到连续态后暴露在非局域的电子晶格弹性势中［14-15］。为了更加接近真实的金属内部势能，将金属表面模型中均匀场改为周期性势阱进行讨论。

如图1 所示，d为局域电子晶格吸引势逐渐趋于零的区域，dw为金属薄片厚度。da,dc为金属晶格参数，Zs为介于金属薄片与真空之间的表面位置。在金属薄片区域，实例A 描述金属内部光电子的自由传播，实例B 描述光电子在周期性势阱下的色散传播过程。通过调整势阱深度（势垒高度）U可改变光电子色散。 选取Yukawa potential 的原子模型吸引势作为系统的初始态，将局域电子晶格吸引势逐渐趋于零的区域设为d= 15［16］，使得势能趋于稳定后光电子进入金属内部。实例A（实例B）表示金属内部的束缚态电子吸收1 个能量为51ωIR（49ωIR）的XUV 光子跃迁到连续态，光电子到达金属表面后放出（吸收）1 个能量为ωIR的红外光子。最终两部分光电子波包获得相同的末态动能从而发生干涉形成边带峰。

红外探测场的波长设为800 nm，强度设为1 × 1011W/cm2。量子力学数值模拟中采用的空间网格步长为dx=0.1，时间步长为Δt= 0.01。计算得到的阿秒光电子谱图如图2（a）中所示，其中垂直短实线表示以延时τ= 0 为参考的光电子发射时间。拟合观测到的阿秒光电子谱图中的边带峰即可提取光电子发射时间［17］。

如图2（b）中所示，在晶格常数为da= 3,dc=2 时，由上至下3 条实线分别表示势阱深度（势垒高度）分别为U=5、0、-5 eV 的情况下光电子发射时间随穿越金属厚度的变化。垂直虚线表示当金属厚度dw= 20 时，从阿秒光电子谱图拟合提取的光电子发射时间。在本科研团队之前的研究中，模型采用了均匀场，忽略金属内部非局域的电子晶格弹性势对电子的影响，把排成晶格的正离子近似当作是均匀抹平的连续正电荷分布。而在本文中，将非局域势改为更加接近真实金属内部势能的周期性势阱。图2 中的实线说明光电子发射时间随穿越金属厚度的变化呈现显著的非线性关系（虚线为一般线性关系，与实线形成对比），这与采用了均匀场的模型所表现出的线性关系有很大不同。

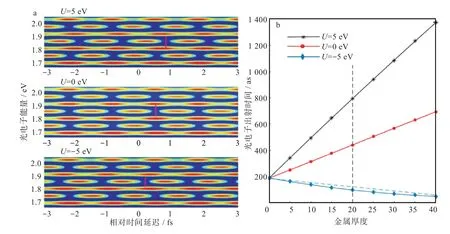
图2 （a）势能U=5 eV，势能U=0 eV 和势能U=-5 eV 时末态光电子谱图；（b）光电子发射时间随金属厚度的变化Fig.2 （a）Final state photoelectron spectrograms at potential energies of 5 eV，0 eV and-5 eV；（d）variation of photoelectron emission time with metal thickness

光电子发射时间随金属晶格常数和势阱深度的变化情况如图3 所示，图3 中虚线为各情况下一般线性关系，以作各种情况下的对比。当势阱深度为-10 eV 时，随着金属厚度的增大，光电子发射时间与穿越金属厚度的非线性变化趋于平滑。减小势阱深度直至-5 eV 时，光电子发射时间随穿越金属厚度的变化呈现显著的非线性关系，说明金属内部的色散关系强烈依赖于周期性势阱的深度。

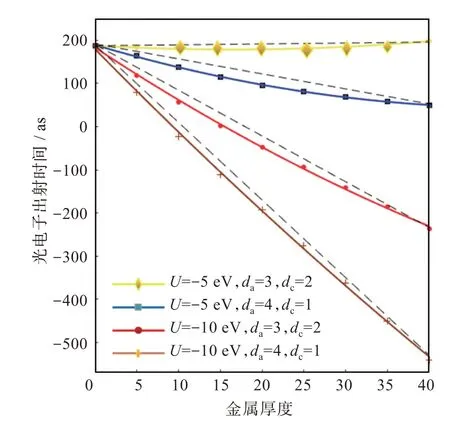
图3 光电子发射时间随金属晶格常数和势阱深度的变化Fig.3 Variation of photoelectron emission time with metal lattice constant and potential well depth

3 结 论

在本科研团队之前研究工作基础上将模型势修正为与真实固体内部相一致的周期性势能，以便更广泛地探究阿秒光电子发射时间与其能量色散之间的关系。通过数值模拟求解一维含时薛定谔方程，得到末态光电子能谱图，并对能谱图进行拟合以提取光电子发射时间。结果显示光电子发射时间强烈依赖于金属势能，尤其是与穿越金属厚度存在显著非线性关系。在以后工作中，可进一步确定周期势模型所对应的能量色散关系，从而能够更全面地分析光电子发射时间与能量色散的关系。