考虑分时电价的主动配电网经济优化调度

王国占

(珠海智和电气有限公司, 广东 珠海 519000)

0 引言

随着电网技术的发展和能源结构的改变，主动配电网(Active Distribution Network，ADN)应运而生[1]。相比传统配电网，主动配电网的结构更复杂，不仅包含各类分布式能源，还包括一些柔性负荷[2]，因此对ADN调度策略进行研究，不仅能够降低可再生能源接入对配电网的影响，还能减小配电网运行成本，提高经济性[3]。

文献[4]对主动配电网运行过程中产生的各类成本进行研究，建立了以主动配电网运行成本最小的经济优化调度模型，采用改进遗传算法对模型进行了求解，验证了模型的正确性和求解方法的优越性。文献[5]在建立ADN优化调度模型时，考虑了用户侧综合需求响应的影响，并在主动配电网中接入冷热电联供微网，以实现冷热电联供微网和ADN的最优经济调度。文献[6]为了提高主动配电网的稳定性和经济性，提出了基于改进两阶段鲁棒优化的ADN经济优化调度模型，采用实际配电网运行数据验证了模型的正确性。文献[7]以配电网电压、功率波动最小为内层目标，以环境惩罚成本和微网运行成本最小为外层目标，建立了ADN分层优化调度模型，算例分析结果表明，该调度策略提高了可再生能源的利用率和配电网系统的可靠性。主动配电网结构复杂，现有ADN优化调度模型的目标函数和约束条件有待进一步完善。

基于此，本文以ADN总运行成本最小为目标函数，考虑分时电价及配电网运行过程中的各项约束，建立包含可再生能源、储能设备和静止无功补偿装置的主动配电网经济优化调度模型，采用蚁狮优化算法对模型进行求解，以IEEE 33节点配电系统进行仿真分析，对模型的正确性及求解方法的实用性进行验证。

1 ADN经济优化调度模型

1.1 目标函数

以一天(24 h)为一个调度周期，则一个调度周期内ADN总运行成本可表示为:

minP=F1+F2+F3+F4

(1)

式中：P为FWcost为一个调度周期内ADN总运行成本，F1为配电网系统内火电机组的发电成本，F2为与上级电网的电能交换成本，F3为弃风、弃光惩罚成本，F4为储能成本。

(1)火电机组发电成本

(2)

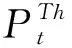
(2)电能交换成本

(3)

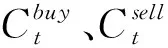
(3)弃风、弃光惩罚成本

(4)

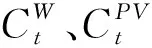
(4)储能成本

(5)

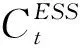
1.2 约束条件

(1)支路潮流约束

(6)

式中：pj,t、qj,t分别为注入节点j的有功功率和无功功率，rij、xij分别为支路ij的电阻和电抗，Pjk,t、Qjk,t分别为支路jk的首端的有功功率和无功功率，Pij,t、Qij,t分别为支路ij的首端的有功功率和无功功率，Iij,t为支路ij的电流，k∶j→k为以节点j为父节点的集合。

(2)风电、光伏出力约束

火电机组功率约束为:

(7)

(3)静止无功补偿装置约束

(8)

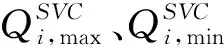
(4)节点电压约束

Umin≤Ui≤Umax

(9)

式中：Ui为节点i的电压，Umin、Umax分别为节点电压最小值和最大值。

(5)储能约束

(10)

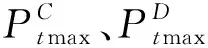
2 狼群优化算法

2013年，吴虎胜根据狼群围攻猎物的行为提出了狼群优化算法[9](Wolf Pack Algorithm，WPA)，狼群中包含头狼、探狼和猛狼，它们的职责分别是指挥、搜索和攻击。

WPA定义如下：设置狼群容量为N，空间维数为D，则狼群可表示为Xi=(xi1,xi2,…,xiD)。

(1)生成头狼，在初始解中寻找最优解Ylead，随着算法的迭代，头狼可能会被替换，如果某只狼的位置优于头狼，则将其替换，否则，头狼不变。

(2)探狼搜索，设探狼数量为M，M取决于[N/(α+1),N/α)]，其中α为探狼比例因子，探狼游走方向共有h个，游走步长为stepa，初始适应度为Yi，探狼在搜索方向p(p=1,2，…，h)上移动后的位置为:

(11)

此时计算新适应度值Yip，如果新适应度比探狼当前适应度值Yi更好，则将其替换，并更新探狼位置Xi，然后将探狼当前适应度值与头狼适应度值Ylead比较，如果探狼当前适应度值更好，则用探狼代替头狼，并召集猛狼向当前位置移动，否则继续寻优，直至最大迭代次数Tmax。

(3)猛狼移动，猛狼的数量为N-M，猛狼收到召唤信息后，会立即向头狼移动，猛狼移动步长为stepb，第k+1次迭代时猛狼的位置为:

(12)

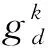
计算猛狼移动后的适应度值Yi，如果Yi比Ylead更优，则猛狼变更为头狼，并向其他猛狼发出召唤，否则猛狼继续往头狼的方向移动，直至距离头狼的位置小于dnear，则向猎物发起攻击，dnear的计算公式为:

(13)

式中：ω为距离判定因子。

(14)

攻击猎物时，如果狼群位置适应度值优于当前适应度值，则进行替换，否则不变。

步长stepa、stepb和stepc的关系为:

(15)

式中：S为步长因子。

(5)狼群更新。在狼群搜索猎物的过程中，会将适应度最差的R匹狼淘汰，并随机向狼群中补充R匹狼，R取值区间[N/(2×β),N/β]，其中β为更新比例因子。

WPA原理简单、操作方便，在寻优过程中不易陷入局部最优，具有较高的求解精度，目前得到了广泛应用。

3 WPA求解ADN经济优化调度模型

本文采用狼群优化算法对ADN经济优化调度进行求解，求解步骤如下，求解流程如图1所示。

1)设置ADN相关参数，并对WPA的相关参数进行设置，设狼数量为N，初始位置Xi，最大的游走次数Tmax和迭代次数kmax，步长因子S，距离判定因子ω，探狼比例因子α和更新比例因子β。

2)将ADN总运行成本作为适应度函数，根据式(11)对探狼游走的位置进行更新，直到探狼适应度Yi>Ylead，用该探狼替换头狼，进行下一步，否则，继续游走直到达到最大次数Tmax后进行下一步。

3)根据式(12)对猛狼奔袭的位置进行更新，直到探狼适应度Yi>Ylead，用该猛狼替换头狼，否则继续奔袭直到与头狼距离小于dnear时进行下一步。

4)根据式(14)对猎物进行围攻，并更新头狼。

5)整个狼群进行更新。

6)判断达到最大迭代次数或允许误差，若是则输出寻优结果，否则返回步骤2。

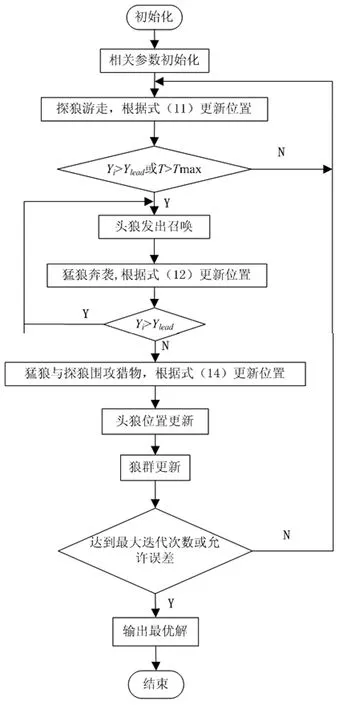
图1 改进WPA的流程图

4 算例分析

4.1 参数设置

采用IEEE 33节点系统进行仿真分析，系统参数见文献[10]。火电机组、风电机组和光伏分别接在节点4、7和13处，装机容量分别为10 MW、6 MW和3 MW，储能设备安装在16节点处，容量为3 MW，容量约束范围为20%～90%，静止无功补偿装置安装在17节点处，补偿范围为-0.02～0.02 Mvar，系统节点电压允许波动范围为0.95～1.05 p.u。ADN系统结构如图2所示。

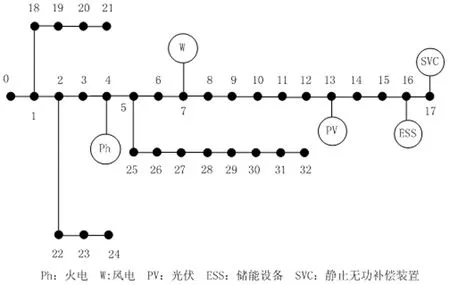
图2 ADN系统结构图

配电网与上级电网电能交换的电价从时间上进行划分[11]，具体如表1所示。

表1 峰谷电价表

调度周期为24 h，调度周期内系统负荷、风电出力和光伏出力情况如图3所示。

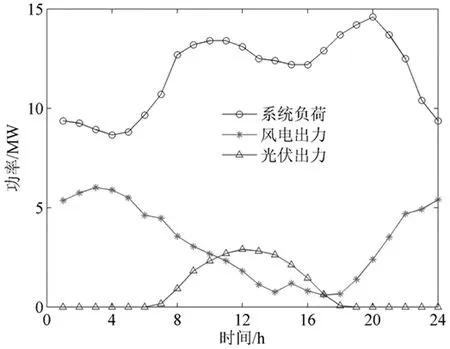
图3 系统负荷、风电光伏出力情况

狼群算法的参数设置如下[10]：N=100、kmax=200、α=4、S=800、ω=600、Tmax=20、h=4、β=5。

4.2 结果分析

采用WPA对目标函数进行求解，计算结果如图4所示。由图4可知，经过47次迭代后，WPA收敛到了最优解，此时对应的ADN总运行成本为100 197元。

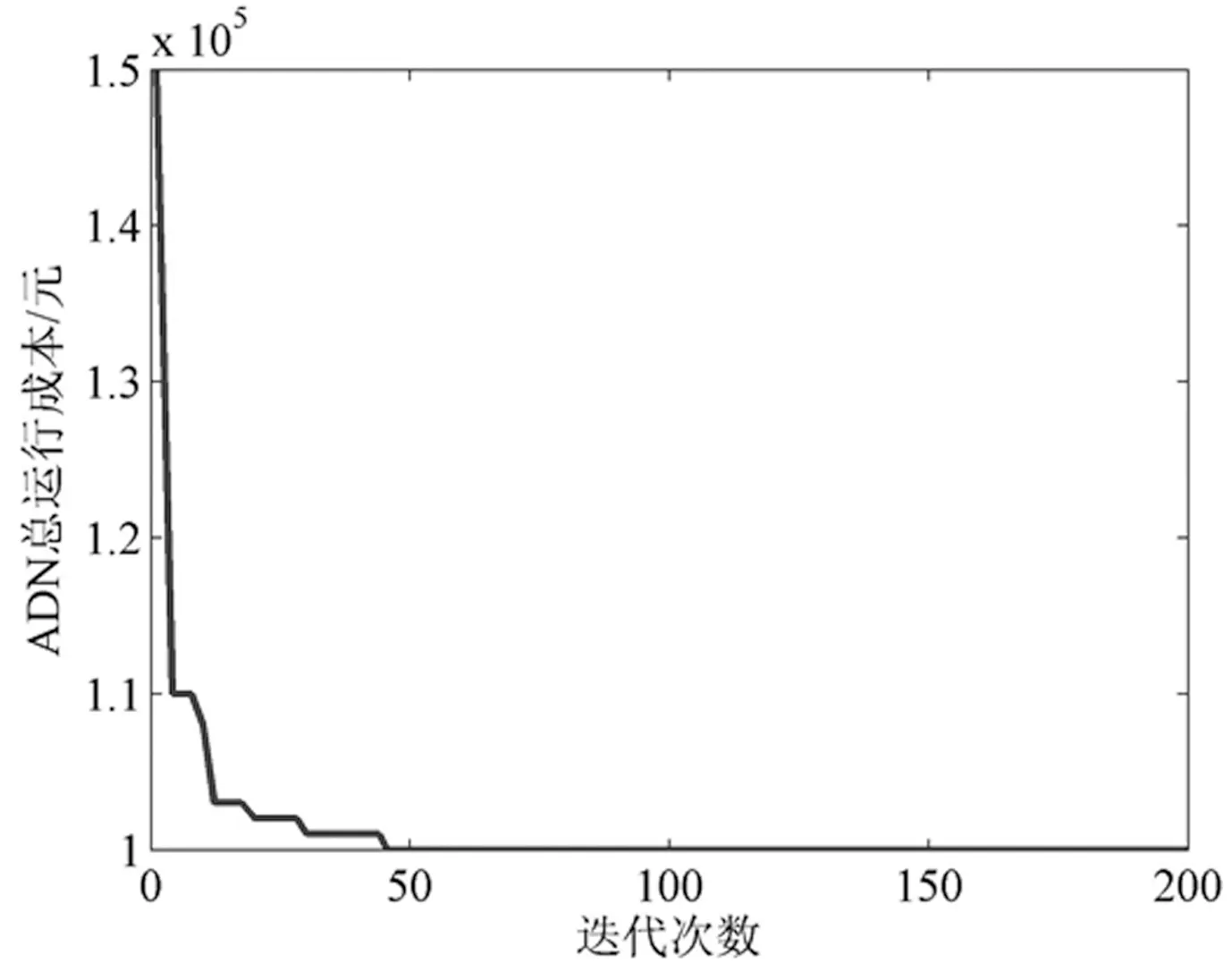
图4 WPA优化结果

表3给出了调度日当天主动配电网和传统配电网的各项成本。由表3可知，传统配电网的总运行成本主要由发电成本和电能交换成本组成，弃风、弃光惩罚成本和储能成本均为0，总运行成本为135 268元，而主动配电网的发电成本、电能交换成本、弃风、弃光惩罚成本和储能成本分别为51 094元、36 181元、10 278元和2 664元，总运行成本为100 197元，相比传统配电网，总运行成本降低25.93%，主动配电网显著提升了配电网运行的经济效益。

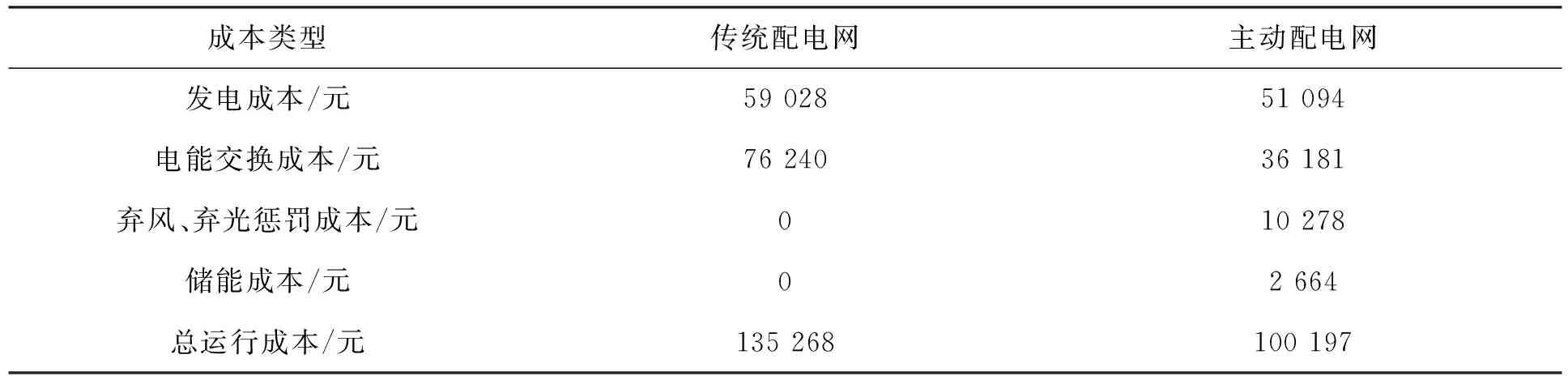
表3 主动配电网与传统配电网对比

5 结论

本文以ADN总运行成本最小为目标函数，综合考虑配电网运行过程中产生的各类成本及相应约束，并对不同时间段的购、售电单价进行划分，建立了考虑分时电价的主动配电网经济优化调度模型，采用狼群算法对ADN优化调度模型进行了求解，结果表明，ADN总运行成本为100 197元，相比传统配电网降低25.93%，验证了模型的实用性和求解方法的正确性。