DC-DC 变换器的反馈线性化反步滑模控制

张 民，韦正怡，周明珠，王凤莲，曹益畅，丁新平

（1.青岛理工大学 信息与控制工程学院，山东 青岛 266520；2.南京信息工程大学 自动化学院，江苏 南京 210044）

0 引言

电力电子变换器具有高效率、高功率密度等优点，被广泛应用于光伏发电、航天和工业制造等领域[1].作为一种典型的非线性开关切换系统，将传统的线性控制方法应用于这类变换器中往往具有一定的局限性，研究非线性控制方法在电力电子变换器中的应用是今后变换器控制技术的研究趋势[2].

基于反馈线性化的非线性控制方法得到广泛关注[3-4]，文献[5]～文献[6]将反馈线性化控制方法应用于DC-DC 开关变换器控制中，通过研究发现其具有良好的调节性能.但结合现有的研究成果可以发现，状态反馈线性化在使用过程中对被控对象的精确建模考虑了部分假设条件，并未考虑实际中存在的不确定性问题，所以其鲁棒性有一定局限性.

滑模变结构控制作为一种先进的控制方法，具有强鲁棒性[7]，在电力电子变换器控制方面也得到了大量的应用[8-9].因此，研究人员尝试将两种方法进行结合.文献[10]提出一种精确反馈线性化滑模控制方法，并以Boost 变换器为研究对象，进行仿真与实验研究，验证了精确反馈线性化滑模变结构控制具有的强鲁棒性以及抗扰动性.文献[11]提出一种基于反馈线性化的有源电力滤波器准滑模控制策略，解决了有源电力滤波器在采用滑模控制时出现的抖振现象，实验与仿真结果表明该控制方法具有较优的动态性能和稳态性能.文献[12]利用反馈线性化滑模控制技术实现了单相有源电力滤波器（APF，Active Power Fliter）补偿电流的精确控制.从对比研究结果可以发现，反馈线性化滑模控制技术具有突出的动态性能，此外，还降低了单相APF 电流总谐波失真率.

反步法采用逆序递推方法进行控制律的设计[13]，在进行每一步设计时，其将状态坐标的变化以及某些不确定参数的函数关系与设定的Lyapunov函数、虚拟控制量联系起来，并通过逐步的算法修改过程设计最终的控制律，实现系统的全局调节与控制.将反步法与滑模控制相结合，通过反步法有助于滑模面的设计，从而削弱系统的抖振现象，进一步保证系统的动态、稳态性能[14].

近年来，反馈线性化、反步法以及反步滑模控制等先进技术已经不断被应用于各种类型的电力电子变换器中，但针对反步法、反馈线性化与滑模控制技术之间的相互融合却少有研究.因此，将反馈线性化、反步法，以及滑模控制技术进行结合，并选择Boost 变换器为控制对象，探索基于反馈精确线性化的反步滑模控制技术在电力电子变换器控制中的应用，并通过仿真与实验研究分析该方法在变换器控制系统鲁棒性与抗扰动性方面的性能优势.

1 Boost 变换器数学模型

Boost 变换器随着开关管的导通和关断在不同状态之间切换见图1.图中，L1为变换器的输入电感、D1为输出二极管、C1为输出电容、S为功率开关管以及R为负载电阻，Ug与uC分别为直流输入电压及变换器输出电压，iL为变换器输入电流.开关函数定义为

式中，S为功率开关（1、0 分别表示导通与关断）；T为开关周期；D为占空比；n、n+1 分别表示第n、n+1 个开关周期.

图1 Boost 变换器原理图Fig.1 schematic of Boost converter

选取 Boost 变换器状态变量为X=[x1,x2]=[iL,uC]，输入变量为u，输出变量为h(x)=x2-uoref，根据微分几何法可以得到Boost 变换器的单输入、单输出仿射非线性系统表达式为

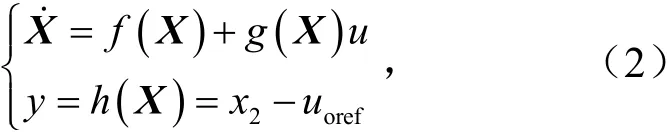
式中，X为状态变量；u为控制变量；uoref为输出电压参考值.

其中

式中，L为输入电感，μH；C为输出电容，μF；R为负载电阻，Ω.

2 Boost 变换器反馈线性化

2.1 反馈线性化条件验证

对于式（2）的仿射非线性系统，一般需要满足以下条件才可以进行反馈精确线性化[3].

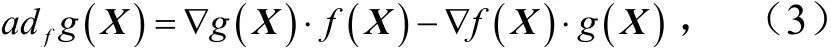
式中，

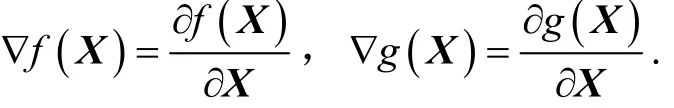
按照精确反馈线性化的条件对Boost 变换器的仿射非线性模型进行反馈线性化条件验证.

首先Boost 变换器为二维系统，因此，根据判断条件2 可知，对于向量场集合φ={g(X)}是对合的，满足状态反馈精确线性化条件（2）.此外，根据式（2）可以求得Boost 变换器向量场f(X)对g(X)的李括号为

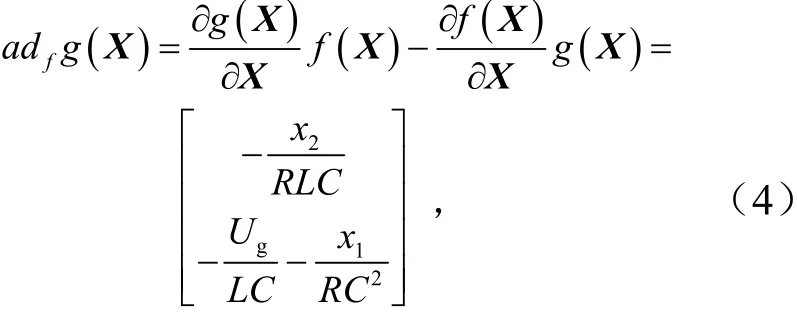
所以，可得到状态反馈精确线性化验证条件矩阵为

根据式（5）可知，[g(X)adfg(X)]的秩为2，等于系统的维数.因此，满足状态反馈精确线性化验证条件（1）.综上所述，满足状态反馈精确线性化条件，所以Boost 变换器系统可以进行状态反馈精确线性化，从而实现状态反馈精确线性化控制.

2.2 坐标变换及布鲁诺夫斯基标准型

依据状态反馈精确线性化判定条件及式（2）定义的输出函数，可计算系统的关系度为

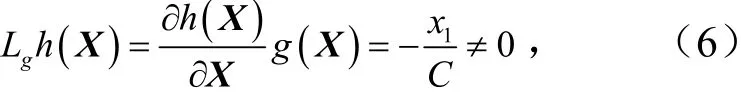
式中，Lgh(X)为输出函数h(X)对向量场g(X)的李导数.

由式（6）可知，在X≠0 处系统的关系度r=1≠n.因此，根据状态反馈精确线性化坐标变换要求，式（2）所定义的输出函数h(X)无法通过坐标变换进行状态反馈精确线性化.所以，必须重新构造一个新的输出函数ω(X)，从而满足系统关系度r等于系统维数n的坐标变换要求.此外，新构造的输出函数ω(X)必须满足

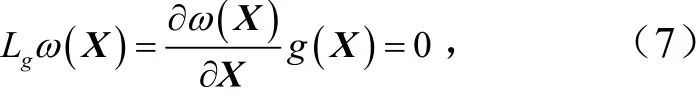
将式（2）代入式（7），可得

求解式（8）可以得到1 个满足要求的解为

由计算出的ω(X)可得到向量场对应李导数为

由式（10）可知，在X≠0 时，所求的新输出函数ω(X)使得系统的关系度r=2=n，满足系统关系度等于系统维数的要求.因此，可以利用输出函数ω(X)进行状态反馈精确线性化坐标变换.

定义坐标变换为

经坐标变换后，取其布鲁诺夫斯基标准型为

式中，z1，z2为经坐标变换后系统新的状态变量；v为系统新的控制量.按照反馈精确线性化理论可得原系统控制量u与新的控制量v的关系为

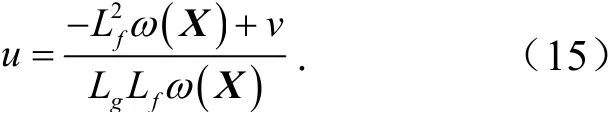
3 反步滑模控制器设计

经过上述精确反馈线性化后，原非线性系统被转换为能控型线性系统.为了实现输出电压uo跟踪参考电压uoref，在Boost 变换器达到稳态时，可以得到电感电流参考值为

在进行反步滑模控制器设计时，需要定义新的跟踪误差为

反步法将1 个严格满足反馈要求的非线性系统划分为n维子系统，采用逆推的方法为每一个子系统设计1 个李雅普诺夫函数，并通过设置虚拟控制量，逐步修改函数算法，调整控制量，最终实现整个系统的全局稳定[14]，从而保证系统稳、动态性能.

下面采用反步法设计Boost 变换器系统的滑模控制器.由于Boost 变换器是1 个二维系统，所以需要采用两次反步法.

（1）定义Lyapunov 函数为

对式（18）求导，并结合式（17）可以得到

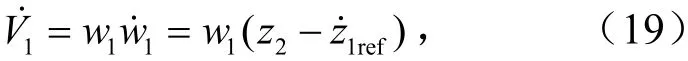
设置x1子系统的虚拟控制量为

式中，c1控制常数，c1＞0.

从而可以得到

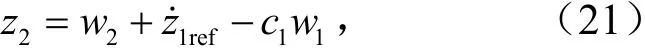
由式（19）、式（21）可得

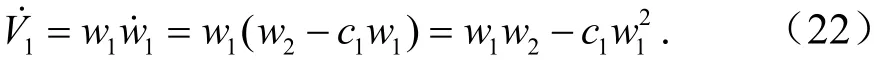
（2）定义Lyapunov 函数为

对式（23）求导，可得

对式（20）求导，并利用式（14）、式（15）可得

将式（25）代入式（24）可得

根据滑模控制理论与反步法，设计反步滑模控制器[14]，根据式（20）可知，x1子系统的虚拟控制量w2受输出跟踪误差信号w1与参考信号x1ref的影响.所以，根据控制要求，选取滑模面为

选取滑模趋近律为

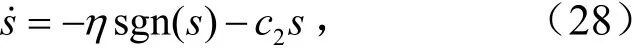
式中，η、c2为可调整的控制系数，且η＞0；c2＞0.

结合式（26）、式（27）与式（28）可以得到Boost 变换器基于状态反馈线性化的反步滑模控制律为

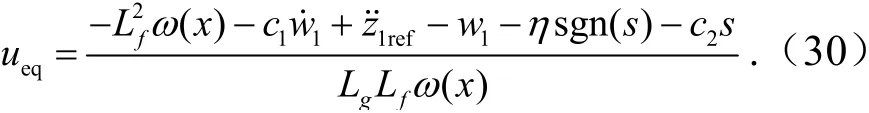
根据李雅普诺夫稳定性定理[3]，分析Boost 变换器反步滑模控制系统的渐近稳定性.

将式（30）代入式（26）可得

根据李雅普诺夫第二法稳定性判据可知[3]：若为负定或者半负定时，对于任意初始状态x(t0) ≠ 0而言，除去x= 0外，对x≠ 0，不恒等于0.则可以称原点平衡状态是渐近稳定的.如果进一步，当则该系统是大范围渐近稳定的.

由式（31）可知，V˙(w)是负定的，且在(w1,w2)≠(0,0)处，V˙(w)不恒等于0.所以，Boost 变换器反步滑模控制系统是渐近稳定的，即由式（14）、式（17）、式（20）与式（30）构成的控制系统也是渐近稳定的.因此，Boost 变换器的控制系统可以实现对参考目标信号进行有效的跟踪控制.

至此，Boost 变换器的反馈精确线性化反步滑模控制系统设计完成.系统的控制原理示意见图2.

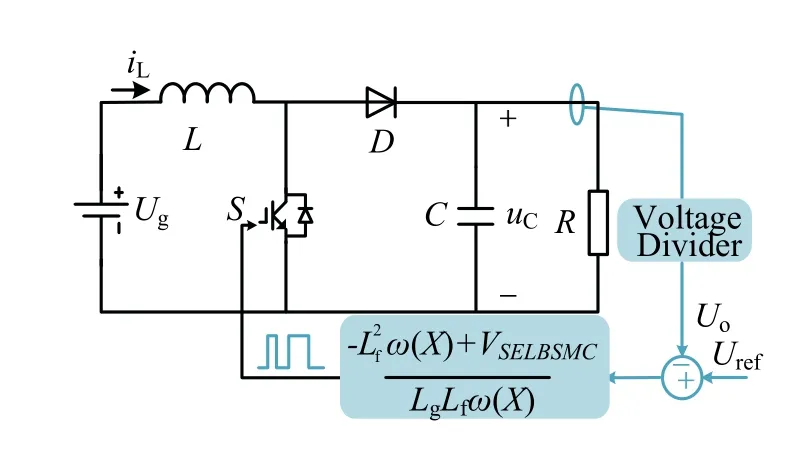
图2 Boost 变换器控制系统控制原理Fig.2 control principle of Boost converter control system

4 仿真与实验验证

4.1 仿真实验

为验证反馈线性化反步滑模控制方法的正确性与有效性，利用Simulink 搭建Boost 变换器反馈线性化反步滑模控制系统进行仿真，并与PID 控制方法进行对比，系统仿真参数见表1.表1 中，Uref为参考电压值，fs为开关频率.

表1 系统仿真参数Tab.1 system simulation parameters

根据表1，设计反馈线性化反步滑模控制参数c1=2 000，c2=15 000，η=20 000.在设计Boost 变换器的PID 控制器参数时，采用小信号建模方法，并利用Bode 图补偿进行PID 参数的校正[15]，并借助Matlab 中sisotool 工具箱得到PID 控制器参数为

系统仿真分别在起动响应、输入电压切换、输出负载切换、参考电压切换、输入电感切换几种情况下进行.

（1）系统起动响应

Boost 变换器的反馈控制起动响应对比见图3.

从图3 分析可知，在确保控制系统无超调、无振荡的条件下，在本文所提出的反馈线性变化反步滑模控制办法（SFLBSMC，Feedback Linearization Backstepping Slidding Mode Control）控制下的Boost变换器的起动响应效果要优于PID 控制，起动过程速度快，调节时间为5 ms 左右，而PID 控制方法则需要64 ms 左右起动.SFLBSMC 控制下的Boost变换器过程无明显的超调，而PID 控制下有明显的超调.同样在SFLBSMC 控制下，电感电流也很快到达新的稳态值，动态效果明显优于PID 控制.验证了SFLBSMC 的鲁棒性以及超调小的优势.

图3 2 种控制方式起动响应对比Fig.3 two control methods start response comparison

（2）输入电压切换响应

系统仿真时，在0.5 s 时突加5 V 的电压扰动，并在0.35 s 时去掉该扰动.图4 为SFLBSMC 和PID控制下Boost 变换器输出电压和电感电流波形.

图4 2 种控制方法输入扰动下的动态响应对比Fig.4 comparison of dynamic response of two control methods under input disturbance

图4（a）、图4（b）对比可知，输入电压扰动存在时，在反馈线性化反步滑模控制下，Boost 变换器输出电压大约经过5 ms 就达到了设定的稳态值.而在PID 控制方式下，Boost 变换器经过大约70 ms 才达到设定的稳态值，而且超调量也较大.

与此同时，电感电流在SFLBSMC 控制下的响应速度明显优于PID 控制.这也进一步验证了反馈线性化反步滑模控制的优势.

（3）参考电压切换响应

通过系统仿真验证参考电压突变下的动态响应，扰动量为5 V.仿真结果见图5.

图5 2 种控制方式参考电压扰动下的动态响应对比波形Fig.5 comparison of dynamic response of two control methods under reference voltage disturbance

从图5（a）可知，参考电压发生变化后，SFLBSMC 控制下，输出电压经过大约6.5 ms 达到新的稳态状态，PID 控制需要大约75 ms，控制效果明显劣于SFLBSMC 控制.

从图5（b）也可以分析出，SFLBSMC 控制下，电感电流的调节时间明显优于PID 控制.

（4）负载切换响应

为模拟负载扰动，将2 个不同阻值的电阻并联，并利用一个理想开关进行切换控制.仿真时分别在0.15 s、0.3 s 将负载在50 Ω 和40 Ω 间各切换一次.系统的仿真结果见图6.

由图6（a）可以看出，在SFLBSMC 控制下，Boost 变换器的输出电压经过大约7 ms 就达到了稳态值，调节时间短、超调小.而PID 控制则需要经过大约70 ms 的时间才达到稳态值.SFLBSMC 的调节效果明显优于PID 控制.同理，对于电感电流，由图6（b）分析可知，SFLBSMC 的控制效果要明显优于PID 控制.

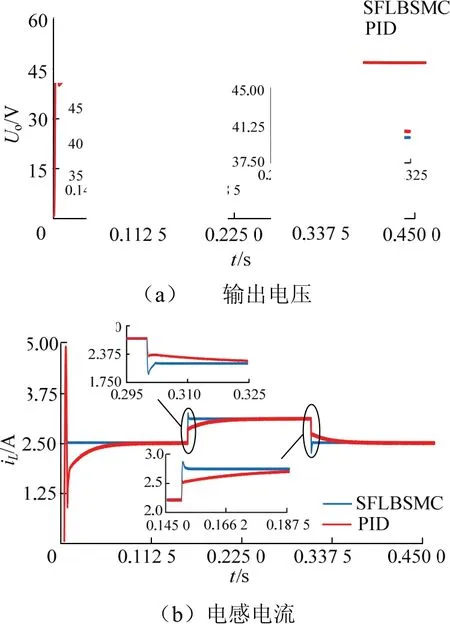
图6 2 种控制方式负载扰动下的动态响应对比Fig.6 comparison of dynamic response of two control methods under load disturbance

将4 种不同仿真方式下的2 种控制方式到达稳态定值的调节时间列于表2，其中仿真1、仿真2、仿真3、仿真4 分别代表起动响应仿真、输入电压切换仿真、参考电压切换仿真，以及负载切换仿真.从表2 的数据中也可以看出，所设计的SFLBSMC控制方法调节时间短，具有较强的鲁棒性.

表2 仿真调节时间对比Tab.2 comparison of simulation adjustment time

（5）输入电感变化下的鲁棒性

为了验证SFLBSMC 的鲁棒性，在电感值逐渐变大的情况下，保持两种控制方式的控制参数不变，分析2 种控制方法下Boost 变换器的起动响应过程.

图7为电感L取1 mH、5 mH、10 mH 时， Boost变换器起动时输出电压波形.由图 7 可知，在SFLBSMC 控制下，随着输入电感值的增大，系统响应速度变慢，调节时间变长，并有一定的超调，但是系统均能达到稳态值.此外，响应速度、调节时间指标均优于PID 控制.

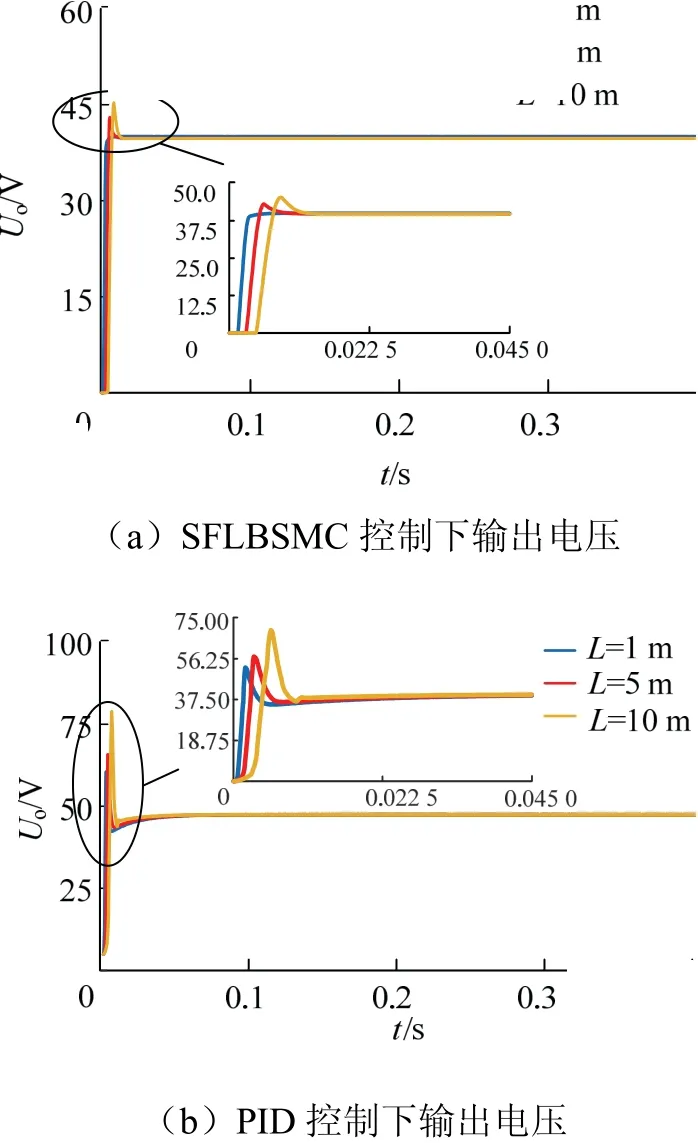
图7 不同电感值下2 种控制方法起动响应对比Fig.7 comparison of start-up response of two control methods under different inductance values

通过以上对比分析可以得出，SFLBSMC 控制的鲁棒性要明显优于PID 控制.

4.2 实验验证

为验证实际工作中控制系统的有效性与可行性及前文理论分析的正确性，采用TMS320F28335作为主控芯片搭建实验平台，见图8，控制参数与仿真一致，样机实验参数与仿真参数一致，见表1.实验分别验证SFLBSMC 与PID 控制下Boost 变换器的稳态特性以及输入电压切换控制效果.

图8 样机实验平台Fig.8 prototype experiment platform

（1）稳态特性

图9为稳态时输入电压与输出电压波形，可以看出，SFLBSMC 控制下电压输出纹波较小，没有出现较严重的毛刺现象.

图9 2 种控制方式下的稳态响应波形Fig.9 steady-state response waveform under two control modes

（2）输入电压切换特性

图10（a）、图10（b）为在输入电压切换下，2种控制方式的实验对比波形，电压幅值变化量为5 V.

从图10 可以看出，当输入电压由20 V 切换至25 V 时， PID 控制下，Boost 变换器输出电压到达稳态值所需时间约为40 ms，而在SFLBSMC 控制下，输出到达稳态值只需大约10 ms，调节时间远短于PID 控制，且调节过程较为平缓，没有出现较大的振荡.从图10（c）、图10（d）可以发现，当输入电压由25 V 切换至20 V 时，PID 控制调节时间大约为25 ms，而SFLBSMC 控制大约为6 ms，调节过程快速、平缓.

图10 2 种控制方式下输入电压切换响应波形Fig.10 input voltage switching response waveform under two control modes

通过试验对比分析，SFLBSMC 控制的鲁棒性优于PID 控制，同时也验证了前文理论分析的正确性.

表3为2 种输入电压切换实验条件下，2 种控制方法到达稳态值的调节时间.由表 3 可知，SFLBSMC 控制调节时间明显短于PID 控制.

表3 试验调节时间对比Tab.3 comparison of test adjustment time

5 结论

将反馈线性化、反步法以及滑模控制技术进行结合，设计了一种反馈线性化反步滑模控制方法，并以Boost 变换器为控制对象，分析系统稳定性.通过仿真与实验验证所提出的控制方法具有以下特点.

（1）反馈线性化反步滑模控制方法由于结合了多种方法的优点，具有较强的鲁棒性，面对扰动能够快速到达设定的稳态值，调节时间短.

（2）所设计的方法较为简单，便于实现.