基于CFD 流线型桥梁断面二维涡激振动分析
宋红红,杨 刚,姜亚丽
(大连海事大学 交通运输工程学院,辽宁 大连 116026)
0 引言
涡激振动是由风荷载作用在桥梁断面气流分离出旋涡及脱落产生,当旋涡脱落频率与桥梁自振频率相等时易产生涡激共振现象.流线型箱梁具有较好的抗颤抖振功能,但是大跨度的流线型箱梁在较低风速下易产生涡激共振现象[1].涡激共振现象虽然不会像颤振和驰振那样对桥梁产生动力失稳破坏,但是由于涡激振动发生的风速低,频率高,长时间的涡激共振现象会造成桥梁构件疲劳损坏,影响行车舒适性和行车安全[2].近几年国内外桥梁涡激振动现象并不少见.如英国Kessock 大桥因涡激振动引起110 mm 的竖向位移;2012 年,江西九江长江公铁两用钢拱桥发生吊杆涡激共振现象;2013年,上海杨浦大桥发生拉索共振、风雨振现象[3];2020 年,武汉鹦鹉洲大桥、广州虎门大桥都因涡激振动作用产生较大起伏,严重影响行车安全.
桥梁涡激振动的研究方法主要有风洞实验、数值模拟、现场实测、理论分析.通过这几种方法对涡激振动的产生机理、涡激振动的影响因素、涡激振动的计算方法、涡振控制进行研究[4].基于CFD(Computational Fluid Dynamics)建立桥梁数值风洞技术已经逐步成熟[5-10].文献[1]中采用数值风洞的方式,避免了实际风洞尺寸的限制,研究了涡激振动阻塞比效应.文献[11]中发现了高宽比较大的流线型箱梁断面涡振的发生机制.文献[12]中将高宽比为4 的矩形断面涡激振动响应结果与风洞试验比较,结果吻合较好,证明采用CFD 技术进行涡激振动研究的可行性.还有学者将CFD 与风洞试验相结合提出一种新的研究方法[13-14],通过这种方法对半开口分离双箱梁的涡激性能及气动措施进行了探讨[2].尽管桥梁涡激振动方面的研究已经取得一些重要成果,但是由于不同桥梁产生涡激振动的机理不同,影响涡激振动的因素繁多,因此,对于受风环境影响严重的桥梁有必要分析其涡激振动的机制,找到高效模拟风环境和进行涡激振动模拟的求解方法,为预防桥梁涡激共振和涡激振动应急处理打下基础.
大连长山大桥为大跨度预应力混凝土矮塔斜拉桥,主梁采用流线型扁平箱梁,主桥长度1.79 km,主跨长540 m,横跨长山海峡,由于其跨径大和近海的地理位置使其受风荷载的影响非常明显.此外,在大桥的设计过程和现有的研究中并没有考虑涡激振动的影响.因此,对大连长山大桥进行涡激振动分析非常有必要.采用CFD 技术对长山大桥主梁截面进行二维涡激振动研究,探究其脱涡过程及涡激共振的可能性,为评价本桥的抗风性能提供一定的参考依据.
1 数值方法与计算模型
1.1 涡激振动计算方法
将桥梁截面涡激振动模型简化为竖向单自由度弹簧-质量-阻尼系统,见图1.
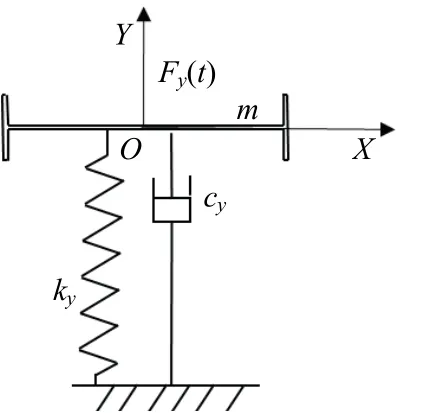
图1 单自由度弹性支承柱体结构涡激振动模型Fig.1 viv model of a two-degree-of-freedom elastic supported column structure
单自由度弹性支撑体结构涡激振动控制微分方程为
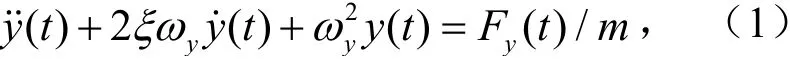
式中,y(t)为t时刻的振动位移,m;y˙(t) 为t时刻的振动速度,m/s;˙y˙(t) 为t时刻的振动加速度,m/s²;m为单位长度柱体的质量为弹性支承柱体的振动系统的阻尼,N/(m·s-1);ξ为弹性支撑体系阻尼比;为弹性支承柱体的振动系统的刚度,N/m;ωy为弹性支承柱体的振动系统的振动圆频,Hz;Fy(t)为t时刻单位长度柱体所受到的竖向力.
粘性不可压缩流体的控制方程有质量守恒方程(连续性方程)、动量守恒方程(N-S 方程)和能量守恒方程.在进行涡激共振响应计算时不考虑能量方程,在直角坐标系下,基于雷诺平均连续性方程和N-S 方程分别为
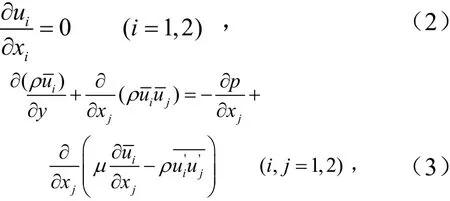
式中,ρ为空气密度,取1.225 kg/m3;μ为动力粘性系数,取1.789 4×10-5kg/m·s;u、p分别为流场速度和压力的时间平均值,为雷诺应力.
1.2 计算模型
(1)二维流场及网格划分
以长山大桥典型主梁截面为研究对象,流场计算域布置及桥梁截面分别见图2、图3.计算域采用圆形流场,可避免漩涡打到边界上再折射回来,并保证流体在流场内充分绕流.计算域边界距离截面形心一般为20 倍的特征长度,因此设置圆形流场外缘距截面形心为20 倍的截面宽度;入口的边界条件设置为速度入口(Velocity inlet),通过给定初始速度来模拟来流风速,出口边界设置为压力出口(Pressure outlet),将其与大气压的压差设置为0 来模拟出口边界与外界相通.
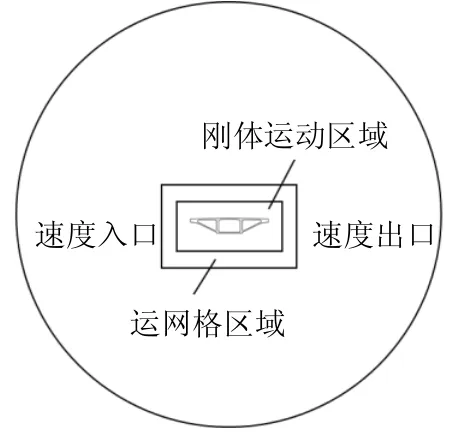
图2 计算域及边界条件布置Fig. 2 clculation field and boundary condition layout
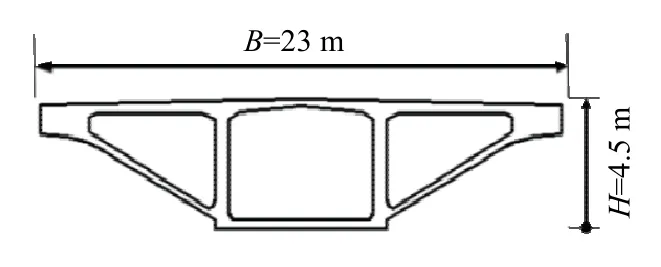
图3 主梁截面Fig. 3 schematic of main beam section
由于桥梁截面形状相对复杂,该模型采用三角形非结构化网格,见图4、图5.网格划分采用嵌套网格方式,将桥梁截面视为刚体,截面外围分别为刚体运动区域、动网格区域、静网格区域.在靠近截面的地方网格密度较大,最小网格面积约为0.052 m2,流域外围网格密度较小,最大网格面积约为2.03 m2,这样既能保证计算精度,又能通过减少网格数量来提高计算效率.

图4 整体网格示意Fig. 4 overall grid diagram

图5 局部网格示意Fig.5 ocal grid diagram
(2)求解设置及计算流程
结构涡激振动求解过程采用Fluent 里的SST k-ω湍流模型进行模拟.具体求解设置为:采用SIMPLEC(Semi Implicit Method for Pressure Linked Equation Consistent)算法求解动量方程中速度分量和压力耦合问题;采用PRESTO(Pressure Staggering Option)求解速度分量;对流项采用QUICK(Quadratic Upwind Interpolation For Convection Kinetics)求解.单自由度弹性支撑结构涡激共振计算流程见图6.
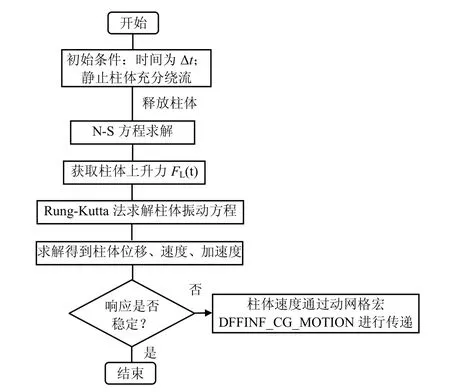
图6 涡激振动计算流程Fig. 6 viv calculation flow chart
进行结构涡激共振计算时,首先对结构进行静态绕流计算,然后释放截面某方向的自由度,进行瞬态动力分析,得到每个时间步内结构上的升力、升力矩、压力分布等,并将该升力代入式(1),采用Runge-kutta 法求解柱体振动响应,再将结构动力响应赋给结构周围的流体,然后通过Fluent 中动网格宏DEFFINE_CG_ MOYION 进行传递,使结构周围的动网格获得速度,从而更新网格位置.待网格迭代收敛后,整个流场更新完成,然后进行下一个时间步的计算,直到计算结束.
(3)动力求解方法
通过UDF 将迭代求解方法嵌入到Fluent 中求解式(1),采用Runge-kutta 迭代求解方法,其表达式为
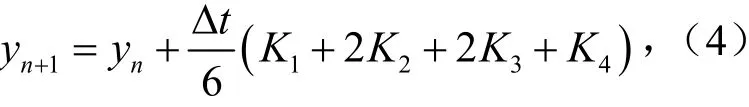
式中,
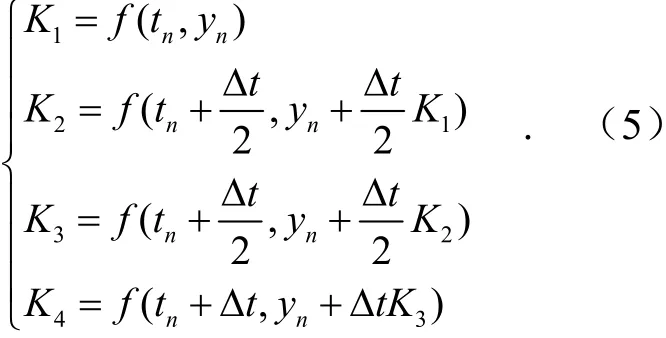
采用四阶Runge-kutta 对二阶结构振动微分方程进行求解,首先要把二阶微分方程进行降阶处理,因此可设为

将式(6)代入式(1)得
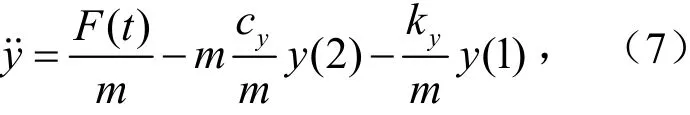
即
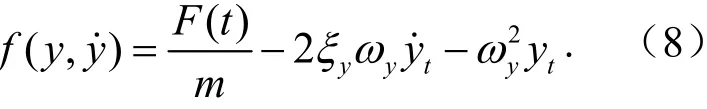
经计算,可得结构在下一时间步的位移为
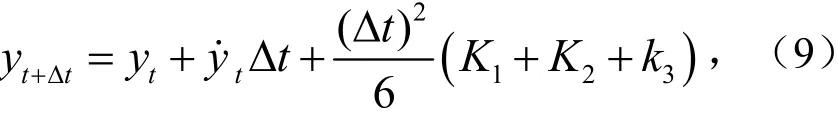
速度为
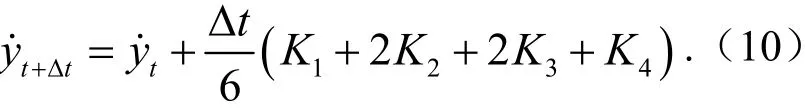
式(9)~式(10)中,
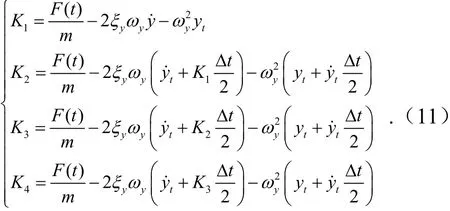
2 长山大桥主梁截面涡激振动分析
2.1 静态绕流分析
在静态绕流过程中,流场入口采用速度入口的边界条件:设置湍流强度为0.5%,湍流粘性比为10%,风速为10 m/s,即折算风速为
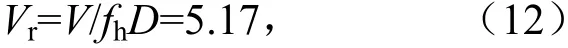
式中,V为来流风速,m/s;fh为结构自振频率,Hz;D为截面高度,m;流场出口采用压力出口的边界条件.设计算残差为5×10-4,步数为5 000,得到静态绕流三分力时程,见图7.从图7 中可以看出,在计算2 500 步后三分力系数呈周期性变化,表征流场达到稳定状态.
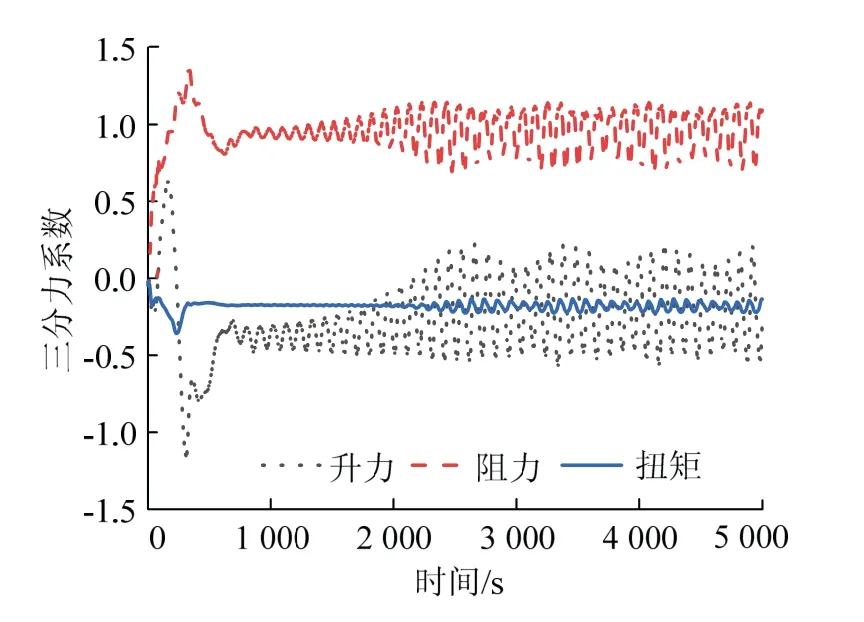
图7 三分力系数时程Fig.7 time history of three component force coefficient
2.2 涡激振动分析
涡激振动分析采用1.2 节中的求解设置,选择与静态绕流相同边界条件,关闭静态分析,开启瞬态分析进行求解,导入UDF 程序完成控制方程求解及网格更新.长山大桥模型一阶竖弯频率为0.43Hz,风攻角为0°,主梁断面质量为57 980 kg/m,设置时间步长为0.01.
通过Fluent 动态捕捉,得到一个周期内的脱涡过程,见图8.
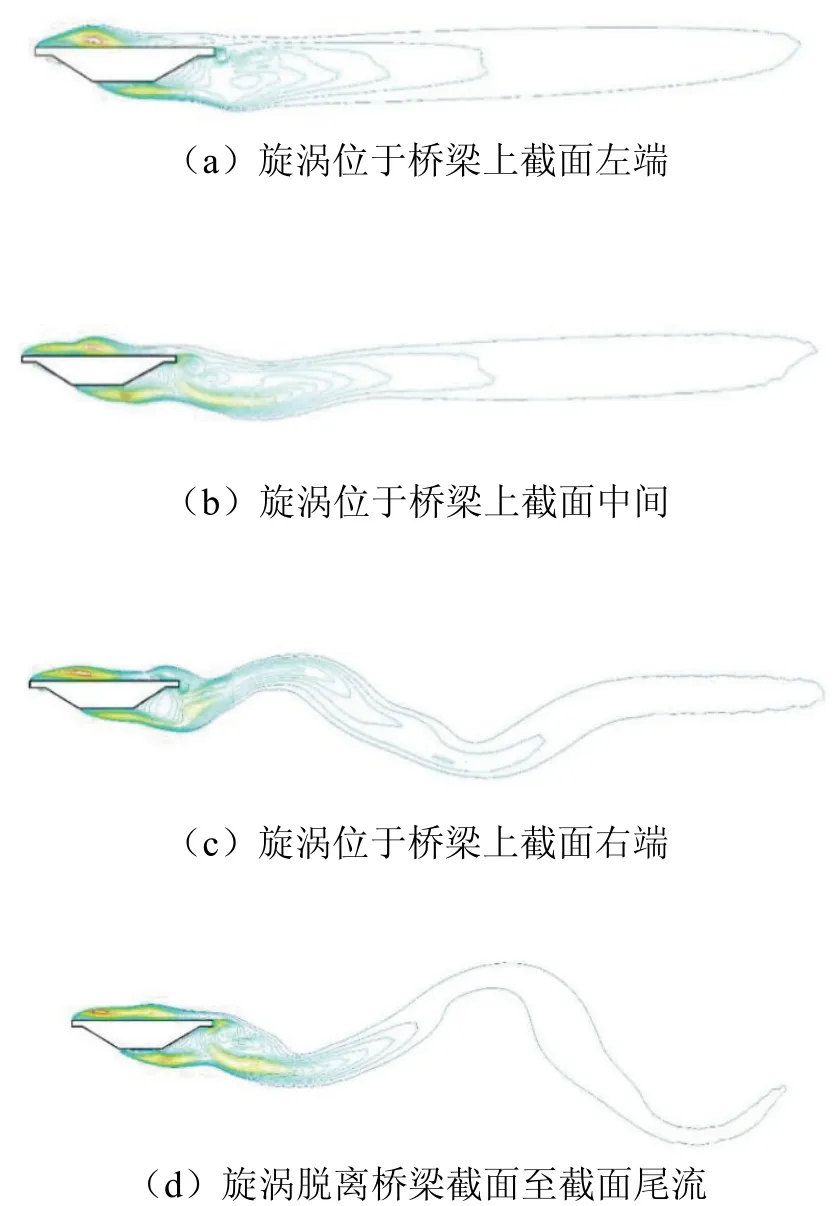

图8 脱涡过程Fig. 8 vortex shedding process
由图8 中可见,旋涡首先产生在桥梁上截面风速入口处,然后顺着风速风向慢慢向右推移至桥梁上截面中间位置,随后转移到桥梁截面尾部,最后旋涡脱落在桥梁截面尾部流场中.从旋涡脱落的整个过程中可以发现,在桥梁上截面和下截面及截面尾部涡量较大.图9 为折算风速为12 的涡量图,对比发现不同的风速下产生的涡量和脱涡频率不同,风速为12 时桥梁截面尾部流场产生的旋涡较多.

图9 折算风速12 涡量Fig. 9 translate wind speed 12 vorticity
Strouhal 通过实验发现当流体流过圆柱后,在尾流中将出现交替脱落的旋涡,并且旋涡脱落的频率、风速及圆柱体直径之间存在以下关系

式中,fs为旋涡脱落频率,Hz;D为圆柱体直径,mm;U为来流速度,m/s2;St为Strouhal 数.后经学者研究发现,式(13)也可用于桥梁,其中D为桥梁迎风面主梁高度.
按照以上方法,分别对折算风速4、6、8、10、12、14、16、18、20、22 这10 种风速下进行涡激振动计算.限于篇幅,仅给出8、10、12 风速下升力时程和升力频谱分析结果,见图10~图12.从图10~图12 可以看出,随着风速的增大脱涡频率逐渐增大,符合式(13)中风速与脱涡频率呈线性增加的关系.
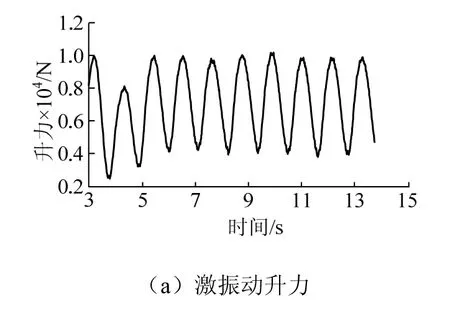
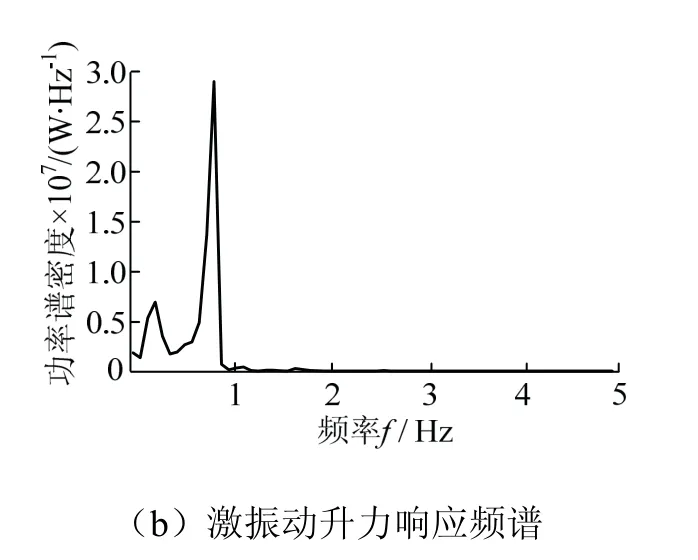
图10 折算风速8 涡激振动响应Fig. 10 translate wind speed 8 viv response
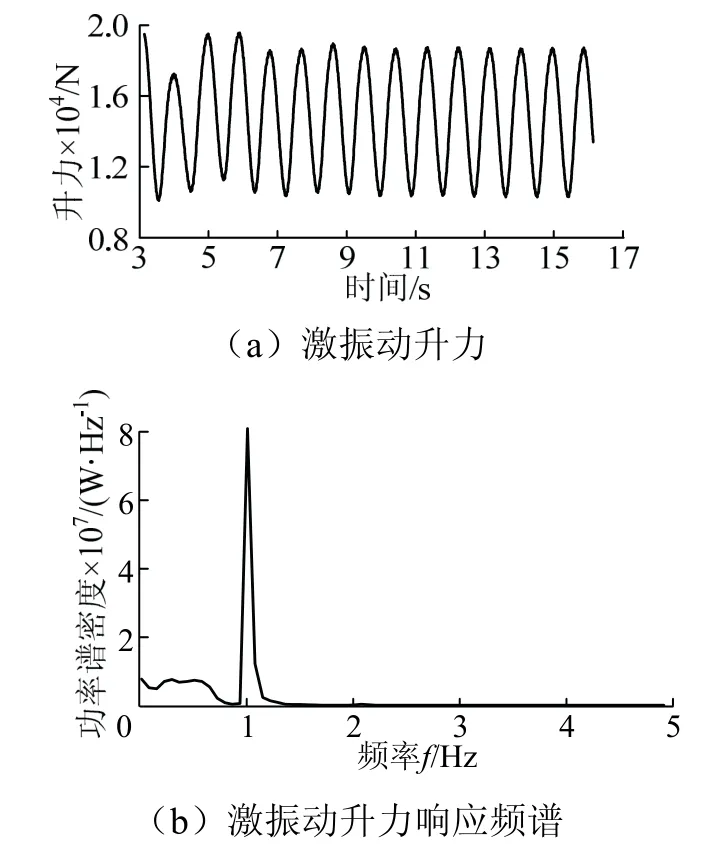
图11 折算风速10 涡激振动响应Fig. 11 Translate wind speed 10 viv response
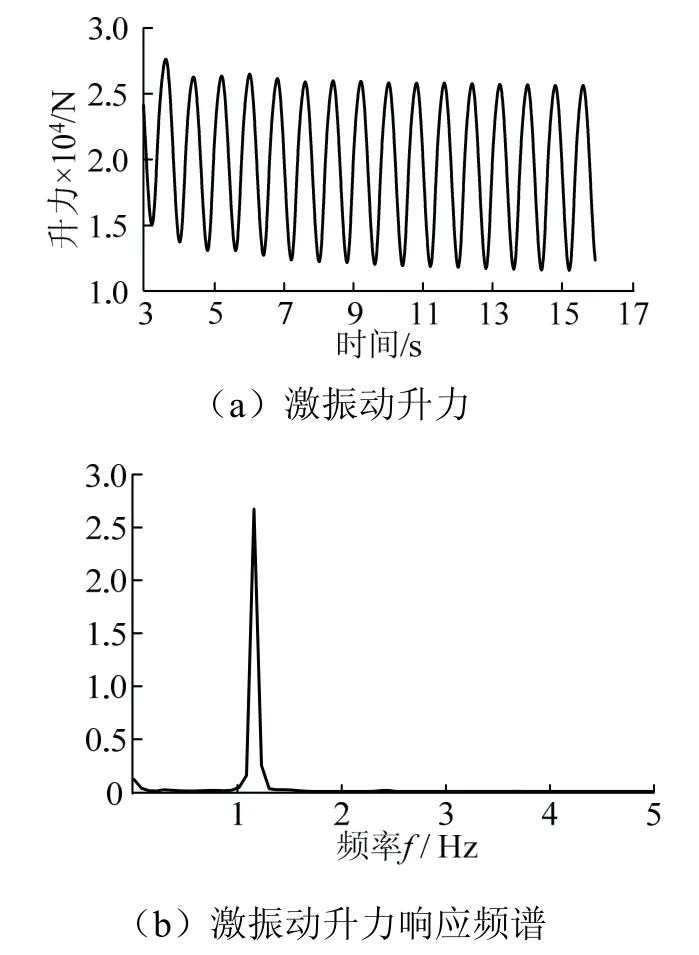
图12 折算风速12 涡激振动Fig. 12 translate wind speed 12 viv response
图13为竖向位移与折算风速关系,从图中可以看出,涡振锁定折算风速区间为8~20,引起的竖向无量纲位移为0.023,此时脱涡频率为1.43 Hz,与本桥竖向自振频率0.43 Hz 相差较大,不易出现涡激共振现象.
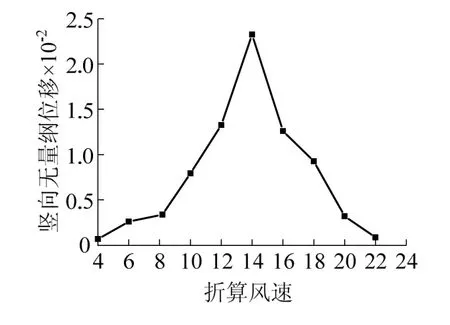
图13 位移随风速的变化Fig.13 displacement changes with wind speed
3 结论
基于Fluent 动网格技术对长山大桥典型主梁截面进行二维流场涡激振动模拟,得到以下结论.
(1)采用“桥梁截面+运动区域+动网格区域+静止网格区域+流场边界”的二维流场建模方式能够有效防止负网格的产生,并且能够减少网格数量,提高计算效率.
(2)对桥梁截面进行了折算风速为4、6、8、10、12、14、16、18、20、22 这10 种风速下单自由度涡激振动模拟,分析得到易引起涡激振动的折算风速为8~20 之间,竖向无量纲振幅最大为0.023,此时的脱涡频率为1.43 Hz,与本桥竖向自振频率相差较大,不易出现涡激共振现象.
(3)流线型箱梁的漩涡产生脱落过程为:产生于桥梁截面入风端,经桥梁上截面,移至截面尾部,最后脱落在截面尾部尾流中.因此,今后在改变流线型箱梁前端的截面形状时,如大型风屏障或者大型货车停靠时,应注意桥梁的涡激振动情况,避免发生共振.

