基于生成对抗网络的交通流参数实时估计模型

姚荣涵，王荣贇，张文松，叶劲松，孙锋

(1.大连理工大学，交通运输学院，辽宁大连 116024；2.交通运输部科学研究院，综合交通运输大数据应用技术交通运输行业重点实验室，北京 100029；3.山东理工大学，交通与车辆工程学院，山东淄博 255049)

0 引言

随着城市化与机动化进程加快，城市交通需求与供给矛盾日益加剧，伴随而来的交通拥堵和环境污染等问题严重影响城市可持续发展。智能交通系统借助海量出行数据及先进信息技术，将交通运行状态实时分享给道路使用者，从而提高道路时空资源利用率。交通运行状态依赖于交通流参数，其精准估计有利于交通管控策略的制定，帮助道路使用者提前规划出行路线，还能为高需求区域调配更多公共资源。

众所周知，交通流数据具有明显的时空相关性[1]。经典的历史平均模型和长短期记忆(Long Short-Term Memory,LSTM)神经网络等只能考虑交通流的时间相关性，无法考虑交通流的空间相关性，以致忽略了上下游交通运行状态之间的关联。因此，需进一步提高交通流参数估计的精度。

道路网中各路段相互连接，目标断面交通流主要受其上下游交通流影响。因此，越来越多的研究者开始考虑道路网空间相关性对交通流及其参数估计的影响。CNN模型有局部连接和权值共享的特点，ZHANG 等[2]和YAO 等[3]基于此特点利用CNN模型提取网格化道路网的交通流参数的空间特征。

道路网空间不同于一般的欧式空间，车辆移动必须途径道路，因此，道路网空间更适合表达为图结构。YU等[4]、LIAO等[5]及陈喜群等[6]将道路网描述为基于距离的无向图结构，利用图卷积神经网络通过考虑道路之间的连接关系估计交通流参数，往往比卷积神经网络拥有更好的性能表现。

GOODFELLOW 等[7]提到的生成对抗网络(Generative Adversarial Network,GAN)自2014年提出后成为新的研究热点，通过生成器与判别器之间的博弈，使得生成器能够生成真实数据。GAN 模型最初被应用于图像生成和视频预测等领域。目前，已有学者将GAN 模型用于交通流参数估计。GUPTA等[8]提出SocialGAN模型，基于生成对抗网络预测行人轨迹，能够生成更加符合社会规范的行人轨迹，说明GAN 模型也适用于时间序列预测。但该研究仅考虑了行人轨迹之间的时间相关性，没有考虑其空间相关性。ZHANG 等[9]在TrafficGAN模型中考虑交通流时空特征，利用历史交通流数据生成未来交通流数据，但是仅提取了交通流的静态时空特征，无法反映其动态时空特征，且只能进行单步预测。

针对以上研究存在的不足，本文利用门控卷积神经网络提取交通流的动态空间特征，使用基于注意力机制的LSTM 神经网络提取交通流的动态时间特征，基于编码-解码结构进行多步预测，构建基于交通时空生成对抗网络(Traffic Spatio-Temporal Generative Adversarial Network,TSTGAN)的交通流参数估计模型。

1 TSTGAN模型

为描述道路网的交通运行状态，构建表征交通流参数变化的交通流时空矩阵。定义断面n在一段时间内的交通流参数为Fn=[x1,n,x2,n,x3,n,…,xt,n,…,xT,n]，其中，xt,n,t∈{1,2,3,…,T}为时刻t断面n的交通流参数，T为历史交通流数据的时间间隔数。将所有断面的历史交通流参数组合在一起形成交通流时空矩阵F=[F1,F2,F3,…,Fn,…,FN]，n∈{1,2,3,…,N}，其中，N为断面数。

交通流参数估计是指给定T个时间间隔的历史交通流参数，估计第T+1 到T+P时间间隔内的交通流参数，其中，P为交通流数据估计的时间间隔数。由于TSTGAN 模型引入空间模块和时间模块，下面依次介绍空间模块、时间模块和TSTGAN模型的具体结构。

1.1 空间模块

道路网中，某一路段交通运行状态通常受其相邻路段影响，也会被非相邻路段影响。交通流在空间上表现出的这种相互依赖称为交通流的空间特征。由于距离远近的差异，相邻路段上的交通流数据往往高度相关。

车辆在道路上行驶不仅受路段长度和道路宽度等静态固有属性影响，而且受信号控制和交通事件等动态不可控因素影响。因此，空间特征有静态与动态之分。静态空间特征是指由于长度和宽度等静态因素，不同断面交通流数据之间存在潜在的相关性；动态空间特征是指由于拥堵和事故等动态因素，随之改变的交通状况使得不同断面交通流数据之间的相关性发生改变。

淄博市12个交通流量观测断面所处位置及其编号如图1所示。

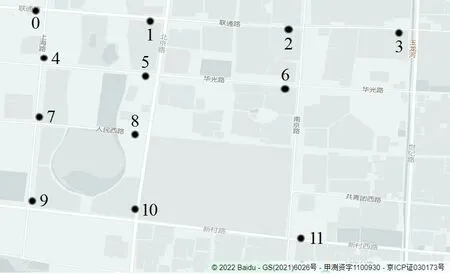
图1 观测断面位置及编号Fig.1 Locations and numbering of observation sections

这些观测断面均位于主干道上相应交叉口的进口道上。以5 min 为时间间隔，统计每个观测断面的交通流量序列。描述这些观测断面在所有时段内两两之间交通流量的皮尔森相关系数矩阵如图2所示。

图2 观测断面交通流量相关系数矩阵Fig.2 Correlation coefficient matrix of traffic volumes obtained from observation sections

由此可见，不同观测断面采集到的交通流量数据具有空间相关性，说明交通流数据具有空间特征。

不同观测断面的交通流量数据不仅整体上具有空间相关性(即静态空间特征)，而且这种空间相关性随着时间推移而发生变化(即动态空间特征)。7:00-9:00、12:00-14:00 和17:00-19:00 这3 个高峰时段内不同观测断面交通流量的皮尔森相关系数矩阵如图3所示。

由图3 可知，不同时段内，各观测断面之间的相关系数表现出明显差异，说明交通状况变化的确影响不同断面交通流数据之间的相关性，也证明确实存在动态空间特征。因此，需要同时提取交通流数据的静态空间特征和动态空间特征。

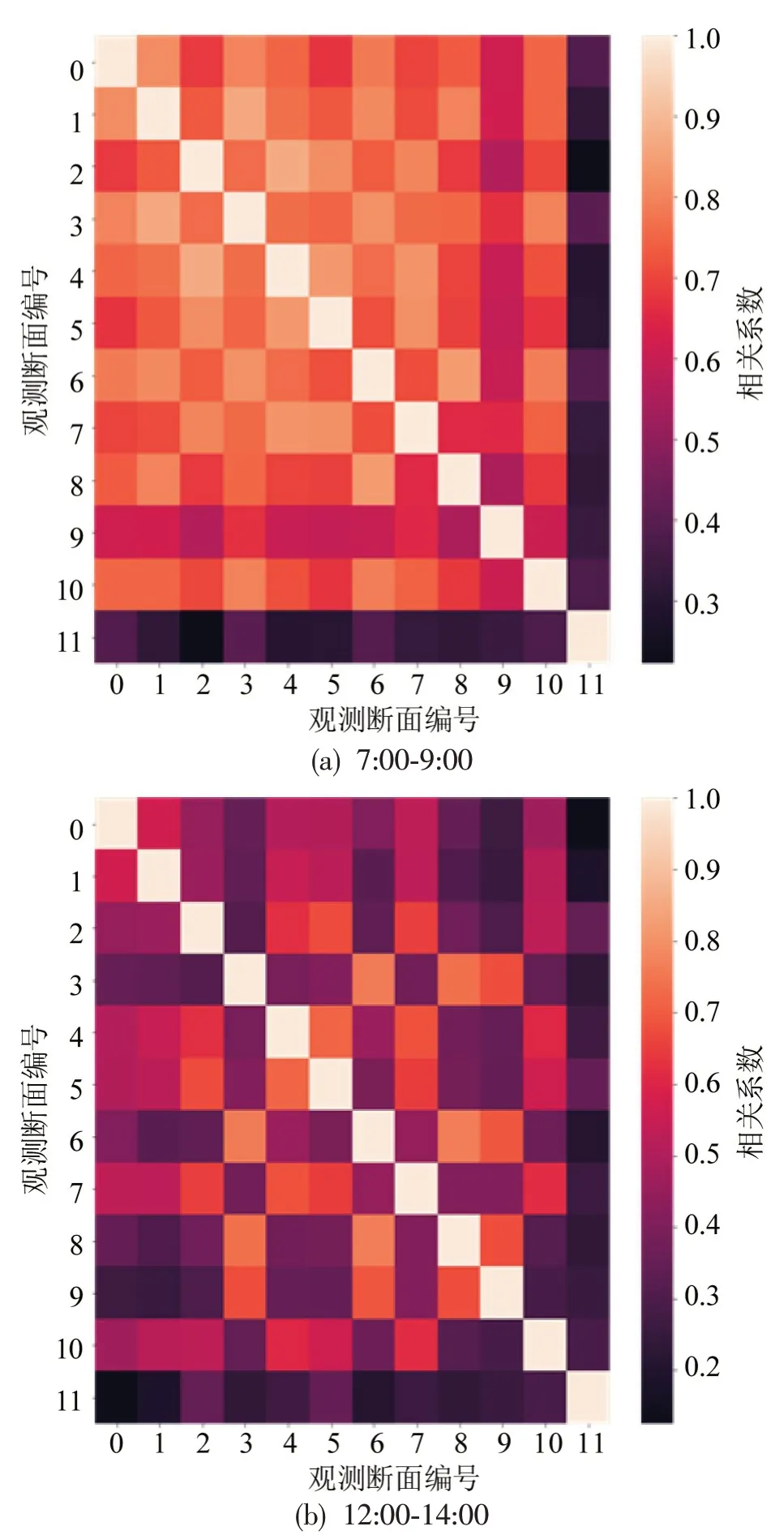
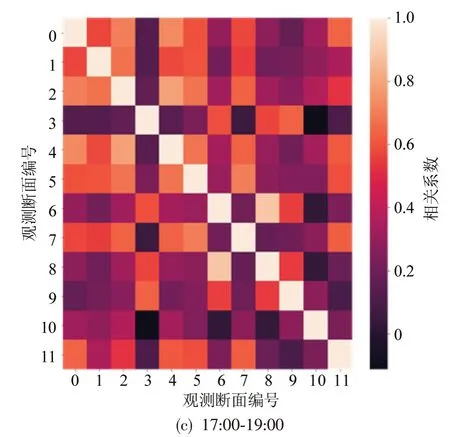
图3 不同高峰时段内观测断面交通流量相关系数矩阵Fig.3 Correlation coefficient matrices of traffic volumes obtained from observation sections during different peak periods

现有研究常利用卷积层提取相邻断面之间的空间特征，但直接利用卷积层提取的是其静态特征，鲜有研究提取其动态特征。

为提取交通流的静态空间特征，将交通流时空矩阵作为初始特征输入卷积层，卷积核在输入特征图上滑动遍历，并进行卷积运算，卷积核大小为1×3，卷积核卷积操作可表达为

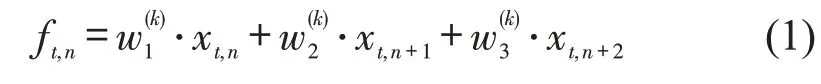
式中：ft,n为时刻t断面n交通流参数的输出值；和分别为卷积核第k层卷积层第1，2，3个权重；xt,n+1和xt,n+2分别为时刻t断面n+1 和n+2 交通流参数的输入值。

当卷积核遍历输入特征图，即可获得交通流参数空间特征的初步表达，即

式中：m=n-2(k-1)。

卷积神经网络如图4所示。设置多个卷积核，可使卷积层提取交通流数据在空间维度上的不同特征，每个卷积核经过卷积操作都会形成一张特征图。同时，为提取不相邻断面之间的空间特征，需要增加卷积层的深度，以便确保提取更加全面的空间特征。

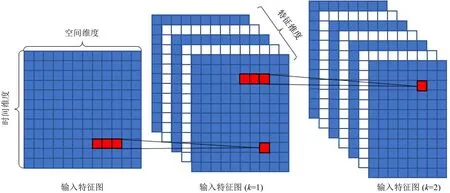
图4 卷积神经网络结构Fig.4 Structure of convolutional neural network

给定初始交通流时空矩阵F(0)，经过k层卷积层，提取的静态空间特征为，即

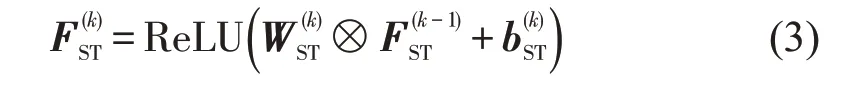
为提取交通流的动态空间特征，引入门控机制[5]学习不同时刻不同区域的交通流特征。门控机制中增加Sigmoid 激活函数，将输入信息映射到[0,1]区间，从而控制信息流出，重点聚焦关键区域对交通流未来发展趋势的影响，保证提取不同交通状况下交通流的空间特征。Sigmoid 激活函数为

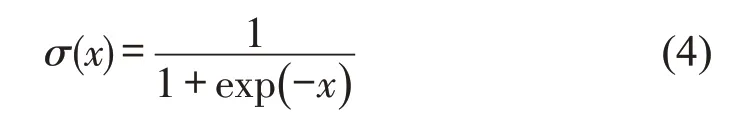
式中：σ(x)为自变量为x的Sigmoid激活函数。

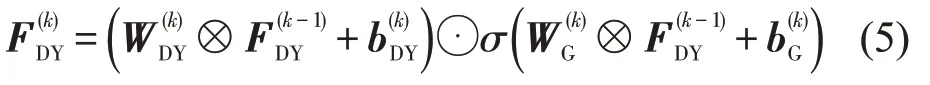
引入门控机制搭建的空间模块如图5所示。最终提取的空间特征FSP为静态空间特征FST与动态空间特征FDY之和，即

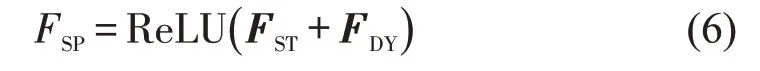
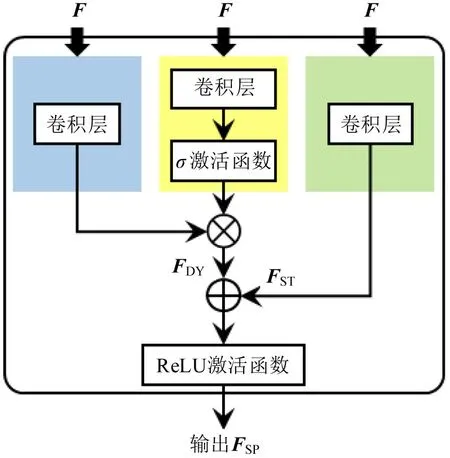
图5 空间模块Fig.5 Spatial block

1.2 时间模块

一个断面的交通流数据通常为时间序列数据，其中，某个时段的数据往往依赖于该时段之前几个时段的数据。交通流在时间上表现出的这种相互依赖称为交通流的时间特征。

LSTM 神经网络增加门结构控制和保护网络状态，解决了传统循环神经网络存在的梯度弥散问题，且缓解了梯度爆炸问题，所以，选择LSTM神经网络捕捉交通流数据的时间特征，将空间模块的输出在空间维度上铺平后的结果FSP=[FSP,1,FSP,2,]FSP,3,…,FSP,t,…,FSP,T作为LSTM 神经网络的输入。LSTM 神经网络包括遗忘门、输入门和输出门，遗忘门将之前的隐藏信息选择性遗忘，输入门将新的信息选择性地输入网络，输出门决定输出信息。遗忘门、输入门和输出门的表达式为

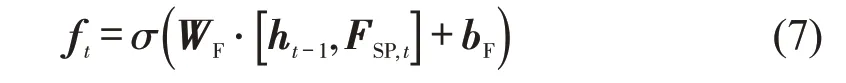
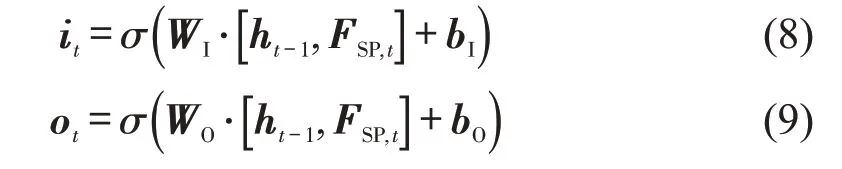
式中：ft、it和ot分别为第t个遗忘门、输入门和输出门的输出向量；WF、WI和WO分别为遗忘门、输入门和输出门的权重；bF、bI和bO分别为遗忘门、输入门和输出门的偏置；ht-1为第t-1 个LSTM单元的隐藏状态向量。

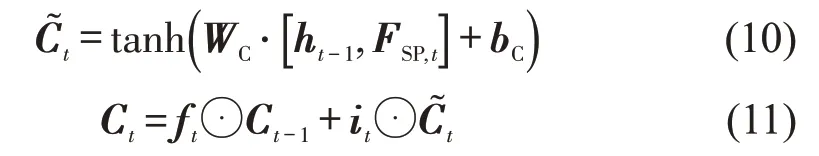
式中：WC、bC分别为备选向量的权重、偏置；tanh为双曲正切函数。

最后，将状态向量Ct经过激活函数处理，再结合输出门的输出ot，得到第t个LSTM单元的隐藏状态向量ht，即

LSTM神经网络第t个LSTM单元的隐藏状态很难表达全部的信息，使得估计误差会随着估计步长的增加而变大，因此，多步估计的效果较差。TSTGAN模型的编码-解码结构如图6所示。

图6 中，基于空间模块与LSTM 神经网络构建编码器；使用LSTM 神经网络构建解码器；将交通网络时空编码信息全部输入解码器。这样，可以有效解决多步估计误差较大的问题。

为更准确地利用编码器每一步的隐藏状态信息，在解码器中加入注意力机制，捕捉交通流数据在时间上的动态变化。交通流参数往往不是线性变化的，不同历史间隔的交通流参数对交通运行状态的影响不同，而注意力机制可很好地提取这种时间特征。注意力描述每个历史时间间隔所得输出对估计交通流数据的贡献程度，通过计算编码器的隐藏状态h与解码器的隐藏状态H之间的相似性，从而确定历史交通运行状态对未来交通运行状态的影响。隐藏状态h与H的相似性分数

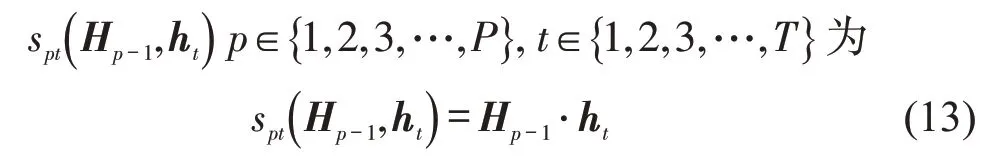
式中：Hp-1为解码器第p-1 个输出序列的隐藏状态；ht为编码器第t个输出序列的隐藏状态。

再将所得相似性分数输入到Softmax函数中为编码器的每个时间步的隐藏状态分配权重，即

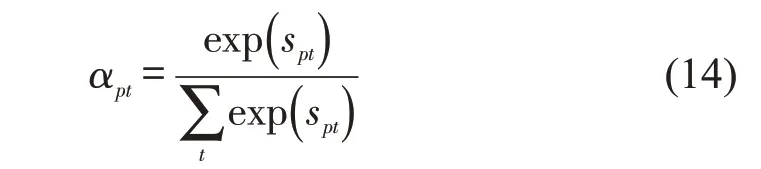
式中：αpt为ht对第p步估计结果的权重。

解码器输出的上下文向量cp为编码器所有时间步的加权和，即

最后，将上下文向量cp经过一层全连接层得到交通流参数估计值，即

1.3 TSTGAN模型

TSTGAN 模型进行交通流参数实时估计的主要思想是将历史交通流时空矩阵输入编码器中生成描述交通运行状态的潜码，再经过解码器生成未来交通流时空矩阵。

编码器与解码器组成生成器，其中，编码器包括空间模块和时间模块。首先，将历史交通流时空矩阵F(0)输入编码器，通过空间模块学习交通流数据的空间特征并在空间维度上铺平得到输出。然后，将FSP输入时间模块，学习交通流数据的时间特征得到输出ht。最后，利用基于注意力机制的编码-解码结构对交通流参数进行多步估计，得到最终的交通流参数估计值。

空间模块、LSTM 层和全连接层组成判别器。先将历史交通流数据F(0)分别与真实的未来交通流数据yp和生成的未来交通流数据结合，得到输入数据，分别输入空间模块，再将学习的空间特征输入LSTM 层，最后经全连接层后得到交通流输出数据YT和YF。

TSTGAN 模型通过判别器判断生成器生成的训练样本的真假，进一步通过生成器与判别器之间的对抗更新模型参数，使得生成器生成更加真实的样本。GAN模型的目标函数为

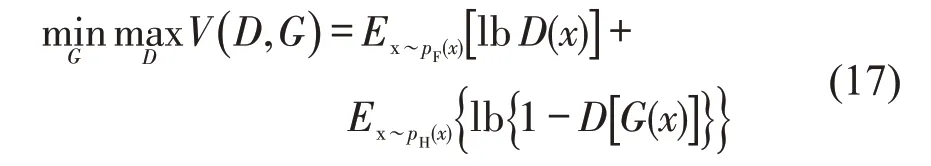
式中：V(D,G)为GAN模型的值函数；G为生成器；D为判别器；x为交通流参数；pF(x)为未来交通流参数分布；pH(x)为历史交通流参数分布；E(·)为变量的数学期望。

TSTGAN模型框架如图7所示。图中，生成器根据历史交通流数据学习交通流数据的概率分布，并生成未来的交通流参数估计值；判别器用来区分真实数据分布的样本DT与生成数据分布的样本DF。给定真实数据分布的样本标签为1，生成数据分布的样本标签为0。训练TSTGAN 模型时，首先，固定生成器，判别器的优化目标是最大化，因此，DT输入判别器的结果接近1(即使D(DT)结果接近1)，而DF输入判别器的结果接近0(即使D[G(DT)]结果接近0)；然后，固定判别器，生成器的优化目标是最小化，此时，生成器使D[G(DT)]接近1。交替训练生成器与判别器，当pF(x)=pH(x)时，训练结果达到全局最优。

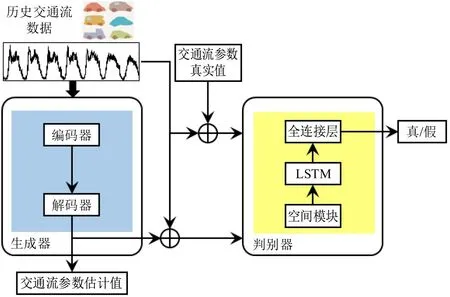
图7 TSTGAN模型框架Fig.7 Framework of TSTGAN model

在GAN模型的损失函数中增加L2损失函数，能提升交通流参数估计的精度[10]。L2 损失函数用来衡量交通流参数的真实值与估计值之间的差异，两者差异越大，损失函数也越大。本文使用的损失函数LT为GAN模型损失函数LG与L2损失函数LM之和，即

2 案例分析

为验证TSTGAN 模型的有效性，使用两个真实交通流量数据集估计交通流参数。第1 个数据集为中国山东省淄博市相邻12个交通卡口2019年4月24日～5月7日2周的过车数据。对这些原始数据进行预处理，将其整理成时间间隔为5 min 的交通流量数据，共计48384 条记录。第2 个数据集为美国加州洛杉矶市西切斯特街区23个线圈检测器2014年5月1日～6月30日2个月的交通流量数据，时间间隔为5 min，共计404064 条记录。将这两个数据集进一步处理为交通流量时空矩阵数据，其中，80%用于模型训练，10%用于模型验证，10%用于模型测试。

2.1 性能指标

均方根误差RMSE(单位为veh·(5 min)-1)可以评价真实数据与所用模型的适应性，平均绝对误差MAE(单位为veh·(5 min)-1)能够很好地反映估计值与真实值之间的误差[11]。RMSE与MAE的值越小，说明模型精度越高，从而说明所用模型较好地提取了交通流数据的时空特征。因此，评价模型性能时，选取RMSE 与MAE 为评价指标，其计算式分别为

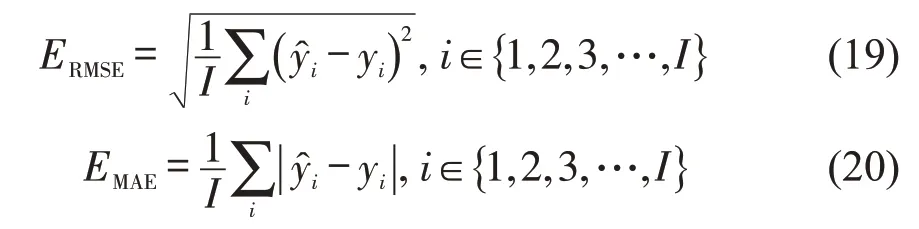
选择历史平均模型(History Average,HA)、支持向量回归模型(Support Vector Regression,SVR)、LSTM、卷积长短期记忆神经网络(Convolution LSTM,ConvLSTM)及时空图卷积神经网络(Spatio-Temporal Graph Convolution Network,STGCN)等现有模型，通过对比说明TSTGAN模型的性能。

HA使用过去同一时刻交通流数据的平均值作为交通流参数估计值。SVR 将历史交通流数据映射到高维度空间，利用线性函数拟合未来交通流数据。LSTM 常用于解决各种时间序列问题。ConvLSTM[4]常被用来解决时空序列问题。STGCN[6]利用图卷积对道路网进行建模。

所建模型采用批量训练，训练批量大小设为64，生成器和判别器的学习率均设为2×10-4，并使用Adam 算法。为保证实验结果的公正，上述所有模型涉及的LSTM 单元的隐藏状态维度均设为128，选取的现有深度学习模型的训练批量大小均设为64，学习率设为1×10-3，且均采用Adam优化算法训练模型。为减少随机性带来的影响，选取5次估计结果的平均值作为最终估计值。

2.2 结果分析

2.2.1 动态时空模块分析

为验证时空模块和生成对抗网络框架的作用，使用淄博市数据集。

选择以下4 个模型进行对比：LSTM 为基准模型，仅捕捉交通流参数的时间特征；TSTGAN_No_Adver 为TSTGAN 模型的生成器部分，训练时不使用对抗方式；TSTGAN_No_L2为相比TSTGAN 模型，损失函数中缺少L2 损失函数；TSTGAN 为本文提出的模型。4 个模型所得的RMSE值和MAE值如图8所示。

图8 各模型RMSE和MAE值Fig.8 RMSE and MAE values obtained from each model

相比LSTM 神经网络，加入了时空模块的TSTGAN_No_Adver 和TSTGAN 模型的误差均降低。随着时间间隔增加，TSTGAN_No_Adver 和TSTGAN模型的RMSE值与MAE值的增加幅度都比LSTM 神经网络小。说明交通流量数据在时空上存在相关性，且TSTGAN 模型的时空模块能很好地提取交通流数据的时空特征。

对比TSTGAN_No_Adver、TSTGAN_No_L2和TSTGAN 这3 种模型，TSTGAN 模型精度最高。表明结合L2 损失函数与对抗方式共同训练生成器，其预测误差比单一使用对抗方式或者L2 损失函数都要低，进一步说明TSTGAN 模型估计结果更加准确。

2.2.2 淄博市数据集实验

使用淄博市数据集，随着时间推移，不断输入历史交通流量数据，在应用中即可实时估计未来交通流量。比较TSTGAN 模型及其对比模型，各模型对未来5，15，30 min 交通流参数的估计性能如表1所示。

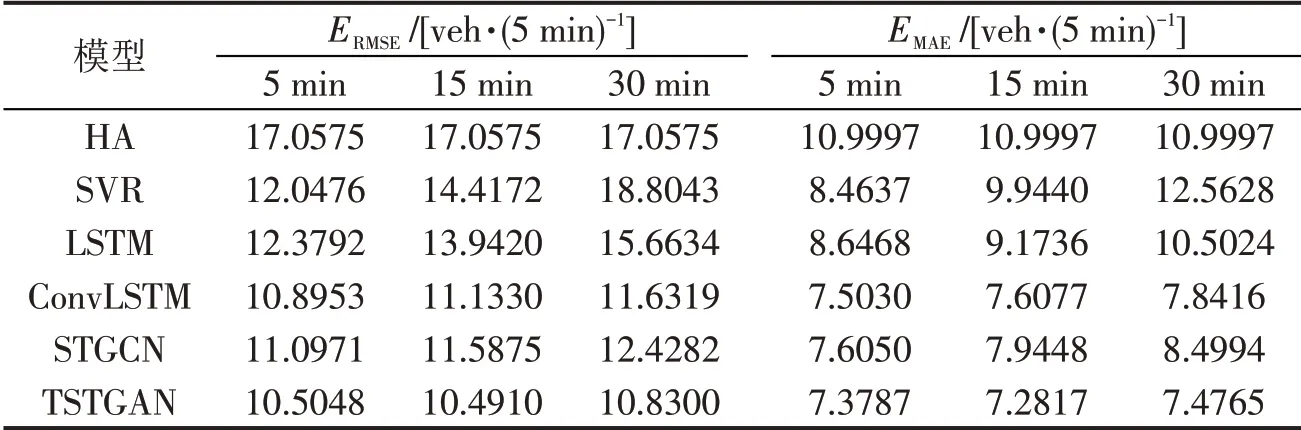
表1 淄博市数据集得到的各模型性能指标Table 1 Performance indices of each model obtained from Zibo dataset

表1 结果表明：相比现有模型，TSTGAN 模型所得RMSE 值分别降低3.58%～38.42%，5.76%～38.50%和6.89%～42.41%；MAE值分别降低1.66%～32.92%，4.28%～33.80%和4.65%～40.49%；随着估计步数增加，所有模型的估计精度都有所下降，但TSTGAN 模型所受影响最小，估计性能下降最慢，从而得到最优的多步估计结果。总之，相比现有模型，TSTGAN 模型估计道路网交通流量时，尤其是多步估计时有最佳的估计性能。

2.2.3 洛杉矶市数据集实验

为验证模型的稳定性，再利用洛杉矶市数据集估计交通流参数。保持超参数不变，分别探究这些模型在工作日与周末交通流参数估计方面的性能，如表2和表3所示。

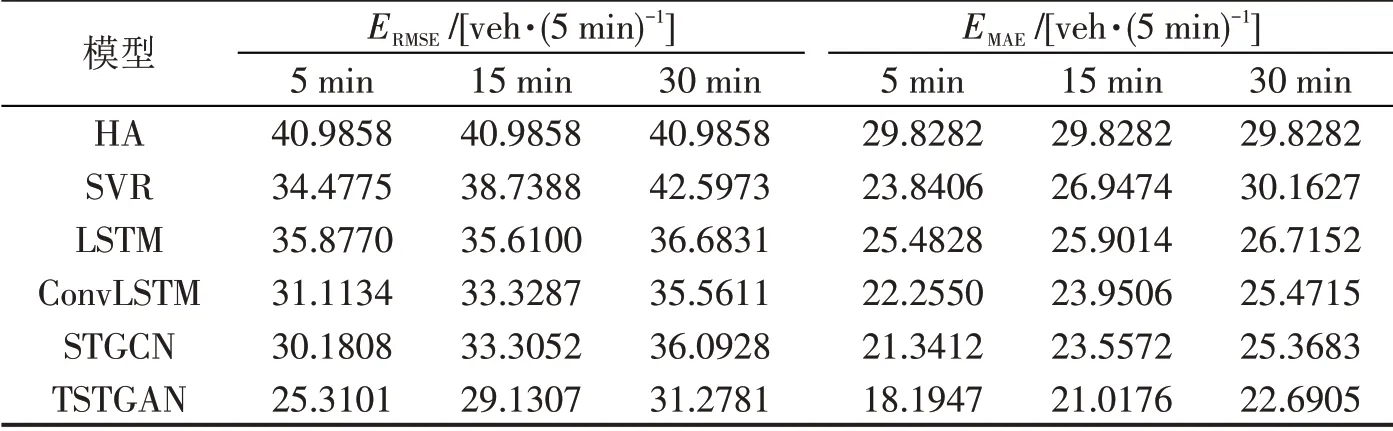
表2 工作日洛杉矶市数据集得到的各模型性能指标Table 2 Performance indices of each model obtained from Los Angeles dataset on weekdays

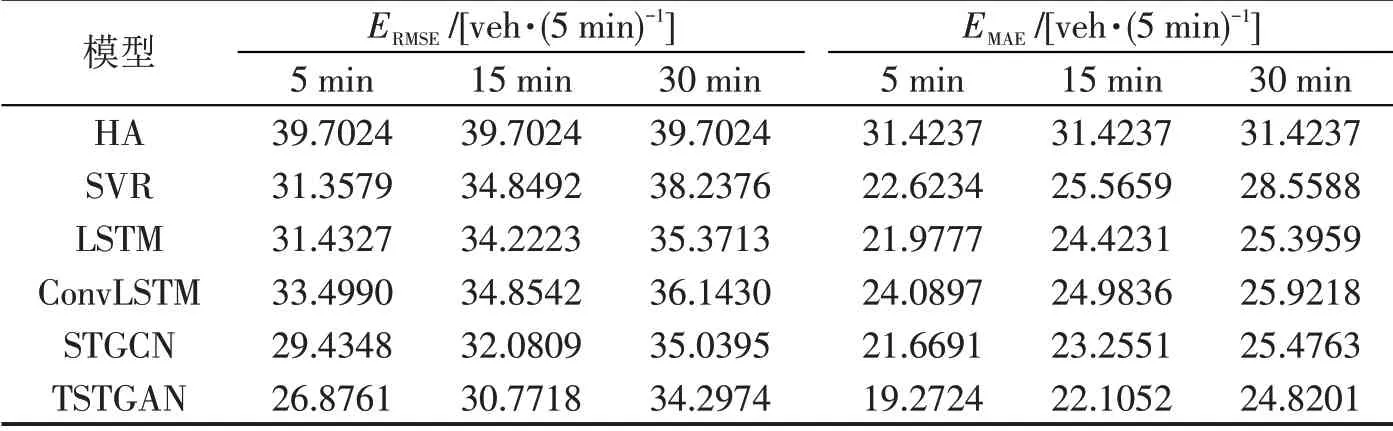
表3 周末洛杉矶市数据集得到的各模型性能指标Table 3 Performance indices of each model obtained from Los Angeles dataset on weekends

无论工作日还是周末，TSTGAN模型的RMSE值与MAE 值均小于现有模型。针对工作日，TSTGAN模型比现有模型的RMSE值和MAE值分别降低12.04%～38.25%和10.56%～39.00%。针对周末，TSTGAN 模型比现有模型的RMSE 值和MAE值分别降低2.12%～32.31%和2.27%～38.67%。相比周末，工作日数据量大，此时，TSTGAN模型的估计精度更高。

尽管洛杉矶市数据集比淄博市数据集涉及的道路断面多，但是，TSTGAN 模型仍然能很好地提取交通流参数的时空特征，对于5，15，30 min 的时间间隔，该模型均取得最优的估计性能。表明TSTGAN 模型估计道路网交通流量时具有较强的普适性。

实际应用中，交通流参数估计所需用时主要受数据读取速度和涉及的断面数影响，断面数本质上是数据量。本文聚焦TSTGAN 模型构建及性能测试，不涉及数据读取速度。使用淄博市和洛杉矶市数据集测试模型性能时，估计交通流量的用时分别为169 ms，219 ms，后者涉及的断面比前者多接近1倍，但用时仅增加50 ms，可见断面数对参数估计用时的影响不大。工程应用中，利用TSTGAN模型估计交通流参数时，配备高性能服务器，采取分布式计算，交通流参数实时估计完全可行。

3 结论

为深入挖掘交通流参数的动态时空特征，基于生成对抗网络构建交通流参数实时估计模型，即TSTGAN模型。本研究主要结论如下：

(1)TSTGAN模型引入时空模块可使RMSE值与MAE 值分别降低15.14%和14.67%以上；TSTGAN 模型利用生成对抗网络训练模型可使RMSE 值与MAE 值分别降低13.03%和11.28%以上；说明TSTGAN 模型能有效提取交通流参数的动态时空特征。

(2)与现有模型相比，估计未来5，15，30 min交通流量，TSTGAN 模型所得RMSE 值和MAE 值分别降低2.12%～42.41%和1.66%～40.49%。

(3)对于交通流参数估计，TSTGAN 模型不仅适用于城市道路场景，同时适用于高速公路场景；当道路断面增多时，TSTGAN模型依然表现出优异的估计性能，说明该模型可以很好地挖掘交通流数据的动态时空特征。