应急车辆动态路径选择的两阶段优化模型

杨枫，种大双

(河南中医药大学，a.管理学院；b.信息技术学院，郑州 450046)

0 引言

随着城市化进程的加快，城市突发事件发生的概率越来越大，给经济生活带来了很多不利影响。因城市内道路交通状况是实时变化的，故在突发事件发生后，必须要考虑应急车辆在路上的行程时间，动态进行路径选择，确保以最短时间对被困人员进行施救。

目前，国内外学者对突发事件发生时复杂路网状况下应急车辆救援速度优化问题展开了大量研究。文献[1]基于水波学原理，建立交通影响等级阈值模型，实现交通影响等级划分，有效提高了应急救援的响应速度。文献[2]提出基于路段行程时间相似性的典型车辆分析方法，比较接近真实的路网状态。文献[3]研究多源交通信息下的动态路径选择模型和算法，提出一种动态网络的先进先出(FIFO)一致性约束准则，实现多源信息下的车辆调度优化。文献[4]引入时间相关的最短路径和车辆路径问题，优化目标为车辆总移动时间最小，为城市道路拥堵问题提出一种解决方案。应急车辆救援速度优化的核心问题是寻找一种最优的动态最短路径算法，目前此类问题的研究相对较少。文献[5]提出面向城市交通网络的具有多项式时间复杂度的K 最短路径(KSP)集合搜索算法，该算法明显优于传统方法。此外，由于车辆路径的行程时间具有显著的不确定性，有少数学者在选择车辆行驶路径时考虑了路径通行可靠性因素。文献[6]以行程时间的可靠性作为路径选择权重，采用Dijkstra 算法求解，可以更准确地反映实际车辆路径选择。

综上，对于应急车辆动态路径选择问题，学者多从车辆整体救援速度或者动态最短路径等角度进行研究，对突发事件下路网状况的复杂性考虑不足。本文充分考虑突发事件带给路网状况的实时变化，以车辆最短行程时间和车辆行驶路径最大可靠性为两阶段优化目标，建立应急车辆动态路径选择的两阶段模型。

1 动态路径选择模型构建

1.1 问题描述

在复杂的城市路网中，应急车辆需要经过多条道路才能到达待救点，如果用路径行程时间表示行驶完该路段所需的时间，那么总行程时间由各个路径行程时间组成。因此，路径选择的目标是从众多路径中选取最优路径，使得总行程时间最短。以路径行程时间为权值，将路网抽象为由节点和边所组成的图G(R,E)，其中，R为节点集合，E为边的集合，i,j为正整数。在任意一个路段中，车的速度是动态变化的，因此行程车速的预测值必须融合时变信息。在调度决策时刻t0之后，如果用行程车速的预测值对车速函数进行拟合，拟合后的结果必然与实际车速函数之间存在偏差，从而导致路段行程时间函数与实际函数之间存在偏差，所求得的最短时间路径不一定是最优路径，因此需要构建动态路径选择模型。

1.2 路段行程时间分析

对于时间段U，假如以Δt为最小时间间隔，将U分割为H个离散时间区间，则U=其中γ=0,1,…,H-1，t0为初始时刻，为最后一个时刻，应急车辆能够在内到达事故节点。事实上，t0时刻的车辆实时路段行程车速可以获得，而时间段U内的其他实时路段行程车速只能与历史车速数据相融合，并进行预测。假设从历史车速数据中取得样本集，选取t0时刻前后几个连续采集周期内的行程车速作为样本向量，该样本集的各子类样本聚集于中心其中，vc(t)表示样本xc中t时刻的路段行程车速，d为样本的维数，φ1、φ2为任意两个正整数。初始时刻t0之后的第φ2个时刻的行程车速可预测为

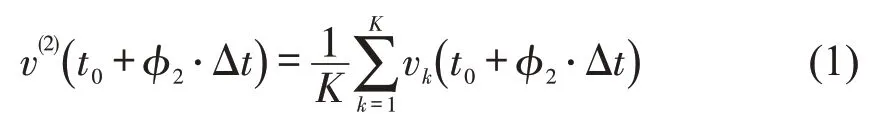
式中：K为最近邻样本集所包含的样本总数，k=1,2,…,K。

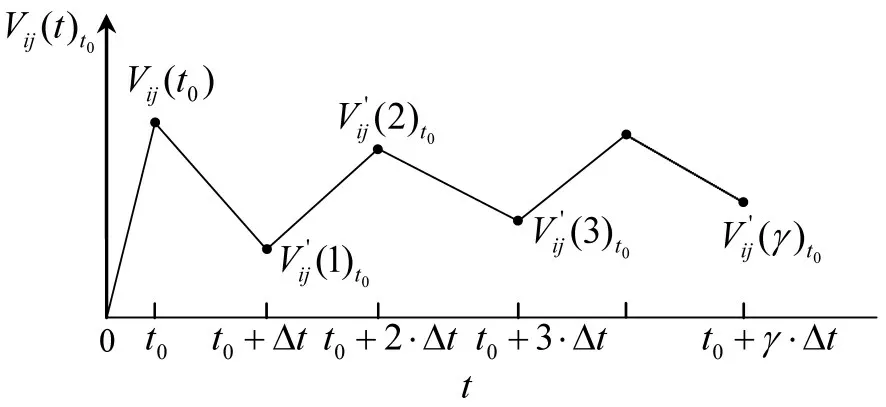
图1 行程车速函数Fig.1 Travel speed function

车速函数为

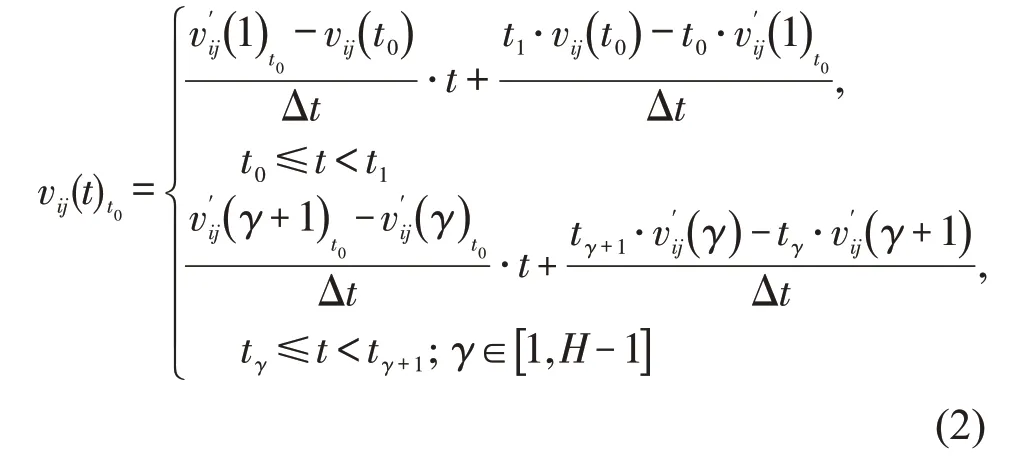
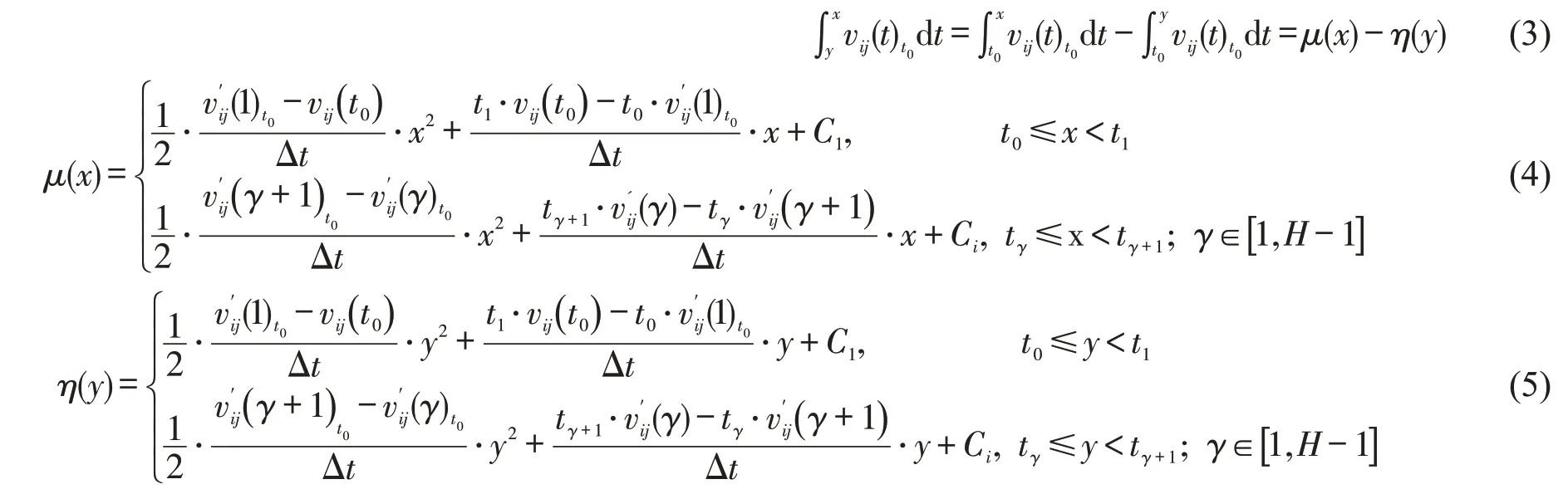
式中：C1，Ci为积分常数，i=2,3,…,H-1，通过原函数的连续性求得。

令式(3)等于路径长度Lij，则应急车辆驶出路段的时间x为

式中：ρ为μ的反函数。可得路段行程时间函数为

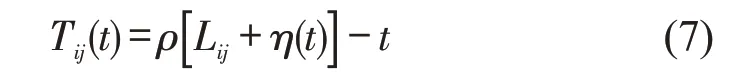
1.3 路径可靠程度分析

在城市突发事件中，城市路网尤其是突发事件区域周边的道路通行必然受到影响，因此在应急车辆路径选择时，需保证路径中某些路段的预计行程时间与实际值发生偏差时，对整体行程时间产生的不利影响最小。本文采用路径可靠度对此进行衡量。

正常情况下，路段(ri,rj)交通流密度是理论正常值，应急车辆处于自由行驶状态时，行程车速接近道路限速值，此时路段行程时间为Tij。对于一条从始发点rs到终点rd的路径，其中，s,d为路网中节点的编号。根据路段行程时间的预测值，应急车辆在ti时刻进入路段(ri,ri+1)，并经过Ti,i+1(ti)后驶出，考虑到应急车辆进入节点ri的实际时间与ti存在偏差，假设实际进入的时间区间为，其中。在此区间内进入时，应急车辆行驶完路段所需的最大行程时间为

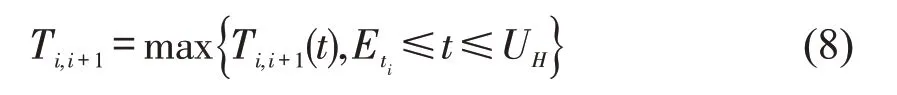
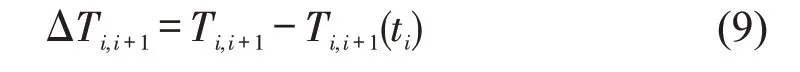
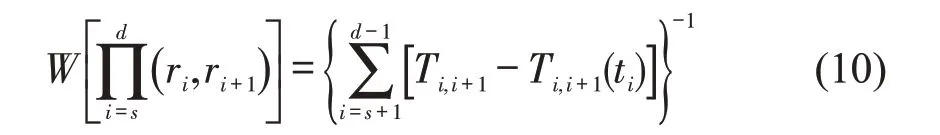
1.4 动态最优路径选择两阶段模型

将城市路网抽象为时间依赖网络模型(R,E,T×U)，其中，R={r1,r2,…,rM} 表示节点集合，相邻节点之间的连接弧为路段(ri,rj)∈E，U为时间区间，Tij(t)为定义在区间U上的路段行程时间函数，表示应急车辆在t时刻进入，从节点ri行驶到节点rj所需的时间，∀t∈U，对于t ＞t0+H·Δt，定义Tij(t)=∞。假设应急车辆位于节点rs，事故所在节点为rd，应急车辆在t0时刻出发，则应急车辆到达事故节点的最优路径为Psd(t0)，最短行程时间为Tsd(t0)。在动态最短路径模型的基础上优化路径可靠度，建立两阶段目标优化模型为

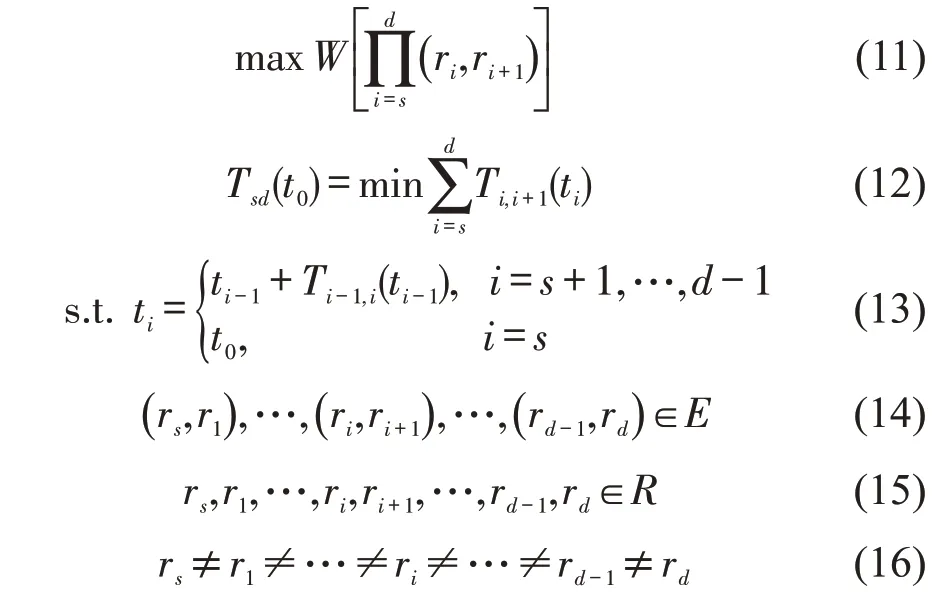
式(11)为路径可靠度目标，使所选路径的可靠度最大。式(12)为路径行程时间目标，由于应急救援的时间紧迫性，优化目标定义为最小化应急车辆行程时间，即应急车辆所经过各个路段的行程时间之和最小。式(13)计算从出发点rs起，应急车辆进入各个路段的时刻ti。式(14)～式(16)为约束条件，保证路径序列是一条没有回路的通路。

2 求解应急车辆动态路径选择问题的混合布谷鸟搜索算法

2.1 混合布谷鸟搜索算法

布谷鸟搜索算法(Cuckoo Search Algorithm，CSA)具有搜索能力强、输入参数少等优点，但其搜索步长为定值，并且布谷鸟莱维(Levy)飞行习性造成长距离步长占比较少，容易陷入局部最优解[7]。本文将蛙跳局部搜索和混沌原理引入到布谷鸟搜索算法中，提出一种混合布谷鸟搜索算法(Hybrid Cuckoo Search Algorithm,HCSA)，首先利用混沌原理进行种群的初始化，使得初始种群具备多样性特征，然后引入蛙跳算法的局部搜索机制来加强局部搜索能力，并在莱维飞行的随机搜索中加入线性递减策略的惯性权重来增强其全局寻优能力。

布谷鸟根据莱维飞行模式选窝产卵，布谷鸟选窝产卵的路线和位置更新公式为

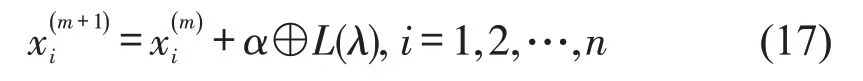
式中：m为迭代次数；为第i个鸟窝在m+1代时的鸟窝位置；⊕为点对点乘法为第i个鸟窝在第m代的鸟窝位置；L(λ)为莱维飞行随机搜索路径；α为常数步长控制量，一般取α=0.01。将L(λ)进行简化处理并经过傅里叶变换得到概率密度函数[8]为

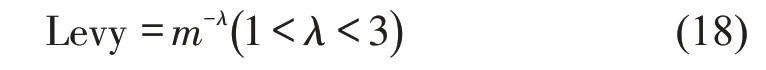
式中：λ为幂次系数。

在进行算法编程时，采用文献[9]中Mantegna提出的模仿莱维飞行的跳跃路线公式，且文献[10]证明了可以采用Mantegna算法实现等价计算。

式中：ζ为莱维飞行的飞行跳跃路线L(λ)；参数β与式(18)中λ的关系为λ=β+1，0＜β ＜2，通常在布谷鸟搜索算法中β=1.5；μ、τ为正态分布随机数，服从的正态分布分别为

μ，τ所对应标准差σμ，στ的取值分别为

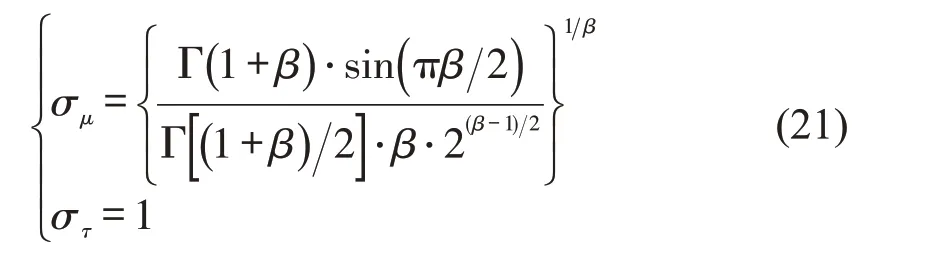
式中：Γ 为标准的Gamma函数。

采用Logistic混沌映射[11]对布谷鸟搜索算法的解进行初始化。Logistic映射来源于动力学系统的人口统计，文献[12]给出的系统方程为

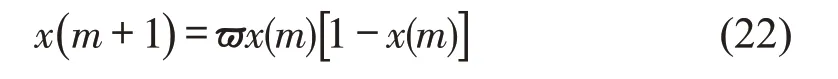
式中：x(m)∈[0,1]；ϖ为控制参数。假如混沌变量的值域为[a,b]，可利用线性变换公式u(k)=a+(b-a)x(m)将混沌变量的值域映射到优化问题的定义域内。

使用蛙跳算法增强局部搜索能力，假如将η个青蛙分成θ个族群，每个族群的青蛙个数为p，那么

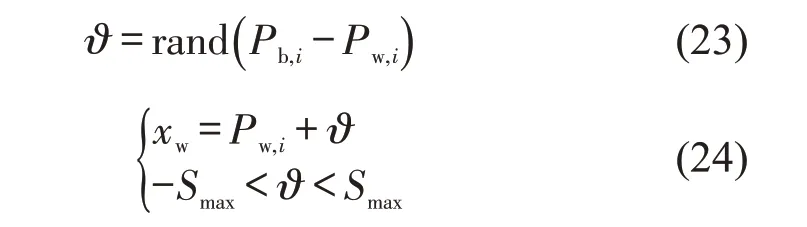
式中：ϑ为青蛙个体的更新矢量；rand 为在(0,1)内随机产生一个数；xw为青蛙的新位置；Smax为青蛙允许跳动的最大步长；Pw,i为第i个族群中最差的青蛙的位置；Pb,i为第i个族群中最好的青蛙的位置。将惯性权重引入布谷鸟寻窝产蛋的路线位置为

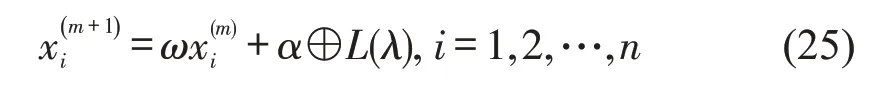
惯性权重ω采用文献[13]提供的一种非线性递减策略，即

两阶段目标优化是从下至上逐层寻优的过程，核心是求解K 条最短路径的混合布谷鸟算法(HCSA-KSP)，如图2所示。

图2 两阶段混合布谷鸟算法原理Fig.2 Principle of two-stage HCSA

2.2 编码方案与适应度函数设计

在混合布谷鸟算法中，每个布谷鸟个体作为路网节点信息的载体，用向量进行表示，每个向量对应于优化问题的一个可行解。编码是从优化问题的决策空间到混合布谷鸟算法搜索空间的一个映射，算法的搜索空间由所有布谷鸟位置向量组合构成，是整型空间的子集。因此，需要根据决策变量的特点将其映射到整型空间。动态最短时间路径模型的决策向量为从应急车辆出发节点rs到事故节点rd的路径选择方案，其中为正整数集合。采用 整数编码方案将路径编码为，则对于包含M个节点的城市路网，可能的编码方案为Md种，此时算法的搜索空间远大于动态路径问题的约束空间，算法容易陷入局部最优，因此需要在整数编码方案中加入路径连通性约束，设计一种新的编码，从而缩小算法的搜索空间。如图3包含17个节点的城市路网中，应急车辆从其所在的节点r14到事故节点r7的一条可行路径为r14→r15-r16→r11→r7，相应的布谷鸟位置编码为Cuckoo:14 15 16 11 7。

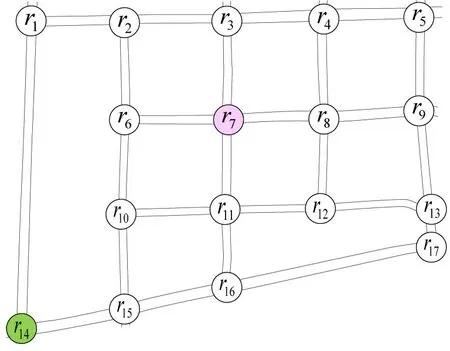
图3 城市路网模型Fig.3 Urban road network model

为保证布谷鸟位置对应的路径序列满足连通性，提出一种随机整数编码方案，具体如下。

定义节点ri的邻接节点集合为，当前路径序列为，假如有集合，从其中随机选择一个节点作为有效节点ri+1，则有

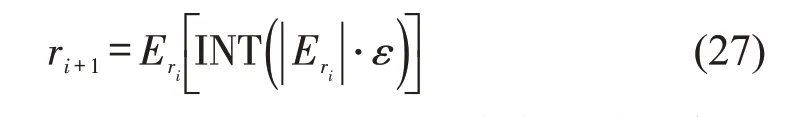
式中：ε为一个随机数，0＜ε ＜1。将当前路径序列更新为，由此逐一搜索至事故点rd，形成布谷鸟的位置编码X=。

适应度是衡量个体优劣的标志，是驱动布谷鸟种群进化的动力。根据动态最优路径模型的第1阶段目标函数，定义HCSA-KSP 算法的适应度函数为

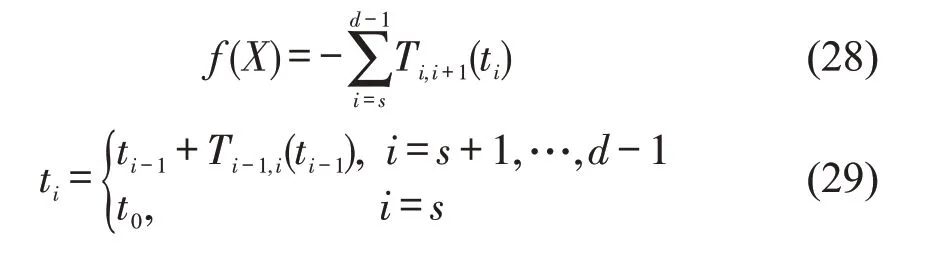
2.3 局部寻优策略

对于满足FIFO 条件的城市路网，必须保证车辆行驶的每一个路段都满足最短时间路径要求，即如果一条最短时间路径经过rq，则一定是从源节点rs到节点rq的最短时间路径。

事实上，每条最短时间路径的子路径也是最短时间路径。由此设计布谷鸟算法的局部寻优策略如下：首先标记最优布谷鸟位置和最差布谷鸟位置中的相同节点；然后从第1 个重合节点起，比较路径与的行程时间与；若，则对于来说，从源节点rs到节点之间，存在1 条时间更短的路径，并将节点标记为瓶颈节点，否则令k=k+1，继续比较和，直到标记出瓶颈节点；最后采用随机编码方案生成1条从节点(标志位)到瓶颈节点的路径，去代替原中的相应路径，由此完成1次对最差布谷鸟位置的更新。

2.4 算法设计

求解动态最优路径的两阶段混合布谷鸟搜索算法以获得K条最优路径为基础，并以路径可靠度为优化目标，最终得到最优路径，HCSA-KSP 算法的步骤如下。

Step 1 初始化种群数量n，搜索维度d，最大迭代次数M，发现概率Pa，搜索空间范围，蛙跳搜索组内更新次数Ne，分组数θ，每组鸟窝的数量p，迭代计数器m=1。

Step 2 混沌初始化种群个体。根据随机编码方案，在决策空间内产生F个布谷鸟个体组成的种群n，产生n维向量，保证每一个布谷鸟编码是一条从应急车辆出发节点rs到事故节点rd的通路，其中，。将Xf的每一维利用式(22)进行更新，产生混沌变量，然后利用载波公式映射到解空间。

Step 3 根据式(12)和式(13)计算F个鸟窝位置对应的适应度值f(Xf)，将所有的鸟窝个体按照适应值降序排列，确定当前最佳鸟窝位置及其适应值。

Step 4 将n个鸟窝分成θ组，每组p个。首先确定族群中最好的解和最差的解，并根据式(23)和式(24)进行更新。如果最差鸟窝位置得到了改善，即，则保留；否则，在该族群内随机产生一个鸟窝位置来替代最差的鸟窝位置。然后对族群重新进行混合，并按照降序排列，构造新的布谷鸟种群，计算新的鸟窝位置对应的适应值，保留最优位置，直到满足局部搜索次数为止。

Step 5 按照式(17)～式(21)，式(25)和式(26)对新的鸟窝位置进行更新，得到1组新的鸟窝位置。

Step 6 随机产生一个均匀分布的数r(0 ≤r≤1)，如果r ＞Pa，则随机改变被发现的概率较大的鸟窝位置，保留被发现概率较小的鸟窝位置，从而获得1组新的鸟窝位置。

Step 8 将各鸟窝位置的适应值进行评估，然后将鸟窝的历史最佳位置进行更新。

Step 9 如果算法满足停止条件，则输出结果；否则，返回Step 3～Step 9继续执行。

3 算例验证

HCSA-KSP 算法是应急车辆动态路径选择的核心，本文以图4所示的某市某区部分区域城市路网为例，选取时间为2021年11月29日8:00-9:00，最短时间间隔Δt=5 min，利用网络爬虫获取交通流数据，交通流数据包括车道宽度、车流密度、路段长度、路段行程时间、实时行程车速和路段预测行程车速，构建实时路段行程车速函数，并求得路段行程时间函数。随机选取10 个节点对，起点为救援车辆出发点，终点为事故发生点。为了模拟城市突发事件发生时的情境，选择正常工作日的上班高峰期时间段作为事故发生后调度时间。考虑复杂的动态路网变化，采用HCSA-KSP算法求解应急车辆出发并到达终点的K条最短路径及其行程时间，并与粒子群算法和经典的布谷鸟算法作对比，验证HCSA-KSP 算法的性能。然后在11月29日～12月3日，每天8:00-9:00 上班早高峰期间，通过秒表计时，按照优化算法求解的动态选择路径，实地驾车获取路径行驶时间。11月29日～12月3日天气情况均为晴间多云和微风状况，8:00-9:00气温在10℃左右，可以认为这几天的外部环境对获取驾驶时间的影响相同，没有太大差异。此外，在车辆起步和停止时刻通过秒表读秒计时，因此时间最小单位设定为秒。HCSA-KSP算法参数如表1所示。

表1 HCSA-KSP算法参数设置Table 1 Parameter selection of HCSA-KSP

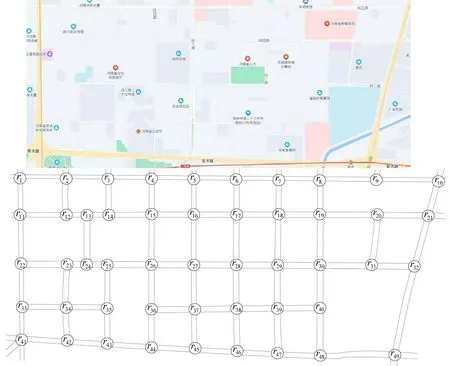
图4 某市某区部分区域地图与路网图Fig.4 Map and road network map of some areas in a district of a city

为求得10 个节点之间的K 条最短路径及其行程时间，运行HCSA-KSP 算法、粒子群算法和经典布谷鸟算法，获得的计算结果如表2所示。

分析表2最短路径选择结果可知，HCSA-KSP、PSO-KSP和CSA-KSP算法都能得到节点间的K条最短路径及其行程时间，与实地驾车获取的路径行驶时间相比，各算法求解的结果误差最大的为7.7%。

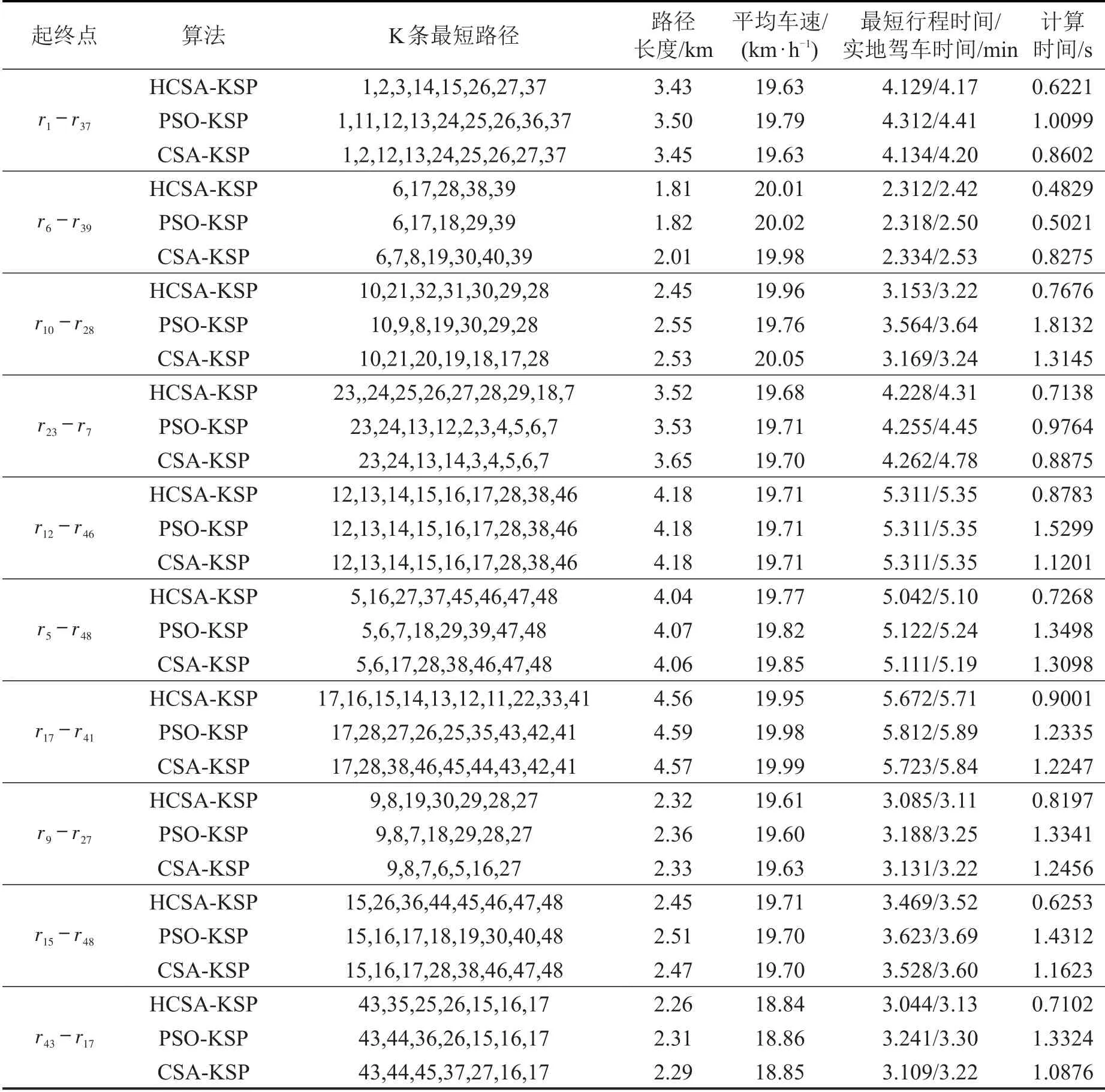
表2 K条最短路径选择结果Table 2 Results of K shortest paths selection

以节点r1到节点r37和节点r12到节点r46的路径寻优为例，HCSA-KSP算法与粒子群算法和经典布谷鸟算法的收敛过程如图5所示。从图5可以看出，选择节点r1到节点r37时，HCSA-KSP算法得到的行程时间在算法迭代到约18 代时达到全局收敛，而PSO-KSP 算法约在49 代时收敛，CSA-KSP算法约在71 代时收敛，HCSA-KSP 算法和CSAKSP 算法比PSO-KSP 算法得到更少的行程时间。选择节点r12到节点r46时，HCSA-KSP 算法同样比PSO-KSP 算法和CSA-KSP 算法收敛的要快，但是三者获得相同的行程时间。

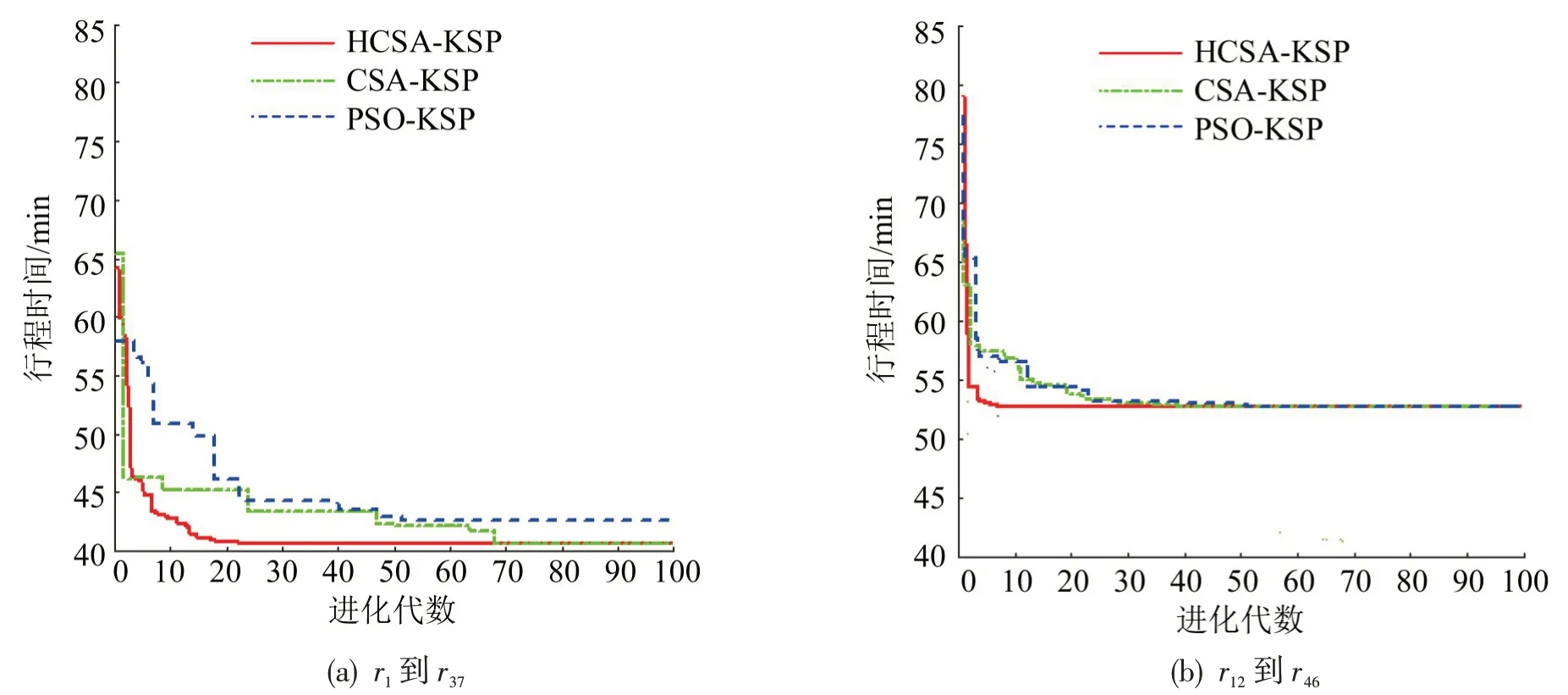
图5 r1 到r37 和r12 到r46 路径寻优的3个算法进化过程Fig.5 Evolutionary processes of three algorithms in path optimization of r1 to r37 and r12 to r46

总体来讲，对于相同的起点和终点，由于不同算法计算得到的最优路径不同。相比之下，HCSAKSP算法获得的路径最短行程时间要更优，且算法的计算时间更短，算法能够更快地收敛到最优解。说明HCSA-KSP 算法解决应急车辆动态路径选择问题相比其他算法性能更优。

4 结论

城市路网的交通状况是实时变化的，突发事件发生后救援车辆除了要考虑以最短的时间到达待救点之外，还必须考虑路网实时状况。为此，本文创新性地提出以最大路径可靠度为第1 阶段优化目标，以最短行程时间为第2阶段目标的两阶段优化模型。此外，本文设计了一种混合布谷鸟搜索算法，通过混沌搜索改进了布谷鸟算法的初始种群，并通过加入蛙跳算法改进了局部搜索能力，通过加入路径连通性约束的编码机制，缩小了算法的搜索空间。以某市某区部分路网为例，将实时交通数据应用到模型和求解算法中得到的结果与实地驾车获取的结果相比，误差较小。本文提出的两阶段优化模型成功获得了应急车辆的动态行驶路径，得到了最优的结果。本文仅选取了部分路网为研究实例，全路网多事故情境下研究将是未来的方向。