两参数指数分布的位置参数区间估计研究★

徐亚茹，徐晓岭，顾蓓青

（上海对外经贸大学统计与信息学院，上海 201620）

0 引言

两参数指数分布是可靠性统计中非常重要的寿命分布模型之一，其在工兵器械、航天航空、生物医学和医疗保险等领域中有着广泛的应用。

设总体X服从位置参数为μ、刻度参数为θ的两参数指数分布exp（μ，θ），其分布函数F（x）和密度函数f（x）分别为：

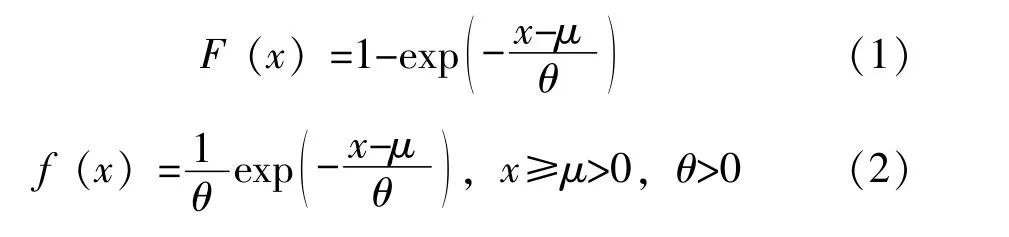
关于两参数指数分布总体位置参数区间估计问题有很多学者做过研究。费鹤良、戴树森等在文献[1-2]、王黎明在文献[3]中构造的枢轴量服从F（2，2n-2）。而N.R.Mann在文献[4]中构造的枢轴量服从F[2k，2（n-k）]，其中k=[n/2]。事实上，针对F[2k，2（n-k）]，其k可以取1，2，…，n-1，也就是说文献[1-4]没有解释为什么k取1或取[n/2]。

本文针对枢轴量的分布服从F（2k，2（nk）），k=1，2，…，n-1，通过1 000次Monte Carlo模拟考察位置参数区间估计的可靠度与精度，发现k=1较优。同时通过构造另一服从χ2[2（n-1）]的枢轴量也进行1 000次模拟比较，也发现k=1较优。论文还通过似然比检验的方法从理论上说明k=1的优良性。

1 求位置参数区间估计的枢轴量的构造

首先，给出3个引理，其中引理1与引理2由文献[5]得到，引理3由文献[6]得到。

1.1 通过F分布构造求位置参数μ区间估计的枢轴量

给定参数真值θ=1，μ=1，10，20，50，样本容量n=10，20，通过1 000次Monte Carlo模拟，统计上述5种情形满足的次数，结果如表1所示，从中可以发现：1）只有k=1时，全部满足情形一，也就是说情形二——五不可能出现；2）对于2≤k≤n-1，情形二——五都有可能发生，尤其是当μ真值较小、k值接近n时，很少满足情形一，也就是得不到位置参数μ的区间估计；3）为得到位置参数μ的区间估计，推荐使用枢轴量G1（μ）。

表1 位置参数μ区间估计满足各种情形次数统计表

续表1 位置参数μ区间估计满足各种情形次数统计表

续表1 位置参数μ区间估计满足各种情形次数统计表

1.2 通过χ2分布构造求位置参数μ区间估计的枢轴量

给定参数真值θ=1，μ=1，10，20，50，样本容量n=10，20，通过1 000次Monte Carlo模拟，统计情形六和情形七满足的次数，结果如表1所示，从表1中可以发现：1）当μ的真值很小时，也就是说样本数据较小时，情形七有可能发生，只时发生的次数很少；2）当μ的真值较大时，即样本数据较大时，情形七几乎不发生，此时用χ2分布构造枢轴量求位置参数μ区间估计的方法是可行的。

1.3 位置参数μ区间估计的模拟比较分析

取参数真值θ=1，μ=1，样本容量10，20，置信水平1-α=0.9，通过1 000次Monte Carlo模拟（即对枢轴量Gk（μ），k=1，2，…，n-1都满足情形一1 000次及枢轴量T（μ）也都满足情形六1 000次）分别计算利用枢轴量Gk（μ），k=1，2，…，n-1，以及T（μ）所得到的1 000个区间估计当中包含参数真值的次数、区间估计的平均下限、上限和平均长度，结果如表2所示，从表2中可以看到：1）固定样本量n=10，只有利用枢轴量Gk（μ），k=1，2，3，4所得到的区间估计包含真值的次数可以达到900次以上；样本量n=20，只有利用枢轴量Gk（μ），k=1，2，…，12所得到的区间估计包含真值的次数可以达到900次以上，也就是说，随着k的增大区间估计包含真值的次数逐渐地减少；利用枢轴量T（μ）所得到的区间估计包含真值的次数都在1 000次左右；2）枢轴量G1（μ）得到的区间估计的平均长度要比枢轴量T（μ）所得到的要小，所以推荐使用枢轴量G1（μ）；3）随着k，2≤k≤n-1的不断增大，所得到的区间估计包含真值的次数越来越少，与900次相差较大，且区间估计的平均长度越大，所以使用枢轴量Gk（μ），2≤k≤n-1求位置参数μ的区间估计是不合适的。

表2 位置参数μ区间估计的模拟比较

1.4 似然比检验分析

根据N-P基本引理，对于简单的假设检验问题，最优检验一般选择似然比检验，并且极大似然比的分布并不取决于位置参数和尺度参数的值，所以本文从似然比检验的角度来研究k取何值时，位置参数μ区间估计最优。

设X1，X2，…，Xn来自总体X~exp（μ，θ）的容量为n的一个样本，其次序统计量记为X（1），X（2），…，X（n），考虑假设检验问题为：

若D>Fα[2，2（n-1）]，则拒绝原假设H0，所以在似然比检验中可以看出所构造出的统计量与位置参数和尺度参数无关，并且恰好服从F[2，2（n-1）]，恰好是F[2k，2（n-k）]，k=1的情形。此时，利用枢轴量G1（μ）（其服从F[2，2（n-1）]）所得到的区间估计较优。

2 模拟算例及实例分析

a）例1

取参数真值为θ=1，μ=20，置信水平1-α=0.9，生成一组样本容量n=10的数据为：20.035 3，20.037 9，20.119 1，20.649 8，20.695 1，20.775 1，20.842 8，21.040 8，21.331 5，23.582 7。

分别计算利用枢轴量Gk（μ），k=1，2，…，n-1以及T（μ）统计满足7种情形的次数，结果如表3所示，只有k=1，2，3满足情形一X（1）），T（μ）满足情形六。利用枢轴量Gk（μ），k=1，2，3和T（μ）得到的区间估计的下限、上限和长度，结果如表4所示，所得到的区间估计下限和上限满足情形一，并且枢轴量G1（μ）得到的区间估计最优。

表3 位置参数μ区间估计满足各种情形的统计表

表4 位置参数μ区间估计的比较

b）例2[7]

20名白血病患者接受同一药物治疗直到缓解的有序时间（Lawless，2003）是：

本文选取20名白血病患者接受同一药物治疗直到缓解的时间数据，通过表5的数据可以看出，4种不同的拟合检验方法在同一显著水平（α=0.1）下的P值均大于0.1，不拒绝原假设H0：F（x）=exp（μ，θ），也就是说这组数据被认为服从两参数指数分布。

表5 拟合检验表

分别计算利用枢轴量Gk（μ），k=1，2，…，n-1以及T（μ）判断该组数据是否满足情形一和情形六，结果如表6所示，从表6中可以看出：1）只有k=1，2满足情形一可以得到μ区间估计为

表6 位置参数μ区间估计满足各种情形的统计表

表7 血病患者药物治疗到缓解时间μ的区间估计

3 结束语

本文构造服从F[2k，2（n-k）]和χ2[2（n-1）]的枢轴量，用Monte Carlo模拟考察区间估计的精度，得到利用服从F[2，2（n-1）]的枢轴量的方法最优，并且从似然比检验的方法解释说明了k=1最好；从算例和实际例子结果分析来看，使用构造枢轴量服从F[2k，2（n-k）]的方法中，在k=1时满足情形一不会出现和的区间倒挂现象，区间估计长度最短，性能较为稳定，进一步地解释说明了很多文献在用传统方法计算区间估计选择构造枢轴量F[2，2（n-1）]的原因。