砂-粘-粉互层地层明挖隧道沉降特征分析及预测

邓志强，罗会武,3，张瑞元,3，喻成成，陈培帅

(1.中交第二航务工程局有限公司，湖北 武汉 430040； 2.中交公路长大桥建设国家工程研究中心有限公司，北京 100088； 3.交通运输行业交通基础设施智能制造技术研发中心，湖北 武汉 430040)

隧道沉降是工程的控制性指标，也一直是工程领域研究的热点问题，但沉降不仅受地基土体自身非线性的影响，也受到外部荷载变化控制[1]，具有明显的非线性特征。高速铁路沿线隧道沉降量及沉降特征是影响铁路建设的关键性指标，分析沿线各断面的沉降特征，探索其差异性原因，对沉降控制做到有的放矢，对各断面最终沉降量进行预测，为施工决策提供极大便利。

针对隧道沉降差异性及预测问题，王婷等[2]在分析郑西客运专线试验段路基沉降实测资料的基础上，认为由于施工期的隧道受外部荷载影响较为明显，沉降曲线不能表现出稳定的自有规律性和特定的线型。王敏等[3-4]基于沪宁城际高速铁路运营3a的监测数据，认为工后沉降与当量软土厚度呈正相关，且由于动载造成的工后沉降较小。刘国彬等[5-6]依托上海地区地铁盾构隧道沉降监测数据，分析了地铁隧道长期沉降的原因，指出地下水开采是上海地铁沉降的主要原因。黄广龙等[7]基于长期观测数据，对南京地铁一号隧道沉降特征及原因进行研究，明确了可能导致隧道沉降变形四个因素：降水因素、堆载因素、施工因素和地质因素，但没有明确各因素之间的关联及对地铁沉降造成的影响。基于实测数据的沉降曲线拟合法，在预测工程最终沉降量方面具有很大优势。常用的曲线拟合方法有Asaoka法[8]、双曲线法[9]和三点法[10]等，潘林有等[11]对其在工程中的应用作了详细介绍。曲线拟合方法在工程界运用广泛，但针对施工期，数据积累时间较短情况的预测方法选用方面存在一些疑惑。

针对上述问题，本文基于机场2号隧道施工期沉降监测数据，统计分析各断面沉降特点，分析沉降差异性原因，运用曲线拟合的方法对隧道最终沉降量进行预测，并对其精度进行分析，不仅对机场2号隧道的安全运营提供了极大帮助，也能为类似的工程提供借鉴。

1 工程概况

京雄城际铁路机场2号隧道，全长7.2 km，起讫桩号为DK46+092～DK53+300，最大埋深为28.64 m。采用单洞双线设计，线间距5 m，柱式洞门结构，路线主要区段主体结构断面形式为拱形明洞结构，明挖法施工，根据基坑支护形式的不同分为放坡开挖与钻孔灌注桩组合的形式。线路穿越天堂河、永定河两条河流，下穿永定河段起讫桩号为DK50+980～DK52+802，在河道管理范围内长度为1 822 m(沿机场2号隧道线路方向量测)，与永定河中心线交叉角度75°。

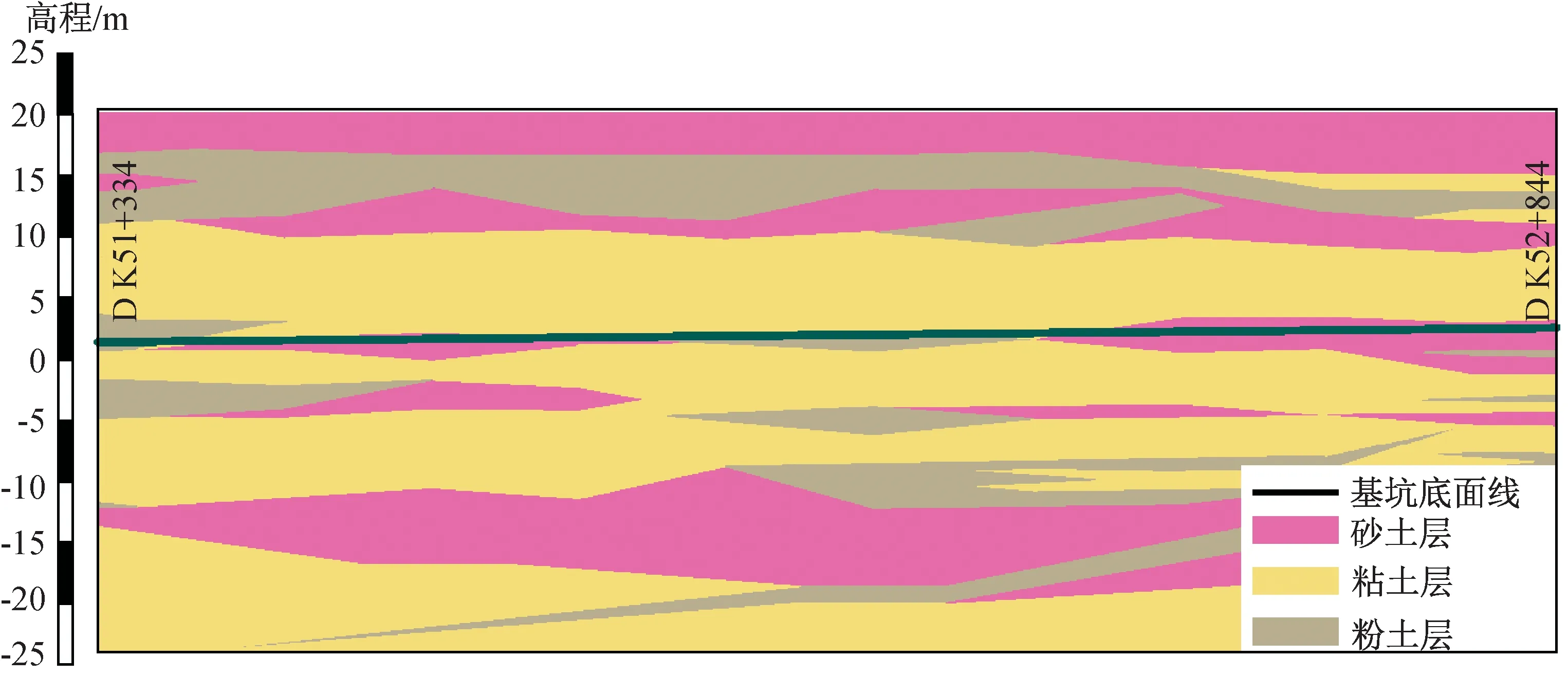
图1 隧址区代表性地层剖面Fig.1 Representative stratum section of the tunnel site

2 沉降监测与特征分析

2.1 隧道沉降监测点布置

按照《铁路隧道工程施工安全技术规程》(TB 10304—2020)[12]的要求进行仰拱沉降监测，监测仪器采用精密水准仪(EL302 A)和钢尺配合使用，对于不方便地段采用高精度全站仪(Leica TS06)进行量测。监测断面根据基坑深度、隧道地基土体性质及埋置深度等选取。每个断面布置3个监测点，分别位于隧道仰拱的左、中和右侧，如图2所示。各断面隧道仰拱施工完毕形成强度后，立即进行沉降监测，监测频率为3～5次/月，经数据分析确认达到基本稳定后，1次/月。

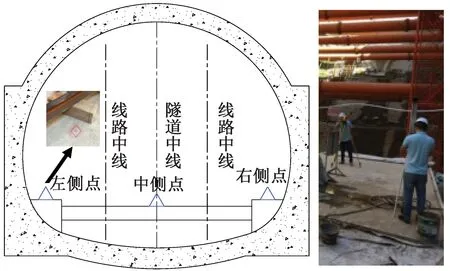
图2 现场监测点分布Fig.2 Arrangement of actual monitoring points

2.2 隧道沉降特征

对全线128个断面沉降监测数据进行整理分析，发现隧道沉降曲线可分为类双曲线型(39个)、U型(46个)和振荡型三类(43个)。

2.2.1 类双曲线型沉降曲线

类双曲线型沉降曲线特征是：沉降初始发展较快，沉降较大，随着隧道施工的推进，沉降逐渐稳定，沉降速率逐渐减小并趋近于零，曲线发展趋于平缓，虽然曲线中部存在一些异常上升的点，但曲线整体符合双曲线特征，如图3所示。地基沉降稳定周期长，约6个月。

图3 类双曲线型沉降曲线Fig.3 Hyperbolic-like settlement curve

2.2.2 U型沉降曲线

U型沉降曲线特征是：沉降初始发展极快，在短时间内(2个月)迅速完成沉降，随后沉降速率逐渐减小并趋近于零，沉降逐渐稳定，曲线发展趋于平缓。但随着隧道建设的推进，隧道出现抬升的现象，且抬升幅度较大，达最大沉降值的70%，曲线整体呈现两头高、中间低，如图4所示。

图4 U型沉降曲线Fig.4 U-shaped settlement curve

2.2.3 振荡型沉降曲线

振荡型沉降曲线的特征是：沉降发展较平稳，隧道始终在初始位置上下波动，且随着时间推移，波动幅度呈现扩大的趋势，曲线整体表现为在初始位置来回振荡形式，如图5所示。

图5 振荡型沉降曲线Fig.5 Oscillating settlement curve

3 沉降特征差异性原因分析

隧道沉降受多方面因素影响，如回填与开挖量差异、隧址区的地质条件、地下水位的变化等。同一断面的沉降同时受到不同的因素相互作用，对其沉降曲线特征变化均有贡献。

3.1 回填深度占比

采用明挖法施工，隧道线路开挖量远大于回填量，线路各段回填深度占比见表1，各段回填深度占比均值为34%，回填量较小，地基土体整体处于超固结状态。粘性土由于卸压，出现回弹现象，随着填土荷载的施加，沉降开始发生，此时的沉降为回弹再压缩沉降。无粘性土基本无回弹，隧道沉降量较小，特别是振荡型沉降断面，隧道沉降量的波动范围为±3 mm。回填深度的大小与隧道所受到的上部荷载具有直接关系。

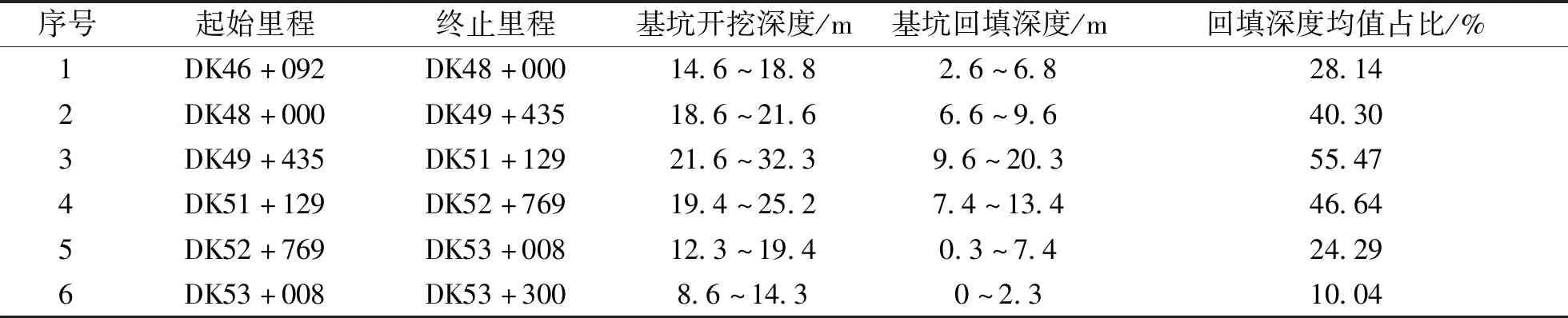
表1 各段回填深度与开挖深度比值Tab.1 Ratio of backfill depth to excavation depth

3.2 地下水位

线路原始地下水位均高于开挖深度，且工程施工完毕后，原处于干涸状态的永定河人工回灌，河道附近地基土体内地下水位有较大的上升，引起隧道出现明显的抬升现象，如图6所示。地层中砂-粘-粉互层现象严重，地层透水性与黏土含量有较大关系，黏土含量越少，地层透水性越好，地下水产生的浮力越大，隧道受地下水位影响越严重，反之地下水位对隧道沉降影响越小[13]。地下水位与隧道振荡现象有直接关系，地下水是使隧道抬升的主导性因素。

图6 断面地下水位升高，隧道抬升Fig.6 The groundwater level rises and the tunnel rises

3.3 主要压缩层土体性质

据《北京地区建筑地基基础勘察设计规范》(DBJ 11—501—2009)[14]中SGR0.5b的概念，地基的主要压缩层是指在基础底面以下相当于0.5倍基础底面宽度深度范围，本项目隧道宽15 m，主要压缩层厚度为隧道底部以下7.5 m范围。

分类统计三种沉降特征断面的主要压缩层土层性质，如图7—图9所示。类双曲线型沉降断面主要压缩层中砂土和粉土占比较小，黏土占比较大，普遍超过60%，甚至存在主要压缩层全部为黏土的断面(图7)；U型沉降断面主要压缩层中砂土和粉土占比之和与黏土的占比相当，也存在个别断面主要压缩层全部为黏土的现象(图8)；振荡型沉降断面主要压缩层中砂土和粉土占比较大超过60%，甚至有个别断面主要压缩层全部为砂土(图9)。

图7 类双曲线型沉降曲线断面土体类型分布Fig.7 Distribution of Soil Types in the Section of a Hyperbolic-like Settlement Curve

图8 U型沉降曲线断面土体类型分布Fig.8 Distribution of soil types in U-shaped settlement curve section

对三种沉降特征断面主要压缩层土体性质汇总，如图10所示，可以发现沉降曲线的形态与基础下部主要压缩层土性存在直接对应关系，无粘性土(砂土+粉土)含量越高，沉降曲线振荡越明显，反之，沉降曲线越接近类双曲线型。经典的Biot固结理论[15]，黏土沉降以固结沉降为主，土体固结周期长，沉降曲线符合双曲线特征，主要压缩层中黏土含量越高，固结沉降所占的比重越大，沉降稳定的周期越长，在沉降监测曲线上表现为类双曲线型。无粘性土沉降主要以瞬时沉降为主[16]，短时间内沉降达到稳定，随着主要压缩层中砂土和粉土含量增加，沉降初期发展较快，且迅速达到稳定，由于地层中无粘性土含量较高，透水性较好，永定河回灌后地下水位上升，隧道受浮力作用向上抬动，沉降曲线末端向上翘起，形成U型。随着无粘性土在地层中的含量进一步增加，地基沉降主要表现为瞬时沉降，且由于地基土体处于超固结状态，地基沉降并未进一步发展，而是随着地下水位的变化在初始位置上下波动，在沉降监测曲线上表现为围绕初始位置上下振荡。

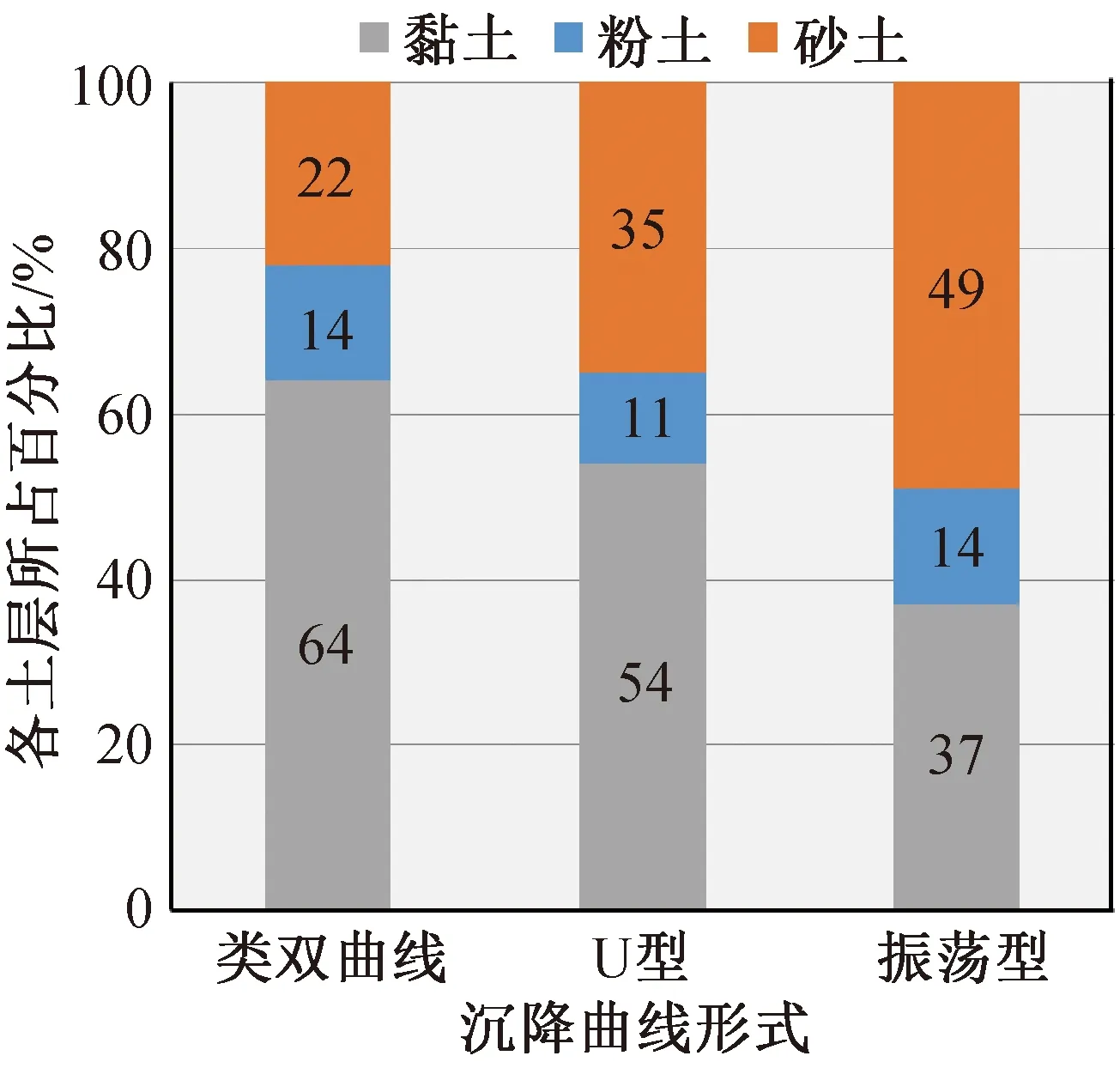
图10 不同沉降曲线土层性质分布Fig.10 Distribution of soil layer of each settlement curve

3.4 沉降特征差异性原因讨论

回填比例、地下水位高度和主要压缩层土体性质是控制隧道沉降的主要因素。回填深度与隧道上部荷载正相关，地下水位高度决定隧道所受初始水头高度，主要压缩层土体性质控制隧道所受浮力大小，三者结合，组成隧道的受力体系，控制隧道沉降。其中粘土含量不仅决定土层透水性，也影响着地基土体回弹再压缩，进而影响回弹压缩变形量。如图11所示，统计各里程主要压缩层粘性土含量，并将其与该断面沉降值综合分析，可以发现主要压缩层粘性土含量越高，沉降值越大，二者成正相关。

图11 各里程沉降值与粘土含量关系Fig.11 The relationship between the settlement value of each mileage and the clay content

4 沉降预测及精度分析

4.1 沉降预测方法

4.1.1 Asaoka法

针对一维固结问题，Asaoka认为可以通过一个级数形式的普通微分方程[8]近似的表示为

(1)

式中：S为总固结沉降量，a1、a2、···、an、b取决于固结参数和地基情况的常数。对于工程而言，式(1)采用一阶微分项，其余项均为高阶无穷小可以忽略。将时间t离散为等间距的时间段Δt，取每个时间段的端点时间tj对应的沉降量为Stj，即：

Stj+Δt=β0+β1Stj

(2)

式中：Stj、Stj+Δt分别对应为tj、(tj+Δt)时的沉降量，β0为沉降值，β1为无量纲的常量。对满载后的一系列三点(Stj、Stj+Δt)按式(2)进行线性拟合，求得参数β0、β1后，计算地基的总沉降量为

(3)

预测步骤：(1)读取数据，选择实测沉降曲线的恒载阶段(2)将实测的时间-沉降曲线分成相等的时间间隔Δt，本文采用30 d，从图中读出对应的时间tj及其对应的沉降值Stj；(3)以Si-1为x轴，Si为y轴，将各沉降值在(Si-1，Si)图上画出，同时做出Si-1=Si的45°直线；(4)在图中做出数据点拟合直线，并延长该直线与Si-1=Si的45°线相交，即为最终沉降量。

4.1.2 双曲线法

双曲线法是《吹填土地基处理技术规范》(GB/T 51064—2015)[17]预压地基最终沉降量及固结度推算推荐方法，其原理认为沉降量与时间的关系符合双曲线规律，因此可以通过双曲线对实测沉降曲线进行拟合，依据双曲线计算某时刻沉降量或者最终沉降量。其基本方程如下：

(4)

式中：t为满载预压时间，从满载时刻算起；S0为满载时沉降量(mm)；St为t时刻的实测沉降量(mm)。

当t趋向于∞时，得到最终沉降量：

(5)

预测步骤：(1)读取数据，选择实测沉降曲线的恒载曲线段；(2)通过双曲线拟合，确定参数a、b的值；(3)通过a、b计算t时刻的沉降量和最终沉降量。

4.1.3 三点法

基于固结度的广义解和某时刻固结度的定义，可以求出某时刻沉降量与瞬时沉降量和最终沉降量[10]的关系：

St=Sdαe-βt+S∞(1-αe-βt)

(6)

式中：Sd为瞬时沉降量，S∞为最终沉降量，α、β为与地层固结的相关参数。Sd、S∞、α、β四个未知数，通过选择实测沉降数据中的三个点(t1，S1)、(t2，S2)、(t3，S3)和(t3-t2=t2-t1)四个条件可以解出Sd、S∞、α、β四个参数的值。最终沉降量S∞为

(7)

预测步骤：(1)读取数据，对沉降数据进行光滑处理；(2)选择尽可能时间间隔大且相等的三个点，本文中三个点分别取总时间的首、尾及中间时间；(3)将选中的三个点代入上式中计算最终沉降量。

4.2 沉降预测精度分析

选取类双曲线型断面沉降数据，如图12所示，分别选取各断面恒载数据3个月、6个月和9个月，采用Asaoka法、双曲线法和三点法进行沉降预测，预测结果见图13—图15。

图12 沉降断面监测数据Fig.12 Measured settlement data

图13 3个月数据累积量各方法预测值Fig.13 Predicted value of each method under 3 months data volume

图14 6个月数据累积量各方法预测值Fig.14 Predicted value of each method under 6 months data volume

图15 9个月数据累积量各方法预测值Fig.15 Predicted value of each method under 9 months data volume

3个月数据累积量时，如图13所示，Asaoka方法的精度最差，误差超过100%。三点法和双曲线法的误差都比较小，其中双曲线的误差最小，小于40%，与最终监测沉降值较为接近，但由于数据量较少，各方法的误差均比较大。

6个月数据累积量时，如图14所示，三点法的精度最差，误差为30%左右。Asaoka法和双曲线法的误差都比较小，其中Asaoka法的误差最小，小于20%。6个月数据累积量时，各方法的准确性均显著提升。

9个月数据累积量时，如图15所示，双曲线法的精度最差，误差接近20%。Asaoka法和三点法的误差都比较小，均小于10%。9个月数据累积量时较6个月数据量，各方法的准确性均再次提升，表明各方法预测的准确性与预测数据的累积量存在正相关关系。

曲线拟合方法的预测精度与很多因素有关，特别数据量较少时，各方法预测结果的稳定性普遍较差。因此，采用曲线拟合的方法进行沉降预测，原始数据累积量必须大于3个月。Asaoka法在数据量较大时，预测精度普遍较高，建议在后续工程中广泛应用。

5 结论

本文以监测数据为基础，采用数据统计分析和曲线拟合的方法，对隧道沉降特征和各预测方法精度进行探讨，得到以下主要结论：

1)地下水位较高的砂-粉-粘互层地层明挖隧道沉降曲线可以分为类双曲线型、U型和振荡型，其中U型占比最高，达36%。

2)沉降曲线特征与回填深度比例、地下水位高度及主要压缩层土体性质存在直接关系。回填深度决定隧道上部荷载。地下水位高度与地层主要压缩层无粘性土含量(透水性)共同决定地下水浮力大小，地下水浮力是隧道抬升的主动力。

3)主要压缩层中粘性土含量与沉降量存在正相关关系，主要压缩层中粘性土含量超过64%时，沉降曲线表现为类双曲线型；粘土含量低于37%时，沉降曲线呈现振荡型的趋势。

4)恒载后数据累积时间越长，曲线拟合法预测沉降精度越高。3个月时双曲线法精度最高，误差小于40%；6个月时Asaoka法精度最高，误差小于20%；9个月时，Asaoka法和三点法预测最终沉降量误差均小于10%。建议其他工程数据累计时间较短(小于6个月)时，采用双曲线法和Asaoka法预测精度较高；数据累积时间较长(大于6个月)时，采用Asaoka法和三点法预测精度较高。