基于多模型组合的物流需求预测分析——以武汉市为例

武亚鹏，李慧颖，李 婷，刘淮源

（中南勘察设计院集团有限公司，湖北 武汉 430073）

0 引言

物流业作为国民经济发展的“血液管道”，承担着沟通产业上下游，支撑产业链发展的重要任务，在社会经济发展以及产业结构优化中起着重要作用。当前，我国正处于国民经济发展的第十四个五年规划的开端之年，各个城市已着手制定现代物流业发展“十四五”规划，其中物流需求预测是规划过程中重要的研究内容，是制定发展目标、找准发展任务的关键依据。因此，有必要针对城市物流需求预测展开研究，揭示相关机理，优化预测模型。

近些年，针对物流需求预测的研究越来越多，其基本预测方法包括：灰色预测模型、BP神经网络模型、时间序列法、向量回归等多种方法。其中，灰色预测模型、BP神经网络模型、时间序列法三种方法运用较为广泛，如郭健、杜春生、刘莉以及王晓原，等均是采用灰色预测模型，以区域、港口以及煤矿等为对象，展开物流需求预测。灰色预测模型具有样本需求量小、工作量小、精度较高等优点，但是随着迭代周期的增加，误差随之增高，因此一般适用于短期预测；文献[5-6]基于BP神经网络模型对某一城市未来的货运量及周转量进行预测，其具有自主学习的功能，但数据需求量大、计算成本高，同时难以解释自变量与因变量之间的函数关系以及影响机理；李明书，等采用时间序列法中的ARIMA模型对长春市2017-2020年共37个月的邮政物流总量数据进行研究，构建物流需求预测模型。时间序列法是以历史数据变化趋势为预测基础，无法对市场变化、经济增速变化等相关因素的影响作出反应。

综上所述，单一预测方法均存在无法避免的技术缺陷，导致预测结果准确性降低。耿立艳，等认为组合模型能够有效提高单一预测方法的精度。王燕，等对指数增长模型和灰色预测模型各自计算权重，线性相加后得到组合模型，对广州市物流需求进行了预测，其预测结果相对误差控制在3%以内。薛禀凡利用熵值法确定多元回归模型、灰色预测模型及趋势预测模型的权重比例，构建组合模型，模型预测精度得到有效提升。

因此，本文针对灰色预测模型、线性回归模型及时间序列法等三种预测模型，合理确定各自权重，组合成新的预测模型，对湖北省武汉市未来10 年（即2021-2030年）的物流需求进行预测，为城市现代综合交通物流规划提供参考。

1 单一模型预测分析

1.1 指标选取及基础数据分析

本文选取货运量作为物流需求预测指标，并统计了武汉市2000-2019 年的地区生产总值和货运量作为基础数据，其中货运量为公铁水空等运输方式的总量，具体见表1。

1.2 GM(1,1)灰色预测模型分析

GM(1,1)灰色预测针对一个变量，通过少量的信息，建立灰色一阶微分预测模型，对事物发展规律作出长期描述，其本质上是通过累加的方式，以减弱数据所呈现的随机性，从而预测事物未来发展趋势，本文选取武汉市2010-2019年货运总量作为预测变量，具体预测过程如下：

（1）计算数列的级比。

其中，y表示原始数据列[y(1),y(2),...,y(n)]，n表示数据个数，取值为10；λ（k）表示数列级比，将原始数据代入得到max[λ（k）]为1.01，min[λ（k）]为0.85，即e＜λ（k）＜e，y数列能够满足GM(1,1)模型条件。

（2）数据累加。

表1 武汉市2000-2019年地区生产总值及货运量统计表

其中，y表示原始数列1次累加后所生成的新数列。

（3）计算新数列y(k)紧邻均值。

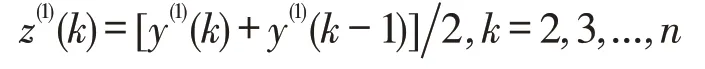
其中，z(k)表示新数列y(k)的紧邻均值数列。

（4）建立GM（1,1）模型。

其中，a 表示发展系数；b 表示灰色作用量；将数据列带入方程，采用最小二乘法求得a，b 值分别为-0.062 1，5 948.811 5；经计算模型后验差c 值为0.052 6，小于0.35，表示模型精度等级良好。

于是得到预测公式为:

即：

1.3 线性回归预测分析

本文采用一元线性方程进行分析，并选取2000-2019年武汉市地区生产总值作为自变量，货运量作为因变量。经计算得出，模型拟合度R为0.95，表示二者拟合度良好，方程常数项g为11 809.464，自变量回归系数M为3.587，即预测方程为：

其中，y表示因变量货运量；g表示方程常数项；M表示自变量回归系数；x表示自变量地区生产总值。依据《武汉市国民经济和社会发展第十四个五年规划和2035 年远景目标纲要》对武汉市经济增速进行预测，从而得到自变量x预测值，带入公式对武汉市货运量进行预测。

1.4 时间序列法预测分析

时间序列法预测模型在物流需求预测、交通量预测等方面应用广泛，其中ARIMA模型较为常用，因此本文采用ARIMA模型对武汉市货运需求进行预测。

ARIMA（p,d,q）模型的结构如下：

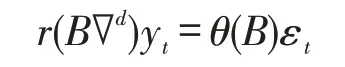
其中，y表示t时间节点城市物流需求（货运量）数值；∇=(1-B)，d表示差分次数，B表示延迟算子且By=y；r(B)=1-rB-…-rB表示自回归系数多项式，p表示自回归阶数，r，r，...，r表示自回归参数；θ(B)=1-θB-θB-…-θB表示移动平滑系数多项式，q表示移动平均阶数，θ,θ,…,θ表示移动平滑系数；ε表示残差或白噪声序列。

本文以武汉市2000-2019 年货运量作为基础数据，利用SPSS 软件进行计算，计算结果显示：ARIMA（0,2,2）模型平稳R为0.979，表示模型拟合度良好，并向后预测11期。

2 单一模型预测结果分析

通过对三种模型方法的计算分析，即可得到武汉市2021-2030年货运量预测值，如表2及图1所示。

表2 武汉市2021-2030年物流需求（货运量）单一模型预测结果（单位：万t）

总体来看，线性回归模型与灰色预测模型结果相近，至2030年武汉市货运总量在128 000万t左右；时间序列预测模型结果则处于较大的数据范围，至2030年武汉市货运总量达到167 000万t以上，与另外两个模型结果差距在39 000万t以上。单一模型之间的预测机理、预测结论并非完全一致，采用简单的求平均数法难以综合考虑各种预测因素求得合理的预测结果。因此，有必要针对单一模型的组合方法进行研究，以便科学预测武汉市未来10年物流需求（货运量）发展趋势。

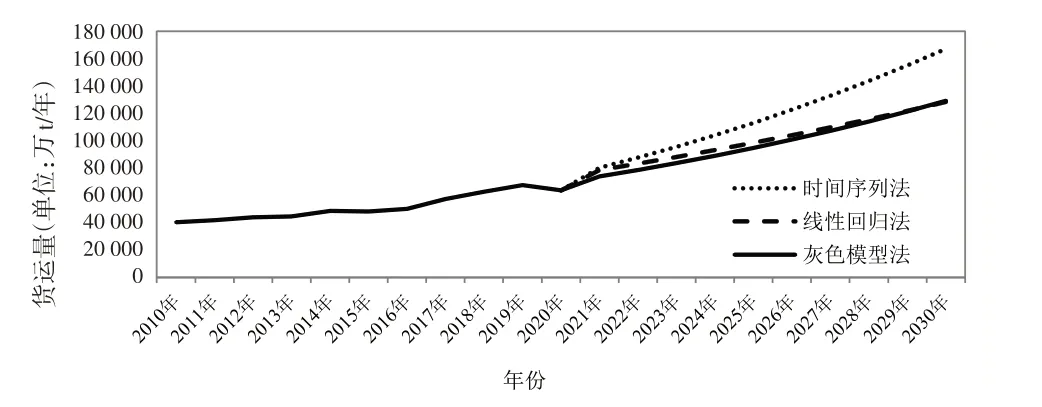
图1 单一模型预测结果

3 模型组合分析

3.1 模型组合方法选取

模型组合的基本思想即是将不同模型的预测结果按照一定比例关系，采用线性或非线性的方法进行加权计算，从而得到一个或一组综合所有结果的、全新的预测数据，其关键环节是各模型权重比例的科学确定，常用的方法包括：优势矩阵法、方差倒数法、标准差法、有效度法等。本文选用有效度法对单一模型的权重系数进行计算，具体计算公式如下：

其中，S表示模型有效度；v表示模型第t期实际值；v̂表示模型第t期预测值；n 表示预测期数，本文取值为10。

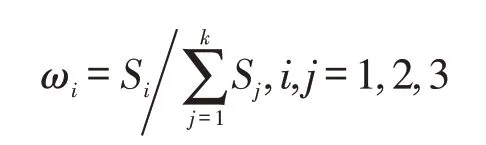
其中，ω表示第i个模型的权重比例；S表示第i个模型的有效度。

3.2 单一模型全权重计算

根据上述计算过程可知，各模型有效度的计算是权重比例确定的关键，但由于无法获取武汉市未来年份货运量的实际值，采用未来年份作为研究对象，难以正确计算模型有效度。因此，可将武汉市2010-2019年货运量作为研究对象，运用各单一模型对其进行反向预测，得到货运量的预测值和实际值，从而获取模型有效度计算基础数据，具体计算结果见表3。

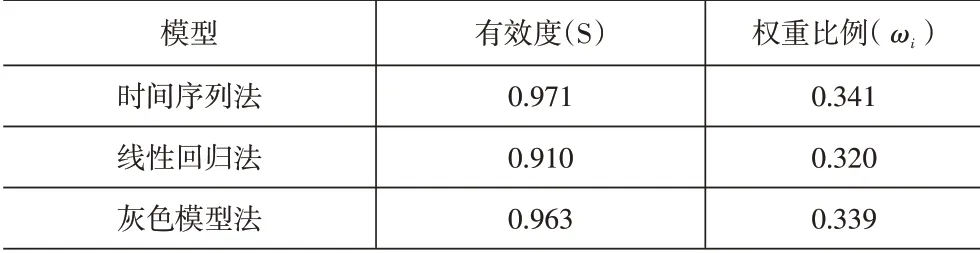
表3 单一模型有效度及权重比例计算结果

3.3 模型组合计算分析

根据上述权重计算结果，采用线性相加的方法即可得到基于多模型组合的物流需求预测公式，具体如下：

其中，y(n)表示第n 期组合模型货运量预测结果，n 取值为1，2，…，10；y(n)表示n 期时间序列法ARIMA（0,2,2）模型货运量预测结果；y(n)表示n期线性回归模型货运量预测结果；ŷ(n)表示n期灰色模型货运量预测结果。

以2010-2019年货运量作为研究对象，将其预测值带入组合模型及单一模型公式，得到模型预测结果，并与实际值进行对比，得到组合模型最大误差率为5.56%，平均误差率为2.94%；灰色模型最大误差率为9.27%，平均误差率为4.35%；线性回归模型最大误差率为9.74%，平均误差率为5.27%；时间序列法最大误差率为8.10%，平均误差率为4.26%。纵向对比可知，组合模型预测精度得到有效提高，误差整体上处于可接受范围，即该模型可以有效对武汉市物流需求（货运量）进行预测，具体如图2所示。

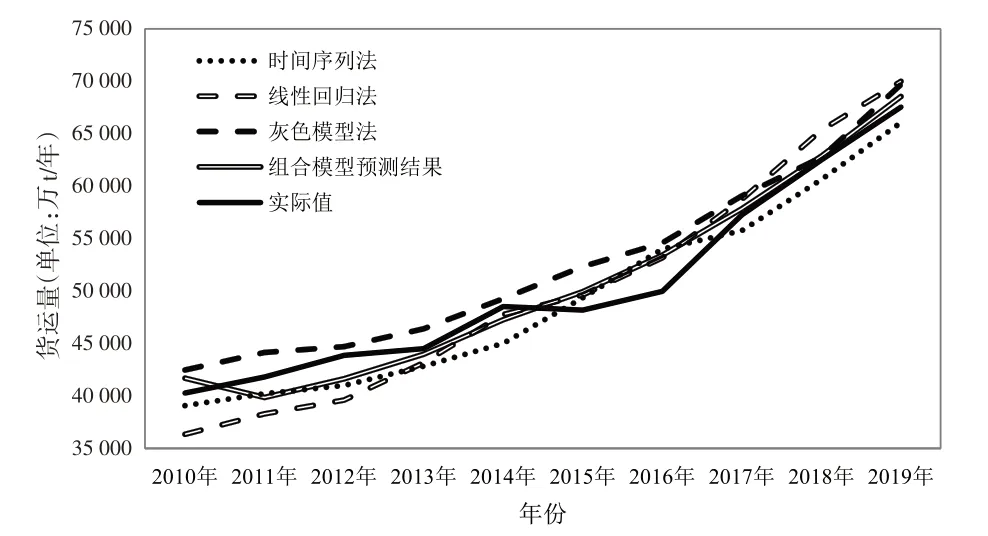
图2 2010-2019年武汉市货运量单一模型、组合模型预测值与实际值对比

因此，将2021-2030年单一模型预测结果带入组合模型公式，即可得到武汉市未来10年物流需求（货运量）的最终预测结果，见表4。

预测结果显示，武汉市未来十年物流需求（货运量）处于持续增长的状态，但随着经济增速的减缓，增长率有所放缓，至2030 年武汉市年货运量将达到141 819万t，年增长率为6.61%，略高于经济增速预测值。

4 结语

通过误差分析可知，组合模型在预测精度方面，相较于单一模型有所提升，平均误差率降低至2.94%，处于合理的误差范围。组合模型预测结果显示，至2025 年武汉市物流需求水平将越过10 亿t 大关，至2030年将达到上海市现有需求水平，其物流业发展前景广阔。面对未来巨大的物流需求规模，武汉市应积极着手制定物流业中长期发展规划，强化物流基础设施规划建设，着力构建现代物流体系，推进物流业降本增效，推动物流业高质量发展。同时，本文模型在预测过程中针对政策影响等相关因素的考虑存在不足，在后续的研究中将采用定量与定性分析的方法进一步优化模型。

表4 武汉市2021-2030年物流需求（货运量）预测结果 单位：万t