长江流域可能最大降水的时空变化特征
刘延志 李佳佳
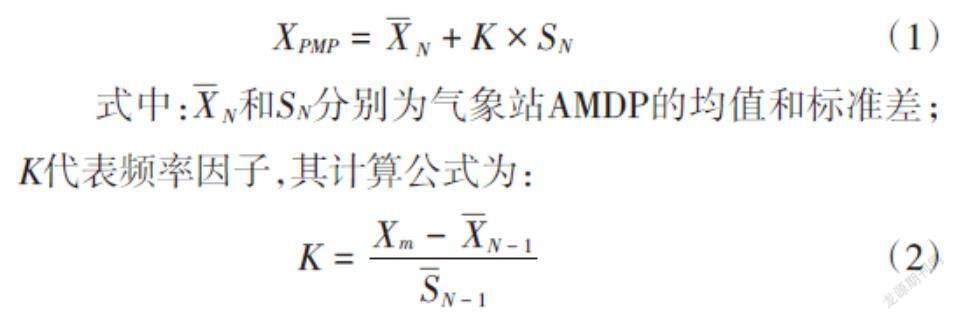




摘 要:基于长江流域188个气象站1963—2018年的日降水观测数据,采用改进的Mann-Kendall(MMK)方法检验流域内各站点年最大日降水量(AMDP)的变化趋势,利用改进的Hershfield法估算所有站点的可能最大降水(PMP)并分析其时空变化特征,以揭示气候变化对PMP产生的影响。结果表明:1963—1992年和1989—2018年流域内大多数站点的AMDP呈非显著变化趋势,用于估算这2个时期的PMP具有一定的合理性;2个时期的AMDP均值及其标准差均呈现西北低东南高的空间格局,且与1963—1992年相比,流域内1989—2018年大多数站点的AMDP均值及其标准差呈增加趋势;2个时期的PMP均呈东高西低的空间分布特征,且1989—2018年流域的PMP较1963—1992年平均增加约28.28%,其中79.79%站点的PMP呈增加趋势,增加趋势显著的站点主要分布在川西高原、南阳盆地和长江以南地区。
关键词:可能最大降水;改进的Hershfield方法;频率因子;长江流域;时空变化特征
中图分类号 P426.6 文献标识码 A 文章编号 1007-7731(2022)10-0150-06
Spatiotemporal Variation Characteristics of Probable Maximum Precipitation in the Yangtze River Basin
LIU Yanzhi LI Jiajia
(College of Geographic Sciences, Hunan Normal University, Changsha 410081, China)
Abstract: Based on the observed daily precipitation during 1963—2018 at 188 meteorological stations in the Yangtze River Basin, the Modified Mann-Kendall (MMK) method is used to analyze the trends of the temporal variations in Annual Maximum Daily Precipitation (AMDP). Then Probable Maximum Precipitation (PMP) is estimated by the modified Hershfield statistical method and the spatiotemporal variation characteristics of PMP are analyzed for all stations over the basin, as a result, to reveal the possible impact of climate change on PMP. The results show that AMDP shows nonsignificant increasing or decreasing trend at most stations of the basin during 1963—1992 and 1989—2018 period so that it is reasonable to use them for PMP estimation. The mean and standard deviation of AMDP shows a spatial pattern of higher values in southeast and lower values in northwest, and an increasing trend at most stations during 1989—2018 relative to 1963—1992. The PMP during two periods is characterized by the spatial distribution with higher values in east and lower values in west. Compared to 1963—1992, the average PMP over the basin increases by 28.28% during 1989—2018, and there are 79.79% stations, mostly located in the western Sichuan Plateau, Nanyang Basin and the south region over the Yangtze River Basin, showing that PMP increases significantly.
Key words: Probable maximum precipitation; modified Hershfield method; frequency factor; Yangtze River Basin; spatiotemporal variation characteristic
氣候变化会改变全球水文循环过程,从而改变降水的时空变化规律[1-2]。IPCC(Intergovernmental Panel on Climate Change)第六次报告[3]指出,21世纪内全球气温上升将超过1.5~2℃,世界各地特别是亚洲地区极端降水事件风险将进一步加剧。在全球变暖的背景下,极端降水事件不断增加已成为不可争论的事实[4]。而极端降水是造成洪涝灾害频发的重要原因之一,往往会给社会经济和生态发展等方面带来巨大的危害,引发了社会各界的广泛关注[5]。可能最大降水[6](PMP)是在现代气候条件下,某一设定流域在一定历时内的最大降水深度,代表一种相对极端降水事件,已有许多研究学者利用PMP来估计极端降水[7-8]。虽然PMP不考虑长期的气候变化趋势,但随着气候变暖,极端强降水事件不断增加,导致气候变化对PMP可能产生的影响不容忽视。已有大量研究[9-12]表明,在气候变化的不断影响下,全球大部分地区的PMP可能出现了不同程度地增加。如Kunkel等[10]使用全球气候模式(GCMs)模拟的降水数据,探究了气候变化对PMP的影响,结果表明,未来全球范围内的PMP呈增加趋势,特别是到2071—2100年美国大陆的PMP将会增加20%~30%。Afrooz等[12]以1971—2000年为基准期,预估了伊朗南部地区的PMP,结果显示PMP的增加幅度为18.2%~27.3%。
长江流域面积广阔,地貌类型和气候条件复杂多样,降水的时空分布很不均匀且年际变化大[13]。作为中国气候变化响应的敏感区域,近年来长江流域极端降水趋于增多,洪涝灾害频发,致使大坝和水电站的建设以及城市化进程受到了严重影响。然而,关于气候变化对长江流域PMP时空变化的影响研究仍较少。因此,在当前气候条件下估算长江流域的PMP,研究PMP的时空变化特征及其对气候变化的响应很有必要,这不仅有助于水文工程的风险评估,而且对气候变暖背景下极端降水事件的预估也具有重要意义。
目前,估算PMP的方法主要包括统计估算法和水文气象法两大类[14]。其中,由Hershfield[15]开发的统计估算法是世界气象组织(WMO)推荐的估算PMP的主要方法之一,其计算简便,在资料允许的条件下,Hershfield法可以快速估算PMP以提供实际参考。兰平等[7]利用Hershfield法和暴雨移置法估算了香港地区的PMP。吴成兴等[8]分别采用Hershfield法和水文气象法计算金沙江流域不同历时的PMP,结果表明,利用Hershfield法计算PMP是有效可行的。值得注意的是,采用Hershfield法估算PMP时,频率因子(K)起着关键的作用,然而在较少发生极端降水的地区,传统的上包络线方法会导致PMP的估算结果过高。本研究采用Sarkar等[16]提出的改进上包络线方法来确定新的频率因子,以此来估算长江流域各气象站的PMP。
因此,本研究基于长江流域188个气象站的日降水观测数据,采用改进的Hershfield法估算该流域的PMP,并分析了流域PMP的时间变化和空间分布特征,揭示气候变化对PMP可能产生的影响,以期为流域内资料缺乏地区PMP的计算和流域可能最大洪水计算提供参考。
1 数据与方法
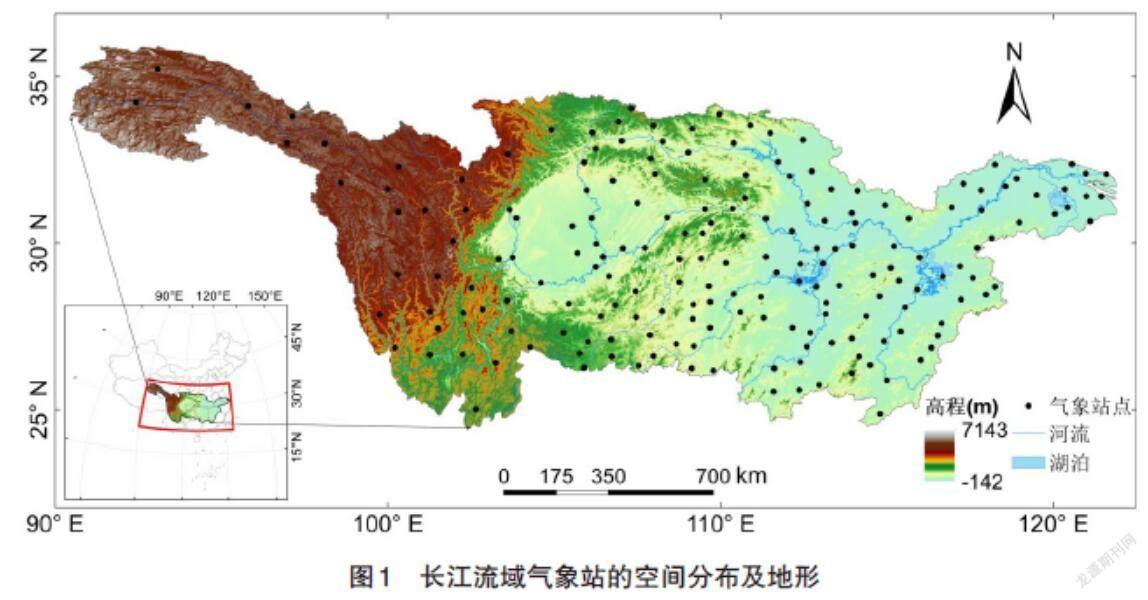
1.1 数据资料 本文所使用的气象数据为长江流域188个气象站(图1)1963—2018年实测日降水数据,下载于中国气象科学数据共享服务网(http://www.escience.gov.cn/metdata/page/index.html)。根據WMO指南,获取极端气候变量的特征时,应采用不少于30年的时间序列作为气候预测的标准期。因此,本文将长江流域1963—2018年的观测数据分为2个30年的窗口时期(1963—1992年和1989—2018年)进行PMP的计算和分析。
1.2 研究方法
1.2.1 Modified Mann-Kendall检验 Mann-Kendall(MK)检验法是一种非参数统计检验方法,常用于水文、气象等时间序列的趋势检验[17]。由于降水序列可能存在自相关性,会影响趋势检验结果的可靠性[18]。为了消除该影响,本研究采用Modified Mann-Kendall(MMK)检验[19]方法分别对长江流域188个气象站点的年最大日降水量(AMDP)进行趋势分析,并进行显著性检验,显著性水平设为5%,具体算法参见文献[19]。
1.2.2 改进的Hershfield法 统计估算法是Hershfield于1961年提出的,该方法主要是根据实测降水量求出统计量K以估算PMP。计算公式如下:
[XPMP=XN+K×SN] (1)
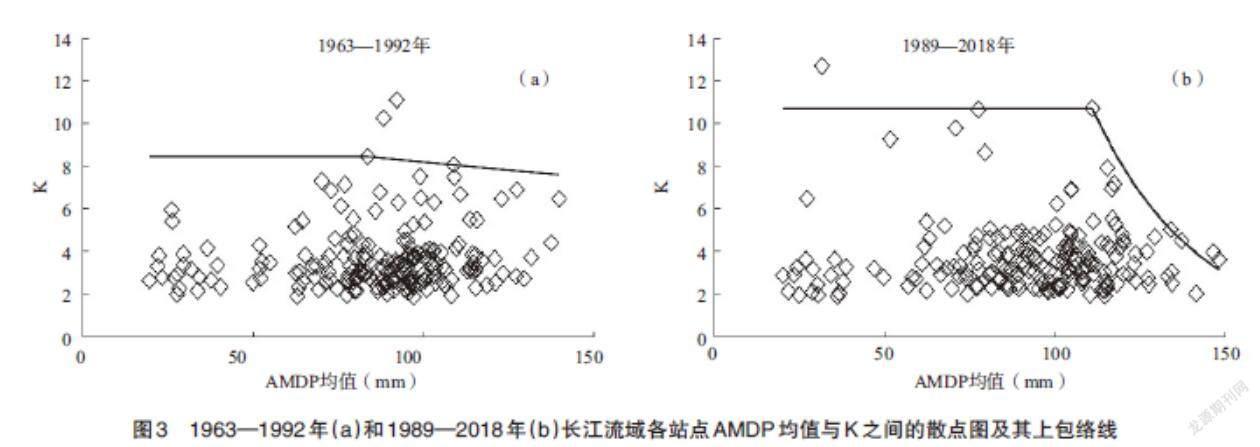
式中:[XN]和[SN]分别为气象站AMDP的均值和标准差;[K]代表频率因子,其计算公式为:
[K=Xm-XN-1SN-1] (2)
式中:[Xm]为AMDP的最大值;[XN-1]和[SN-1]分别为AMDP剔除最大值后的均值和标准差。
由于K过大会导致PMP的估算结果过高,使水利设施的设计成本增大,而K过小会导致PMP过低,水利设施则面临更高的风险。因此,为了使PMP的估算结果更合理,Hershfield[20]对公式(2)的K拟合上包络线以确定新的频率因子。计算公式如下:
[K=KAe-bXN] (3)
式中:[KA]为AMDP均值最小的点的[K]值;[b]为指数衰减的斜率。然而,在较少发生极端降水地区这种传统的包络线方法会导致的PMP估算结果过高。因此,本文采用改进的上包络线方法线来确定K,公式[16]如下:
[K=Km , 0<XN<XtNKm e-b(XN-XTN), XN>XtN] (4)
式中:[Km]为该流域所有气象站K的最大值;[XtN]表示[Km]点处AMDP的均值。具体算法参见文献[21][21]。
2 结果与分析
2.1 AMDP变化趋势 利用AMDP估算PMP时,需确保AMDP时间序列没有显著的上升或下降趋势[22]。故本研究在0.05的显著性水平下,分别对流域内188个气象站1963—1992年和1989—2018年的AMDP进行MMK趋势检验分析。图2展示了所有气象站在2个时期内AMDP的时间变化趋势检验结果。从图2可以看出,2个时期内大多数站点的AMDP呈非显著变化趋势,仅少数站点的AMDP呈显著的上升或下降趋势,散布于流域内。因此,在气候变化条件下,利用流域188个气象站实测的AMDP估算各站点的PMP是合理的。
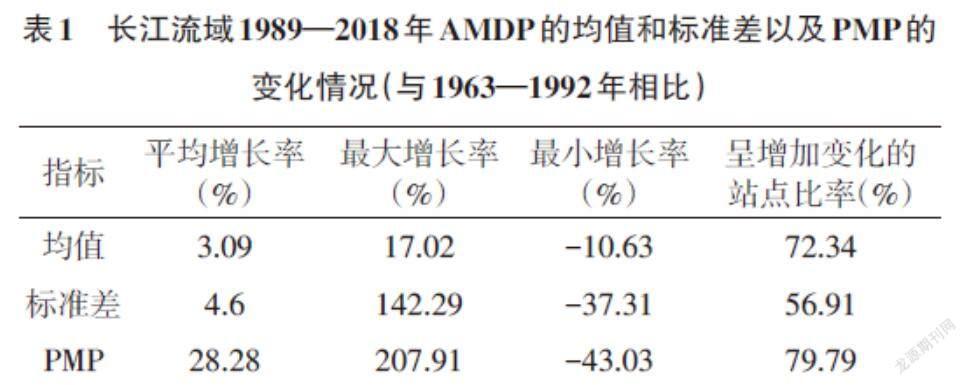
2.2 构建区域包络线 绘制1963—1992年和1989—2018年188个站点的K与其AMDP均值之间的散点图以构建改进的上包络线,结果如图3所示。从图3可以看出,改进后的包络线由一条平行于横轴的直线和一条指数衰减的曲线组成,且在1989—2018年K的指数衰减速度更快。这一观察结果与Lee等[17]和Desa[23]等的发现是一致的。此外,从图3还可以观察到,多数站点的K值集中在2~6。而在图3a和3b中分别存在2个和一个明显的异常点,正如Sarka等[16]所指出的,若将异常点作为[Km]会导致研究区域的PMP估算结果过高。因此,剔除异常点后,通过构建上包络线确定新的频率因子,而在异常点处则使用其原始的频率因子,然后估算流域内各个气象站的PMP。
2.3 PMP的时空变化特征 为分析长江流域1963—1992年和1989—2018年PMP的时空变化特征,基于AMDP的均值和标准差以及改进的频率因子K,利用改进的Hershfield法分别计算了流域188个气象站在这2个时期的PMP值。然后,利用克里金插值方法绘制了流域AMDP均值及其标准差、K和PMP的空间分布图(见图4)。观察图4a和4b可以发现,在2个时期内AMDP均值具有相似的空间分布特征,均表现出明显的空间差异性,即AMDP均值大致呈现出西北低东南高的空间格局。具体地,青藏高原的AMDP均值最小,长江中下游平原的AMDP均值最大,同时,在流域中部的四川盆地地区存在一个高值中心。这与该流域降水自东南向西北逐渐减少,且四川盆地为降水高值区的降水特征相吻合[24]。从图4c和4d中可以观测到,在流域中西部地区存在1条沿东北-西南方向的分界线,界限以东地区的AMDP标准差明显高于界限以西地区,同时,在界限以东的四川盆地西南部、洞庭湖流域西北部和鄱阳湖北部地区均存在高值中心。一个地区的AMDP标准差越大,则表明该地区AMDP的波动幅度越大,极端降水年际变化幅度就越大。图4e和4f给出了该流域2个时期内K的空间分布图,可以看出绝大部分地区1963—1992年的K值在8~8.5,而1989—2018年的K值除鄱阳湖流域东北部地区以外均大于9。这表明长江流域1989—2018年的K值相对于1963—1992年明显升高,这势必会造成流域1989—2018年的PMP值有所升高。图4g和4h分别展示了长江流域在1963—1992年和1989—2018年PMP的空间分布情况,可以观察到,2个时期的PMP均呈现东高西低的空间分布特征,特别地,四川盆地和长江中下游地区1989—2018年的PMP较前一时期明显增加。之前有研究指出,长江流域降水的极值中心处于湖北省东南部、江西省东北部和安徽省南部交界处,主要原因是由于受到地势海拔和东亚夏季风的影响,有利于长江流域梅雨锋的长期停留,进而导致长江中下游极端降水增加的可能性变大[25]。而四川盆地西部地區位于青藏高原东部位置,当偏东气流盛行时,盆地西部的山区地形产生抬升作用,导致该地区更易发生强降水事件[26],因此四川盆地地区的PMP较高。
为了直观地反映AMDP和PMP的变化情况,分别计算流域188个站点1989—2018年的AMDP均值和标准差以及PMP相较于1963—1992年的增长率,其空间分布如图5所示。同时,表1列出了流域所有站点的AMDP均值和标准差以及PMP的平均变化情况。观察图5c和表1可知,流域内有79.79%站点的PMP呈增加趋势,其中,增加趋势显著的站点主要分布在川西高原、南阳盆地和长江以南地区,PMP的变化范围在-43.03%~209.91%。然而,在整个长江流域,PMP的平均增长率为28.28%。这表明1989—2018年流域整体的PMP明显增加。PMP的变化与AMDP的平均值和标准差密切相关。从图5a、5b和表1可以看出:1963—2018年流域内AMDP的均值和标准差呈现出不同的变化趋势,有72.34%站点的AMDP均值呈增加趋势,且增加趋势最明显的地区位于流域的东北部和洞庭湖流域的西南部。与AMDP的均值相比,其标准差显示出更高的变化范围,最大增长率为142.29%,说明1963—2018年流域内极端降水的年际变化幅度更大。流域内有56.91%的站点AMDP的标准差呈增加趋势,增加趋势最明显的地区位于流域西部的川西高原。在气候变化的影响下,长江流域大部分地区的AMDP均值和标准差逐渐增加,这意味着区域内极端降水的变异性明显增强,导致PMP增加。
3 结论
本研究结果表明:
(1)流域1963—1992年和1989—2018年大多数站点的AMDP呈非显著变化趋势,因而用于估算2个时期的PMP具有一定的合理性。
(2)AMDP均值在1963—1992年和1989—2018年这2段时期内大致呈现出西北低东南高的空间格局,且与1963—1992年相比,1989—2018年流域内有72.34%的站点的AMDP均值呈增加趋势,且增加趋势最明显的地区位于流域的东北部和洞庭湖流域的西南部。与AMDP均值相比,AMDP标准差显示出更高的变化范围,增加趋势最明显的地区位于流域西部的川西高原。
(3)PMP的变化与AMDP的平均值、标准差密切相关。流域1963—1992年和1989—2018年的PMP均呈现东高西低的空间分布特征。与前一时期相比,流域1989—2018年的PMP平均增加28.28%且有79.79%站点呈增加趋势。其中,增加趋势较明显的站点主要分布在川西高原、南阳盆地和长江以南地区。
参考文献
[1]李峰平,章光新,董李勤.气候变化对水循环与水资源的影响研究综述[J].地理科学,2013,33(04):457-464.
[2]姜彤,孙赫敏,李修仓,等.气候变化对水文循环的影响[J].气象,2020,46(03):289-300.
[3]IPCC,Climate Change 2021:The Physical Science Basis.Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change[R]. New York:Cambridge University Press,2021.
[4]Berg P,Moseley C,Haerter J O.Strong increase in convective precipitation in response to higher temperatures[J].Nature Geoscience,2013,6(3):181-185.
[5]高涛,谢立安.近50年来中国极端降水趋势与物理成因研究综述[J].地球科学进展,2014,29(05):577-589.
[6]World Meteorological Organization(WMO). Manual for estimation of probable maximum precipitation[M].Geveva:WMO,2009,No.1045.WMO,2017.WMO guidelines on the calculation of climate normals.World Meteorol.Organ.29.
[7]兰平,林炳章,陈晓旸,等.基于改进的统计估算法与暴雨移置法的香港地区4h可能最大降水估算[J].水电能源科学,2018,36(09):5.
[8]吴成兴,李国芳,杨百银,等.基于卫星降水数据的金沙江流域可能最大降水量计算方法[J].水电能源科学,2020,38(02):5-8.
[9]Katelyn A.Johnson,Jeffrey C.Smithers.Updating the estimation of 1-day probable maximum precipitation in South Africa[J].Journal of Hydrology:Regional Studies,2020,32:100736.
[10]Kenneth E.Kunkel,Thomas R.Karl,David R.Easterling,et al.Probable maximum precipitation and climate change[J].Geophysical Research Letters,2013,40(7):1402-1408
[11]Lee O,Park Y.,Kim E S,et al.Projection of Korean probable maximum precipitation under future climate change scenarios[J].Advances in Meteorology,2016,13:1-16.
[12]Afrooz A.H.,Akbari H,Rakhshandehroo G R,et al.Climate change impact on probable maximum precipitation in Chenar-Rahdar River Basin[J].Watershed Management,2015(08):36-47.
[13]孙惠惠,章新平,黎祖贤,等.长江流域不同类型降水量的非均匀性分布特征[J].长江流域资源与环境,2019,28(06):1422-1433.
[14]林炳章,兰平,张叶晖,等.可能最大降水估算研究综述[J].水利学报,2018,049(001):92-102,114.
[15]Hershfield D M.Method for Estimating Probable Maximum Rainfall[J].American Water Works Association,1965,57(8):965-972.
[16]Subharthi Sarkar,Rajib Maity.Increase in probable maximum precipitation in a changing climate over India[J].Journal of Hydrology,2020,585:124806.
[17]HAMED K H.Trend detection in hydrologic data:The Mann–Kendall trend test under the scaling hypothesis [J].Journal of Hydrology,2008,349(3-4):350-363.
[18]章诞武,丛振涛,倪广恒.基于中国气象资料的趋势检验方法对比分析[J].水科学进展,2013,24(04):490-496.
[19]Khaled H.Hamed,A.Ramachandra Rao.A modified Mann-Kendall trend test for autocorrelated data[J]. Journal of Hydrology,1998,204(1):182-196.
[20]Hershfield D M.Estimating the Probable Maximum Precipitation [J].American Society of Civil Engineers,1961,87(5):99-106.
[21]Chavan S R,Srinivas V V.Regionalization based envelope curves for PMP estimation by Hershfield method [J].International Journal of Climatology,2017,37(10):3767-3779.
[22]Beauchamp J,Leconte R,Trudel M,et al.Estimation of the summer-fall PMP and PMF of a northern watershed under a changed climate[J].Water Resources Research,2013,49(6):3852-3862.
[23]Desa M M N,Rakhecha P R.Probable maximum precipitation for 24-h duration over an equatorial region:Part 2-Johor,Malaysia [J].Atmospheric Research,2007,84(1):84-90.
[24]卢萍,杨康权.四川盆地三个典型落区西南涡暴雨天气成因的对比分析[J].高原山地气象研究,2017,37(3):16-20.
[25]Zhang Q,Xu C Y,Zhang Z,et al.Spatial and temporal variability of precipitation maxima during 1960-2005 in the Yangtze River basin and possible association with large-scale circulation[J].Journal of Hydrology,2008,353(3-4):215-227.
[26]胡思,曾祎,王磊,等.长江流域极端降水的区域频率及时空特征[J].长江流域资源与环境,2019,28(08):2008-2018.
(責编:张宏民)

