基于改进K-means算法的学生用户画像构建研究

许智宏，李彤彤，董永峰，董 瑶

（1.河北工业大学 人工智能与数据科学学院，天津 300401；2.河北工业大学 河北省大数据计算重点实验室，天津 300401）

0 引言

校园一卡通中各种信息、资源的集成和优化，能够实现信息的有效配置和充分利用，同时一卡通作为数字校园建设重要组成部分，对学生个体发展和高校发展有着至关重要的作用。目前国内很多科研工作者对一卡通进行了相关的研究工作。姜楠和许维胜[1]以校园一卡通日常消费数据为研究对象，对学生消费习惯进行分析，运用改进初始中心点的K-means 算法通过类内密度程度高低来判定优化初始中心点的选择，对学生消费习惯进行聚类，采用Apriori算法对学习行为进行关联度分析，协助高校学生工作人员分门别类对学生进行管理；黄刚等[2]采用K-means算法以校园一卡通数据为研究对象，通过做方差图的方式对k值进行取值，分析学生的消费习惯后对学生特征进行画像，该方法选择多特征对学生画像做出了基础详细分析，但是并未在算法层面上进行改进；韩伟等[3]用K-means算法将大学生餐饮消费行为按群体分类，侧重分析时间、地点和交易金额，关联成绩预测不同层次学习成绩的学生的餐饮习惯，研究侧重应用，同样未对算法过多叙述。

事实上，一个好的算法对于数据分析尤为重要，熊忠阳等[4]提出了一种基于密度的思想优化初始聚类中心选择的方法——最大距离法，在收敛速度和准确率上有大大提高，但是手动输入密度系数，算法可伸缩性受限；刘静[5]以数据中心点之间距离和数据内部以及数据间的差异度比值作为评估函数来确定初始中心点，提高了聚类算法的效率，但是数据量的大小同样会影响效率；Shadab Irfan等[6]使用遗传算法迭代的方式最小化目标函数和相似度函数，降低了函数的时间复杂度。

以上研究对于算法的改进均达到一定效果，但是数据特征的分散度相对较弱，数据特征的个性影响表示并不突出，未达到加强数据集特定功能的效果。因此，本研究采用DPCA-K-means算法建立数据分析模型，对多维数据特征进行降维处理，分散数据点后对新的权重特征求得数据均值作为初始质心，多次分配数据点进行聚类分析，通过增加每个特征的数据分析的个性影响，对不同行为特征的用户对比成绩进行类别划分，研究影响学生行为与成绩之间的关系。

1 用户画像模型构建

用户画像是通过收集用户行为数据、统计属性、分析特征，全面细致地挖掘用户的特征并抽象出标签化的用户模型。用户画像侧重于对用户进行不同维度的划分。在学生用户画像的构建过程中，利用高校一卡通数据对现有学生行为进行分析判定，其中消费数据属性主要涵盖交易额、交易时间、交易类型等多维，这些特征中多个数据特征或其特征组合对最终学生分类的影响较小甚至没有影响。因此，多维度数据需要重新进行组合研究，提升数据表达的客观全面性。

本文采用改进基础模型K-means聚类算法和主成分分析（Principal Component Analysis，PCA）算法[7]对学生行为进行用户画像[8]，将学生用户按照其行为习惯归类，区别不同学习成绩中众多学生行为习惯的共性特征，辨识不同行为特征用户的差异特征，帮助掌握用户行为和成绩的规律。改进的PCA算法即DPCA算法主要是用来改善数据特征对于数据分析实验影响因素的情况，在本研究中用来对高维度特征进行重要度分析并赋予特征值权重，而K-means算法主要是实现对数据的基础聚类[9]，本研究主要创新是在特征多样性的基础上分析特征的重要度并进行数据点新权重规划，在保留尽可能大特征的基础上增加特征之间的差异性，对K-means算法进行中心点选择的改进[10]结合多次算法实验，避免K-means陷入局部最优，提高算法准确率。

1.1 K-means 算法基本思想

K-means算法是一种通过均值聚类数据点的无监督的学习算法[11]，算法的关键是保证在各个中心点之间相互远离的情况下随机选择不同位置的聚类中心[12]。核心思想为：选定聚类簇的个数k，随机选择样本作为初始质心，依次考察每个样本与当前质心的距离[13]，选定距离最近的簇后归类。所有样本考察结束一轮后，分别更新每个簇的质心，不断重复上述过程，直到质心不再发生变化，算法结束。k个聚类簇具有以下特点：各个聚类内数据点尽可能紧凑，各聚类簇之间数据点尽可能远离[14]。算法的最终收敛条件采用最小化误差平方和目标函数[15]。聚类过程及其结果总体受到基础中心点选择的影响，均值聚类算法性能的关键就在于聚类中心的合理选取。其中误差平方和的定义如式（1）：

式中：X为数据集中的数据点；Ci为质心。

TSS是严格的坐标下降（Coordinate Decent）过程，采用欧式距离作为变量之间的测度函数。每次趋近一个变量Ci的方向找到最优解；目标函数TSS求偏导数，令其等于0后，得式（2）；

式中：k表示Ci所在的簇的元素的个数。

当前聚类的均值是当前方向的最优解（最小值），与K-means的每次迭代过程一样，保证TSS每次迭代后数值变小，最终收敛。但由于TSS是一个非凸函数（non-convex function），所以TSS并不能保证找到全局最优解，只能确保局部最优解。为防止K-means 算法局部最优在处理数据的过程中采用DPCA 方式，即对数据进行降维处理后将数据重新进行再次投影，保留全部特征信息，记下每个特征的权重，且多次执行Kmeans算法，最终选取最小的TSS为最终结果。

1.2 主成分分析算法基本思想

主成分分析算法（Principal Component Analysis）是利用降维的思想[16]，将多个变量转化为少数几个综合变量（即主成分），每个主成分都是原始变量的线性组合，各主成分之间互不相关[17]，且能够反映始变量的绝大部分信息。算法目标是计算出一组投影向量，将原始数据投影到一个维数较低的子空间，然后对这个子空间中的特征相似程度进行比较，从而实现对测试样本的划分，可以克服数据高维度造成的算法执行效率降低的问题，将复杂因素归结为几个主成分，使得复杂特征得以简化[18]。在算法执行过程中遵循最大可分性和最近重构性原则，即数据点投影点尽可能分开，样本点到投影平面的距离足够近。PCA通过寻找一组线性投影向量，使得投影后得到的低维数据能够尽可能多地保持原始数据的主要信息。理论研究表明，如果随机变量的方差越大，则这些变量中所携带的信息就越多，若某一个特征的方差为零，那么该特征则为常量，对数据分析无任何影响。

PCA算法无法考虑不同样本在识别过程中存在的重要度差异。它虽然能够将原始数据通过线性变换矩阵从高维空间映射到低维空间，但它是平均地对待每一维特征，以各个维度特征欧氏距离上的重建误差和最小为目标，无法实现特征的个性化提取。然而各样本特征之间对于实验结果的影响势必一样的，这就需要考虑用特征的权重系数来刻画数据，因此采用特征权重系数的DPCA算法进行特征分析。算法流程如下：

步骤1 对数据集X中的每一个特征属性进行标准化处理；

步骤2 求出数据中心化后矩阵X特征与特征之间的协方差，构成的协方差矩阵R[19]；

步骤3 对协方差矩阵做特征值分解，求特征值和特征向量；

步骤4 将特征向量按照特征值贡献率降序排列，获取最前的k列数据形成矩阵W。

步骤5 利用矩阵W和样本集X进行矩阵的乘法得到降低到m维投影矩阵；

步骤6 将数据点权重置为0，重复步骤2、3、4，输出m维新矩阵。

1.3 DPCA-K-means 算法基本思想

为了消除各个特征在量纲化和数量级上的差别，对数据进行标准化，得到标准化矩阵。假设数据集中有n个数据点X={X1,X2,…,Xn}，被划分成k个分组{X1,X2,…,Xk}，k个质心C={c1,c2,…,ck}，要求k个分组满足以下条件：X1⋃X2⋃Xk=X；Ck∈Xk；Xi≠Φ，其中k=1,2,…,n。为消除量纲和尺度的影响[20]，首先将数据标准化，转化为无量纲的新数据集，便于不同单位或量级的指标能够进行比较和加权。标准化过程如式（3）：

式中：xij为第i个体系特征第j个样本的源数据；和σi分别是第i个特征体系的平均值和标准差。

根据标准化数据矩阵建立协方差矩阵，反映标准化后的数据之间相关关系密切程度的指标，其定义如式（4）：

式中：n代表数据点个数；Xi代表任意一个数据点；代表所有数据点的平均值。

样本均值计算方法如式（5）：

根据协方差矩阵R求出特征值、主成分贡献率和累计方差贡献率。求出特征值[21]λi(i=1,2,…,n)，按大小顺序排列，即λ1≥λ2≥…≥λi≥0。特征值是各主成分的方差，反映各个成分的影响力。把划分所占整个信息的权重定义如式（6），所有划分权重之和定义如式（7）：

式中：Wi表示每个特征在所有特征中所占的权重；W表示所有特征值的权重总和。

本研究中权重因子W的值为1，即累计特征值所占比例总和为100%，对数据重新进行加权处理后组成新的样本数据为。将权重因子乘以每个属性之后得到新的特征[22]，如式（8）：

欧氏距离[23]用来度量数据点与聚类中心之间的相似性。数据集X={X1,X2,…,Xn}的n个数据点，用m个元素值Xi={xi1,xi2,…,xim}组成该数据集的特征维度，特征组形成了m维空间，特征组中的每一个特征构成了每一维的数值。在m维空间下，2 个数据矩阵各形成了1 个点，计算这2 个点之间的距离，即为欧式距离。对其进行如下描述：

n个数据点X={X1,X2,…,Xn}，Xi={xi1,xi2,…,xim}中，其中2个数据Xi={xi1,xi2,…,xim} 和Xj={xj1,xj2,…,xjm}之间的距离D(XiXj)计算方法如式（9）：

式中：m表示数据点的特征维度。

第1个初始点选择最接近均值的数据点，记为C1；选择第2个初始点时，定义所有划分的均值点mi到第1个初始点C1的距离WDi。选择WDi最大的数据点为第2个初始聚类中心，记为C2。其中mi到第1个初始点C1的距离WDi，定义为加权欧几里德距离，如式（10）：

对于最小距离选择的描述如式（11）：

算法收敛条件为误差平和最小值，对提出的改进算法步骤描述如下：

步骤1执行DPCA 算法处理数据集进行重要度分析计算优胜特征的不同的权重，得到权重因子后对每个数据点求加权平均值；

步骤2根据加权平均值对数据进行整合排序，划分k个数据集；

步骤3计算每个数据集的平均值，取尽可能接近均值的数据点作为数据集的初始质心C1；

步骤4分别计算聚类中心Ci和数据集合中数据点Xi之间的加权欧式距离WDisti，继续选择其余质心；

步骤5将数据点分配给聚类最近的类中，在该聚类簇中数据点和聚类中心均有最小距离MinD，对于剩余样本数据，同样将其与距离最近的聚类中心归为一类；

步骤6计算每个类中所有对象的平均值作为新的聚类中心；

步骤7重复步骤5和步骤6，直到满足收敛条件。

改进算法流程如图1所示。

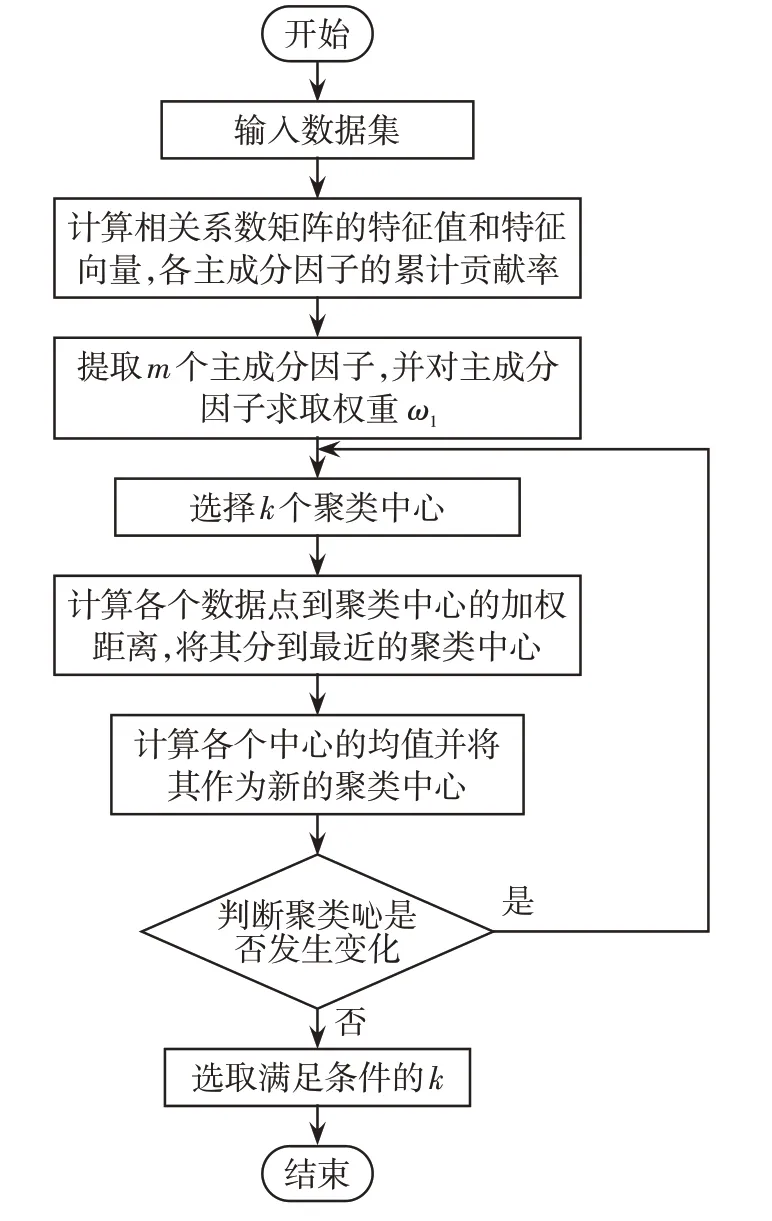
图1 DPCA-K-means 算法流程图Fig.1 Flow chart of DPCA-K-means

2 验证试验与结果分析

2.1 实验数据预处理

本研究原始数据包含学生的校园一卡通刷卡信息和成绩信息。数据清洗阶段，检测数据中是否存在“学院/专业”缺失的情况，如有则删除该条数据；是否存在不在食堂就餐的情况，如有则剔除该数据；清理刷卡消费价格为负数的异常点；检测数据中是否存在消费数据缺失的情况。实验之前将数据中行为习惯记录较少的记为异常点并进行剔除。

2.2 实验数据分析

实验通过PCA算法中处理的数据进行特征重要性分析得到每个特征的相对应的权重，如表1。

表1 特征权重表Tab.1 Feature weight table

对数据进行DPCA处理后取平均值，取尽可能近的均值作为每个子集的初始质心，选取对应平方误差和TSS最小值作为最优聚类结果。当最小值TSS=42.658 1的时候，迭代次数为7次，此时聚类结果最佳。

用户4个类别的聚类中心如表2、表3所示，可以明显看出各类学生之间的差别。

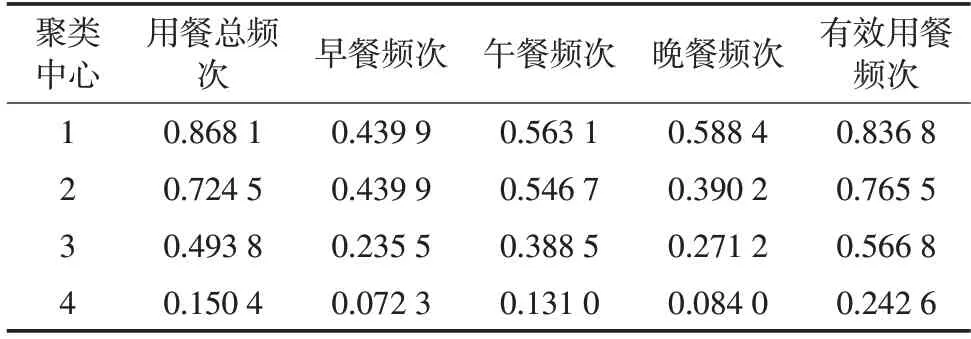
表2 聚类中心结果对比（1）Tab.2 Comparison of cluster center results（1）

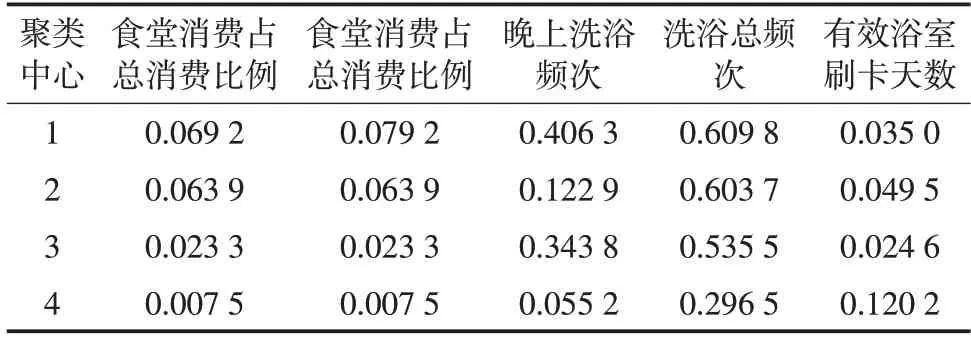
表3 聚类中心结果对比（2）Tab.3 Comparison of cluster center results（2）

学生用户画像实验结果分析如下：

学霸类型学生：此类学生上午洗浴频次和食堂消费占总消费比例均高于其余类别学生。他们吃早餐频率很高，并且习惯到食堂就餐，吃饭时间最为规律，整体校园生活习惯非常好，对应成绩在90分以上。

潜力类型学生：用餐总频次、学生吃早餐、食堂消费占总消费比例、食堂消费占总消费比例等特征低于学霸类型学生，但是高于另外两类学生。这类学生人群能够按时吃饭，在校行为生活习惯比较规律。与部分学霸类型学生的生活习惯非常相似，学习积极性相对较高，只是成绩上较低。若对此类型学生行为习惯重合的学生加以人为教导，他们的成绩将会有很大的提高，跻身学霸类型学生，对与学霸类学生行为不接近的学生进行人为调控，同样可以有进步，但是效果不如与学霸类学生人群重合的学生好。

普通类型学生：所有特征值比较均衡，可见此类学生中规中矩，去食堂的情况较正常，体现大多数学生的生活习惯，属于普通类型的学生。

不努力类型学生：数据显示各个特征聚类中心都小于其他类别学生，在食堂就餐频次很低，很少去食堂和浴室，生活习惯不规律，整体学习不够勤奋，学习状态较差。

为了能够直观的观察聚类的效果，选择影响最大的前3 个特征，聚类分析进行可视化展示。其中红色、绿色、蓝色、紫色分别代表聚类1、2、3、4，分别对应成绩大于90分，成绩在80～90分之间，成绩在60～80 分之间，成绩小于60 分4 类学生。PC1、PC2、PC3 分别代表加权后的有效用餐频次、学生早餐频次、食堂消费占总消费比例。通过图2可以清楚看到1、2类学生行为之间有重合，说明此类学生的行为习惯相似性很高，只是在成绩上稍微有差别，算法基本可以区分不同层次的学生。

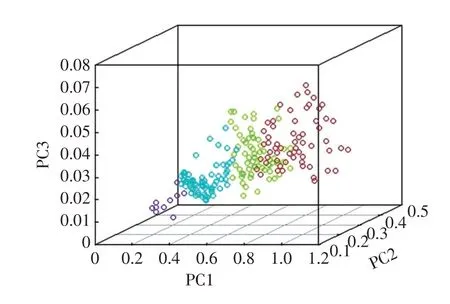
图2 重要特征三维聚类展示图Fig.2 3D cluster display of important features

将数据进行融合后得到训练集聚类可视化展示，计算数据点到聚类中心的距离，如图3所示。其中横轴代表聚类簇，纵轴代表数据点到质心的距离，图例分别表示各个类别。

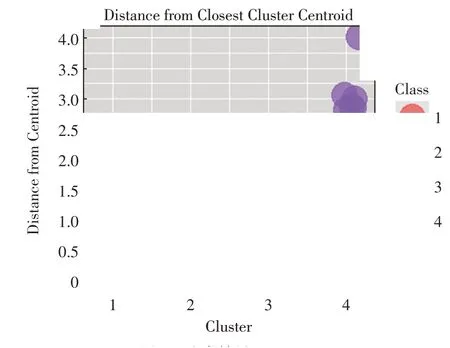
图3 聚类结果展示Fig.3 Comparison of cable tension under different magnitudes

为了检验本研究所提出的DPCA-K-means 算法的有效性，采用传统PCA 结合K-means 算法的PCA-KMeans 和随机选择初始聚类中心的传统基于欧几里得距离的Euclidean-K-means算法作对比实验分别对数据进行聚类，得到准确率的结果，如表4。

表4 不同聚类方法验证性对比Tab.4 Verification comparison of different clustering methods

可以看出DPCA-K-means 算法通过特征多样性的选取并通过权重调整聚类中心选择，聚类的准确率较传统方法有着显著的提高[24]，对于学生用户画像起到了明显作用。

3 结语

通过分析校园一卡通中学生的行为习惯，DPCAK-means 算法采用特征选择和特征加权方式对数据进行聚类分析将学生划分为成绩好行为规律且早起的学霸类型、成绩较好行为规律的潜力类型、成绩一般行为不太规律的普通类型和很少早起且生活不规律的不努力类型。通过对比试验可以看出该算法的准确率最高，可见此算法改进对分析学生行为有实用性。但由于一卡通数据的有限性，其数据不包含学生进出宿舍的数据，因此未能深入分析此因素对于成绩的影响。接下来的分析将在此基础上进行突破，并增强数据的适应性功能。