铁磁形状记忆合金(FSMA)智能复合材料力学性能仿真与探讨

卞兴宇，薛立军

(1.天津市先进机电系统设计与智能控制重点实验室，天津 300384； 2.天津理工大学 机械工程学院/机电工程国家级实验教学示范中心，天津 300384)

1 前 言

铁磁形状记忆合金(FSMA)是上世纪末发展起来的一种新型智能材料。与传统的形状记忆材料、磁致伸缩材料和智能高分子材料相比，FSMA兼具温控和磁控的特性，且比一般材料的响应速度快，输出应变大。随后相关研究人员提出了将FSMA颗粒与树脂混合制备出智能复合材料的概念，这种想法引起了学术界的广泛讨论。文献[1]首先提出了Ni2MnGa颗粒/树脂智能复合材料这一概念，并在制备相关试件后对其基本力学性能进行了研究。

近年来的研究主要针对FSMA复合智能材料的制备、相变特性、力学性能等方面，对其力学性能方面的研究还不全面。本研究使用有限元分析软件对Ni50Mn28Ga22合金与环氧树脂组成的智能复合材料的力学行为进行有限元分析和数值模拟，考虑颗粒含量、磁场、预应力及不完全加卸载等对复合材料性能的影响，并与实验值进行对比。

2 Ni2MnGa智能复合材料模型建立

2.1 FSMA本构方程

类比于形状记忆合金的应变，在小变形情况下，当施加一个垂直于横向磁场的压应力时，FSMA的总应变可表示为：

ε=εe+εtr+εα

(1)

式中，εe为弹性应变，εtr为重取向应变,εα为热应变。由于马氏体重取向过程中未发生马氏体相到奥氏体相的转变，令ξσ表示应力择优马氏体含量，则磁场择优马氏体含量ξH表示为：

ξH=1-ξσ

(2)

假设最大的重取向应变为εL，初始应变为0，当材料完全由磁场择优马氏体转化为应力择优马氏体时，根据文献[2]可知：

εtr=ξσεL

(3)

又因为热应变比重取向应变小几个数量级[3]，所以一般研究中可忽略εα的影响。FSMA杨氏模量E的大小与马氏体变体含量有关，基于文献[3]，可以表示为应力择优马氏体含量的函数：

E=E(ξσ)=ξσEσ+(1-ξσ)EH

(4)

式中：Eσ和EH为应力择优马氏体和磁场择优马氏体的杨氏模量。所以总的应力应变关系为：

σ=(ξσEσ+(1-ξσ)EH)(ε-εLξσ)

(5)

描述马氏体相变的表达式较少，本研究引用文献[4]的双曲正切函数来描述马氏体变体的重取向含量：

(6)

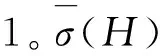
从表1可以看出，甘啤5号、垦啤7号、甘啤3号出苗较晚，比其他品种晚1 d；甘啤5号、垦啤6号、甘啤4号的抽穗期较早，均为6月9日，而其余品种的抽穗期为6月10日；博乐、垦啤6号、玛俐、甘啤3号均为早熟品种，而甘啤5号成熟最晚，较对照晚7d。从全生育期来看，甘啤5号生育期最长，垦啤7号、甘啤3号、甘啤4号、甘啤6号的生育期适中。

2.2 FSMA复合材料本构方程

在研究复合材料细观力学的方法中，联合使用Eshelby原理和Mori-Tanaka场平均法相对较多。本研究基于马氏体重取向的行为，建立了以环氧树脂为基体，Ni2MnGa合金为球形颗粒夹杂的复合材料本构理论模型。假设环氧树脂和Ni2MnGa颗粒为各向同性线弹性材料，并且开始时合金完全处于应力择优马氏体状态，那么在远场力σ0作用下基体产生的形变为ε0。当基体内某部分被同等大小的合金颗粒替代时，颗粒与基体之间相互作用产生的扰动应力与应变分别记为σpt和εpt，所以基体应力σ0可表示为：

σ0=L0(ε0+εpt)

(7)

式中：颗粒的平均应力应变与基体的平均应力应变之差记为σ′和ε′，根据Eshelby理论，合金颗粒的应力σ1等效方程为：

σ1=L1(ε0+εpt+ε′)=L0(ε0+εpt+ε′-ε*)

(8)

式中：ε*为本征应变，且

ε′=Sε*

(9)

式中：S为四阶Eshelby张量，其取值仅依赖于基体材料刚度和颗粒的方向、形状。当颗粒为球状时，S张量为常量，有：

(10)

式中：v0为基体的泊松比。设ξ0为基体的体积分数，则合金颗粒体积分数ξ1为：

ξ1=1-ξ0

(11)

(12)

则扰动应力应变可表示为：

(13)

进一步得到本征应变为：

(14)

{-(L1-L0)[S(1-ξ1)+Iξ1]-L0}=Z

(15)

所以基体的平均应力最终表示为：

σ0=L0(ε0+εpt)=L0[ε0-ξ1(S-I)ε*]

(16)

复合材料的平均应变为：

=[1+ξ1Z-1(L1-L0)](L0)-1σ0

(17)

式中：[1+ξ1Z-1(L1-L0)]-1(L0)为等效刚度矩阵，其与颗粒材料的含量、形状、弹性模量及基体材料的弹性模量、泊松比等有关。当合金颗粒的体积分数已知时，根据此式可计算出材料在发生重取向过程中随外磁场、外应力的变化情况。

2.3 FSMA复合材料有限元建模

在进行有限元分析时，对整个材料进行模拟相对复杂，因此简化并抽象成一个有代表性的模型非常必要。所以，在假定均匀和周期性结构的情况下，通常采用晶胞作为代表模型来研究两相材料的力学行为。根据Ni-Mn-Ga合金颗粒/树脂智能复合材料特性，提出以环氧树脂基体(E-51)包裹合金颗粒(Ni-Mn-Ga)的设计方案，建立的三维单元有限元模型如图1所示。首先建立了由球形粒子随机排列于基体中的智能复合材料的一般模型，如图1(a)所示。在假定各向同性和均匀复合材料的情况下，忽略邻近单胞的影响，并将其简化为图1(b)所示的单个合金粒子嵌入树脂基体中的单元模型。此外，由于所建立的模型是中心对称的，本研究将单元模型的八分之一作为计算模型，以节省计算时间(图1(c))。在该计算模型中，合金颗粒和树脂基体的材料参数如表1所示。为了分析合金粒子含量对智能复合材料的影响，建立了含量分别为10%，20%，30%的分析模型。其中球形颗粒的半径为0.0225 mm，立方细胞模型的棱长分别为0.078，0.062和0.054 mm。

表1 材料相关力学参数Table 1 Mechanical parameters of the material

图2为所构建的模型之一(棱长为0.0225 mm，体积分数为20%的1/8模型)，其余模型与此模型类似。对模型进行网格划分时，在合金颗粒/树脂分界边缘附近制作了更精细的网格，此举可使有限元结果更精确。在保证计算精度的前提下，将远离分界边缘的网格精度设置为中等，加速收敛时间，最后所得模型单元数为8656，节点数为15321。

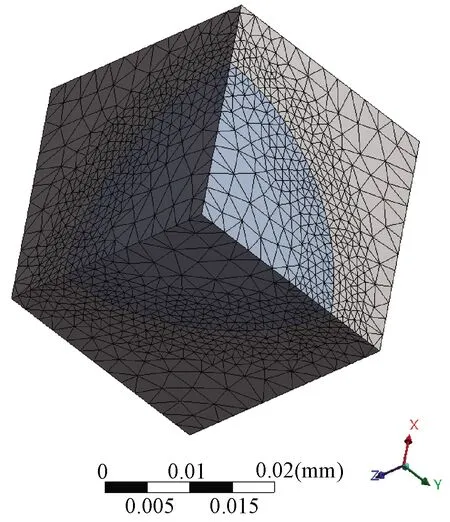
图2 20%体积含量模型网格划分Fig. 2 20% volume content model meshing

在有限元建模时，施加周期性边界条件控制三个对称面上的法向位移为0，加载面在加载时相对于其原始形状不变，保持直线和平行移动。保证了相邻单胞的变形情况，即满足代表性模型要求。

根据文献[6-7]得到Ni50Mn28Ga22的各个相变点温度分别为Ms=301.29 K，Mf=292.83 K，As=306.77 K和Af=316.55 K，居里温度为366.8 K。同时，常温下热膨胀系数为20×10-6/K，温度系数为0.003 K。

3 力学性能分析

3.1 马氏体重取向过程的理论模型验证

FSMA初始为磁场择优马氏体构成，在分析时施加一个垂直于横向磁场的压应力。根据文献[2]已有材料数据计算出的相关参数见表2。利用MATLAB软件对重取向过程进行数值分析。

表2 重取向过程材料参数Table 2 Mechanical parameters of the material

不同的磁场下，FSMA的应力择优马氏体变体含量随压应力的变化情况见图3。从图可见，应力择优变体含量随压应力的增加而增加，最终完全转化为应力择优变体时达到饱和状态。随着磁场的增加，马氏体重取向开始时应力也会有所增加。卸载时，应力择优马氏体重新转化为磁场择优马氏体，最终完全转化为磁场择优马氏体。

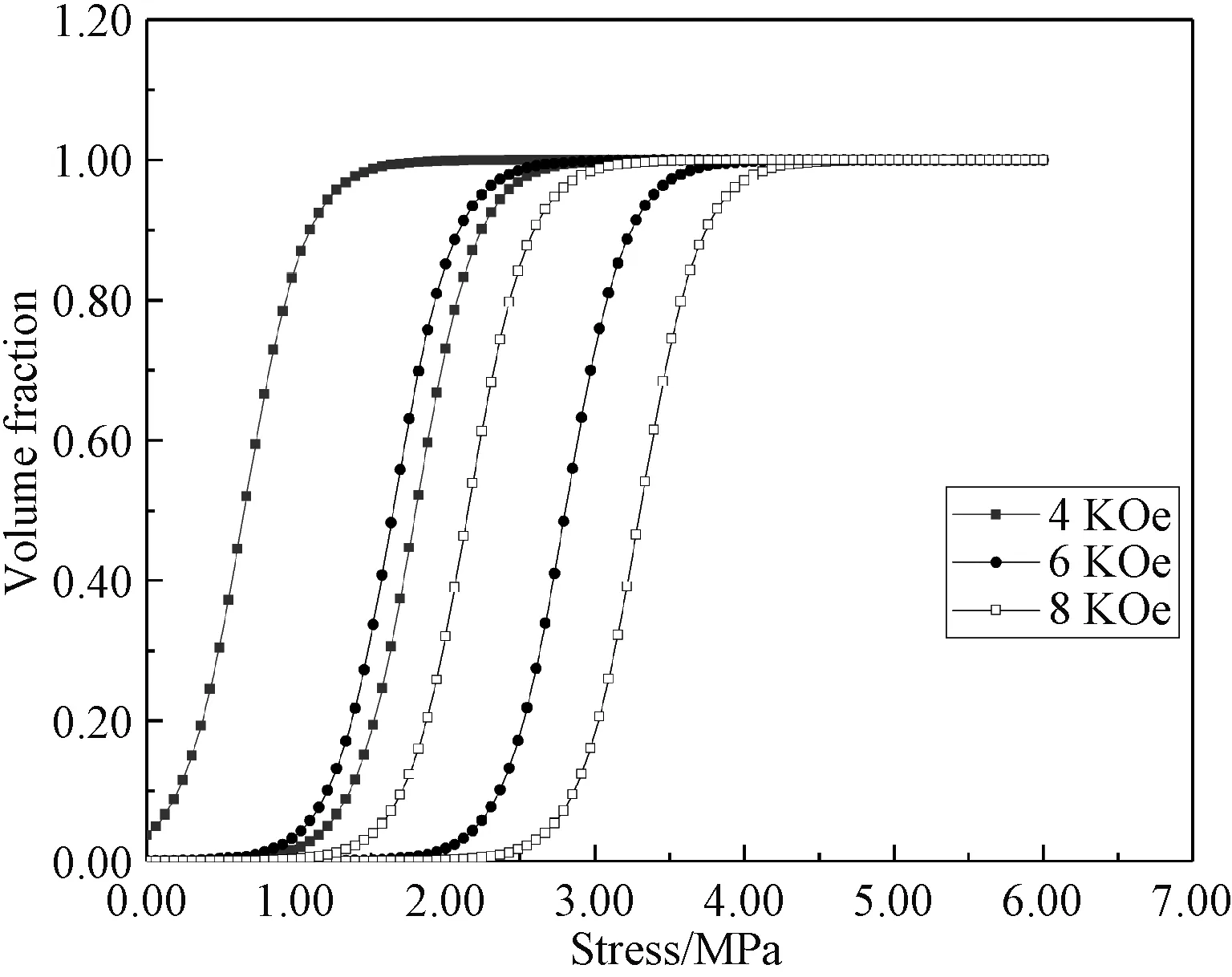
图3 应力择优变体随压应力变化曲线Fig. 3 Stress preferred variant varies with stress

图4显示了在6 KOe的磁场下，FSMA的应力-应变曲线，并将MATLAB的结果与文献[4]对照。从图可见，模拟总体变化情况于形状记忆合金类似。在未发生马氏体变体转变时，应力-应变曲线呈线性；当马氏体变体随压力的增加而开始转变时，应变在一个较小的应力范围内迅速增加；当变体转化完全时，应力-应变曲线又变成线性。在卸载时，马氏体变体又从完全应力择优变体开始向磁场择优变体转化，其应力-应变曲线与加载相反。

图4 磁场强度为6 KOe时的应力-应变曲线Fig. 4 Stress-strain curve when the magnetic field at 6 KOe

3.2 复合材料模型验证

假设材料受到一定的预压力，初始全为应力择优的马氏体相，模拟复合材料在磁场诱发下的马氏体重取向行为。图5显示了在不同的预压力作用下，复合材料中Ni2MnGa颗粒的弹性模量随磁场的变化情况。因为应力择优变体的弹性模量高于磁场择优变体，在增加磁场后，即马氏体变体由应力择优转化为磁场择优时，颗粒的弹性模量降低。并且在预压力较大时，应力择优马氏体转变不完全，最后为应力择优与磁场择优马氏体共存，所以弹性模量较大。

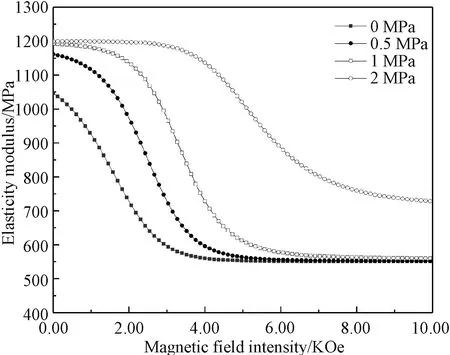
图5 弹性模量随磁场变化曲线Fig. 5 Curve of elastic modulus with magnetic field

在无外力作用时，不同含量的FSMA复合材料的应变磁场强度曲线见图6。从图可见，复合材料的应变完全由磁场产生，且随磁场增加，会逐渐达到一个饱和值。当颗粒含量越高时，产生的磁致应变越大，复合材料能达到的饱和平均应变就越高。

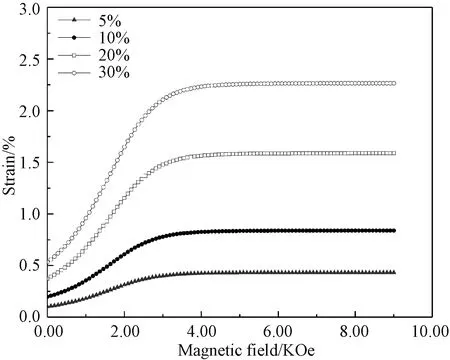
图6 复合材料平均应变与磁场关系Fig. 6 Relationship between average strain and magnetic field in composites

图7为复合材料的等效弹性模量和球形颗粒含量的关系。假设颗粒的弹性模量不随磁场发生改变，设Ni2MnGa的弹性模量为11.25 GPa[11]。当颗粒含量增加时，复合材料的等效弹性模量也随之非线性增加。当材料全部为基体时，等效弹性模量是基体的弹性模量为3.134 GPa；当材料全部由铁磁颗粒组成，颗粒复合材料的等效弹性模量达到最大为11.25 GPa。

图7 复合材料弹性模量与颗粒含量关系Fig. 7 Relationship between elastic modulus and particle content of composite materials

3.3 力与温度耦合

模拟FSMA在不同温度下的单轴压缩实验。在不同温度对材料施加一个同等大小的单轴应力。如图8所示，当温度为320 K和318 K时(高于奥氏体结束温度Af)，材料显示了伪弹性：其应力-应变曲线在未达到应力极限时呈线性，直到应力分别加载到130和118 MPa时，诱发了马氏体相变，类似于屈服阶段，导致材料的硬度降低。随着压力的进一步增加，材料完全由奥氏体转变为马氏体，应变达到最大。当应力超过弹性极限后，随应力缓慢增加，应变迅速增加。在一定的应变范围内卸载时，高温下相对不不稳定的马氏体变体会先回复到一个缓慢变化阶段，此阶段的应力水平较低于正向转变，此时的变化过程称为马氏体逆相变。随着应力减小到0，应变也完全消失。当环境温度为310 K时(介于奥氏体开始As与结束温度Af)，发生相变的应力点低于在温度大于Af的应力点，即正向应变发生较早，反向应变发生较迟，最终在完全卸载后应变未完全释放，产生残余应变。当温度为305 K时(低于奥氏体开始温度As)，正向转变发生在更低的温度，且卸载阶段都未发生转变，产生更大的残余应变。此模拟与实验得出的结论相同，验证了本模型的可靠性。

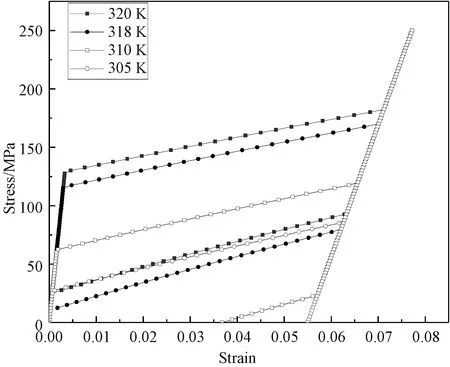
图8 FSMA的压缩应力-应变曲线Fig. 8 FSMA compressive stress-strain curve

在引入环氧树脂模型后，对材料施加同样的边界条件和外载荷时，得到的压缩应力应变如图9所示。环氧树脂引入后得到的复合材料在单轴载荷下与MSMA的变化趋势一致，这与Hosoda等[1]的研究结果相同。但是相对于FSMA而言，复合材料发生马氏体相变的应力明显降低，且增大了马氏体相变点的应变值，即树脂基体承受了较大载荷。在继续加载使产生马氏体相变至马氏体相变完成时，所需载荷更大，且转变完成时应变较小。在卸载阶段，当温度低于As时，发生了反向转变，且产生的残余应变更小。由图10a可知，在单轴应力作用下，复合材料中较大的变形集中在基体中，合金部分的变形较小，还有一小部分未发生变形；由图10b和图10c的应力应变分布云图可知，颗粒与基体交界面处的应力较小，在远离界面时应力增大；颗粒的应变比基体的应变小一个数量级。

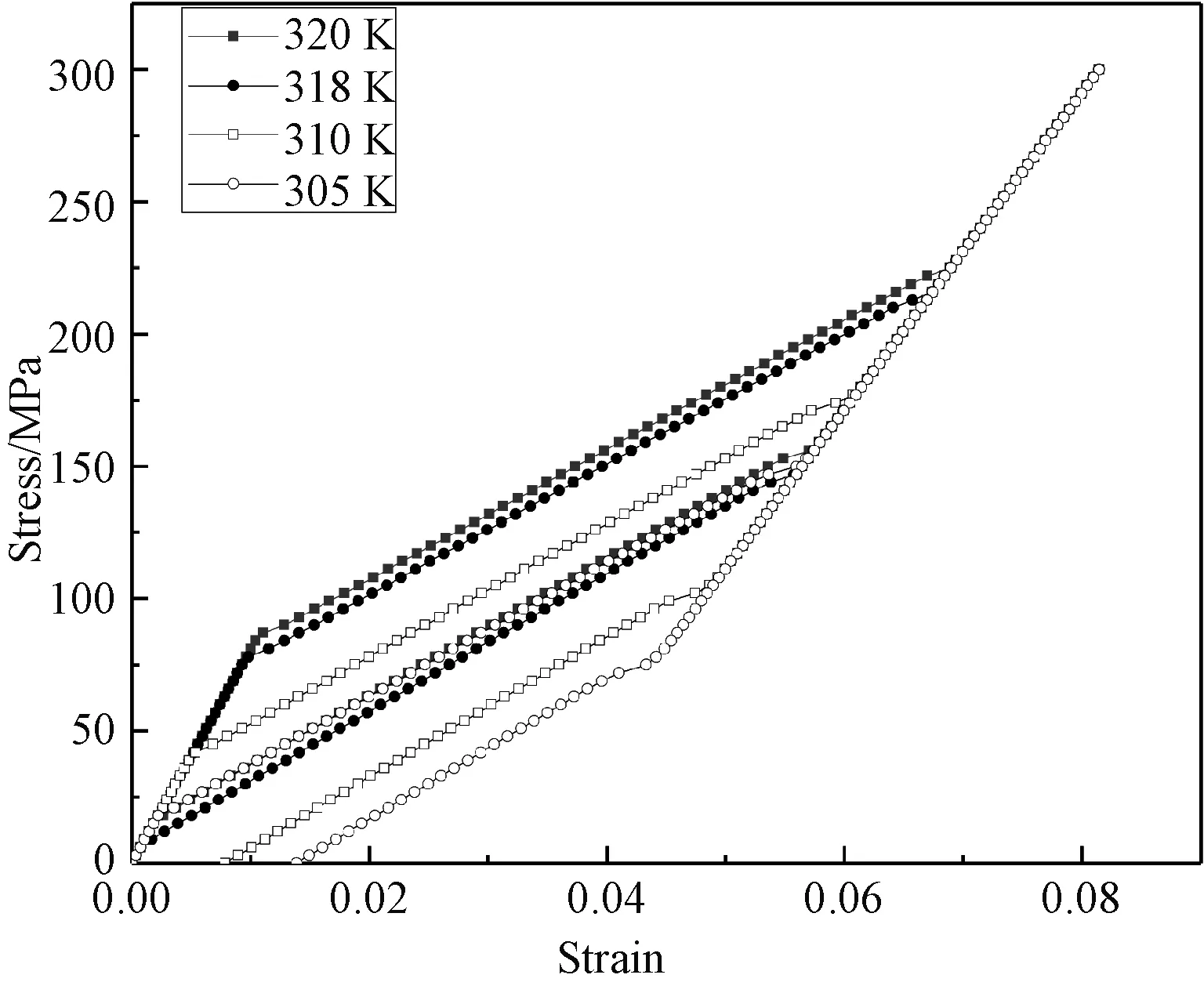
图9 10%体积含量复合材料的压缩应力应变Fig. 9 Compression stress-strain of 10% volume content composite material

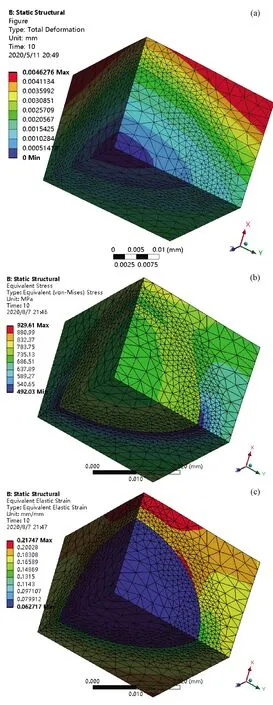
图10 20%体积含量复合材料的(a)总位移图；(b)应力图；(c)应变图Fig. 10 20% volume content composite material (a)total displacement; (b)stress; (c)strain

在增加Ni50Mn28Ga22体积分数后，得到的压缩应力应变如图11所示。对比图9可知，20%含量的复合材料在加载过程中发生正向转变的临界应变较小，在发生马氏体相变阶段，同样的应力产生的应变较小。在卸载阶段中发生逆相转变的临界应力较小，且在温度低于Af时，产生的残余应变较大。

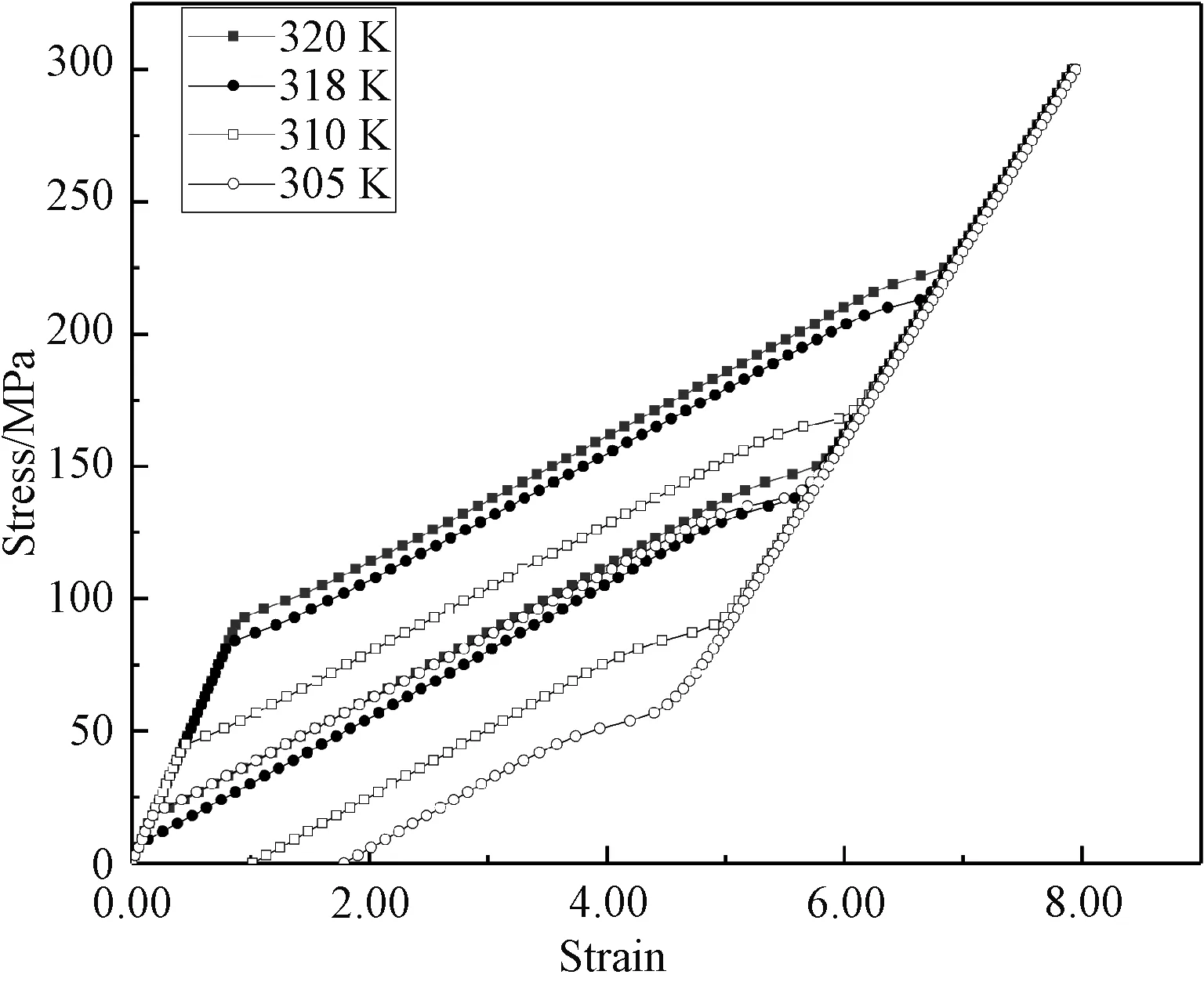
图11 20%体积含量复合材料的压缩应力应变Fig. 11 Compression stress-strain of 20% volume content composite material

3.4 Ni2MnGa合金/树脂复合材料形状记忆效应

Ni2MnGa合金包含铁磁性和热弹性马氏体相变特征，即在温度场、力场和磁场作用下产生对应外场诱发的马氏体变体。在外加磁场作用下Ni2MnGa合金外界输出应变包含磁致伸缩应变和由马氏体变体孪晶再取向产生的应变，但两者产生的应变大小区别过大，因此其应变主要为马氏体变体孪晶再取向产生的应变。此应变能通过加热或去掉磁场恢复，使材料完全恢复其初始状态，且该效应也具有滞后性和可逆性。图12为20%含量的复合材料模拟形状记忆效应。材料先在305 K下经过一轮加载卸载使其产生残余应变，再升温至320 K，发现残余应变完全消失，恢复应变在1.8%左右。

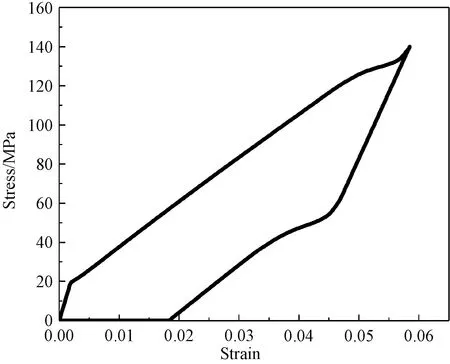
图12 20%体积含量复合材料形状记忆效应Fig. 12 Shape memory effect of 20% volume content composite material

3.5 不完全循环加卸载

图13显示了在不完全循环加卸载时，应力-应变曲线和马氏体体积分数的变化情况。从图13(a)可见，当第一次加载至应变为0.065时，对应着图13(b)马氏体体积分数到达1，即材料完全变为马氏体。继续加载，应变随应力增大，马氏体体积分数保持不变。当第一次卸载到应变为0.026时，材料再次加载，此时马氏体体积分数短暂停止后重新增加。当加载到应变为0.052时材料再次卸载，应力降低，最后应力减小到零，马氏体又再次重新转换为奥氏体。从图13(a)可见，当第二次进行加载卸载后，应力-应变曲线高于第一次加载的曲线，低于第一次卸载的曲线，即基体蠕变使材料产生同等大小的应变时所需应力增大。

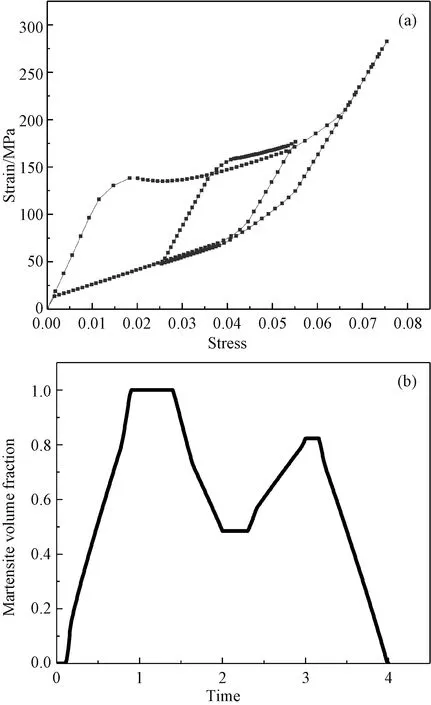
图13 不完全加卸载时的应力-应变曲线(a)和(b)马氏体体积分数Fig. 13 (a)Incomplete loading and unloading (b)Martensite volume fraction

4 结 论

本研究基于FAMA本构模型，结合Eshelby理论和Mori-Tanaka场平均方法，建立了FAMA智能复合材料的本构模型。利用此模型分析了在马氏体重取向过程中FAMA的体积含量，外场等因素对复合材料性弹性性能的影响；分析了在马氏体相变过程中不同温度对应力应变产生的影响。

在压缩载荷作用下，材料的变形大部分发生在复合材料中的基体部分。且相较其他方向，沿加载方向存在着一个较大的应变区域，促进了颗粒附近孔隙的形成。随着Ni2MnGa颗粒含量的增加，同等条件下卸载后产生的残余应变更大；随着温度的升高，应变所需的应力更大。

随后对复合材料的形状记忆效应和不完全加卸载的马氏体体积分数变化情况进行了模拟仿真，结果表明复合材料能较好的保证材料的原始性能，且在一定程度上弥补了原材料的不足。但是本研究在建模过程为了方便和简化对模型采用了一些假设，并且只研究了稳态下的力学性能。因此为了完善材料的相关性能，还需要对其进行进一步的探讨。